基于神经元的方波发生器设计及参数优化

张明亮，徐新阳，杨新梦，刘丽茹

1.陆军工程大学石家庄校区电磁环境效应重点实验室，河北石家庄 050003；2.石家庄铁道大学机械工程学院，河北石家庄 050043；3.兰州交通大学光电技术与智能控制教育部重点实验室，甘肃兰州 730070

前言

神经系统是生物的重要组成部分之一，对生理活动起着重要的调控作用［1］。神经系统由数以万亿计的神经元组成，这些神经元具有传递和处理复杂信号的功能，且在信息传递处理时表现出很强的抗干扰能力。由于电子设备的智能化程度不断提高，电路中的电子元件越来越多，集成度越来越高。但随之而来的是电路工作时有意无意向外辐射和传导电磁场，使得自身和其它电子元件受到影响，需要对电子设备进行电磁防护。传统的电磁防护方法已经取得了较好的防护效果，但随着电磁环境日益复杂，传统方法不能满足防护的全部要求。针对电磁防护的现状，中国工程院刘尚合院士在2002年以生物抗干扰现象和行为为启发提出了电磁防护仿生的概念，利用生物本身对电磁干扰的防护和自我修复能力实现电磁防护的目的［2］。电磁防护仿生的理论基础是生物的抗干扰机制，尤其是神经元的抗干扰机制。为了揭示神经元的抗干扰机制，需要对神经元的动力学特性进行研究。

在20 世纪50年代，Hodgkin 和Huxley 两位学者首次提出描述神经元的数学模型，即Hodgkin-Huxley（HH）模型，该模型是最接近生物机理的神经元模型［3］。2015年，郭磊等［4］通过磁刺激脑部穴位获得了脑电信号，以此构建了脑功能网络，并对脑功能网络进行分析，发现信息传递速度在磁刺激下增强的现象。2017年，闻佳等［5］运用FPGA 实现了基于HH 模型的神经网络硬件仿真，验证了硬件仿真模型结果的正确性。2018年，易飞鸿等［6］通过数值模拟的方法分析了HH 模型各个离子通道反电动势参数对动作电位的影响。2019年，徐桂芝等［7］运用经颅磁刺激技术进行相关研究，研究表明经颅磁刺激技术在治疗神经性疾病具有显著的作用。

为了更好地利用神经元的抗干扰机制，本研究提出基于神经元的方波发生器。利用Simulink 搭建神经元仿真分析程序，在神经元仿真分析程序的基础上搭建基于神经元的方波发生器实现程序，利用Minitab 软件设计田口试验方案，对方波发生器的影响参数进行研究，分析模型参数影响占空比的程度，得到最优组合参数方案。

1 基于HH模型的方波发生器建模

在众多神经元数学模型中，HH 模型中的参数与电路参数比较接近，且具有含义明确的等效电路特征，易与仿生原型电路结合，故本研究重点对HH 模型进行分析。

1.1 HH模型

HH模型的数学表达式［3］如下所示：

其中，C表示神经元膜电容，V表示神经元膜电位，GNa表示钠离子通道最大导电率，m表示钠离子通道激活参数，h表示钠离子通道不激活参数，ENa表示钠离子通道反电动势，GK表示钾离子通道最大导电率，n表示钾离子通道激活参数，EK表示钾离子通道反电动势，GL表示漏电流电导，EL表示漏电流反电动势，I表示外界刺激电流，α和β函数是与神经元膜电位有关的速率常数，α函数和β函数表达式如下所述：

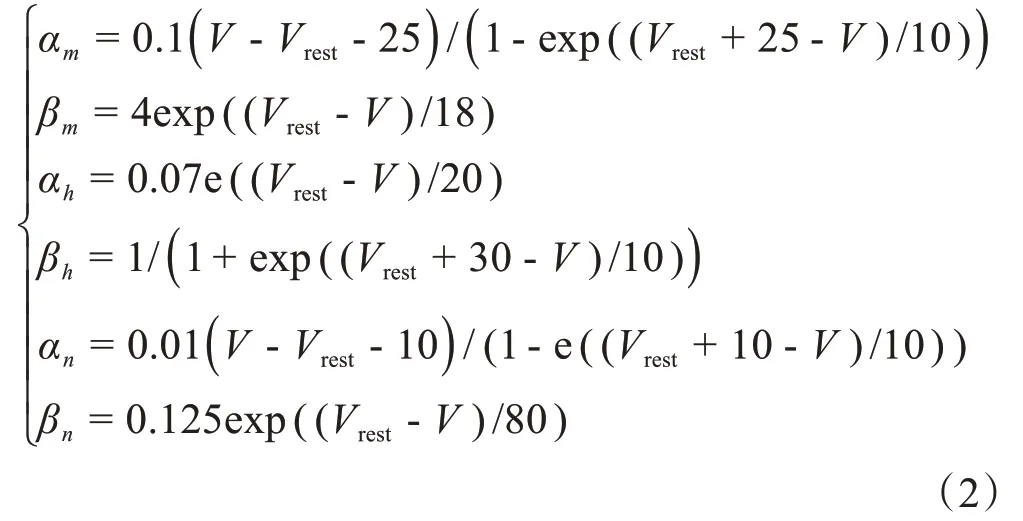
1.2 HH模型仿真程序搭建

HH 模型是由4个一阶微分方程组式（1）组成，该方程具有非线性和耦合特性，解析求解十分困难。为了得到特定条件下的时频形影，需要对其进行数值求解。为了方便数值求解，本研究利用Simulink工具箱搭建了用于计算HH 模型的仿真程序，如图1所示。

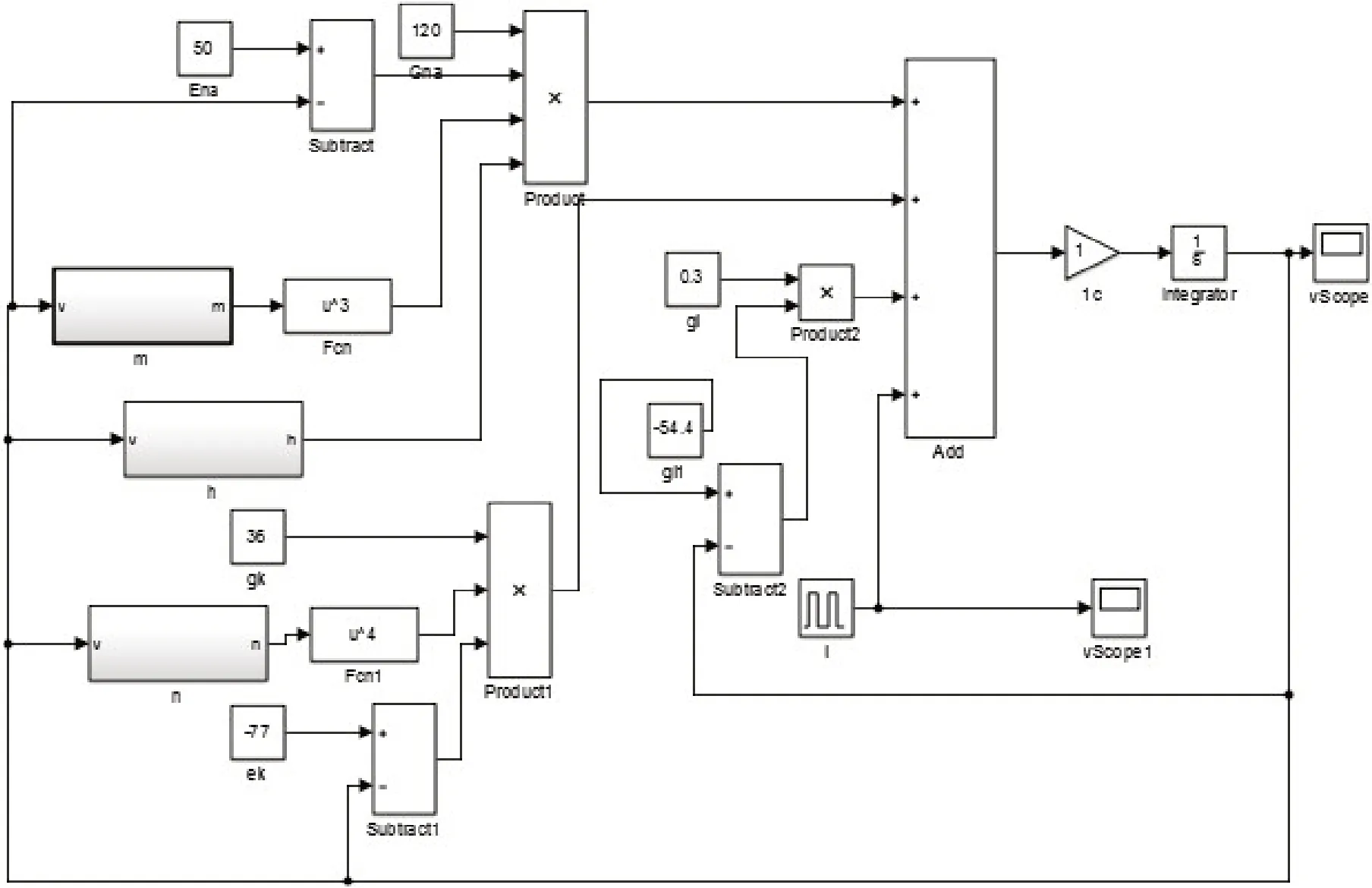
图1 HH模型整体程序图Figure 1 The whole program of Hodgkin-Huxley(HH)model

根据式（1）和式（2），可得到h、m、n参数实现的子模块，如图2～图4所示。

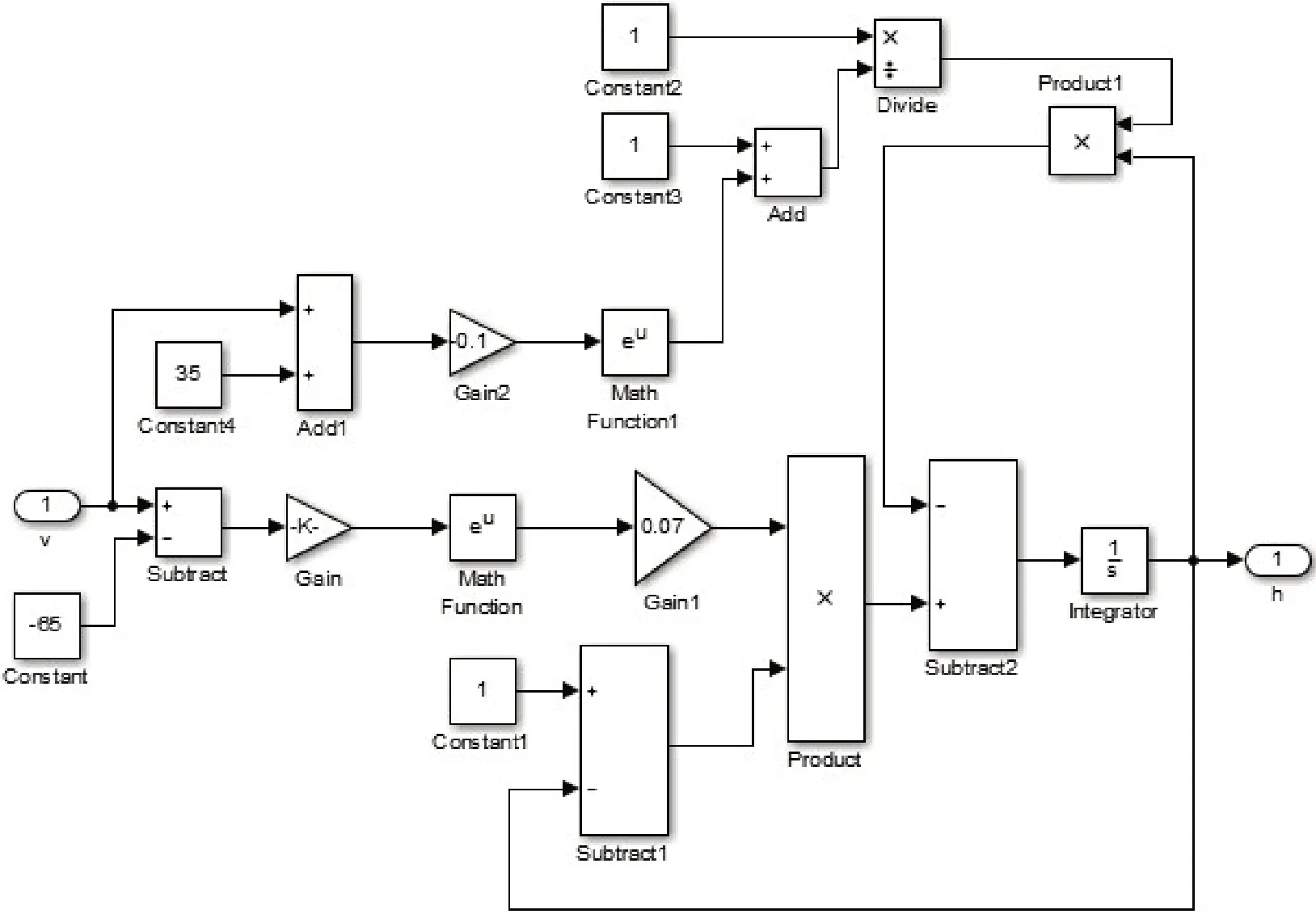
图2 参数h程序模块Figure 2 Parameter h program module

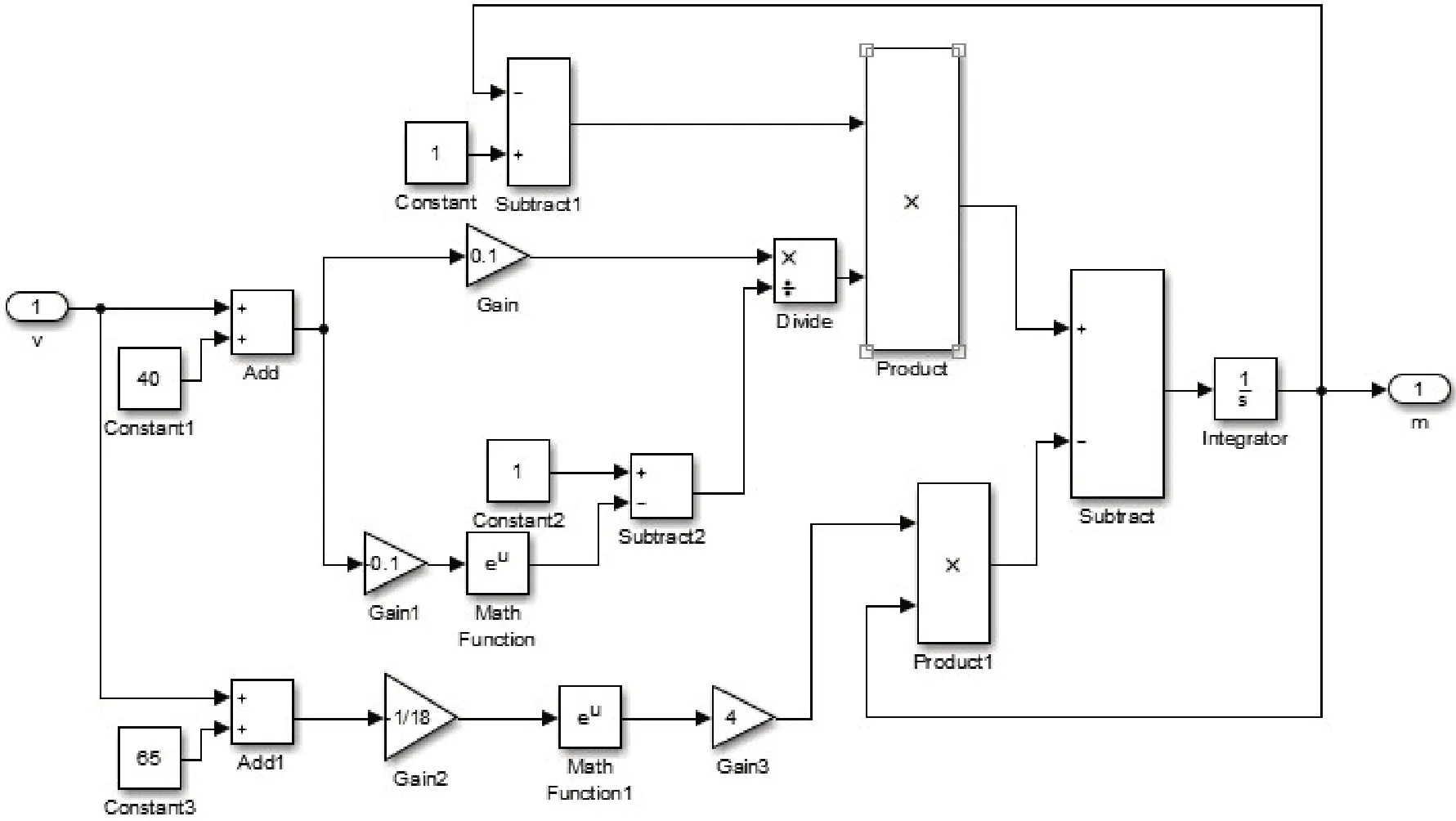
图3 参数m程序模块Figure 3 Parameter m program module

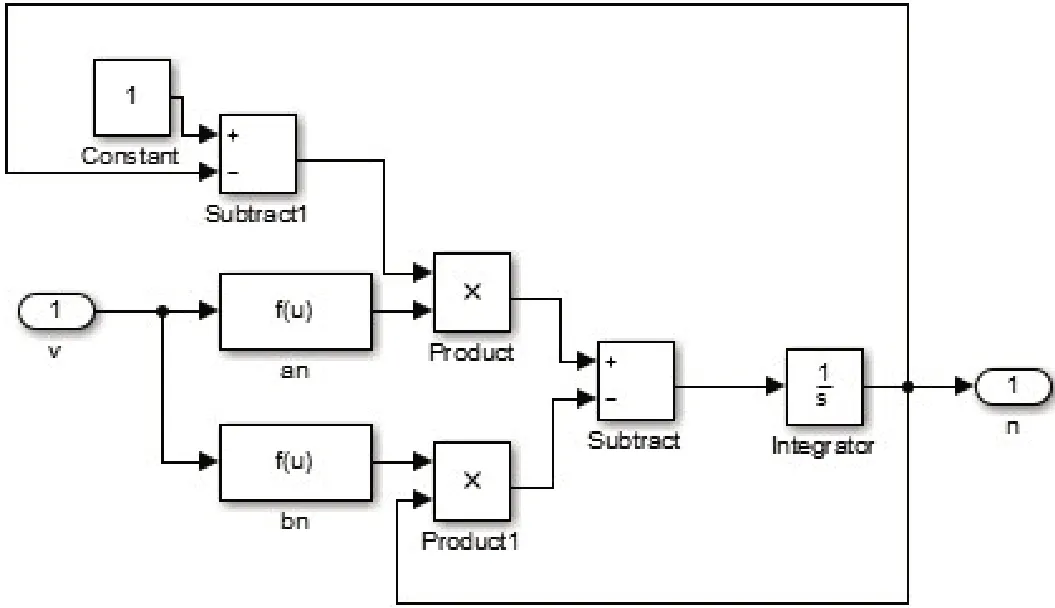
图4 参数n程序模块Figure 4 Parameter n program module

为了能够得到V的解，需对HH 模型中的各个参数进行赋值，仿真参数见表1。

1.3 基于神经元的方波发生器实现程序搭建

方波信号被广泛用作通讯、雷达、计算机及其它电子设备的信号源。由于神经元具有抗干扰特性，本研究以HH 模型为基础提出基于神经元的方波发生器，可以为电子信息和人工智能设备提供稳定抗干扰的信号源。在图1 的基础上利用Simulink 工具箱搭建新型方波发生器的实现程序，如图5所示。

方波发生器程序较HH 模型程序而言，程序中加入了Switch 模块，该模块的功能是用常数去截取动作电位。设置方波的高电平为5，低电平为0。当动作电位大于截取常数值时，输出高电平5；当动作电位小于截取常数值时，输出低电平0。假定外界刺激的幅值为50 μA/cm2，周期10，占空比20，截取参数为30 mV时仿真结果见表2。由表2数据可以观察到方波波形在初始阶段会有较大的波动，即方波的占空比和周期在开始的一段时间内不稳定。随着仿真时间的增加，在第3 个、第4 个波形后，占空比和周期趋于稳定值。计算两个相邻波形的周期差（即后一个波形周期减去前一个波形周期）为：-0.247 2、-0.008 2、0.000 4、0.000 1、0、0、0、0、0，从周期差可以看出波形周期差值绝对值逐步趋于0，周期从第4 组开始趋于稳定，并保持为10；同理，对相邻两个方波占空比做差，差值为-0.988 1、-0.071 5、0.000 8、0、0、0、0、0、0，占空比差值也逐步趋于0，并从第5 个波形开始占空比趋于定值。为了波形稳定，本研究采用第10 个波形作为标准，因为此时的周期和占空比已经比较稳定。

由于设置不同的截取常数，可以得到不同占空比的方波信号。本研究取30、0、-15、-25、-30、-35 mV为截取常数，研究截取常数对方波发生器占空比的影响。不同截取常数时第10个波形的仿真结果见表3。由表3可以观察到以-35 mV作为截取常数时具有较大的占空比，波形的上升沿时间更小，故以这时截取的常数为截取标准，研究HH 模型中不同参数（各离子通道的电导和反电动势）对占空比的影响。

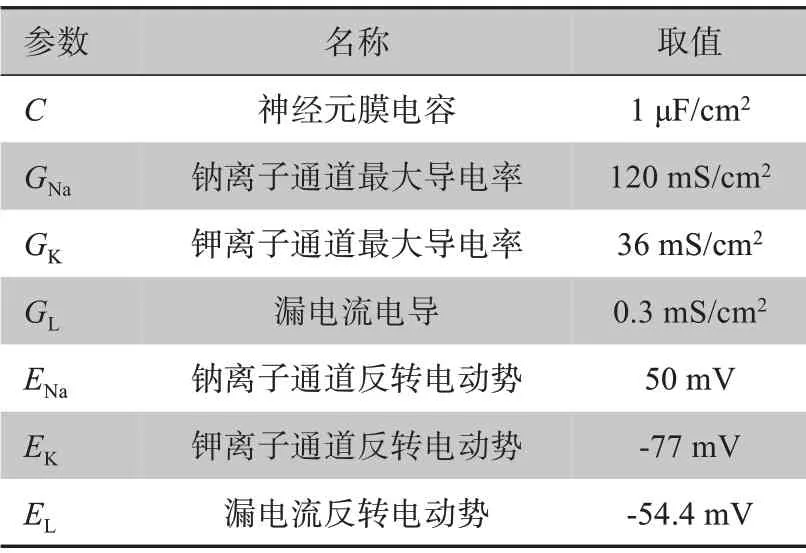
表1 HH模型中的各参数取值Table 1 Value of each parameter in HH model

由以上仿真结果可知，基于神经元的方波发生器具有一定的自我调节功能，方波的占空比和周期逐渐趋于稳定。

2 基于田口法的参数优化

基于神经元的方波发生器可以作为其它电子设备的外部输入信号。现阶段，我国在磁悬浮列车方面取得了较大进展，磁悬浮列车的关键组成部分之一是悬浮斩波器［8-13］。悬浮斩波器作为控制执行单元，通过把悬浮间隙位移、加速度等信号转换为数字信号，对这些数字信号计算值与预设值进行比较，根据对比结果反馈到中央控制器，向悬浮斩波器发出控制指令，保证列车的正常行驶。中央控制器发出控制指令实质是通过脉冲激励信号不同占空比控制悬浮斩波器内部相关开关器件开闭时间占比，从而改变电磁铁的电流大小［14-18］。因此本研究以磁悬浮列车斩波器需要的方波信号要求为例进行分析。基于神经元的方波发生器可为悬浮斩波器的内部开关器件提供脉冲激励信号。由于悬浮斩波器脉冲激励的特殊性（占空比大于50%才能稳定悬浮），而基于神经元的方波发生器占空比小于50%，故将方波发生器的反相波形作为脉冲激励，即低电平变为高电平，高电平变为低电平。由此可知，田口试验的期望特性要求方波发生器产生的方波波形的占空比越小越好。为了得到更小占空比的方波波形，接下来将利用田口法对方波发生器的影响参数进行优化。

图5 基于神经元的方波发生器程序图Figure 5 Program chart of square wave generator based on neurons

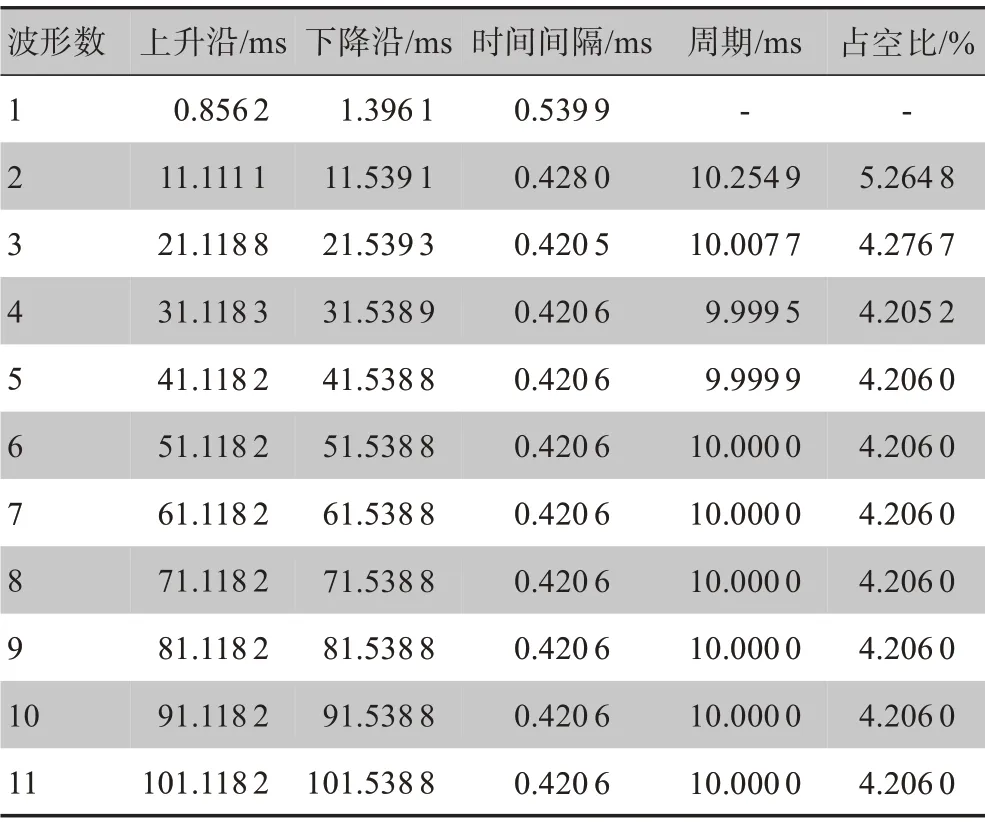
表2 截取常数为30 mV时的特征Table 2 Features at intercept constant of 30 mV

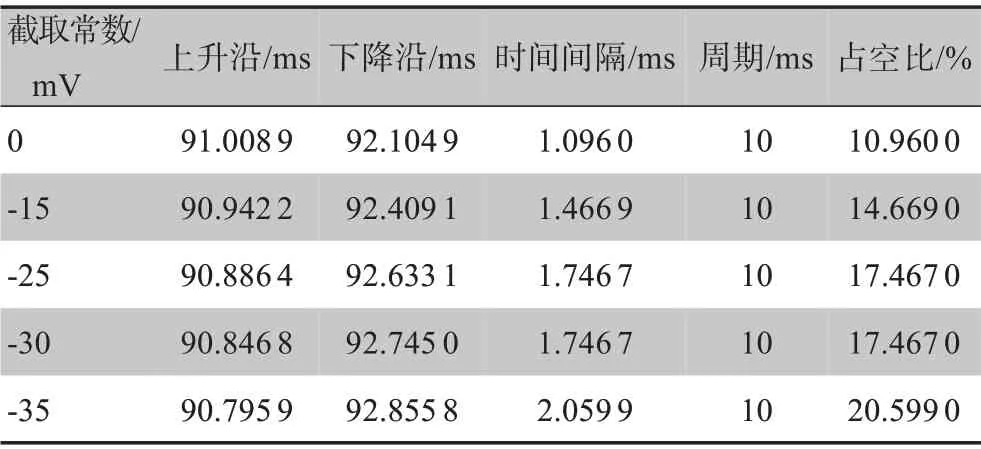
表3 不同截取常数特征Table 3 Features at different intercept constants

由于方波发生器的主要影响参数为HH 模型的参数，分析HH模型可知有6个影响因子分别为：钠通道最大电导GNa、钾通道最大电导GK、漏电导GL、钠通道反转电势ENa、钾通道反转电势EK、漏电流反转电势EL。本研究采用6因子3水平田口试验分析模型参数影响方波占空比的规律。根据神经元模型生理学参数取值分别设计出每个因子的3 个水平，见表4。试验首先要运用Minitab 软件进行田口设计，对各个因子和水平进行正交组合，然后根据因子组合进行试验，方波占空比作为试验响应。在Minitab 中共获得27 个正交组合L27（36），即需要完成27 组试验，试验各因子和水平见表5。

根据田口试验正交表进行试验仿真分析，以第1组试验为例，分析每个波形的特征，见表6。

由表6 数据可以观察到从第7 个波形数据开始周期和占空比都趋于稳定。为了保证稳定，以第10个波形特征为标准，周期稳定在10，占空比稳定在21.629%。根据第1组试验波形的特性，同理得到第2组到第27 组试验第10 个波形占空比响应，见表7。根据表7 的数据可以观察到第9 组占空比最小，最小值为19.946%。运用Minitab 软件对试验占空比响应进行统计学分析，见表8。

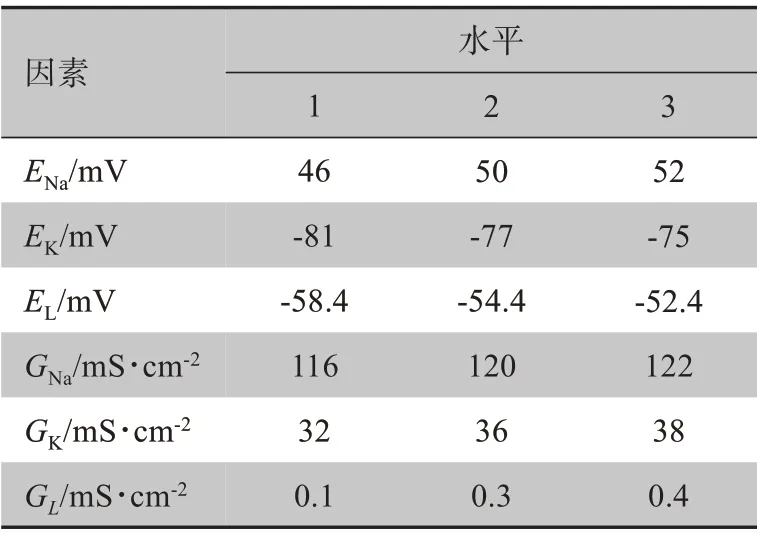
表4 田口试验参数设计表Table 4 Parameter design of Taguchi test

表5 田口试验正交表Table 5 Orthogonal array of Taguchi test

表8 为采用望小特性对占空比处理所得计算结果，由表8的数据可以计算得到因子水平对占空比的信噪比影响，见表9。表9中的Delta表示信噪比的极差值，极差值的大小反映了因子影响的重要程度，极差值越大说明因子对响应影响越大，反之因子对响应影响越小［19］。从占空比信噪比响应表可以观察因子对占空比的影响程度大小顺序为：GK＞GL＞GNa＞EK＞ENa＞EL。

表6 第1组试验数据Table 6 Test data in group 1

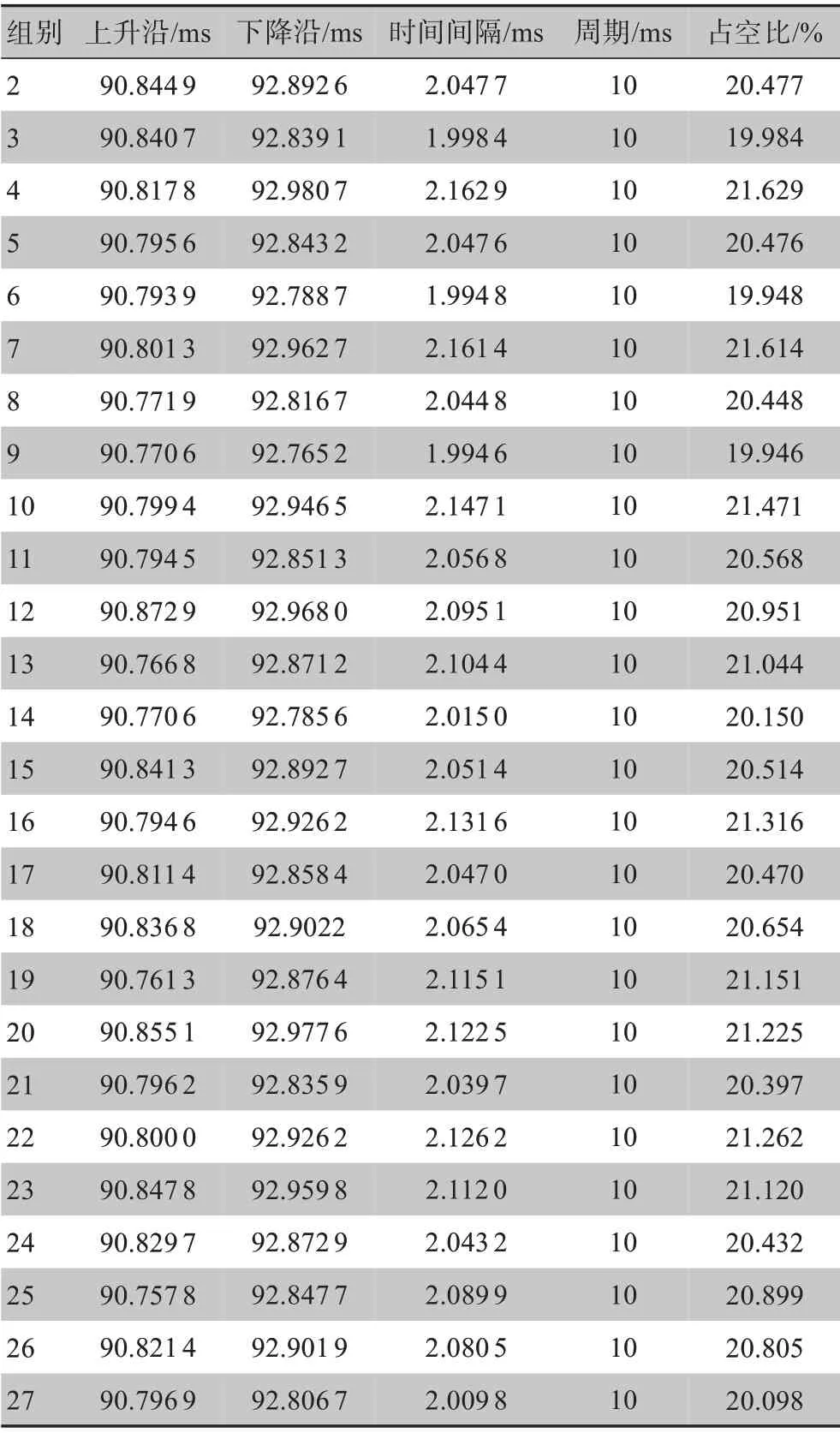
表7 第2组～第27组试验数据的响应特性Table 7 Response characteristics of test data from groups 2 to 27

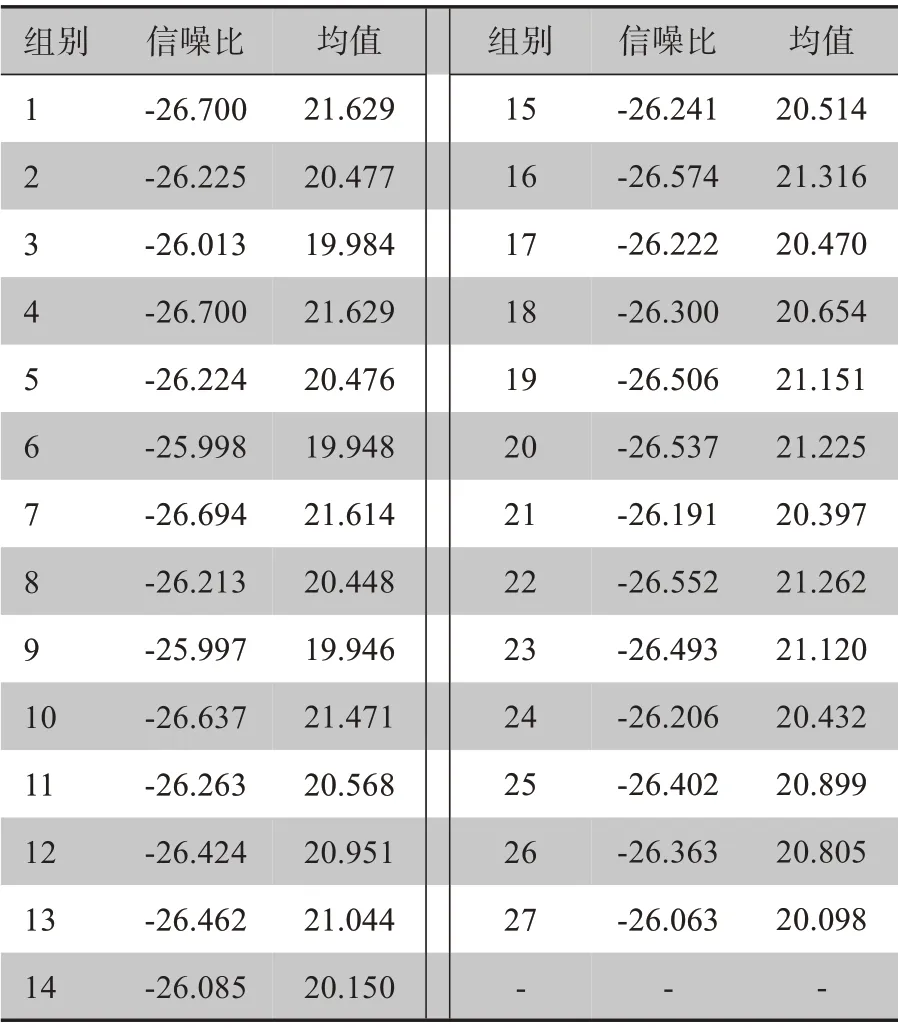
表8 信噪比和均值的计算结果Table 8 Calculation results of signal-to-noise ratios(SNR)and their mean values(dB)

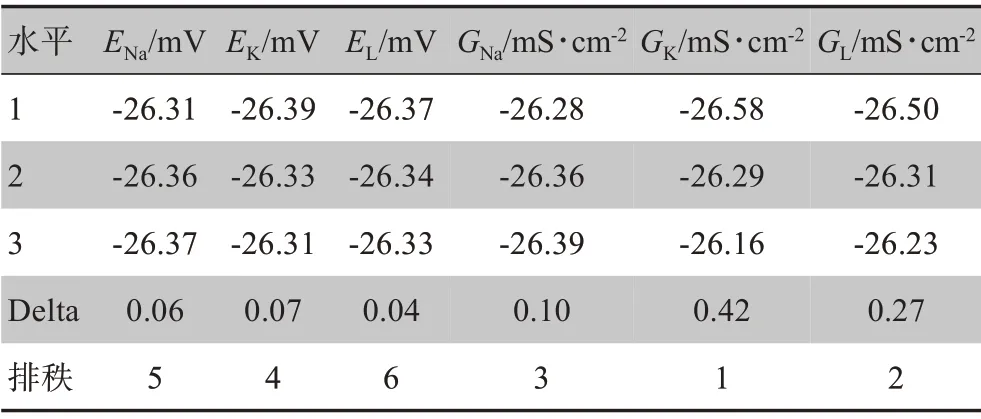
表9 占空比信噪比响应表Table 9 SNR response of duty ratio

在Minitab软件中还可以分析得到信噪比主效应图、信噪比残差图，如图6和图7所示。

由图6 信噪比主效应图可以观察到因子对信噪比贡献的程度和水平情况中信噪比的变化趋势；由信噪比越大越好可以得到最优因子组合（GK、GL、GNa、EK、ENa、EL）取值为：38、0.4、116、-75、46、-52.4。

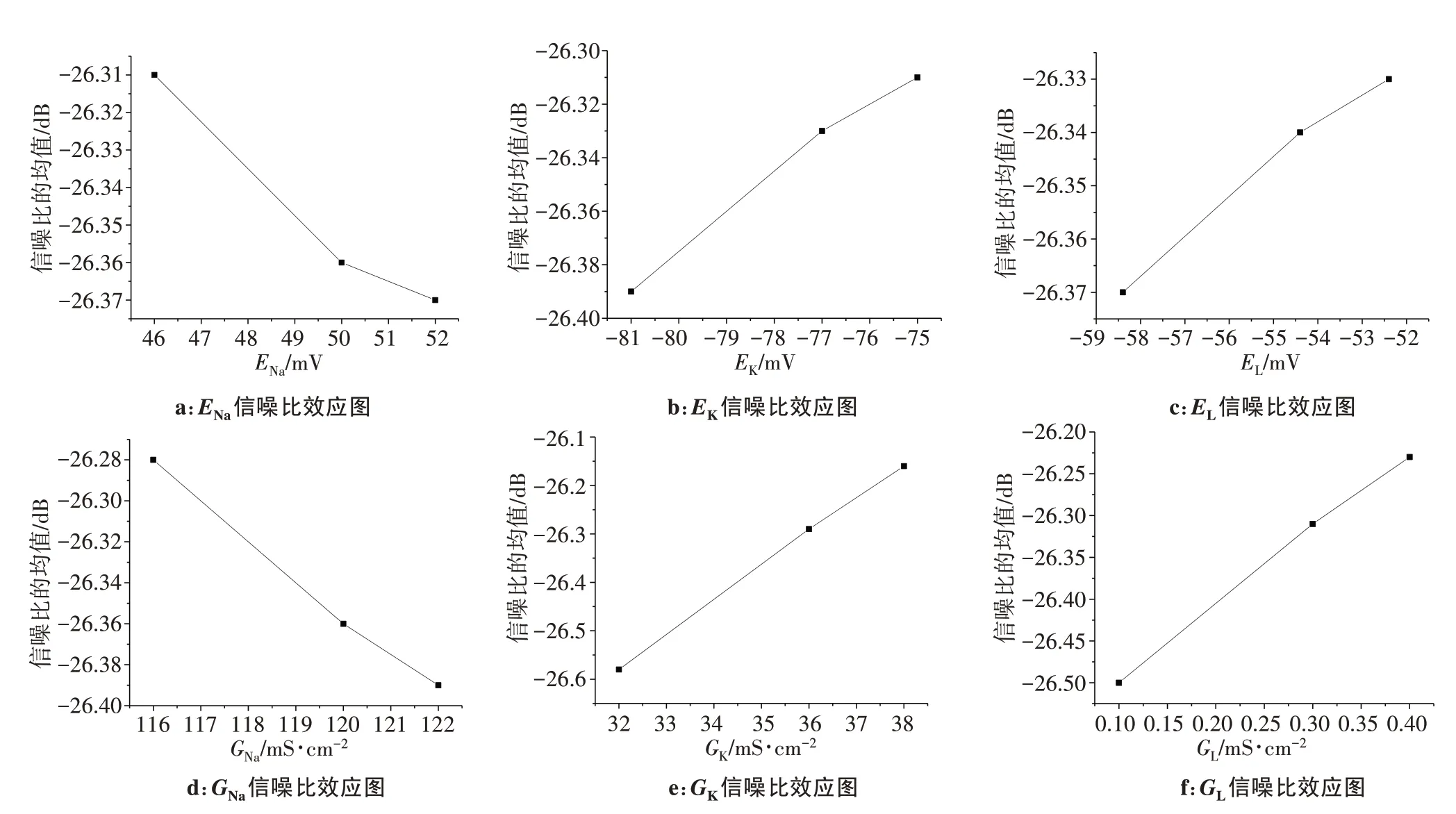
图6 信噪比主效应图Figure 6 SNR main effect diagrams

由图7 信噪比残差图观察可以得到以下结论：（1）正态概率图：均值和信噪比残差数值点分布近似一条直线，所以可以认定为正态分布；（2）直方图：残差的直方图近似为钟形曲线可以认定为过程稳定；（3）残差拟合图：数据点分布随机，没有异常点；（4）残差顺序图：数据点分布随机，没有异常点［20-23］。

利用田口法优化参数时通常根据方差分析确定因子对响应影响程度，根据表8的数据得到信噪比的方差分析数据见表10。其中Seq SS 为顺序偏差平方和；Adj SS为调整后的偏差平方和［24］。

在田口试验中为了判定各个因子的影响程度采用了统计学中的置信度，在田口法分析时通常取置信度大于等于99.5%，当P＜0.5%时，说明因子对实验结果影响显著，反之，因子对实验结果影响不显著。分析表10 方差数据可以观察到实验中的6 个因子的P值都小于0.5%，所以6 个因子都对响应指标有显著影响，都为重要因子［25］。根据上述方差分析得到重要因子，结合前面因子对结果的影响程度和根据信噪比主效应图得出的因子组合，可以确定优化方案为GK=38 mS/cm2、GL=0.4 mS/cm2、GNa=116 mS/cm2、EK=-75 mV、ENa=46 mV、EL=-52.4 mV。

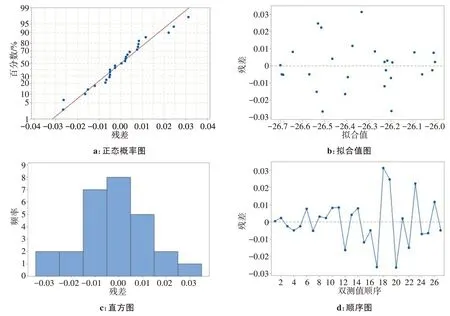
图7 信噪比残差图Figure 7 SNR residual graphs

表10 信噪比的方差分析Table 10 Variance analysis of SNR

最后通过Minitab软件中“预测田口结果”功能对上述所得到的因子组合进一步优化［26］，仿真结果见表11。由表11可以观察到采用正交方法的预测功能可以得到比设置因子和水平方案更优的组合，该组合可以使占空比更小，由设计组因子水平组的占空比19.9460%改变到优化方案因子水平组合的占空比19.7032%，实现了响应期望最小化。为了验证优化方案预测结果的正确性，利用图5的程序图得到仿真计算结果与预测结果对比情况，见表12。由表12可以观察到预测结果和仿真结果十分接近，相对误差仅为0.09%，因此可知利用田口方法预测得到优化方案和响应结果是可行的。运用Minitab软件进行田口试验分析基于神经元的方波发生器占空比规律，提高分析效率，减少试验次数，降低仿真的计算量。

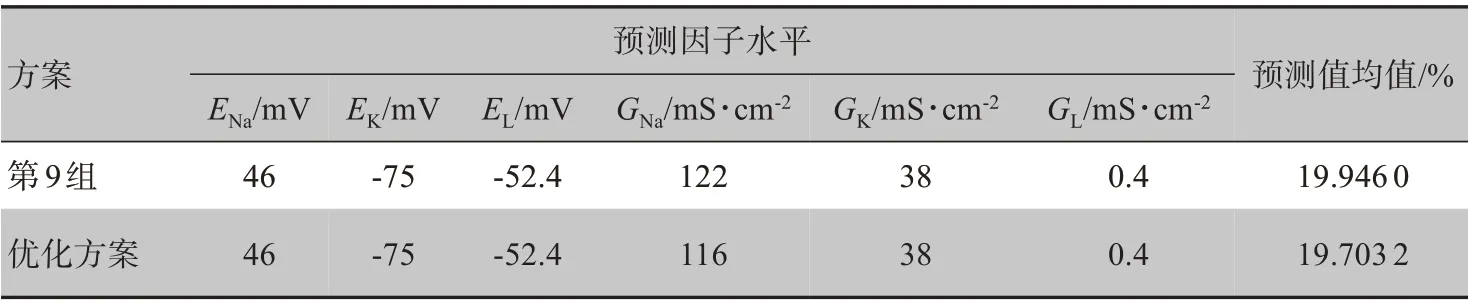
表11 田口预测结果与第9组数据比较Table 11 Comparison of Taguchi prediction results with the 9th group of data

3 结论

表12 优化方案仿真计算结果与预测结果数据对比关系Table 12 Comparison between simulation and prediction results of optimization scheme

本研究利用Simulink 工具箱，搭建了基于神经元的方波发生器仿真程序，基于田口法优化方波发生器的主要影响参数，得到主要结果如下：（1）研究方波发生器程序中不同的截取常数对方波的影响，发现方波波形初始阶段有较大的波动，随着仿真时间的延长，方波的占空比和周期趋于稳定值，这一现象说明基于神经元的方波发生器具有一定的自我调节性能；（2）利用田口法进行6 因子3 水平试验研究发现各因素对方波发生器影响的主次顺序为：GK＞GL＞GNa＞EK＞ENa＞EL；（3）根据田口法预测功能，得到最优影响因子及水平为：GK=38 mS/cm2、GL=0.4 mS/cm2、GNa=116 mS/cm2、EK=-75 mV、ENa=46 mV、EL=-52.4 mV，且优化方案的占空比为19.7032%，比原设计第9组方案的占空比19.946 0%还要小，实现了方波信号占空比最小化，该方波信号可为智能电子设备提供稳定抗干扰的方波信号。