在二次函数中巧搭学习支架触动数学思维
2022-05-30许文倩
许文倩

【摘要】二次函数是初中数学中的核心知识,教师通过巧妙搭建学习支架会活跃学生思维,促進学生灵活应用数形结合、分类讨论、方程、函数等数学思想方法.学生在探究中把握解题流程,灵活应用数学公式,在分析中强化思维活动,实现思维品质的提高.本文主要探究了在二次函数中巧搭支架触动学生的数学思维,落实核心素养.
【关键词】二次函数;学习支架;数学思维
《初中数学课程标准》指出要通过对实际问题的分析,体会二次函数的意义,理解函数的性质,学会推导方法,在实践中提高思维品质.学生主动探究和体验会更好地理解二次函数的基本概念,明确二次函数的图象性质,体会其中蕴含的模型思想,在思考中体会抽象概括和论证推理,主动地进行数据处理,实现思维品质的提高.
1 学习支架的类型分析
学习支架可以更好地帮助学生在二次函数探究中进行思考和分析,理解函数概念、性质、图象以及应用.它通过辅助的方式让学生成为课堂主人,活跃思维,通过推理判断的方式,掌握规律,让学生更好地理解知识.通过对学习支架的分析和总结,可以看到斯科隆将学习支架分为垂直式支架和连续型支架.而洪树兰把支架分为认知支架、情感支架、能力迁移支架.教师在课堂上要结合不同的教学内容选择不同的教学支架,引导学生解决学习上的疑难问题,促进主动思考,通过支架的帮助探究知识,实现学习能力的提高.
2 学习支架教学环节探究
在二次函数教学中,围绕着教学内容搭建支架式是组织支架教学的关键.
首先教师要认真分析二次函数概念、图象与性质,应用等知识的不同,结合具体教学内容精心设计脚手架,为学生搭建学习支架,促进学生主动过渡,向更高水平发展.
其次,课堂上设计不同的教学情境,激发学生的学习主动性,带领学生参与到课堂探究过程中,在不同的问题情境中抽象出二次函数模型,形成对知识的系统性认识.
再次,教师要用问题来激发学生思考的欲望,设计悬念,实现认知水平的逐步提高和过渡.学生在分析中会了解二次函数的图象、顶点、开口方向、对称轴等,形成对知识的客观性认识,逐步深化理解.
最后,通过学生的探究和思考,教师要评价学习结果,使学生了解自己对知识的掌握情况,提高解题能力,实现对数学与思维方法的掌握和提高.
3 不同类型支架在二次函数教学中活跃学生思维
3.1 利用问题支架去启迪学生思维
问题是启迪学生思维,点燃学生探究欲望的最好“催化加”.教师要积极地利用问题来创设情景,为学生搭建支架,激发学生的探究欲望,使学生主动地思考,开启对知识的探究.教师创设问题支架会使学生明确探究内容,了解探究目的,把思维转移到预设的知识上,进行深入分析和探究.
例如 在学习二次函数时,教师可以设计问题:“在同一直角坐标系中,函数y=a(x-h)2的图象与函数y=ax2的图象有什么联系和区别?”问题支架是活跃学生思维的关键,会让学生好奇,这种好奇心正是驱动他们思维和探究的关键,让学生主动思考函数y=ax2的图象的样子,考虑到图象的开口方向、对称轴、顶点坐标等,通过学生的绘画和思考,学生会想到y=a(x-h)2的图象就是将y=ax2的图象向右平移h个单位得到的.
探究中,学生会关注问题,将思维转移到问题中,围绕着探究问题进行知识的深入分析和思考,借助以往学习过的一次函数知识为铺垫,理解二次函数的图象,在分析中活跃思维,由已知知识转化为最近发展区,实现学生对知识的学习兴趣,在自主探究中借助问题支架去活跃思维,探究知识.
3.2 运用建议支架来发散学生思维
建议支架是将教师的意图和预设快速地交给学生,促进学生在建议中顿悟,产生灵感,实现对知识的理解.面对教师的建议,学生会从质疑、困惑中茅塞顿开,形成灵感,主动地探究知识.教师要结合学生的实际水平给出恰当的建议,做到符合学生的实际水平和能力.
例如 教师为学生提供试题:如图1,一个由半圆和矩形组成的窗户边框,上部分的半圆是由4个全等扇形组成的.制作这样一个窗户边框的材料总长是6米,如何设计才会使透光面积最大?
面对试题教师可以通过建议支架的方式来引导学生思考和分析,鼓励学生在建议中主动探究,教师可以给出建议支架1:如果能够总结出透光面积S与窗框尺寸之间的函数关系,就可以轻松解决问题.如何去设计这个尺寸呢?可以把它定为自变量x,所以问题就是解决自变量x与面积S之间的关系.
教师还可以给出建议支架2:透光面积是由哪两部分构成的?如果半圆的半径为自变量x,那么矩形部分的长怎样表示?怎样可以列出S关于x的函数关系式?通过建议支架的指导,学生会形成思路,在不断地建议中活跃思考,探究解题思路,寻找解题方法,建构函数关系.
教师还可以提供建议支架3:列出的S关于x的函数是哪一类函数?怎样求出这类函数的最大值或最小值?学生在建议支架中会理解到这个问题可以转化为函数最大值的问题,在思维活动的驱使下写出函数关系式.学生在建议的帮助下会把问题归结为二次函数问题,设出自变量和函数,并且写出函数解析式,包括自变量的取值范围,在自变量的取值范围内求出最值.
建议支架为学生提供了启发性建议,活跃了学生的思维,有利于学生在自主思考中主动探究,探究问题,掌握知识.
3.3 借助图表支架形象化学生思维
图表具有直观性和形象性,作为教学支架会给学生留下深刻印象,有利于学生一目了然地看到知识的来龙去脉,形成对知识的客观性理解.学生在图表支架的帮助下会形成直观性认识,完成知识意义建构,客观地探究知识,分析规律,在思维活跃中总结规律,在分析判断中进行逻辑思考,提高学习能力.
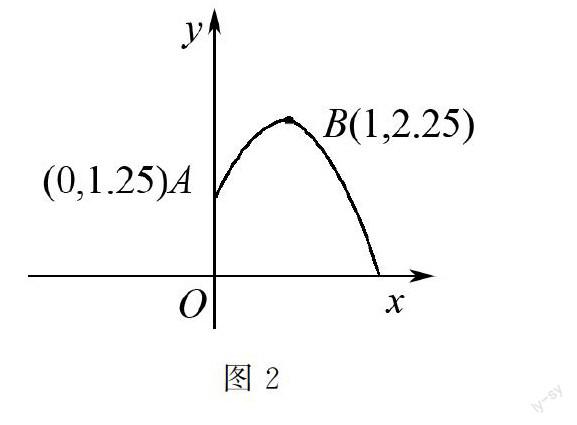
例如 在二次函数学习中,教师可以为学生提供练习题:某公园一圆形喷泉,水流在不同方向以抛物线的方式下落,建立直角坐标系,如果喷头所在A (0, 1.25),水流路线最高处B (1, 2.25) ,则该拋物线如何表达?水池的半径至少要多少米,才能使水流不会落到池外?为了使学生可以快速地理解题目要求,明确试题考查的内容,教师可以借助图表支架的方式来形象化学生的思维,用图表的方式给学生带来直观的印象和感知,促进学生形成客观性认识.学生在观察中会理解知识,主动思考,通过图表支架的帮助梳理相关信息,建构知识网路,联系相关的二次函数知识.
在探究中,学生会成为学习主体,思维处于主动状态,积极地绘画相关的图表,建立形象,形成主观性认识.学生在课堂探究中思维会非常活跃,建构形象思维和逻辑思维,在分析中感受到生活中的知识与二次函数之间的密切关系,在探究中形成客观性认识,理解知识之间的联系,把握知识本质,在探究中内化知识.
3.4 搭建认知支架深刻化学生思维
建构主义认为,学生对知识的认知具有一定的开放性,需要主动地建构,在不断地积累中深化对知识的理解,形成深刻性认识.在学生的主动建构中,教师要引导学生把相关的知识都结合起来,通过主动建构的方式来搭建知识框架,形成深刻认识.在不断地积累中,学生会理解知识.
例如 在学习二次函数过程中,教师要引导学生类比一次方程、一元二次方程、一次函數促进学生在主动地建构中理解函数概念.学生在主动地建构中会搭建认知支架,为学习建构一个桥梁,把已经掌握的知识和不了解的知识连接起来,形成主动性认知.学生在主动地积累和建构中会丰富自己的认识,主动开阔视野,形成对知识的客观性认识.
例如 在主动地建构中,学生会利用一次函数和反比例函数的图象绘制方式来探究二次函数的图象绘制方法,通过主动探究的方式进行列表、画坐标系、描点、连线,绘画出图象,形成客观性认识和主观性理解.
学生对知识的理解和认知就是这样一个主动搭建和绘画的过程,这会给学生带来成就感,促进学生在主动积累中获得丰富知识.在对二次函数的探究中,学生会认识到它就是类似于y=ax2+bx+c=0的函数,表达式的右边为二次整式,学生会主动地将自己对整式的理解进行回忆,主动进行知识的链接,在分析中把熟悉的知识和新知识联系起来,建立认知支架,理解新知识.
3.5 设计迁移支架去引导学生思维
数学知识的探究需要学生思维的参与,教师积极地引导会点燃学生的学习兴趣,促进学生思维的活跃,主动分析相关知识.
在对试题的分析中,学生会锻炼思维、拓展思维、开发潜能实现个性化发展,提高思维品质.在培养学生思维过程中,主动迁移知识会将学生的认知结构激活,将思维变为开放模式,实现学生主动探究,积极加工.
例如 在二次函数中,为了带领学生探究二次函数与x轴是否有交点,教师可以为学生提供一个具体的函数,之后引导学生令函数值为零,对函数进行求解,也就是求出函数ax2+bx+c=0的解.一个一元二次方程并不是一定有实数解,学生在大脑中就会想到要考虑它的b2-4ac.当学生形成了认知后,学生就会轻松理解知识.在这里就是为了让学生能够理解二次函数图象与x轴的交点情况而带领学生进行知识迁移而设计的支架,目的就是为了让学生在主动迁移中形成对知识的深刻认识,把握知识本质,形成客观性理解.
通过学生对知识的主动迁移和分析,学生的思维会变得更加活跃,主动联系以往掌握的知识进行迁移和分析,在探究中把握知识规律,理解知识本质.
在知识迁移中学生会主动探究问题,联系知识,产生学习动力,使课堂学习达到事半功倍的效果.学生在学习支架的帮助下,会进行发散思考,从多角度进行逻辑分析和推理判断,把以往的知识进行正向迁移,在加工处理中实现思维品质的提高,促使学生灵活解决问题,锻炼思维能力.
4 结语
总之,在二次函数学习支架的搭建和应用过程中,教师要注意到支架搭建的时机恰到好处,并且支架搭建考虑学生最近发展区,支架的设计符合学情锦上添花,使学生能够在支架的引导下产生探究欲望,主动思考.
学生通过逻辑思考和推理判断会活跃思维,促进思维得到锻炼,实现思维品质的提高.学生主动地积累和感悟会在实践中强化认识,提高理解能力,实现高效课堂.
参考文献:
[1]王新.初中数学综合题分析及教学策略探究——以二次函数综合题为例[J].试题与研究.2021,(35):19-20.
[2]陈吉,张爱平.初中数学“思维体验学习”的实践与反思——以《二次函数的应用》为例[J].中学数学杂志.2021,(06):23-27.
[3]环素云.把握概念核心,提升学生思维——“26.1.1二次函数”教学案例与评析[J]. 中学课程辅导(教师教育).2021,(07):84.
[4]高琼.知识建构 方法迁移 思想整合——以《二次函数图象的应用》为例谈深度教学[J].教学月刊·中学版(教学参考).2020,(12):26-28.
