基于应变信号时频分析与CNN 网络的车辆荷载识别方法

周云 赵瑜 郝官旺 方亮

摘要：针对现有神经网络车辆荷载识别方法的识别精度不足且训练样本采集困难的问题，提出了一种基于应变信号时频分析与 CNN 网络的车辆荷载识别方法，对移动车辆总重进行荷载识别.首先，利用连续小波时频变换方法处理桥梁跨中应变信号，得到应变信号的时频特征，并利用双线性插值算法将时频信号矩阵变为大小为64×64的数值矩阵，作为 CNN 网络的输入数据;其次，利用 CNN 网络的回归学习算法，在训练少量数值矩阵后直接建立应变响应与车辆荷载的映射关系，从而实现对未知车辆荷载的识别;最后，通过模拟试验发现虽然在不同路面粗糙度和噪声影响下，CNN网络的荷载识别结果会受到不同程度的影响，但在一定范围内的路面粗糙度和噪声影响下仍然能较精确地识别车辆荷载.

关键词：CNN 网络;时频分析;回归分析;车辆荷载识别

中图分类号：TU375.4  文献标志码：A

Vehicle Load Identification Method Based on Time Frequency Analysis of Strain Signal and Convolutional Neural Network

ZHOU Yun1，2，3，ZHAO Yu2，3，HAO Guanwang2，3，FANG Liang2，3，4

（1. Hunan Provincial Key Laboratory of Damage Detection，Hunan University，Changsha 410082，China;

2. College of Civil Engineering，Hunan University，Changsha 410082，China;

3. New System Research Center，Academician Zhou Xuhong，Hunan University，Changsha 410082，China;

4. College of Water Resources & Civil Engineering，Hunan Agricultural University，Changsha 410128，China）

Abstract：Aiming at the problems of insufficient identification accuracy and difficulty in collecting training samples in existing vehicle load identification method based on neural network， a vehicle load identification method based on time-frequency analysis of strain signal and Convolutional Neural Network （CNN） is proposed to identify the total weight of mobile vehicles. Firstly， the time-frequency characteristics of the strain signal are obtained by using the wavelet time-frequency transform， and the time-frequency matrix is changed into a 64×64 numerical matrix as the input data of CNN. Secondly， in order to realize the purpose of unknown vehicle load identification， the map? ping relationship between strain response and vehicle load is directly established after training a small number of nu ? merical matrices by using the regression learning algorithm of CNN. Finally， through simulation tests， it is found that although the load recognition results of the CNN are affected to varying degrees under the influence of different road roughness and noise， the vehicle load can still be more accurately identified under the influence of certain road rough ? ness and noise.

Key words：CNN network;time-frequency analysis;regression analysis;vehicle load identification

桥梁是现代交通的重要组成部分，在国民经济与民生生活中起着至关重要的作用.截至2019年，全国公路桥梁87.83万座，比上年增加2.68万座，其中，特大桥梁5716座，大桥108344座[1].相关研究显示[2]，我国2000年1月至2012年3月期间的157座失效桥梁的统计结果中，高达10.83%的桥梁失效是由车辆超载直接导致的.因此，实时监控桥面车辆重量，对于桥梁健康检测具有十分重要的意义.

2008年，李忠献等[3]提出了一种基于 BP神经网络的桥梁移动车载的分阶段识别方法，通过分阶段识别技术，对桥梁上的车辆的位置、速度和荷载等信息进行在线、实时地识别.利用有限元模型模拟了大量训练样本，采用正则化方法修正误差性能函数，通过遗传算法对初始权值进行优化，模拟结果表明：该方法识别精度高、收敛速度快，且具有较强的抗噪性和鲁棒性，但采用该方法训练 BP（Back Propagation）神经网络时需提前获得车辆的荷载时程信号.

2009年，Kim等[4]提出了使用人工神经网络（Ar? tificial Neural Network，ANN）作为桥梁动态称重（Bridge Weigh-in-Motion，BWIM）系统的信号分析算法，意在尝试从 BWIM 系统的时域应变数据中提取有关重型车辆的信息（例如重量、速度和轴数），并通过试验方法验证了该方法的可行性，但其荷载识别误差在±20%之间.

2012年，González等[5]通过在桥梁全跨布置多个称重传感器，利用监测所得的多个结构应变响应信号对传统 BWIM 系统测试方程中存在的病态项进行了消除，提高了对车辆实际轴重求解的效率，但该方法仍未摆脱传统 BWIM 系统高昂的设备以及后期费用问题.

2012年，夏樟华等[6]为了得到桥梁上移动车辆荷载，提出了一种基于应变响应与移动荷载回归方程的移动荷载识别方法.首先通过小波变换消除应变响应的噪声，其次通过响应特征估算车辆过桥的时间及速度，最后建立移动荷载与应变响应的二次回归方程.研究结果表明：该方法的误差率基本小于17%，但该荷载识别方法仍具有较大的识别误差.

2016年，赵华等[7]比较了连续小波变换（Con? tinuous Wavelet Transform，CWT）、离散小波变换（Discrete wavelet transform，DWT）和平稳小波变换（Stationary Wavelet Transform，SWT）对提高 FAD 信号车轴信息识别的特点、优势以及使用范围，提出了利用小波变换技术提高 FAD传感器对车轴信息识别精度的方法，并通过野外试验验证了该方法的可行性.但是，其仅对比了小波变换这一类时间频分析对于提高 FAD传感器的车轴信息识别精度的效果.

2016年，Bao等[8]通过测量在桥梁上施加外加荷载下桥梁结构的剪应变响应信号，并利用 BWIM 系统实现了对行驶车辆实际轴重的识别.

2017年，Lydon 等[9]基于光纤传感器，研发出了一种用于识别车轴的 BWIM 系统，该系统不但能获得准确应变响应信号，还能有效缓解噪声对测试信号的影响.

2020年，邓露等[10]为准确了解桥梁动态称重（ BWIM）技术在不同类型桥梁上的适用性，基于公路桥梁通用图集建立了典型截面和跨度的桥梁模型，并利用数值仿真方法研究了桥梁跨径、截面类型、车辆类型、传感器测点位置、路面平整度、测量噪声、行驶速度等重要因素对 BWIM 方法识别效果的影响，进一步验证了 BWIM方法的实际应用价值.

综上所述，相关学者的研究结果表明：采用神经网络对于车辆进行荷载识别能够避免传统 BWIM 系统需要安装复杂且昂贵设备的问题，但采用神经网络进行荷载识别时的识别精度有待提高，且训练样本的采集工作较为困难.因此，本文提出了一种基于应变信号时频分析与 CNN 网络的车辆荷载识别方法对车辆总重进行识别，避免为求荷载时程而需要提前采集荷载时程信号作为训练样本的弊端，同时，采用 CWT处理应变信号以提高荷载的识别精度.本文主要做了如下研究工作：首先分别利用短时傅里叶变换（Short Time Fourier Transform，STFT）、维格纳-维利分布（Wigner Ville Distribution，WVD）以及 CWT 变换对桥梁跨中应变响应进行时频分析，获得时域信号难以展示的时频特征，并生成大小为64×64数值矩阵;其次分别将上述时频分析方法生成的数值矩阵作为 CNN 网络的输入数据进行车辆荷载的训练识别，并选取训练识别效果最优的 CWT变换作为最终的应变信号时频处理方法，同时采用 CNN 网络的回归学习功能，在训练少量 CWT变换处理的数值矩阵后，直接建立输入数据与车辆荷载的映射关系，从而具备对未知车辆荷载识别的能力;最后通过车桥耦合试验验证了该方法的可行性.

1基于 CNN 网络的移动荷载识别

1.1时频分析

为将一维应变信号转化为能够输入 CNN 网络的二维数值矩阵，同时突出一维应变时域信号的频域特征，提高 CNN 网络对于应变信号特征的提取能力，本文需要将采集的原始应变信号进行时频变换处理.常见的时频分析方法有 STFT、WVD 和 CWT等.1.1.1 STFT 变换

Gabor 于1946年提出了 STFT 的概念[11]，通过對时域信号进行加窗处理，并对窗内信号进行傅里叶变换.通过在信号时间轴上不断地移动窗函数并不断地进行傅里叶变换，便可得到任意时刻 t 附近的时间局域化频谱.对于离散的时域信号 s [ n ]，STFT 的数学表达式为：

式中：κ[ n ]为窗函数;l 为窗长;x 为频率点序号;i为计数变量.

1.1.2 WVD 分布

WVD是一种行之有效的时频分析方法，被定义为信号中心协方差函数的傅里叶变换[12]，具有平移不变性、边界有界性以及可叠加性等诸多优点.

该方法能在时频域内保持较高的计算分辨率，同时，能够较好地反映信号的瞬时频率信息.对于信号 x （t）的处理过程的 WVD数学表达式为：

式中：xa （t）为原始信号;xa*（t）为的复数共轭.

1.1.3 CWT 变换

CWT作为小波变换的一种，对输入信号的类型无特殊要求，可对应变、位移及加速度等信号进行分析变换.CWT 变换具有较强的时-频定位能力，在结构健康监测领域内获得到了极大的关注.CWT 变化中最重要的步骤是选择小波基函数（Wavelet basis function），它直接影响后续小波分析的准确性和信号特征提取的有效性，其中常用的小波基函数主要有Morlet、Haar及其 Meyer等.根据相关研究表明[13]，采用Morlet基函数的 CWT分析方法在提取结构动态响应信号特征时具备更加理想的效果.Morlet小波基函数是具有呈平方指数衰减趋势的余弦函数，采用Morlet基函数的 CWT变换可表示为：

式中：ψ*（t）表示ψ（t）的复共轭.而Morlet小波基函数为一余弦函数，其在时频域的函数表达分别为：

式中：fb 为频率带宽参数;fc 为小波中心频率.

CWT 变换能够较好地从时间、频率及幅值等方面对非平稳信号的时频局部特征进行描述，还可以通过平移/伸缩窗函数的方式对信号细节特征进行提取，是一种较为理想的时频分析工具.

1.2 CNN 网络搭建

为了建立应变信号时频特征与车辆荷载的映射关系，本文提出了基于应变信号时频分析与 CNN 网络的车辆荷载识别方法.经过反复网络调节，在获得最佳训练识别效果后，本文选择了一个拥有4个卷积层、4个池化层、1个全连接层的 CNN 网络作为车辆荷载识别网络，网络中各部分作用[13]如下：

1）输入层（Input layers）.本文中的 CNN 网络输入数据是利用双线性插值算法调整应变时频信号大小后生成的二维数值矩阵，大小为64×64.

2）卷积层（Convolutional layers）.卷积神经网络中的每一层卷积层都有若干个卷积核，每一个卷积核中的参数都是通过反向传播算法最优化得到，且每个卷积核都承担着不同特征的识别任务，为获得最佳识别效果，经过反复网络调试，决定分别在第1层卷积层设置8个3×3卷积核，在第2层卷积层设置16个3×3卷积核，在第3层卷积层设置32个3×3卷积核，在第4层卷积层设置64个3×3卷积核.

式中：k 代表卷积核;Mj代表第j 个特征图;b 代表偏置;l 代表第 l 层.

3）池化层（Pooling layers）.池化也称下采样，存在于卷积层后面，其功能主要在于降低网络参数量.通过池化作用选择池化区域中感兴趣的值而舍弃其它值，即降采样，参与计算的数据量也会因此下降，在一定程度上达到了防止过拟合的目的.例如，“最大池化处理”作用是选择池化区域中的最大值作为输出值;“平均池化”作用是选择池化区域中的平均值作为输出值.本网络中采用的是“最大池化（max pooling）”.

4）激活函数（Activation functions）.卷积、池化等都是对数据的线性处理，为了使用 CNN 网络模型学习和理解复杂和非线性问题，需要在网络中引入非线性特征——激活函数.常见的激活函数有 Sig? moid、Tanh、Relu等，相比于 Sigmoid 和 Tanh 函数，Relu函数更加利于网络进行反向传播和参数更新，并且其还具有防止梯度消失的功能，因此本文中的激活函数将采用Relu函数.

5）全连接层（Fully connected layer）.在 CNN结构中，卷积层和池化层模仿着人类眼睛对目标局部特征搜索的效果，而全连接层会连接其前一层的所有神经元，目的是让全连接层可以整合卷积层或者池化层中提取的局部特征信息，提升 CNN 网络的识别性能.

6）输出层（Output layers）.常见的 CNN 网络主要有两大功能，即分类功能和回归功能.相比于分类 CNN 网络只能输出有限的几类结果，回归 CNN 网络则具备输出连续任意数值的能力.回归 CNN 网络将最后一层卷积层的卷积结果全连接到一个神经元上作为回归识别结果，如图1所示.

在回归分析中误差以及损失函数的计算式为式（6）.

式中：yi为训练数据中第i个数据的真实值;yi′为训练数据中第i个数据的预测值.

综上，本文将采用 CNN 网络回归学习方法，在训练少量车辆荷载值对应的应变信号时频数据后，直接建立车辆荷载与应变信号的映射关系，从而具备识别输出连续未知荷载的能力.采用的 CNN 网络结构及其网络参数设置如图2所示.

1.3车桥耦合数值模型

为建立 CNN 网络训练数据库，本文将建立如图3所示的车桥耦合模型，并通过数值模拟车辆以不同速度、不同荷载过桥时的桥梁应变响应.

在车辆建模中，充分考虑车身、悬架、轮胎等各部分的特性及其运动方式，并以弹簧阻尼系统为原型，将车辆各部分简化为由一系列质量、阻尼、弹簧组合而成的多自由度空间体系.以四自由度平面双轴车为例，建立车桥动力方程如下.

车辆子系统的振动方程可以表示為：

式中：Mv、Cv、Kv均为常系数矩阵;Fv+Gv为车桥接触点力对应的等效单元节点力，其取决于接触点的桥梁振动速度、振动位移以及车轮速度、位移等.

桥梁子系统的振动方程为：

式中：Mb、Cb、Kb均为常系数矩阵;Fb 为车桥接触点对应的等效桥梁单元节点力，其取决于接触点的桥梁振动速度、振动位移以及车轮速度、位移等.

其中质量矩阵为：

阻尼矩阵为：

刚度矩阵为：

式（9）～式（13）中参数的意义见表1.

本文将在Matlab平台中建立车辆子系统，并将车辆振动方程的右边项{ Fv }+{ Gv }施加于车辆子系统中各个自由度的节点上，并调用 ANSYS12.0的时程分析模块计算各子步时程.

第1步：预设桥梁子系统的位移、速度均为零，并以路面粗糙度作为激励，求解车辆子系统的解，即所有车轮与桥梁的接触力时程Fv （t）.

第2部：将第1步的迭代结果——接触力时程Fv （t）对应的等效节点力序列施加于桥梁上，并求解桥梁子系统，得到桥面的运动状态.

第3步：在第2步获得的桥面运动状态基础上，叠加路面粗糙度作为系统新的激励，并再次求解车辆子系统，得到车轮与桥面新的接触力时程.

第4步：计算第3步接触力时程与第1步（或前一次迭代）计算的接触力时程的误差，并判断是否满足迭代收敛条件.若满足，则代表完成了所有迭代计算，否则进入新一轮迭代过程，并重新计算第2至第4步.

第5步：迭代计算至达到收敛条件，将求解得到的迭代计算结果传递给 ANSYS 有限元模型进行求解，进而获得桥梁动应变响应时程.

1.4 面粗糙度模拟

在车桥耦合系统中，车辆内部振动激励源不仅来自桥梁挠曲变形，还来自随位置变换引起的不同路面粗糙度.而该粗糙度可以看做是一种平稳、各态零均值的随机高斯函数.一般情况下采用确定性函数模拟路面粗糙度分布，例如，功率密度函数（Power spectral density，PSD ），通过采集实际路面粗糙度数据后，通过拟合便能得到关于路面粗糙度的 PSD 函数曲线[14].

本文主要依据 ISO—1972规范建议标准，对路面粗糙度进行模拟，其表达式为[15]：

式中：Ω0为标准空间采样率;Ω为空间采样率，表示采样空间内，高频采样与低频采样的采样率分界线，通常取值大小为（π/2） cycle/m.

在实际模拟路面粗糙度时，通常采用相关级数理论，利用计算好的功率密度函数（PSD ）进行模拟，其表达式如下：

2数值模拟验证

2.1 车桥耦合模型建立

为了验证所提车辆荷载识别方法的可行性，本文建立了车-桥耦合计算模型进行模拟.通过Matlab R2019b 和 ANSYS 12.0分别建立了两轴车辆模型和桥梁模型，由Matlab主程序控制桥梁与车辆的子系统在每一个时刻进行耦合迭代至收敛，同时考虑路面粗糙度的影响，采用国家标准《机械振动道路路面谱测量数据报告》（GB 7031—2005） C 级路面[16]，最终输出行车道跨中节点的动应变时程响应.

本文根据研究的需要，采用两轴车的半车模型，如图3所示，考虑了车体浮沉、俯仰、两车轮竖向位移4个自由度，该模型基本能反映车辆各部分结构特性参数，符合本文研究中车-桥耦合模拟计算的精度，其车辆参数取值见表2.

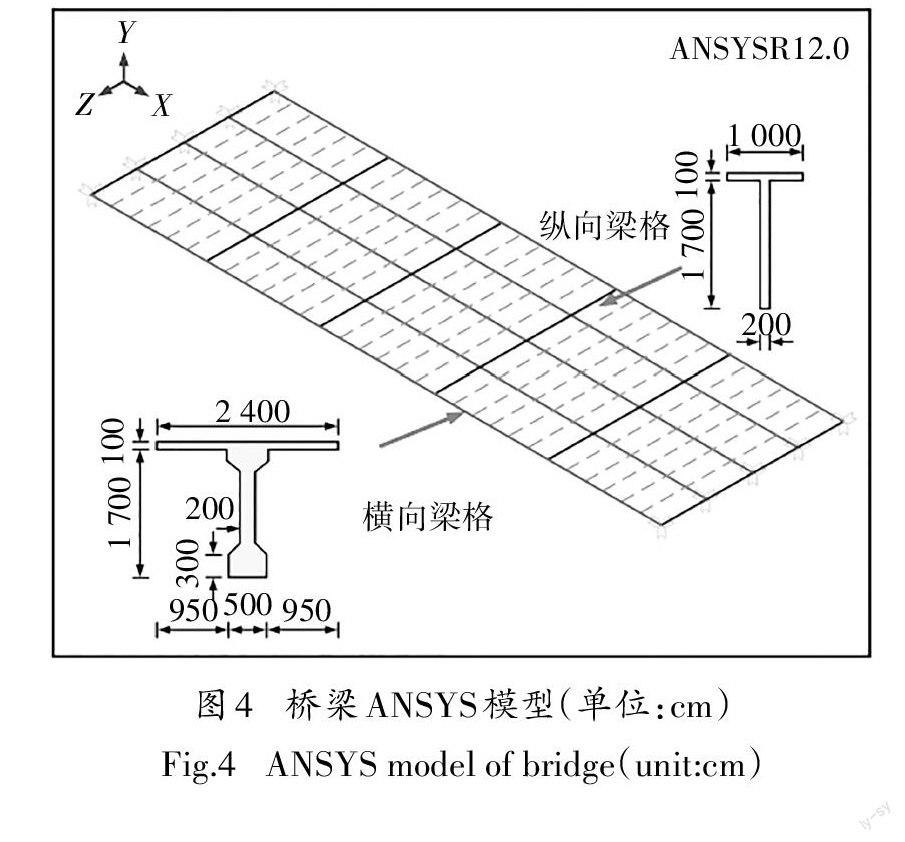
对于桥梁模型建模方面，采用钢筋混凝土梁板式桥梁结构，为了提高计算效率，在 ANSYS 12.0中采用梁格法利用纵横向梁单元建立整座桥梁结构体系，如图4所示.桥梁总长约30 m，宽度约12 m，由5根纵向 T 型梁组成，每根 T 梁的抗弯刚度为 EI=1.08×109 N·m2，质量阻尼系数α=1.76，刚度阻尼系数β=1.120×10-3.每隔6 m 设置横向隔板连接各纵梁，并且在该桥上对称设置两条车道，并将第一条车道作为模拟跑车车道.

为验证所提出的 CNN 网络对移动车辆荷载的识别效果，本文通过车-桥耦合模拟试验建立了 CNN 网络的训练数据集，模拟工况如下：首先，将车辆荷载分为2、4、6、…、38、40 t，共计20个荷载工况分组;其次，将每个荷载工况分组按照车辆速度分为5、5.25、5.50、5.75、…、14.50、14.75 m/s 等40个速度工况，总计20×40=800组工况;最后，进行模拟跑车试验，并选取具有代表性的跨中应变响应作为目标信号，部分跨中应变信号如图5所示，其中，原信号采样频率为100 Hz，图5为取原信号中1/10数据作图.

2.2应变信号时频分析

时频分析的基本思想是：设计时间和频率的联合函数，并且用该函数同时描述信号在不同时间和频率上的能量密度或强度关系.时间和频率的这种联合函数简称为时頻分布.利用时频分布来分析信号，能给出各个时刻的瞬时频率及其幅值，而幅值与信号能量有关，信号能量与输入激励有关，因此，合理地分析并表达出应变信号的时频分布关系，对于基于应变信号时频分析与 CNN 网络的车辆荷载识别至关重要.本文主要研究对比了 STFT 变换、WVD 分布、CWT 变换的应变信号分析效果.图6为4 t 重小车分别以5.0 m/s、6.0 m/s 的速度通过简支桥梁时，桥梁跨中产生的应变响应.

STFT 变换：STFT 通过对时域信号进行加窗处理，并分别对窗内信号进行傅里叶变换，获得特定时刻附近的时频图.而窗函数的应用能够有效地避免信号片段截取时的频率泄露问题，常见的窗函数有费杰窗、汉宁窗、海明窗等，本文采用常见的海明窗进行加窗操作，其中信号长度分别为692和581，窗长为128，重叠点数为127，采样频率为100 Hz，傅里叶点数为128，时频分析结果如图7所示.可以看出车辆经过桥梁时，对于应变信号低频部分的幅值有较大的影响，且随着车辆离跨中越近，应变幅值越大.从力学角度分析得知该幅值大小受车辆荷载大小影响，且由图7（a）和图7（b）可以看出，应变幅值对车速等因素并不敏感.

WVD 分布：WVD 分布具有平移不变性、边界有界性以及可叠加性等诸多优点.WVD 分析可以看作是信号自相关函数的傅里叶变换，它是信号的二次时频分析结果，因此，利用 WVD 处理应变信号，实际上反映了应变信号自相关函数的频域随时域的变化过程.本小节中，其对应变信号的时频分析结果如图8所示，其中，采样频率为100 Hz，信号长度分别为692和581.由图7和图8的分析结果可以看出 WVD 分析结果的数量级与 STFT 分析结果的数量级约成平方关系.

CWT 变换：CWT 变化中最重要的步骤是选择小波基函数，它直接影响后续小波分析的准确性和信号特征提取的有效性.CWT 变换能够较好地从时间、频率及幅值等方面对非平稳信号的时频局部特征进行描述，相比于 STFT 变换，CWT 变换可以通过平移/伸缩窗函数的方式对信号细节特征进行提取.本文选择Morlet小波对应变信号进行时频分析，其中，信号长度分别为692和581，采样频率100 Hz，最大尺度1000，时频分析结果如图9所示.从图7和图9可以看出，相比于 STFT 变换，由于 CWT 变换能自动调整窗函数以适应信号的变化，因此 CWT 的分析结果在低频时具有较高的分辨率，而且应变信号主要由低频信号组成，因此在处理应变信号时 CWT 变换是一种比 STFT 变换更理想的时频分析工具.

由以上时频分析结果可以看出，应变信号幅值主要由低频分量贡献，随着频率越高其对应变的贡献就越小.比较 STFT 变换、WVD 分布以及 CWT 变换对桥梁跨中应变信号的处理效果，可以发现 STFT 变换和 WVD 分布对该信号的处理效果较为一般，而采用Morlet小波的 CWT 变换在低频部分处具有较高的分辨率，能清晰显示信号间因为车速等因素不同而产生的微弱差别，更有利于 CNN 网络对于应变信号的特征提取.

2.3数值矩阵

从力学角度来分析，车辆荷载作用于桥梁桥体使得桥梁产生弯曲变形，桥梁跨中底部应变信号的信号幅值大小则间接反映了车辆荷载的大小，将一维的原始应变信号在频域中展开，能够在不同频率上更多地展示出应变信号与车辆荷载的间接关系，更加有利于 CNN 网络提取信号的相关特征，便于建立应变信号与车辆荷载的映射关系.为了更好地将上述特性用于 CNN 网络的训练中，本文采用时频数值矩阵而非时频图的 RGB 图像作为 CNN 网络的输入数据.

以 CWT 方法为例.图10（a）为时频分析所得数值矩阵的三维图，其中的元素值反映了真实的时频分析结果，且能反映两图间数值的绝对大小.例如，因为荷载大小的差异，图10（a）和图11（a）中的数值相差一个数量级，而图10（b）和图11（b）为时频分析数值矩阵转化为 RGB 图像后的像素值所作三维图，其中像素值范围在0～255之间，因此不能反映出原数值矩阵间元素的绝对大小.

综上所述，由于时频分析求得的数值矩阵元素大小与车辆荷载的大小相关，本文将采用双线性插值算法，将时频分析结果转化为64×64的数值矩阵作为 CNN 网络的输入数据，而非传统地将时频分析生成的 RGB 图片作为 CNN 网络的输入数据.

2.4神经网络训练测试

基于2.1节提出的车桥耦合模拟试验，在建立训练数据集后，利用 CNN 网络模型进行车辆荷载的训练识别验证.对于 CNN 网络模型，其输入数据为2.3节所示64×64的数值矩阵，且计算数值矩阵所涉及的时频分析方法参数取值与2.2节对应的时频分析方法参数取值一样.同时，CNN 网络的输出值为车辆总重值，即 CNN 网络输入数据为一个64×64的数值矩阵，输出数据为一个车重数值.

首先，随机选取每个荷载工况分组里的32组应变信号作为 CNN 网络的训练数据，选取剩余8组应变信号作为 CNN 网络的识别数据;其次，分别对上述数据进行 STFT 变换、CWT 变换和 WVD 分布生成大小为64×64的数值矩阵作为 CNN 网络的输入数据;最后，对比分析基于上述输入数据的 CNN 网络的训练识别结果，最终选出最有利于 CNN 网络训练识别的时频分析方法.

2.4.1 CNN 网络训练结果

由图12可以看出，基于 CWT 变换和 STFT 变换生成的时频数值矩阵作为训练数据的 CNN 网络，在经过大约50个迭代周期后损失函数收敛至0附近，均方根误差收敛至1000附近;而基于 WVD 分布生成的时频数值矩阵作为训练数据的 CNN 网络，在经过大约400个迭代周期后损失函数收敛至0附近，均方根误差收敛至1000附近.说明基于 CWT 变换和STFT 变换生成的时频数值矩阵作为 CNN 网络的训练数据更有利于 CNN 网络的迭代收敛，有利于提高 CNN 网络的训练效率.

2.4.2 CNN 網络对已训练荷载的识别结果

为验证 CNN 网络对于已训练荷载的识别能力，首先，分别从荷载工况分组为2、4、6、12、14、16、…、38、40 t 数据里随机选取30组数据，共计20×30=600组数据作为训练数据;再从每个荷载分组中余下的10组数据中随机抽取2组数据，共计20×2=40组数据作为识别数据;其次，分别利用 CWT 变换、STFT 变换、WVD 分布处理上述应变数据并生成大小为64×64的数值矩阵，并将其作为 CNN 网络的输入数据;最后，进行 CNN 训练、识别及其误差计算，其识别结果如图13～图16所示.可以看出，相比于 STFT 变换和 WVD 分布，基于 CWT 变换生成的时频数值矩阵作为训练数据的 CNN 网络，在识别已训练荷载值时的识别误差在±0.05%以内，说明基于 CWT 变换处理的应变信号更有利于CNN 网络对已训练车辆荷载的识别.

2.4.3 CNN 网络未知荷载识别结果

本节采用上述表现较为优异的 CWT 变换处理跨中应变数据，利用 CNN 网络的回归学习功能，在训练少量特定车辆荷载对应的应变信号时频数据后，直接建立起该数据与车辆荷载的映射关系，从而达到识别未知车辆荷载的目的.

首先，分别随机选取荷载工况分组为2、4、6、12、14、16 t 里的各40组数据，共计6×40=240组数据作为训练数据，同时分别随机选取荷载工况分组为8、10、18、20 t 里的各8组数据，共计4×8=32组数据作为识别数据;其次，利用 CWT 变换处理上述应变数据并生成大小为64×64的数值矩阵，并将其作为 CNN 网络的输入数据;最后，为排除数据选择对训练识别精度造成的误差，本文进行了3次识别数据的随机选择，并对 CNN 网络进行训练及识别验证，结果如图17～18所示.

由图17和图18可知，在经过训练学习 CWT 变换处理的应变信号数据后，该 CNN 网络已具备识别未知荷载的能力，且该识别误差大部分在±4%以内，满足实际工程应用的要求.

2.4.4路面粗糙对 CNN网络荷载识别的影响

由于不同的路面粗糙度会不同程度地影响车桥相互耦合振动的过程，因此为检验 CNN 网络在不同路面粗糙度下对车辆荷载识别精度的影响，本文按照式（15）模拟了5种不同等级的路面粗糙度，如图19所示，并用上述车桥耦合模型模拟了车辆以10 m/ s 的速度在该路面粗糙度下行驶时桥梁跨中的应变响应.采用上文已训练的 CNN 网络对该响应进行车辆荷载的识别，以检验其荷载识别精度，具体识别结果如图20和图21所示.

由以上识别结果可以看出，CNN 网络对于车辆在路面粗糙度等级为很好、好、中的桥梁上行驶时产生的桥梁跨中应变响应具有较好的荷载识别结果，其识别误差主要集中在-2%～5%的范围之内.随着路面粗糙度等级越差，其识别精度越低.

2.4.5 噪声对 CNN网络荷载识别的影响

由于应变信号在采集过程中，环境和仪器自身会对信号产生一定的噪声影响，且这一影响因素难以消除，因此需要研究噪声对荷载识别精度的影响.在本小节中，首先，模拟信噪比为1 dB、5 dB 和10 dB 的信号作为训练识别信号;其次，按照第2.4.2小节的训练方案训练 CNN 网络;最后，以车速为5 m/s 的信号作为识别信号检验 CNN 网络的荷载识别精度，其识别结果如图22和图23所示.

由以上结果可以看出，噪声对荷载识别结果会有一定的影响.当信噪比为1 dB 和5 dB 时，识别误差较大，局部误差接近50%;当信噪比为10 dB 时，噪声影响较小，误差基本在5%以下.

3 结论

本文提出了一种基于应变信号时频分析与 CNN 网络的车辆荷载识别方法，其具体步骤如下：首先，利用 CWT 变换对应变响应进行时频分析获得时域信号的时频特征;其次，利用双线性插值算法处理该时频特征数据，生成大小为64×64的数值矩阵作为 CNN 网络的输入数据;最后，利用 CNN 网络训练上述时频分析方法生成的数值矩阵进行车辆荷载的识别.同时，本文还比较了采用 STFT 变换、WVD 分布以及 CWT 变换处理的应变响应数据对 CNN 网络训练识别效果的影响，以及对比了不同路面粗糙度和噪音影响下 CNN 网络荷载识别的效果，最后得出以下结论：

1）相比于 WVD 分布和 STFT 变换，CWT 变换处理生成的应变信号时频数值矩阵更有利于提高 CNN 网络的荷载识别精度.

2）利用 CNN 网络的回归学习功能，在进行少量样本学习后，便可建立输入数据与车辆荷载的映射关系，从而具备识别未知车辆荷载的能力，且具有较低的识别误差.

3）模拟了5种随机路面粗糙度，并检验了 CNN 网络在不同路面粗糙度下的荷载识别情况，发现该 CNN 网络荷载识别算法在前3种路面粗糙度等级下，具有较高的荷载识别精度.

4）模拟了不同路面粗糙度和不同信噪比情况下，CNN 网络对于车辆荷载的识别精度，研究发现在前3种路面粗糙度等级以及信噪比较高的情况下， CNN 网络具有较高的荷载识别精度.

综上，本文提出的基于应变信号时频分析与 CNN 网络的车辆荷载识别方法拥有较高的荷载识别精度，对于桥梁健康检测具有一定的参考价值.

参考文献

[1]  中华人民共和国交通运输部.2019年交通运输行业发展统计公报[R].北京：中华人民共和国交通运输部，2020.

Ministry of Transport of the People′s Republic of China.2019 sta? tistical bulletin on the development of China′s transportation in ? dustry released[ R].Beijing：Ministry of Transport of the People′s Republic of China，2020.（In Chinese）

[2] 刘菠.高速公路桥梁典型病害及建管养对策研究[D].重庆：重庆交通大学，2012：30-35.

LIU B. Research on the typical disease of bridge and countermea? sure of construction management and maintenance on highway [ D]. Chongqing：Chongqing Jiaotong University，2012：30-35.（ In Chinese）

[3] 李忠献，陈锋，王波.基于 BP神经网络的桥上移动荷载分阶段识别方法[J].工程力学，2008，25（9）：85-92.

LI Z X，CHEN F，WANG B. A BP neural network-based stage identification method for moving loads on bridges[J]. Engineer? ing Mechanics，2008，25（9）：85-92.（In Chinese）

[4]  KIM S，LEE J，PARK M S，et al. Vehicle signal analysis using artificial neural networks for a bridge weigh-in-motion system[J]. Sensors （Basel，Switzerland），2009，9（10）：7943-7956.

[5]  GONZ?LEZ A，DOWLING J，O′BRIEN E J，et al. Testing of abridge weigh-in-motion algorithm utilising multiple longitudinal sensor locations[J]. Journal of Testing and Evaluation，2012，40（6）：104576.

[6] 夏樟华，宗周红，李嘉维，等.基于健康监测系统的大跨度连续刚构桥移动荷载识别[J].中国公路学报，2012，25（5）：95-104.

XIA Z H，ZONG Z H，LI J W，et al. Moving load identification of long span continuous rigid frame bridges based on health monitor? ing system[J]. China Journal of Highway and Transport，2012，25（5）：95-104.（In Chinese）

[7] 赵华，谭承君，张龙威，等.基于小波变换的桥梁动态称重系统车轴高精度识别研究[J].湖南大学学报（自然科学版），2016，43（7）：111-119.

ZHAO H，TAN C J，ZHANG L W，et al. Improved identification of vehicular axles in BWIM system based on wavelet transform[J]. Journal of Hunan University （Natural Sciences），2016，43（7）：111-119.（In Chinese）

[8]  BAO T F，BABANAJAD S K，TAYLOR T，et al. Generalizedmethod and monitoring technique for shear-strain-based bridge weigh-in-motion [J]. Journal of Bridge Engineering，2016，21（1）：04015029.

[9]  LYDON M，ROBINSON D，TAYLOR S E，et al. Improved axledetection for bridge weigh-in-motion systems using fiber optic sensors[J]. Journal of Civil Structural Health Monitoring，2017，7（3）：325-332.

[10]邓露，李树征，淡丹辉，等.桥梁动态称重技术在中小跨径混凝土梁桥上的适用性研究[J].湖南大学学报（自然科学版），2020，47（3）：89-96.

DENG L，LI S Z，DAN D H，et al. Study on applicability of bridge weigh-in-motion technology in short-to medium-span concrete girder bridges [J]. Journal of Hunan University （Natural Sci? ences），2020，47（3）：89-96.（In Chinese）

[11] GABOR D. Theory of communication. Part 1：The analysis of information[J]. Journal of the Institution of Electrical Engineers - Part III：Radio and Communication Engineering，1946，93（26）：429-441.

[12]许学明.改进的希尔伯特—黄变换及其在信号时频分析中的应用[D].南京：南京信息工程大学，2012：40-45.

XU X M. The improved Hilbert-Huang transform and its applica? tion in time-frequency analysis[ D]. Nanjing：Nanjing University of Information Science & Technology，2012：40-45.（In Chinese）

[13]赵丽洁.基于小波分析的工程结构时变参数识别研究[D].兰州：兰州理工大学，2016：41-46.

ZHAO L J. Research on time-varying parameter identification based on wavelet analysis for engineering structure[ D]. Lanzhou： Lanzhou University of Technology，2016：41-46.（In Chinese）

[14]唐海华，李琪，黄瓅瑶，等.基于 CNN 深度学习的径流预判方法及应用[J].水利信息化，2020（6）：37-42.

TANG H H，LI Q，HUANG L Y，et al. Runoff prediction method based on CNN deep learning and its application[J]. Water Re? sources Informatization，2020（6）：37-42.（In Chinese）

[15]何维.中小跨径梁桥动力冲击系数研究[D].长沙：湖南大学，2015：63—66.

HE W. Study of dynamic impact factor for medium and small span beam bridge [ D]. Changsha ：Hunan University ，2015：63-66.（In Chinese）

[16]机械振动道路路面谱测量数据报告：GB 7031—2005[ S].北京：中國标准出版社，2005.

Mechanical vibration-road surface profiles-reporting of measured data：GB7031—2005[ S]. Beijing： Standard Press of China，2005.（In Chinese）