让策略认知向青草更青处漫溯

摘 要：《数学课程标准》指出，教师在教学过程中需要帮助学生体验解决问题策略的多样性，形成解决问题的基本策略。“倒推”策略是一种特殊的教学策略，其要求教师引导学生用倒推（还原）的方法追溯问题的起始状态，分析与问题相关的数量关系等，这样不仅能有效增强学生运用策略分析问题的意识，提高其解决问题的能力，还能促进学生的逆向思维的良好发展。基于此，文章阐述了“倒推”策略的含义及其在解决问题中的重要性，并总结了几点引导学生掌握“倒推”这一问题解决方法的教学策略。

关键词：策略;倒推;认知

作者简介：贾青（1968—），女，江苏省南京市月牙湖小学。

我们都知道，事情从开始到结束需要一个过程。在这一过程中，事物要么是在数量多少上发生变化，要么是在方向、路线、时间等其他方面发生变化。研究其中蕴含的数学问题往往有两条线索：一条事物的起始状态开始，根据事物将要发生的变化，推断其结束时的状态;另一条以事物的结束状态为起点，根据事物已经发生的变化，追溯其起始状态。学生比较习惯用前一条线索分析数量变化关系和解决实际问题，但是有些问题用后一条线索来解决更为方便。后一条线索属于倒推思路。“倒推”，通俗地讲就是“倒过来想”，即从事情的结果往前追溯它在开始时是怎样的。“倒推”是一种策略，引导学生在事物变化中感受、体会、反思，应用不同的思路去解决新的问题。为促进学生的策略认知向青草更青处漫溯，本文结合《解决问题的策略——倒推》，总结了几点关于“倒推”策略的教学方法。

一、“倒推”策略的含义及其在解决问题中的重要性

“倒推”策略是一种以期望的目标为基准，从后往前来推测事物变化的策略方法。在以往的教学过程中，在分析和解决问题时，教师多习惯引导学生从现有的条件出发，根据条件分析和探索得出问题答案，即根据条件求出结果。而反过来，我们已知结果也能根据题目中的已知条件，通过反向推导求出事物先前的状态。但是，受传统思维的制约，很多学生并不了解“倒推”策略在分析和解决问题中的重要性，因此也不能很好地应用“倒推”策略解决问题。基于此，教师要帮助学生认识和理解“倒推”策略。本文是笔者结合课堂教学的具体案例和反思，经过研究和思考后得出的一些结论。本文结合具体案例《解决问题的策略——倒推》分析，力求学生能从数学的角度发现、提出和分析问题，综合应用所学知识解决问题，最终形成解决问题的策略。教学实践证实，创设与现实生活有密切联系的情景，能激发学生的策略意识;创设与“倒推”策略应用相关的数学问题，能使学生拓展思路;帮助学生进行自我比较、升华解题策略以及课后延伸，不仅能有效增强学生运用“倒推”策略分析问题的意识，也能提高其解决问题的能力[1]。

二、解决问题的策略——倒推教学策略

（一）创设与现实生活有密切联系的情景，培养学生策略意识

培养学生的策略意识，是促进学生策略认知“向青草更青处漫溯”的基础。我们在生活中时常会应用“倒推”这一策略，只是很多人没有对其进行系统性的理解与学习。学生有一定的生活问题解决经验，教师需要帮助学生提炼、总结“倒推”策略的一般思路，引导学生充分地理解这一生活内隐策略，使用简洁的语言表述其中蕴含的数学思想。为了激发学生运用“倒推”策略分析和解决问题的意识，在教学过程中，笔者依据实际生活场景设计了一个“教师找U盘”的问题情景，这一情景贴近学生生活，容易使学生产生共鸣，从而能激发其研究与探索问题的意愿。“教师找U盘”情景的主要内容为：教师上课时发现自己装有课件的U盘不见了，可是教师刚刚下公交车的时候，U盘还在她的口袋里，转眼就不见了，该怎么办呢？创设这样的情景后，笔者便让学生思考如何解决教师的问题。学生按照其惯性思维和生活经验，想到要找回教师丢失的U盘，最有效的方法就是原路返回去找。但是单纯知道原路返回去找这一方法还不够，我们还需要知道原路返回的路线。因此，笔者给学生出示了问题情境中教师的行动路线图，然后引导学生根据路线图思考和分析寻找U盘的最佳路径。最终，学生顺利帮助笔者在某个地方找到了U盘[2]。

（二）创设与“倒推”策略相关的数学问题，形成思路策略

培养学生运用“倒推”策略解决问题的意识后，教师还需积极创设与“倒推”策略相关的数学问题，并让学生运用“倒推”策略分析具体的数学问题，让学生逐步感悟基本的数量关系，帮助学生掌握具体问题情境中数字的变化，从而促使学生认识和思考问题的本质，进而能采用“倒推”策略有效解决实际问题。例如，笔者在教学过程中设置了倒果汁的问题。

1.设计“倒果汁”问题，让学生初步学习“倒推”策略的应用

“倒果汁”问题如下：甲杯中原来有一些果汁，被小红喝了50毫升后，又被倒入70毫升，现有220毫升果汁在杯中，那么甲杯中原有果汁多少毫升？在引导学生解答这一问题的过程中，笔者主要采用引导学生观察果汁变化示意图，应用“倒推”策略等方法帮助学生分析问题。学生通过观察“倒果汁”的示意图，可以很直观地發现杯中果汁含量的变化，学生依据自己的感性直觉获得了多样化问题解决方法。在学生通过自己的问题解决方法得出结果后，教师引导学生再倒回去检验，让学生理解“倒推”策略的合理性。最后，笔者帮助学生提炼出使用“倒推”策略解决问题的一般思路，使学生初步感受“倒推”策略的应用。在引导学生采用“倒推”策略分析上述问题的过程中，笔者先让其按题意有序整理题目中的已知条件，然后根据已知条件从最终结果“倒推”和反向计算，便能快速得到甲杯中原有多少毫升果汁，即220-70+50=200（毫升），从而帮助学生形成一定的“倒推”思路。待学生用“倒推”策略解决分析问题后，笔者还引导学生将利用“倒推”得出的答案代入问题，再进行正向检验计算结果，以进一步帮助学生理清思路[3]。

2.拓展设计“倒果汁”问题，强化学生对“倒推”策略的理解和运用

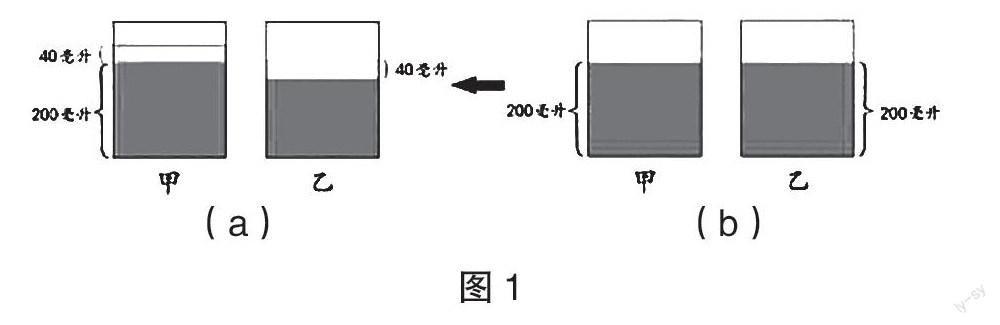
在上述解题过程中，学生采用“倒推”策略分析和解决问题，初步掌握了“倒推”思路，但是上述问题相对简单，学生对“倒推”策略的理解不够深入。为此，笔者进一步拓展了“倒果汁”问题，新的问题设计如下：有甲、乙两个杯子，老师这里有400毫升的果汁，准备按照图1（a）所示方法将果汁倒入甲、乙两个杯子，同学们觉得这样做公平吗？为什么？根据图1，学生可以直观地看到甲、乙两个杯子中所有的果汁量并不相同，因此，按照上述方法来倒果汁显然不公平。若甲杯往乙杯中倒入40毫升的果汁，两杯果汁量相同。那么两杯中原有果汁多少毫升？在这一问题的解决过程中，笔者将学生分为几个学习合作小组，让每个小组的成员先进行独立思考，然后再在小组内交流，勇于表达自己的解法和思路。通过自主探究，不少学生提出了自己的解法，如一学生的解题思路为：先预设平均分配后甲、乙两杯中分别有多少毫升果汁，即400÷2=200（毫升），再倒推甲杯：200+40=240（毫升），乙杯：200-40=160（毫升）。另一学生的解题思路为：可以先求甲、乙两杯果汁相差的部分：40+40=80（毫升）;再求乙杯：400-80=320（毫升），320÷2=160（毫升）;最后求甲杯：400-160=240（毫升）。建构主义认为，知识能否高效建构的关键是与新知有一定联系的旧知是否清晰。上述片段的教学中，笔者把教学的着力点放在“你是怎样解决问题的”这一主题上，以汇报的形式让学生展示自己的问题解决方法和结果呈现方式，使学生体验“倒推”策略。这样的方式能促使学生积极主动寻找不同的问题解决方法，自主感悟“倒推”的基本思路。这样的教学使学生产生了学习内驱力，其课堂参与效率自然就能获得提高，其课堂参与面也更广泛了[4]。

（三）注重学生在联系中的自我比较，升华解题策略

在学生基本形成解决“倒推”问题的思路后，笔者还设计了一些相似的题组，让学生自主观察和比较这些相似的题目，并判断哪些题组适合采取“倒推”策略来解决，进一步让学生明白适合采取“倒推”策略的问题情境。笔者设计了这样的题组：“小明原来有一些邮票，今年新收集了24张，送给小军30张邮票后，自己还剩52张。那么小明原来有多少张邮票？（题1）”“小明原来有一些邮票，他拿出邮票的一半送给小军，自己还剩24张，那么小明原来有多少张邮票？（题2）”“小明原来有24张邮票，他将自己一半的邮票送给小军，小明还剩多少张邮票？（题3）”笔者给出题组后，让学生思考解决这些问题的方法以及这些问题是否均能采用“倒推”策略进行解答。通过整理题目的已知条件，利用流程图表达题中的信息，不少学生能得知题1、题2可以应用“倒推”策略解答，如题1的信息流程图为“小明原有邮票x张→今年收集了24张→送给小军30张→还剩 52 张，因此，小明原有邮票数量为52+30-24=58（张）”;题2的信息流程图为“小明原有邮票x张→拿出邮票的一半（1/2x）送给小军→还剩24 张，即1/2x=24，可知x=48，即小明原有邮票48张”。而题3则不适合采用倒推策略进行解答，因为题3的信息流程图为“小明原有24张邮票→拿出邮票的一半送给小军→剩x张邮票，24-24×1/2=12（张）”，所以可以直接进行计算。引导学生观察和比较上述题组的原因在于现代教学论认为，学习不是学生对教师所授予的知识的被动接受，而是学生利用自身已有的知识和经验参与学习活动，历经知识的形成过程，主动实现意义建构。在上述知识建构的过程中，学生亲身体验了“倒推”策略，感悟“倒推”题型的特点、建构雏形，学会辨析，获得了丰富的学习经验[5]。

（四）课后延伸，进一步升华解题策略

为促进学生进一步感知“倒推”策略在问题解决中的应用，以及进一步深化学生对“倒推”策略的掌握，笔者还给学生布置了“李白饮酒题”的课后习题。早在1000多年前，我国唐代著名数学家张遂就对“倒推”策略进行了深入研究，并以“李白饮酒”为题材编制了一道可用“倒推”策略解决的问题，即“李白街上走，提壶去买酒。遇店加一倍，见花喝一斗。三遇店和花，喝光壶中酒。借问此壶中，原有多少酒？”利用“倒推”策略解题可知，壶中在李白最后“见花喝一斗”前有酒0+1=1（斗）;最后“遇店加一倍”，则原有1÷2=1/2（斗）;第二次“见花喝一斗”，原有1/2+1=3/2（斗）;第二次“遇店加一倍”，则原有3/2÷2=3/4（斗）;第一次“见花喝一斗”，原有3/4+1=7/4（斗）;第一次“遇店加一倍”，则原有7/4÷2=7/8（斗）。因此，此壺中原有7/8斗酒。

结语

引导学生采用“倒推”策略解决数学问题的过程中，教师应重视指导学生应用流程图整理题意。另外，教师还需要关注学生对“倒推”策略的感受、体验和理解，让学生体会“倒推”策略在解决特定问题时的优越性。学生在解决实际问题的过程中不断反思，感受“倒推”策略对特定问题的价值，其推理能力会得到进一步发展。总之，开展有关解决实际问题策略的教学，教师应遵循学生的心理特征和思维特点，从具体的问题出发，尊重学生个性，重视学生的感悟和理解，探寻有效的教学策略，发展学生的抽象思维能力，培养学生的数学素养。

[参考文献]

赵明.解决问题的策略：倒推[J].小学生学习指导：中年级，2016（17）：30，44.

毛应弟.浅谈“解决问题的策略：倒推”的教学与思考[J].小学教学参考，2015（18）：51.

翟明亮.解决问题的策略：倒推[J].小学教学研究（理论版），2015（5）：73-74.

柏德华.体悟·比较·选择：“解决问题的策略（倒推）”教学片段赏析[J].江西教育，2014（Z2）：69-70.

杨艳中.精当的板书 无声的教学：听徐斌教学《解决问题的策略（倒推）》有感[J].小学教学设计，2013（35）：47-48.