巧用轴对称性探求线段最值问题
2022-05-30袁国富
袁国富


轴对称图形是一种常见的平面图形。本章从生活中的图形入手,探究了轴对称图形的性质,并在此基础上进一步探索线段、角、等腰三角形的性质及相关判定,是初中数学的重要内容,也是中考考查的热点。其中,借助轴对称思想解决线段最值,即“将军饮马”问题,同学们往往因不会构造轴对称模型而无从下手。其实这类问题的本质是利用轴对称思想,将几条线段转化到同一直线上,利用两点之间线段最短或垂线段最短来解决。下面,就开启我们的探究之旅吧。
例 古希腊有一位数学家,名叫海伦。有一天,一位将军向他请教一个问题:从A地出发到河边饮马,然后回到B地,如何确定饮马点P,使得路程最短呢?
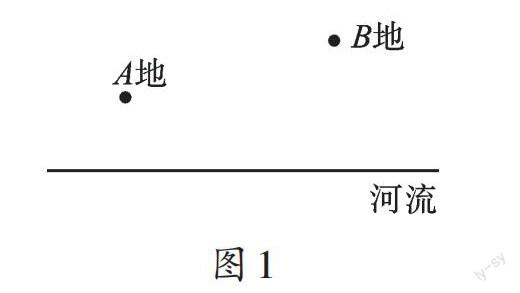
【分析】我们可以把这个实际问题转化为数学问题,即点A、B在直线l的同侧,如图1,在直线l上找一点P,使PA+PB最小。
我们不妨分析点P满足的条件,条件1是点P在直线l上,条件2是PA+PB最短。若直接连接AB,线段AB与直线l没有交点,要有交点则需将点A和点B转化到直线l的异侧。如何转化呢?我们不妨固定点B,此时在直线l的下方找到点A关于直线l的軸对称点A′。如图2,作点A关于l的对称点A′,连接A′B,与l的交点P即为所求。
为什么“PA+PB”是最小的呢?如图3,在直线l上任取一点P′(不与点P重合),连接P′A′、P′B。因为P′A′+P′B>PA′+PB,再由轴对称性可知PA=PA′,所以P′A′+P′B>PA+PB,所以PA+PB最小。
上述的最值问题源于著名的“将军饮马”问题,解决此问题的思想就是利用轴对称的性质化折线为直线,根据“两点之间线段最短”求最小值。攻略是先找一条定线,再确定两个定点,然后作其中一个定点关于这条定线的对称点,最后连接对称点与另一个定点,和直线的交点即为动点位置。此类问题可归纳为以下步骤:定线、定点、对称、连线、找交点。掌握了上面的最值模型,我们就来大展身手吧。
变式训练 如图4,在△ABC中,AB=AC=5,BC=6,点D是BC的中点,AD=4,点E和F分别是AD、AC上的动点,求CE+EF的最小值。
【分析】求CE+EF最小值,参照“将军饮马”模型,通过轴对称转化的方式来实现共线,确定最小值。根据等腰三角形的轴对称性可知,点C和点B关于直线AD对称,连接BE、BF,如图5。当B、E、F三点共线时,BE+EF最小,即CE+EF最小,最小值为线段BF的长。根据“垂线段最短”,即当BF⊥AC时,BF最小,所以求出AC边上的高BF,即为CE+EF的最小值。
几何学习中经常出现结构简单、内涵丰富的基本图形,我们可将其作为解题的基本模型,如本文所讲的“将军饮马”最值模型。在学习过程中,同学们不仅要能知模和用模,更重要的是理解模型背后的数学原理。“将军饮马”模型实际上是轴对称性质、“两点之间线段最短”和“垂线段最短”定理的综合运用,本质是运用轴对称进行等线段变换,再根据两个最值的知识源将折线化为直线,即可顺利破解。
(作者单位:江苏省建湖县汇杰初级中学)
