指向深度学习的小学数学单元整体教学

摘 要：指向深度学习的小学数学单元整体教学，遵循数学学科结构性、整体性和系统性的本质特征，顺应学生自主性、能动性和发展性的内在需求，彰显素养至上、育人为本和终身发展的价值追求。文章提出通过教材统整、单元组块和课堂变式三大策略，践行指向深度学习的小学数学单元整体教学，能够将已知、新知和未知有效联结，有效地提升学生的学习能力，使学生“既见树木，更见森林”。

关键词：深度学习;单元整体教学;小学数学

作者简介：林琳琦（1989—），女，福建省厦门市教育科学研究院附属小学。

著名特级教师张宏伟曾说过：“好的教学，让学生不止看见树，更要看见整个森林。”这就要求教师要有单元整体教学的意识，对学生的学习进行合理的整体规划，助力深度学习真正发生。接下来笔者将从“为什么”“是什么”“怎么做”三个方面来阐述指向深度学习的小学数学单元整体教学。

一、为什么——传统教学的现象扫描

教师在教学中经常会有这样的疑惑：教了，为什么还不会？学了，为什么不会用？变了，怎么又不会学了？产生上述现象的原因主要有以下三点。

（一）知识点散化

小学数学教材是根据学生的年龄和认知水平以单元为单位进行编排的，一线教师常常囿于教材单元，片面地一课一备，过于关注每个课时中的设计细节，很少思考知识之间的内在联系，忽略一节课的知识点在整个知识体系中的地位和作用，导致学生难以自主形成知识网络，不利于知识的迁移和学习能力的提升。

（二）教学应试化

教师忽视学生的主体地位，没有让学生亲历知识获得的过程，为达成教学目的，急于传授解题技巧，学生在还未亲历知识的产生过程，还不真正理解知识的本质的情况下，就进行题海训练。固化的浅层学习导致学生无法真正地内化知识、方法与学科思想，限制了学生在数学学习上的长远发展。

（三）流程机械化

传统教学常以“导入—新授—小结—练习”为授课流程，教学环节流于形式、浮于表面，学生逐渐对课堂学习失去兴趣，无法获得愉悦的学习体验，学习视野受到限制。教学流程不应该机械化，而应该围绕数学本质，以学习方法、数学思想为线索，以育人为目标展开学习活动。

综合以上三个方面，其核心就是学生的深度学习没有发生，而单元整体教学正是助力深度学习的一大抓手。

二、是什么——核心概念的内涵诠释

（一）深度学习

深度学习是指学习者在理解学习的基础上，批判性地学习新的思想和事实，并将它们融入原有的认知结构中，能够将众多的思想联系起来，将已有的知识迁移到新的情境中做出决策和解决问题的学习[1]。

（二）单元整体教学

单元整体教学是将具有结构关联的知识作为一个“系统”，以学生的“学”为中心，以“用”知识和方法学习新知、解决问题为目标，把具有相同或类似结构的一类课进行关联思考和整体教学设计，充分发挥和落实单元学习价值，以清晰的路径促进学生数学素养的提升[2]。

新课标研制专家组指出，我们的课程应当使学生真正感受到数学内容本身所具有的“整体性”[3]。单元整体教学正是促进深度学习的有利抓手，指向深度学习的小学数学单元整体教学以动态建构为核心，帮助学生自主完善认知体系，以发展学生的数学核心素养为方向，助力学生更加轻松地学好数学。

三、怎么做——课堂教学的实施策略

指向深度学习的小学数学单元整体教学是以整体关联为抓手的，以人教版小学数学四年级下册第三单元“运算定律”为载体，以该单元的难点——“乘法分配律”为切入点，阐述课堂教学的实施策略。以单元整体教学为抓手，注重从学生已有的知识、学习方法和经验出发，把数学知识和实际生活紧密联系起来，让学生在体验中学习，让学生参与知识的形成过程，培养学生概括、分析、推理的能力，并渗透从特殊到一般，再由一般到特殊的方法。

（一）融合——统整教材

通过串联教材、统揽全套教材、梳理全册教材、重构单元教材，对本单元教材进行分析。本单元的五条运算定律被誉为“数学大厦的基石”，这是学习整数领域的重要内容，能够为今后迁移到小数和分数领域打下基础。

“乘法分配律”是“运算定律”单元中的重点，知识点的编排很紧凑，运算定律将加法和乘法割裂开来学习。学生在之前的学习中积累了大量的经验，特别是加法和乘法的可交换性、可结合性。运算定律的教学旨在培养学生的数感、运算能力和推理能力。

1.纵向成串的领域内融合

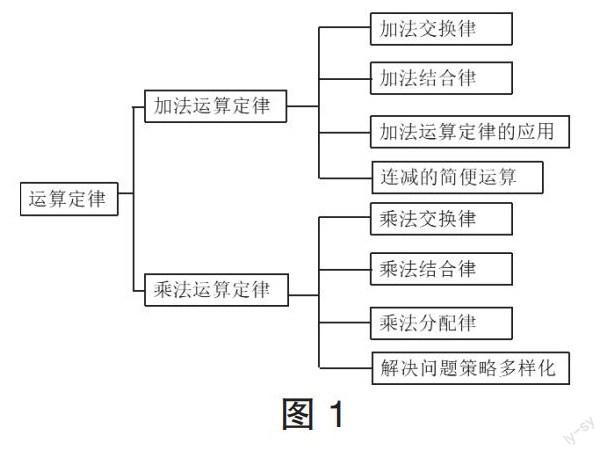
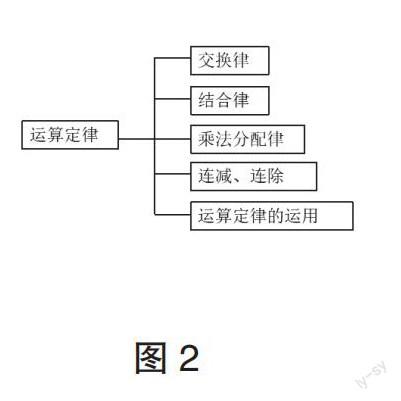
教材中，本单元知识点安排如下（图1）。在传统教学中，学习“乘法分配律”后，由于知识负迁移和知识点密集出现等原因，会产生运算定律混淆的现象。经过分析，对本单元知识进行如下重构（图2），将单元知识联系起来进行整体设计，实现纵向成串的领域内融合。“上下勾連”的策略有助于学生发现乘法分配律在本单元的逻辑关系。

2.横向成链的领域间融合

学生在学习“乘法分配律”之前的学习中积累了大量的经验，围绕单元知识之间横向成链的设计，采取“左右勾连”的策略，在课末通过回顾，将已知与新知联结起来，在不同的知识中发现相同点，提炼出模型——乘法分配律。联结不同单元之间的知识，有助于学生明晰数学的本质，完善横向成链的知识网状体系。

（二）组块——聚焦单元

1.立足方法结构，促进策略迁移

在学习起始课“交换律”的基础上，学生已经通过一个课时学习了加法交换律和乘法交换律，掌握了学习运算定律的方法，即“观察—猜想—验证—结论—产生新猜想”，以教学片段为例。

片段1：课开始时，教师借助起始课的板书（如图3）帮助学生回顾学习方法，激发学生的学习内驱力，促使学生积极运用这样的方法自主研究新的运算定律。

不少教师采用这样的迁移策略，但只是流于形式，给环节贴标签。而本节课，学生能在旧知和原有方法的基础上，真正地主动探究未知，明确探究过程所需要的条件。学生的学习意识从被动学习转变为主动学习，实现了从“学”到“用”的方法迁移，学生深度学习的“深”在主动发展。

片段2：课中探究，学生再次亲历“观察—猜想—验证—结论—产生新猜想”的过程。

立足于起始课，又不同于起始课。学生已经能用含有字母的式子来表示猜想，意识到用字母的表示方式更加简洁，通过计算结果来举例验证等。本节课，学生通过亲历知识的产生过程，在问题中增加知识的宽度，在思辨中增加知识的深度，在反思中增加知识的高度。学习指向从知识获得转变为问题解决，从“学会”到“会学”的学习迁移是深度学习的途径，为学生的可持续学习奠定了基础。

2.立足思维结构，彰显核心本质

片段3：课中反思，为什么在观察的这些式子中，等式的左右两边总是相等呢？

以往教师一看到学生能发现式子左右两边的结果相等，就停止探究了，导致学生只知其形，而不知其意。而深度学习的课堂，还要理解知识的核心本质。本节课采用多种方法来援疑质理、探究本质，让学生茅塞顿开。

方法1：结合解决问题的生活情境解释，如买套装、计算座位数、求大小长方形的面积等问题。

方法2：运用乘法的意义——用“几个几”解释。

方法3：推理。

（12+8）×5

=（12+8）+（12+8）+（12+8）+（12+8）+（12+8）

=12+8+12+8+12+8+12+8+12+8

=12+12+12+12+12+8+8+8+8+8

=（12+12+12+12+12）+（8+8+8+8+8）

=12×5+8×5

片段4：结构化。

回顾以前的学习过程，探寻乘法分配律的影子，建立知识结构（如图4）。

课末，学生通过联系已知、新知和未知，寻找乘法分配律的影子。不少教师会将旧知渗透在解决问题的情境中，但很少有教师会再反思，错过了思维的再次起跳点。本节课通过回顾与反思提炼出模型，进行结构化学习，有助于学生了解知识内容的框架与联系。横向领域内的知识结构关联，有助于学生“见树，更见林”。助力学生的学习层级从低阶认知转变为高阶认知是深度学习的目标。

（三）变式——立足课时

1.流程变式——教法活

片段5：在探索规律的教学中建立“观察—猜想—验证—结论—产生新猜想”这样的闭环式教学结构。

不同于传统的“导入新课—教学例题—巩固练习—课堂小结”，本节课在情境创设上以“抗疫”的大背景为主线，激发学生对“抗疫”英雄的感恩之情，培养学生的社会责任感。教学以“观察—猜想—验证—结论—产生新猜想”的闭环式教学结构展开，彰显了数学的本质特征，为学生今后的可持续学习奠定了良好的基础。

片段6：新猜想。

提出新猜想：其他运算会不会也有这样的规律呢？怎么验证？

（a○b）○c=a○c○b○c

c○（a○b）=c○a○c○b

课末，学生产生新猜想，是循着起始课的交换律的再猜想，提出是否有其他运算定律也存在类似的分配律。正如弗赖登塔尔所说的“学习数学唯一的方法是实行‘再创造”。当学生提出可以对新猜想继续延续“观察—猜想—验证—结论—产生新猜想”教学结构时，说明学生已经主动进行自我发展了，从“学会”到“会学”的结构已经形成闭环，这有利于挖掘后续学习的生长点，促进单元整体教学的延伸，使深度学习落地有声。

2.习题变式——思维新

片段7：说一说。

四年级学生参加植树活动，共有25个小组，每组有4人负责种树，2人负责浇树。一共有多少人參加植树活动？

小东的列式是：（4+2）×25=4×25+2，对吗？请说一说理由。

以上错例辨析是以植树为背景，有利于增强学生的劳动意识。找出“出错”的结点，通过联系具体问题情境、计算算式的结果、运用乘法分配律的模型等多种方式解释错处，能够促进学生深化认知，使其更加明晰乘法分配律的本质。

片段8：算一算。

观看无人机致敬“抗疫”英雄的表演视频，并谈谈感受。请用简便方法计算以下两道题。

（1）如果无人机一行102架，共15行，一共多少架？

（2）如果无人机一行99架，共18行，一共多少架？

以上练习循着乘法分配律是乘法对加法的分配，在解决这道题的计算时，运用简便计算，促使学生通过观察数据，变式运用，摸索出乘法分配律的变式。章建跃博士曾说：“为学生构建前后一致、逻辑连贯的学习过程，使学生在掌握数学知识的过程中学会思考。”这种设计强调将学生在学习过程中积累的经验迁移到新的问题情境上，深度学习的“深”构建由浅入深、逻辑连贯、拾级而上的学习过程。练习从浅层的应答到深度的思考，增强了学生的创新意识，为学生的可持续发展做了铺垫。

综上所述，指向深度学习的单元整体教学具有统筹规划、高屋建瓴的特点，它遵从了数学学科整体性、结构性的本质特征，顺应了儿童自主性、能动性的内在需求，彰显了素养至上、育人为本的价值追求。这就要求教师进行教材统整、单元组块和课堂变式，从“既见树木，更见森林”走向“通过研究一棵树，去认识一片林”，将已知、新知和未知有效联结，有效地提升学生的学习能力，助力学生全面建构数学知识体系，进而提升学生的数学核心素养。

[参考文献]

谢发超.导向深度学习的数学教学目标设计：以“函数的单调性”为例[J].中小学教师培训，2019（1）：41-45.

朱先东.指向深度学习的数学整体性教学设计[J].数学教育学报，2019，28（5）：33-36.

许卫兵.指向整体建构的小学数学教学[J].教育研究与评论，2019（4）：46-55.