培养几何直观能力 提升数学思维经验

摘 要：核心素养背景下，学生的几何直观能力与空间观念的培养受到了广泛的关注。对于学生来说，良好的数学识图能力不仅可以帮助自己积累数学知识，还可以提升自身的空间想象能力。教师要引导学生细致观察生活，让其将所学知识运用于生活中，提高实践能力。文章探讨小学中年级数学教学中对学生几何直观能力的培养，根据教学现状针对性地提出科学的教学策略，以期提升学生的几何直观能力和发散思维，为其未来发展奠定良好的基础。

关键词：几何;直观能力;数学思维

作者简介：冯强平（1981—），女，江苏省南通市海门区证大小学。

数学核心素养的内容较为丰富，其中就包括几何直观能力。要发展学生的数学思维，单纯采用“填鸭式”教学方式行不通，教师需要将数学学习与生活化实践相结合，引导学生使用所学数学知识解决生活中的问题。这样才可以在数形结合的教学中使学生发散思维，提升其几何直观能力。

一、问题提出

随着素质教育改革的推进，传统教学方式已经不能满足当前的人才培养需求，也不符合小学数学教学的要求。小学数学教材不断更新发展，其教学内容也更加注重图形图像。教师需要将数学知识和实际生活结合起来，统筹规划，整合零散的知识点，形成一个完整的数学知识体系。学生要在读图、析图、画图、用图的基础上，提升综合能力，为自己的发展奠定良好的基础[1]。识图不仅是表面意义上的“读懂图”，而且需要学生明确图的内涵与意义。学生要借助图形化思维解决实际生活中的问题，提高几何直观能力。教师要帮助学生发现图的主题或者找到图中隐含的数学信息，加强学生对实物和几何图形的联想能力;建立发现、分析、解决问题的问题探究路径，在动态化基础上提高学生的逻辑推理能力和空间想象能力，促进学生创新能力的发展。但是在实际教学中，部分学生的数学识图能力不甚理想，甚至有的学生对图形信息全然无感，在这种情况下，学生在涉及图形的数学问题中出错率较高。另外，有部分教师还在使用“填鸭式”教学法，没有对教学内容进行深层挖掘;还有教师忽略课堂中的交流与互动，在教学时生硬地传授知识，导致学生无法进行良好的知识消化，其一旦遇到复杂一点的问题就束手无策。教师只有从本质上提升学生高效读图、析图、画图、用图的能力，才能帮助学生理清思路，培养学生的几何直观能力。鉴于此，相关教育工作者需要认真思考如何培养学生的几何直观能力，以丰富其数学思维经验。

二、培养几何直观能力，丰富数学思维经验

（一）简化认识物体，把握数学本质

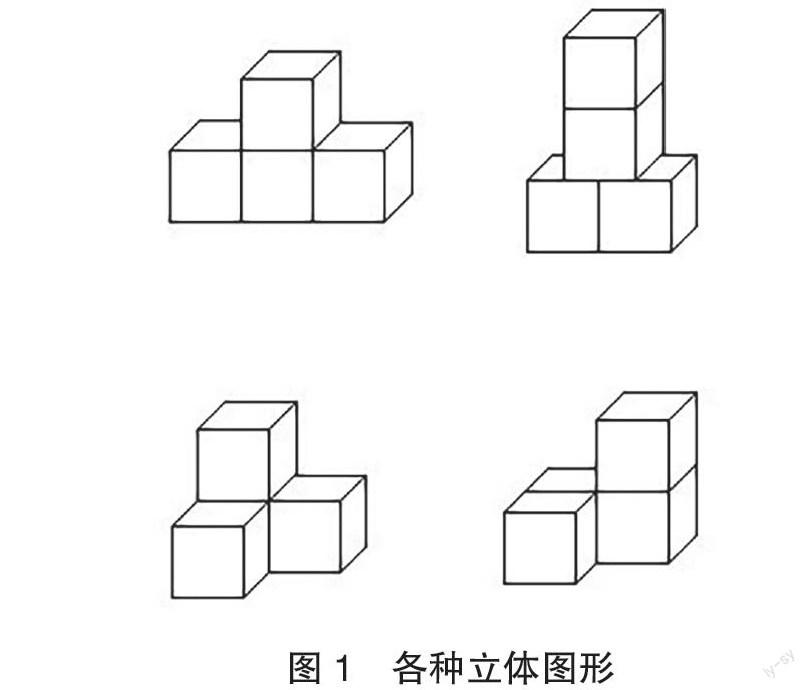
几何直观能力可以有效促进学生观察能力的发展，提高学生的问题分析能力和数学表达能力。数学比较抽象、复杂、内隐，教师只有将复杂的数学内容简单化，直观呈现隐含的数学信息，才可以让学生更好地理解数学。从本质上看，几何直观属于小学生数学形象思维的起点。对此，教师可以将直观图形资源和抽象数学资源结合，统筹教学内容，结合教学需要，将立体图形平面化，降低学习难度;使用以图促思的方式，化繁为简，帮助学生理解复杂的数学问题[2]。小学生的空间想象能力和抽象思维能力较弱，在学习相关空间知识时，需要加强对立体性的认知。教师要巧妙地、创造性地开展有效教学，开启学生的思维闸门，促进其形象思维向抽象思维过渡。在发展学生立体思维的过程中，教师要转换教学思维，以图促思，加强学生对物体特征的认知。例如，在学习“观察物体”相关内容的时候，教师就可以科学地引导学生，让学生使用四个大小一致的正方体摆出各种立体图形（如图1）。随后，让学生从正面、顶面、侧面等角度观察分析自己摆放出的立体图形有何异同。小学数学教师需要秉承科学的教学理念，帮助学生突破观察与思维的盲点。教师可以引导学生先使用纸张将这些立体图形围起来，在观察立体图形不同角度时再将相应的面揭开，使学生可以集中观察对应的平面图形，在反复的观察与探究中理解数学知识的内涵，并且在动手实践的过程中提高空间想象力和思维能力，进一步发展空间观念。最后，在知识巩固环节，学生可以通过刚才得出的平面图形组合成立体图形，以此巩固基础，找到规律，学会从不同角度观察事物、了解事物。

（二）形成“对面”观念，建立数形关系

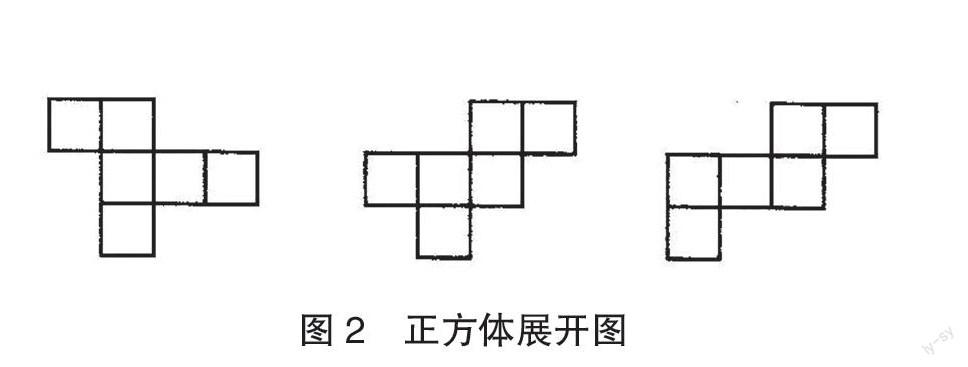
从本质上看，小学中年级数学学习起到了承上启下的作用。在此期间，小学数学教师不仅要传授数学知识，还要帮助学生建立良好的空间观念，突破几何能力培养中的难题。教师要引导学生形成“对面”观念，应用“对面”观念活跃学生的思维，培养学生根据物体特征学习几何图形的能力。例如，在学习“认识长方形和正方形”这一课时，小学数学教师可以为学生往后学习长方形和正方形的面积公式奠定良好的基础。首先，教师将学生合理地分为几个小组，让每一个小组都使用白色卡纸制作正方形方块。接着，在探究正方体表面积时，教师可要求学生将卡纸展开，帮助学生直观地认识正方体的表面组成，引导学生掌握其中的数学规律（如图2）。教师还可以引导学生在正方体各个面分别标注1、2、3、4、5、6，并根据数字分析其对应的是正方体的哪一块面，探究各个面的对应关系，将数字标注到立体图形上[3]。在这样的训练中，学生可以提高空间思维能力，把握空间与平面之间的联系，为今后的学习打下坚实的基础。

（三）有效理解表面积概念，获取数学信息

在素质教育背景下，传统、单一的教学方式阻碍了学生发散性思维的发展，使其難以真正做到数形结合。教师可以结合图形测量，加深学生对表面积等概念的理解。几何直观能力可以帮助学生观察事物，提高学生的问题分析能力，发展学生的数学表达能力。数学是抽象、复杂、内隐的，学生需要用直观的方式解决复杂的数学问题，简化数学关系。例如，在学习“长方形和正方形的面积”这一课时，小学数学教师可以使用多媒体技术，直观地展现长方体和正方体的表面组成，使学生在直观的认识中总结立体图形的数学特征。这样一来，教师不需要用过多的语言解释，学生便可以很好地理解本节课的内容，灵活地在抽象思维与具象思维中转换，通过平面图形理解物体的特征，为以后的学习和发展做铺垫，提升综合能力。

（四）在概念教学中培养学生的几何直观能力

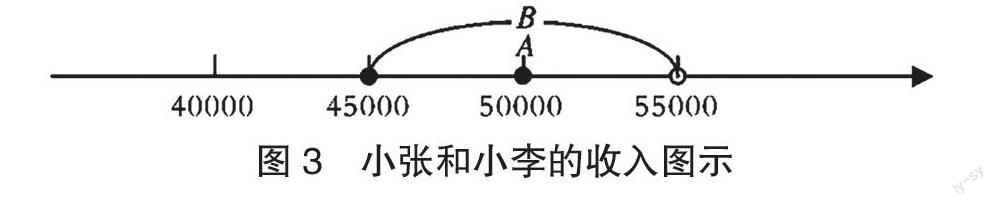
小学中年级的学生虽然具备了一定的知识基础，但学习经验不足，还不能很好地理解抽象的数学概念，其学习抽象概念比较困难。对此，教师就可以利用直观图形加深学生对概念的认识，解决问题，提高学生理解数学概念的能力，拓展其数学思维。例如，在学习代数的相关内容时，教师可以将数学知识和实际生活结合。鉴于小学生的思维以具象思维为主，在解决抽象问题的时候，教师要引导学生合理观察，培养其几何直观能力，促进其观察能力和问题分析能力的发展。针对小学生以形象思维为主的特点，教师需要先充分把握和理解数学概念，在教学实践中，将抽象概念转变为学生易于认知的内容，让学生更好地理解这些概念，有意识地将抽象数学语言与直观图形结合起来，加深对概念的认识和应用。如，有这样一道例题：小张和小李是邻居，他们各自拥有自己的一片果园。在一次聊天时，小张说，我的果园今年的收入刚刚好是5万元。小李听了之后说，我的果园今年的收入四舍五入之后是5万元。那么，小张和小李谁的收入更高呢？学生认真思考，给出自己的答案，并出现了三种不一样的结果表达。第一种表达，小张果园的收入正好是5万元，如果小李的收入大于4.5万元且小于5.5万元，那么这两个人的收入高低就不好确定[4]。第二种表达，小张的收入正好是5万元，那么小李的收入就处在4.5万元和5.5万元之间，小张的收入是确定的，小李的收入是不确定的，此时可以得出结论：45000元≤小李的收入<55000元。第三种表达，利用图形表现两个人的收入，此时学生可以观察到，小张的收入表现为一个点，而小李的收入表现为一个范围，一个点和一个范围之间是不能进行比较的（如图3）。在探究过程中，学生会发现第三种数形结合的表达方式可以更直观地解决问题，有效拓展数学思维。使用直观图形解决数学问题，不仅可以培养学生的几何直观能力，还可以有效提升其数学思维。学生经历了数与形的相互转换后，能在脑海中建立相应的数学知识体系，提升知识迁移能力。

（五）依托经验，激活空间表象

在实际教学中，教师需要结合学生的学习特点，激发学生的思维，将数学知识和实际操作有机结合。在设计教学时，教师需要激活学生的知识经验，化动为静，提升教学质量，让学生依托实际操作经验，激活空间的表象，经历静态想象，提高思维参与度。例如，在学习“图形的旋转”这一课时，教师可以利用多媒体演示时针从12时走到3时的过程（如图4），让学生思考：在这个过程中，时针转动了多少度？为什么是这个度数？有的学生会回答：时针一共转动了90度，12时与3时之间是一个直角，所以是90度。教师再继续问：时针是顺时针旋转还是逆时针旋转呢？学生回答：时针旋转的方向是顺时针。

结语

培养小学生的几何直观能力并不是一朝一夕的事情，教师需要坚持不懈，不断使用几何直观描述，帮助学生分析问题、解决问题，并找到对应的解题技巧;要给学生留出足够的时间思考，拓展其思维，体现其个性;要增强学生的空间想象能力，发挥数学概念在教学中的作用，提升学生的数学素养。

[参考文献]

汪春生.换位思考：从学生的视角看问题：《乘法分配律》的教学实践与思考[J].当代家庭教育，2018（1）：152.

杨豫晖，梁佩雯，杨彩莲，等.小学数学文化深度学习的教学结构探析：以“乘法分配律”为例[J].教育與教学研究，2020，34（7）：31-40.

丁玉华.以问题提出促进意义建构：“乘法分配律”教与学现状分析及教学建议[J].教育科学论坛，2019（4）：46-50.

卜彩丽，冯晓晓，张宝辉.深度学习的概念、策略、效果及其启示：美国深度学习项目（SDL）的解读与分析[J].远程教育杂志，2016，34（5）：75-82.