洛伦兹力冲量法及其应用

沈晓清

摘   要：洛伦兹力、动冲量是高考电磁问题的高频考点，从带电粒子只受洛伦兹力作用下的运动问题出发，通过正交分解在两个相互垂直的方向上运用动量定理，导出某个方向的位移与其垂直方向上的速度变化量成正比的结论，通过对比该方法与常规方法求解1道高考模拟试题和2道高考试题，凸显出该方法的优势，为求解与位移有关的一类电磁问题提供另一种思路。

关键词：洛伦兹力的冲量;动量定理;曲线运动

1  引言

全国高考物理学科考试大纲从2017年起，将物理试卷中选修3-5的动量模块由原来选考的考察方式改为必考。这无疑提高了动量这部分知识在高考中的地位与考察份量。统计分析2018-2021年，从各地高考试卷呈现的分值特点来看，动冲量的考察分值逐渐升温，这对一线教师如何开展动量模块的日常教学提出了新要求。带点粒子在匀强磁场运动问题一向是高考中重点考察的知识点，教师在教学过程中，往往采用“找圆心，定半径，画轨迹”，但这对学生作图与数学知识有一定的要求，洛伦兹力是变力，如果从动量的角度切入，用动量的方法去解决，相比于常规的方法可能会简捷许多。所以在日常教学中要注重学生灵活运用所学知识分析问题、解决问题的物理学科关键能力的培养，有意识地引导学生从动量的角度去分析、解决问题。本文介绍从动量的角度解决磁场问题的一个具体方法——洛伦兹力冲量法及其应用。

2  洛伦兹力冲量法

根据动量定理：物体所受合外力的冲量等于动量的变化量，即

I=Ft=p'-p=△p=mv'-mv

注意上述动量定理是矢量表达式，也可以运用到某一方向进行分解使用;下面从带电粒子垂直进入匀强磁场的情况下，运用动量定理导出洛伦兹力冲量法的简单形式。

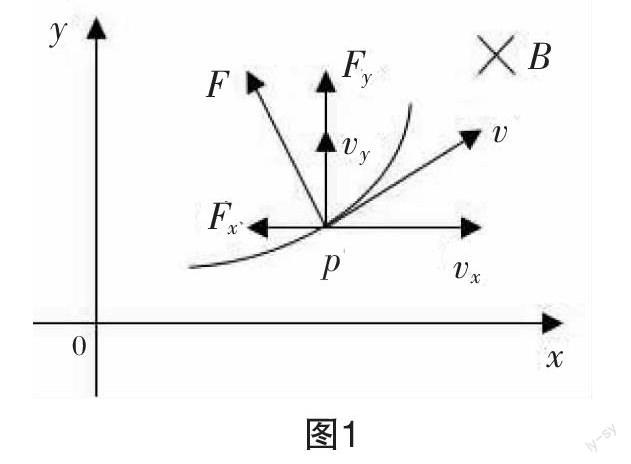
如图1所示，一带正电的粒子（不计重力）电荷量为q质量为m，在xoy直角坐标系中仅受洛伦兹力做曲线运动，磁场垂直坐标系向里，磁感应强度为B。粒子运动到p点处的速度为v，在x、y方向上的分速度分别为vx、vy，此时受到的洛伦兹力为F，其在x、y方向上的分力分别为Fx、Fy。其中F由v引起，由左手定则可知Fy是vx引起的，Fx是vy引起的，它们分别为

F=qBv   ①

Fx=qBvy  ②

Fy=qBvx  ③

考虑②、③式中Fx、Fy产生的洛伦兹力冲量得

FxΔt=qBvyΔt   ④

FyΔt=qBvxΔt   ⑤

对④式根据动量定理可得

FxΔt=mΔvx⑥

对④式累计求和可得

qBvyΔt=qBSy⑦

由⑥、⑦式得

qBsy=mΔvx=mv'x-mvx⑧

同理由⑤式可得

qBsx=mΔvy=mv'y-mvy⑨

⑧、⑨式中sx、sy的分别表示带电粒子在x、y方向上发生的位移，该位移与粒子在其反（垂直）方向y、x上对应发生的动量变化量有关;这里需要强调，上述式子均为矢量式，涉及正负号的问题，根据题目对速度的方向，电荷正负性，位移方向自行判断。此规律可以在涉及带电粒子位移与速度变化的相关磁场问题中应用。

上面介绍的情境中带电粒子只受洛伦兹力，粒子做匀速圆周运动，这类问题由匀速圆周运动规律就可以解决，是比较简单的情况。若带电粒子除了受洛伦兹力以外还受到其他力的作用，粒子在磁场中做的是复杂的曲线运动，还用常规的方法处理就比较麻烦。此时可以对带电粒子在仅受洛伦兹力的方向（垂直于恒力的方向）应用动量定理。为表达方便，称该方法为洛伦兹力冲量法。下面通过三道例题，演示这个方法在解题具体过程的应用。

3  洛伦兹力冲量法的应用

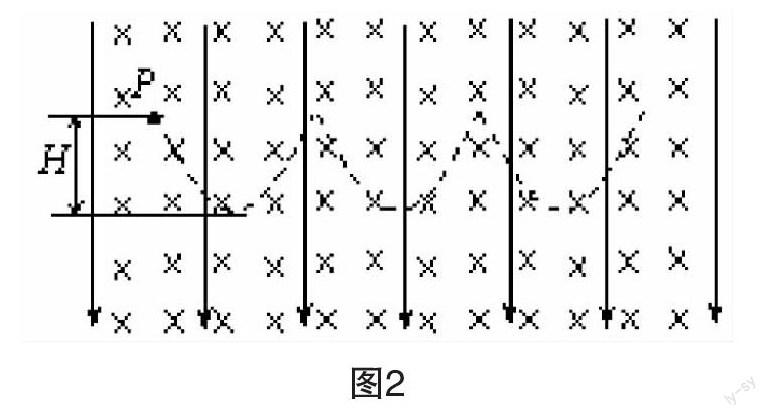
例1 [2018.北京海淀区高三一模] 空间中有相互正交的匀强电场（场强E）和磁场（磁感应强度B），电场方向竖直向下，磁场方向垂直纸面向里（如图2所示）。一质量为m、带电量为+q的粒子从P点由静止开始释放（不计粒子重力），粒子的运动轨迹如图中虚线所示。则粒子在电、磁场中下落的最大高度H为[ 1 ]（   ）

A.         B.        C.        D.

【解析】本题中给出的四个选项量纲各不相同，所以通过量纲分析，就可以找出与能量相同量纲的正确选项A。事实上对此题如果应用洛伦兹力冲量法，是可以直接求出H的表达式的。

设水平方向为x，竖直方向为y，粒子在水平方向上只受洛伦兹力Fx。可應用动量定理：

qBvyΔt=mΔvx             ⑩

对上式中粒子从p点运动到最低点的过程累计求和得

qBH=mv-m·0           11

粒子从p点运动到最低点的过程中只有电场力做功，由动能定理得

qEH=mv2-0         12

联立11、12式得

H=

【总结】由以上解法可知，洛伦兹力冲量法，不仅对于匀强磁场中做匀速圆周运动的带电粒子适用，而且只要带电粒子在某一方向只受洛伦兹力作用或除洛伦兹力以外的其他合外力为零，无论粒子是否做匀速圆周运动，洛伦兹力冲量法都在该方向上适用。

例2[2015.天津卷]如图3所示，真空中有多层紧密相邻的匀强电、磁场，电、磁场宽度均为d。电场强度E，方向为水平向右;磁感应强度B，方向为垂直纸面向里。电、磁场边界互相平行并与电场垂直，一带正电的粒子（质量为m、电量为q）于第1层电场的左侧边界某点从静止开始释放，粒子始终在电、磁场中运动，粒子重力与运动时产生的电磁辐射可忽略。该粒子从第n层磁场的右侧边界穿出时，速度方向与水平方向的夹角为θn，试求sinθn[ 2 ] 。

【解析】本题中有n层电、磁场，常规的方法是通过计算粒子通过前几层时的情况找出规律，依据此规律给出第n层的解并用数学归纳法证明之情况。或者直接从第n层切入，找出第n-1层与第n层的关系，得到递推公式，从而求解问题。常规方法计算繁琐费时费力对学生的数学能力要求很高。

解法一（常规方法）：

设第n层磁场中粒子运动速度vn，轨迹半径rn，则有

nEqd=mv

qvnB=m

当粒子运动到第n层磁场时，其速度方向和水平方向成αn角，粒子从第n层磁场的右侧边界穿出时，其速度方向和水平方向成θn角，垂直于电场的速度分量保持不变，则：

vn-1sinθn-1=vnsinαn

由r=得

rn-1sinθn-1=rnsinθαn          13

由图4可得

rnsinθn-rnsinαn=d           14

由13、14可得：

rnsinθn-rn-1sinθn-1=d

则可知r1sinθ1、r2sinθ2、r3sinθ3…rnsinθn，为一组等差数列，公差为d，可得：

d=rnsinθn=r1sinθ1+（n-1）d

当n=1时，由图5可知

r1sinθ1=d

则可得：

sinθn=B

解法二：（洛伦兹力冲量法）

在第一层磁场中粒子在竖直方向只受洛伦兹力的竖直分力，应用动量定理得

qbvxΔt=mΔv1y

积累求和得

qBd=mv1y-m·0

同理对第二层也可得

qBd=mv2y-mv1y

第三层

qBd=mv3y-mv2y

…

第n层

qBd=mvny-mv （n-1）y

对以上各式左右分别求和得

qBnd=mvny                 15

对粒子运动的整个过程动能定理得

qEnd=mv             16

联立15、16式解得

sinθn==B

【总结】相比常规方法，本题应用洛伦兹力冲量法求解，绕开了数学上繁琐的计算，物理过程一目了然，极大简化了问题的解答过程。实质上，洛伦兹力冲量法就是微元思想的体现，所以在高中阶段的考试中应用洛伦兹力法来求解相应题目并不算超出教材内容。

例3[2020.全国卷2第24题].空间中存在如图6所示的匀强磁场，磁场边界为0≤x≤h，-∝

（1）若粒子经磁场偏转后穿过y轴正半轴离开磁场，求磁感应强度的最小值Bm及其方向;

（2）若磁感应强度大小为，粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向及到x轴的距离[ 3 ]。

【解析】本题是带电粒子仅受洛伦兹力作用作匀速圆周运动，这类问题由匀速圆周运动规律及边界条件就可以解决，属于常规题型。

解法一（常规解法）：

（1）由左手定则可知：粒子进入磁场时受洛伦兹力方向向上，可知磁场方向垂直纸面向里。设粒子做圆周运动的半径为R，根据洛伦兹力提供向心力得：

qv0B=m       17

由此可得

R=       18

粒子穿过y轴正半轴离开磁场，圆周运动的圆心在y轴正半轴上，半径满足

R≤h           19

當磁感应强度大小为Bm时，圆周半径最大，即

Bm=              20

（2）如果该磁感应强度大小变为 时，圆周运动的圆心仍在y轴正半轴上，由18、20式可得运动轨道半径为

R'=2h

粒子的运动轨迹如图7所示，穿过磁场后从P点离开磁场，速度方向与水平方向成α角，则

由几何关系

sinα==        21

即α=               22

P点与x轴的距离为

y=2h（1-cosα）       23

联立22、23式得

y=（2-）h       24

解法二：（洛伦兹力冲量法）

（1）粒子穿过y轴正半轴离开磁场，当磁感应强度大小为Bm，R=h，在竖直方向应用洛伦兹力冲量法：

qBvyΔt=mΔvx

累计求和得：

qBm2h=mv0-（-mv0）

解得：

Bm=

（2）设粒子在P点的运动方向与x轴正方向的夹角为α，速度在x，y轴的分量分别为v0cosα、v0sinα该点到x轴的距离为y。

对洛伦兹力的竖直分力应用动量定理得

qBvxΔt=mΔvy

累积得

qBsx=mvy-m·0

代入：B==，sx=h，vy=v0sinα

解得

sinα=， α=

同理，对洛伦兹力的水平分力应用动量定理得

qBvyΔt=mΔvx

累积得

qBy=mv0-m·v0cosα

代入：B==，vx=v0cosα=v0

解得

y=（2-）h

【总结】本题考查要求虽然比较常规，用常规解法简单作图都能求解出来。但运用洛伦兹力冲量法可以省去“找圆心”“定半径”“找角度”的数学作图过程，对数学作图能力不好的学生提供了另一种思路。一题多解不仅可以训练学生的思维，还能提升学生对洛伦兹力冲量法认知水平，提高学生多角度思考问题，解决问题的能力及建模能力，培养物理学科的关键能力。

4  結论

动量定理作为处理力学问题的有力工具，在求解带电粒子在匀强磁场的位移问题时使用洛伦兹力冲量法往往绕开了数学上繁琐的计算，弱化对学生作图技能要求，使物理过程更为简洁清晰，增强学生学习物理的信心;对于较复杂的电磁运动问题，该方法更能凸显其优势，值得一线教师教学参考。

参考文献

[1] 陈宝友.对高考试题中的“无法定量求解”问题的解法归类[J].中学物理教学参考，2017，46（Z1）：37-41.

[2] 金邦建，黄胜，杨德明.高考物理天津卷压轴题的多种解法[J].课程教学研究，2016（3）：80-83.

[3] 宋小羽，麻永斌.模型引领  专项突破——电场与磁场问题应答策略[J].招生考试通讯（高考版），2021（3）：12-16.