“铅垂高、水平宽”巧解三角形面积

吴琼

真题呈現

在平面直角坐标系中，已知A（1，1），B（7，3），C（4，7），求△[ABC]的面积.

解析：如图1，过点C作y轴的平行线，交AB于D，过点B作DC的垂线，垂足为F，

过点A作DC的垂线，交CD的延长线于点E，

[S△ABC=S△ACD+S△BCD=12CD?AE+12CD?BF=12CD （AE+BF）]，

此处AE + BF即为A，B两点之间的水平距离.

由题意得AE + BF = 6.

由A（1，1），B（7，3）得直线AB的解析式为y = [13]x + [23]，

由点C（4，7），可得点D（4，2），

所以CD = 5，[则S△ABC=12CD（AE+BF）=15].

模型构建

如图2，A，B两点之间的水平距离称为“水平宽”;

过点C作x轴的垂线与AB的交点为点D，线段CD即为AB边的“铅垂高”.

结论：[S?ABC=水平宽×铅垂高2].

运用铅垂法时的辅助线引法：

（1）如图2，取AB作水平宽，过点C作铅垂高CD.

（2）如图3，取AC作水平宽，过点B作BD⊥x轴交直线AC于点D，BD即对应的铅垂高，[S△ABC=S△ABD-S△BCD=水平宽×铅垂高2].

（3）如图4，取BC作水平宽，过点A作铅垂高AD.

还可横竖互换，在竖直方向作水平宽，在水平方向作铅垂高.

（4）如图5，取BC作水平宽，过点A作铅垂高AD.

（5）如图6，取AC作水平宽，过点B作铅垂高BD.

模型应用

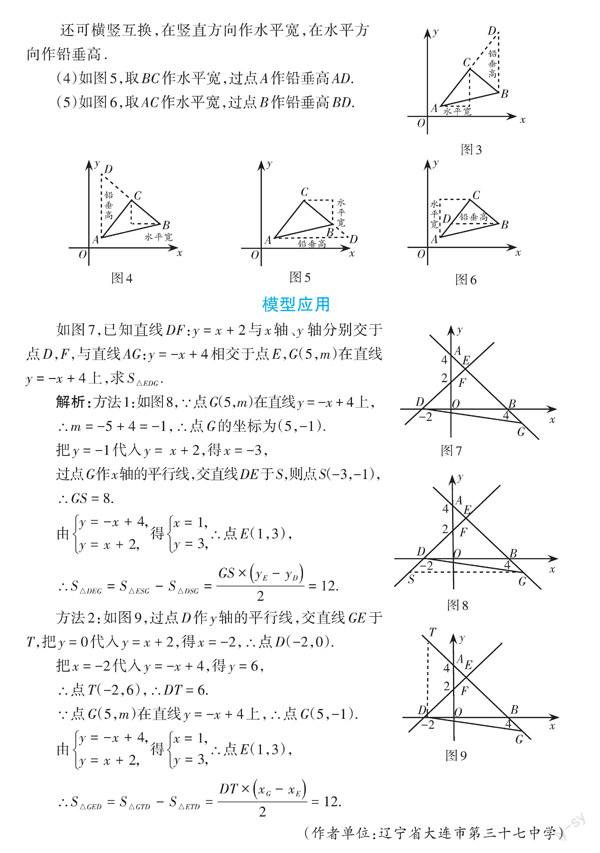
如图7，已知直线DF：y = x + 2与x轴、y 轴分别交于点D，F，与直线AG：y = -x + 4相交于点E，G（5，m）在直线y = -x + 4上，求[S△EDG].

解析：方法1：如图8，∵点G（5，m）在直线y = -x + 4上，

∴m = -5 + 4 = -1，∴点G的坐标为（5，-1）.

把y = -1代入y =  x + 2，得x = -3，

过点G作x轴的平行线，交直线DE于S，则点S（-3，-1），

∴GS = 8.

由[y=-x+4，y= x+2，]得[x=1，y=3，]∴点E（1，3），

∴[S△DEG=S△ESG-S△DSG=GS×yE-yD2=] 12.

方法2：如图9，过点D作y轴的平行线，交直线GE于T，把y = 0代入y = x + 2，得x = -2，∴点D（-2，0）.

把x = -2代入y = -x + 4，得y = 6，

∴点T（-2，6），∴DT = 6.

∵点G（5，m）在直线y = -x + 4上，∴点G（5，-1）.

由[y=-x+4，y= x+2，]得[x=1，y=3，]∴点E（1，3），

∴[S△GED=S△GTD-S△ETD=DT×xG-xE2=] 12.

（作者单位：辽宁省大连市第三十七中学）