指向数学文化的问题链教学设计与实施原则

唐恒钧 李佳薇

【摘 要】数学文化的视角从多个方面为数学问题链教学带来了新的认识，因而指向数学文化的问题链教学在设计与实施中需要遵循数学关联的多重性、数学问题的境脉性、问题解决的实践性等原则。

【关键词】数学文化;数学问题链;教学原则

笔者在《数学文化的教学意蕴及问题链的价值》中，探讨了问题链在为学生体会数学发展的文化动因，感受数学的文化价值，体会数学的文化系统时具备的价值[1]。那么，为了彰显数学文化，数学问题链教学又该如何设计？要回答这个问题，我们先来思考一个具有基础性的问题，即数学文化这一新的视角能给数学问题链教学带来哪些新的认识？

一、数学文化视角下问题链教学的新认识

从文化的视角看数学，呈现了更完整、更全面的数学面貌。其中既包含作为文化活动静态结果的数学知识体系及动态过程，也包含促动数学发生发展的文化动因，还包含数学在人类文明进步中发挥的重要文化力量，形成了一个关于数学产生发展的动因、过程、结果以及发挥文化力量的完整谱系。这为更全面地认识数学教育的价值提供了视角。数学教育的目的不仅仅是数学知识的传承，也不仅仅是数学思维的训练，而是一种以数学知识为基础，包含数学方法、思想、精神于一体的数学素养的涵养。正如喻平对知识教育与文化教育间的关系进行分析后指出的，文化教育是知识教育的拓展，将教育内容从知识扩大到整个文化，强调的不仅仅是让学生学习静态的知识，还要使学生受到学科文化的全面熏陶，包括对创造知识的源泉、动态的历史过程的认识，形成科学的理想、信念、精神、价值观和人生观[2]。

尽管我们过去在关于数学问题链教学的研究中，也充分地认识到数学教学的文化实践性以及数学问题链在教学改革中的文化基础问题，但关注得比较多的还是数学内部的思想、方法及其蕴含的教育价值，其主要从数学方法论的视角提出了数学问题链教学设计与实施的关键点[3]1，73-106。上述从文化的角度理解数学及数学教育的观点能进一步拓宽关于数学问题链教学的认识。

（一）体现数学与文化联系的多重性

笔者曾提出以数学关联为数学问题链教学设计与实施的逻辑起点，其主要包括三大关联，即表层信息关联、思考方法关联、思考视角关联。上述关联主要是基于数学学科内容、思想、方法的普遍联系并结合数学学习的相关理论提出来的，更多地体现了将“数学作为一个相对完整、独立的文化体系”这一维度的认识。因此，我们需要站在数学作为一个子文化和重要的文化力量的角度，进一步拓展对数学关联的认识，即认识到数学与更广泛的人类文化之间的普遍联系。因此，在教学中，教师一方面需要关注数学与文化传统之间的关系，使数学存在于更宏大的文化脉络中;另一方面需要关注数学与社会生活、科技发展以及学生的生活经验之间的联系。

（二）进一步彰显数学教育目标的文化性

从数学文化的角度来看，数学教学除了传承作为文化结果的数学知识，还要体现数学知识所存在的文化和发展的文化脉络，以及数学发展中人的主体创造性。这些在过去的数学问题链教学实践中也得到了广泛关注，比如通过问题脉络的设计，以体现数学知识发生发展的思维脉络;倡导为学生提供冷静思考与充分表达的机会来彰显学生在问题产生、知识建构上的主体性。当然，指向数学文化的数学问题链教学需要进一步彰显文化性，特别是需要关注数学问题链如何帮助学生理解数学及其发展的文化脉络，建立起数学与自身文化的意义关联，从而实现文化育人的目的。

（三）数學教学内容学科性与生活性的融合

数学文化融入数学教学的其中一个重要思路是“数学教学回归生活”。“数学教学回归生活”的核心是人的主体性回归，主体只有在用数学组织生活的同时建构数学，才能反映出数学真正的生活本质，也才能反映出数学发展中人的主体性[4]，只有这样才能避免教学中只见数学的背景而看不到数学发展的文化本质。当然这里的生活不能窄化为学生的日常生活，在时空上应该包括人类当下的生活、历史的生活甚至未来的生活，在生活领域上应该包括日常生活、社会生活乃至科学生活。问题链教学在内容上需将数学的学科性与学生乃至人类的生活加以融合，凸显问题链教学中问题的历史性、现实性。

二、数学问题链教学设计与实施的原则

指向数学文化的问题链教学除了应体现如目标指向的丰富性与高阶性、问题设置的真实性与适切性、问题使用的灵活性与深刻性、学习评价的伴随性等基本特征[3]55-63，还应遵循或者凸显以下原则。

（一）数学关联的多重性

指向数学文化的数学问题链教学除了需要关注数学的表层信息、思考方法、思考视角的关联，以体现数学内在整体结构与脉络，还需要建立起数学与文化、数学与社会、数学与人之间的广泛联系，使问题链中问题的产生、分析与解决具有文化之源、社会之根及人的心理经验之基。比如，随着大数据时代到来，人们越来越强调并适应定量思维的趋势，可以通过类似“如何刻画学生身高正常与否的定性描述”等问题建立起与正态分布等学习内容的联系。因此，需要从数学内外部对所存在的关联进行多重分析与选择，以此为问题链的设计提供基础。

（二）问题的境脉性

相对于一般的数学问题链教学，数学文化这一指向性要求体现问题，尤其是起点问题赖以存在的情境及情境发展的脉络，从而彰显问题的源头与思考的脉络性。诚然，数学中有一些问题确实是因为一时灵感而产生的，数学教学中也会有一些学生突然想到并提出一些非常有价值的问题，但一方面，从数量上来说这样的现象并不是普遍的、占大多数的，另一方面真正有质量的、顿悟式的提问往往也是在长时间的思考后产生的。因此，在教学中，教师应该让学生在有脉络的情境中产生疑问，并利用数学的思维分析问题、解决问题。这里的情境既可以是来自数学内部，也可以是来自数学外部的社会与文化。

（三）问题解决的实践性

数学文化强调人（类）在数学发展中的主体地位，而学科实践是在教学中体现人的主体地位的重要途径。问题链教学在实施过程中需要让学生成为问题解决的实践主体，让学生有机会分析问题，形成问题解决的思路与方法，同时经历新问题的衍生过程。

三、指向数学文化的问题链案例分析

（一）等腰三角形的关联分析

长期以来，人们认为数学是一门极具严密性的学科。而东西方的数学在其历史发展中都在一定程度上表现出由不那么严密的数学（有时还只是蕴含数学的经验）向严密的数学的发展过程。根据历史相似性原理，人们认识数学的过程与数学本身的发展过程具有相似性。这主要是指，学生学习数学的过程也需要经历由不那么严密的数学（或数学经验）向严密的数学发展的过程。依据上述思想，教师可以在“等腰三角形的性质”教学中，让学生观察生活中广泛存在的等腰三角形，以折纸为载体，经历“特殊几何关系驱动几何探索”“操作观察中形成猜想”“演绎推理中验证猜想”的数学严密化过程，感受数学的严密化精神[5]。

需要说明的是，无论在数学学习还是在数学本身的研究中，人们有时是在一个猜想后马上着手证明，有时又是一下子涌现出多个猜想之后才去逐个证明。从教学设计而言，如果为了更好地掌握知识，在一个猜想之后马上证明并应用也许会更好;但如果从数学活动的角度来说，特别是若干个猜想都基于同一个活动的情况下，就不一定非要按前一种思路进行。因为有时多个猜想会同时产生，如果硬是按“猜想—证明—应用”的逻辑，反而会使数学学习活动受到诸多的限制，抑制学生进一步探索的意愿。因此，在以下的案例呈现过程中采用的是第二种思路。

（二）教学过程

1.特殊几何关系驱动几何探索

寻找几何要素或几何对象间存在的特殊关系，进而以上述特殊关系为基础探索更多的几何性质，这是几何研究中的重要思路。在明确了等腰三角形是有两条边相等的本质属性后，学生便会自然地产生进一步探索的愿望，进而形成问题1。

问题1 生活中存在大量的如图1的等腰三角形。等腰三角形除了两边相等，还有哪些特殊几何关系？请观察手头的等腰三角形纸片，想一想可能存在怎样的几何关系，并折一折，从点、线段、角等几何元素间的关系角度进行讨论。

问题1提问方向较宽泛，其目的并非在于解决这一问题，而在于引发学生折纸等几何探索活动。该问题让学生从基本的几何元素出发，从而发现更多的几何关系。同时观察也为折纸提供了方向，即既可能会将两条相等的边折叠到一起，也可能会直观猜想两个底角也相等，进而尝试将两个底角折叠到一起。

2.操作观察中形成猜想

在几何学习中，折纸的目的是借助活动以及折纸而形成的折痕观察，发现可能存在的几何关系。因此，在问题1引发折纸活动基础上，可以引出更具体的问题2，并要求学生先独立观察再回答。

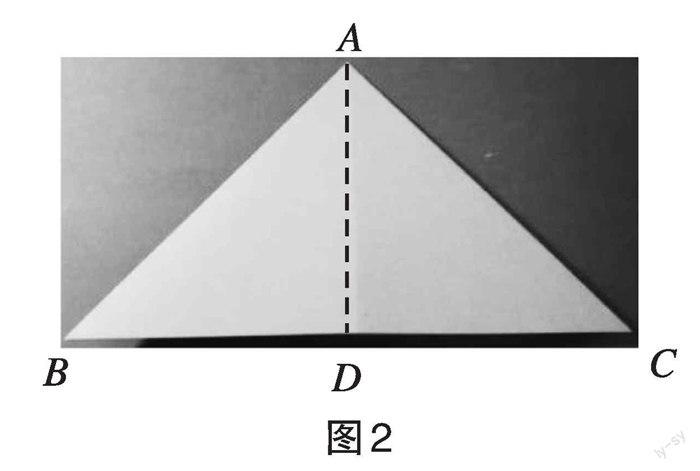
问题2 观察折叠并展开后的等腰三角形图形（如图2），在增加折痕后，你发现哪些几何关系？

学生通过观察能发现并形成以下猜想：（1）折痕AD将等腰三角形分成位于其两侧的两个全等的小三角形，由此得到等腰三角形ABC是一个轴对称图形，AD为对称轴;（2）点B和点C重合;（3）∠B和∠C重合;（4）∠BDA和∠CDA重合，即两个角均为直角，AD是在边BC上的高;（5）∠BAD和∠CAD重合，于是AD是∠BAC的角平分线;（6）BD与CD重合，于是AD是在边BC上的中线。由此至少可以得到3组角、1组线段的等量关系，以及等腰三角形的轴对称性，并通过进一步思考认识到AD既是底边上的高线、中线，也是顶角的角平分线。经归纳后，学生形成等腰三角形是轴对称图形、等腰三角形两底角相等、等腰三角形顶角角平分线、底边上的中线和高线三线合一的猜想。

在学生独立形成上述猜想的基础上，教师组织学生进行全班分享与讨论，使个人的猜想公开化，这也是进一步用更多的操作、观察、验证、猜想的过程。这一方面使获得的数学猜想得到强化，对猜想的描述变得更加清晰，另一方面也为学生体会证明的必要性提供铺垫。

为了进一步强化猜想，还可以借助几何画板进行更深入的几何实验。即先根据定义画出一个等腰三角形，再利用几何画板中的度量功能对所绘制的等腰三角形中的几何量进行测量，验证上述猜想中存在的等量关系及相应的猜想。

有研究显示，初中学生的抽象逻辑思维正处于从经验型向理论型的过渡时期，学习几何时还需较多地借助直观操作[6]33-36。因此，在上述学习活动中，应强调以折纸以及观察带有折痕的等腰三角形纸片等操作性的活动为基础，即使是借助几何画板的验证也仍然是操作性的，从本质上来说属于几何實验的范畴。

3.演绎推理中验证猜想

演绎推理既是数学严密化精神的集中体现，也是数学大厦屹立不倒的重要原因。通过操作、实验获得的几何结论还存在较强的经验性和易谬性，在数学上还无法令人完全满意。后者事实上就是数学严密化精神的重要作用。反过来，操作性的、几何实验的活动及以此为基础形成的几何猜想也为几何证明提供了基础。这种基础既是认知层面的，也是心理层面的。由实验几何引起的证明欲望，或者对证明必要性的体验往往会更强烈[6]33-36。因此，在教学中，教师需要通过问题引发学生对操作性实践中形成猜想的不确定性的感受，进而将学生自然地引向演绎推理式的证明活动中。

由以上的操作活动，学生获得了三个猜想，但这些猜想都只是从操作、观察中获得的，尽管已经经过了验证，但在数学逻辑上还是不能令人满意的。那么，怎样才能使得到的结论更具有说服力呢？

教师在与学生一起回顾数学中通过证明增强说服力的方法后，便自然产生了对猜想进行证明的问题。由于只靠“两边相等”这个条件还无法展开更多的讨论，因此需要增加一个条件。教师可以引导学生观察折痕的特点，并任选其中一个作为先决条件。当然，根据前述折叠的方法，这里将折痕作为底边上的中线会更加自然，因为要将两条相等的边叠到一起，就是要将点B和点C重叠到一起，于是就有BD=CD。这时需要证明以下问题3。

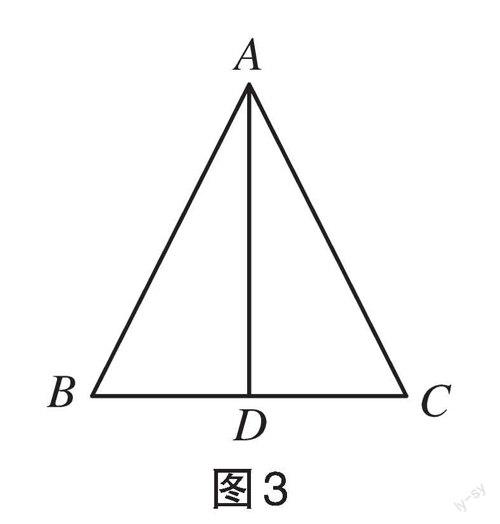
问题3 如图3，等腰三角形ABC中，已知AB=AC，BD=CD。求证：（1）三角形ABC是轴对称图形，且AD为对称轴;（2）两底角相等;（3）底边上三线合一。

这个证明本身是比较简单而直接的，即通过“边边边”这一三角形全等的判定定理即可得到[ABD?ACD]，于是问题3的三个小问得到证明。

在教学中，教师还可以和学生讨论上述证明中增加的条件的可变性，即将顶角角平分线或底边上的高线作为先决条件再进行证明。这里还可以适时地引入历史上如帕普斯借助顶角角平分线给出的证明方法等，使学生有机会体验到数学的历史厚重感。

4.历史中感受等腰三角形

无论是中国古代还是西方，等腰三角形都早已被人们发现，其性质也得到了广泛的应用。比如中西方都利用等腰三角形中的三线合一定理制作了水准仪。有意识地挖掘这些文化素材，并做教育学的转化，既可以让学生更深入地理解、应用知识，达到掌握知识的目的，同时也可以让学生感受到数学在人类文化发展中做出的重要贡献，体会数学作为一种文化力量的存在。基于这個目的，可以设计以下问题4。

问题4 图4是一个古罗马墓碑上的图案，其中墓碑顶上是一个等腰三角形和一条铅垂线;图5是我国古代建筑工人的水准仪，用一把等腰三角形尺和悬挂在顶点处的铅锤线来检查横梁是否水平。你能说一说，这些水准仪为什么能够测定横梁是否水平？

以上是从数学文化的角度进一步拓展对数学问题链教学的认识，初步给出了指向数学文化的数学问题链教学需要进一步关注的原则，并尝试通过一个案例初步加以说明，未来还需要进一步讨论指向数学文化的问题链教学的设计与实施策略。

参考文献：

[1]唐恒钧.数学文化的教学意蕴及问题链的价值[J].中小学课堂教学研究，2022（7）：4-7.

[2]喻平.发展学生学科核心素养的教学目标与策略[J].课程?教材?教法，2017（1）：48-53，68.

[3]唐恒钧，张维忠.数学问题链教学的理论与实践[M].上海：华东师范大学出版社，2021.

[4]陈碧芬，张维忠，唐恒钧.“数学教学回归生活”：回顾与反思[J].全球教育展望，2012（1）：86-92.

[5]米山国藏.数学的精神、思想和方法[M].毛中正，吴素华，译.上海：华东师范大学出版社，2019.

[6]唐恒钧.案例的视角：几何实验与几何证明[J].中学数学杂志，2005（8）：33-36.

（责任编辑：陆顺演）