初中数学解题教学五部曲刍议

杨周荣麟

[摘  要] 文章从一道期末压轴题的说题过程说起，谈谈解题教学的五部曲，以推动学生的思维发展，促进学生的素养生成.

[关键词] 解题教学;五部曲

解题教学是数学教学的重要组成部分，可以分为审题——分析——解答——拓展——整理五个步骤[1]. 作为一种新型的教研形式，说题活动映射出教师对于解题教学的理解与把控，它受到了越来越多的重视. 笔者结合一次说题教学，谈谈解题教学的五部曲，意在抛砖引玉，与大家共勉.

原题再现

如图1所示，若二次函数y=-x2+3x+4的图像与x轴交于点A、B，与y轴交于点C，连接AC，BC.

（1）求△ABC的面积;

（2）若P是抛物线在第一象限内BC上方一动点，连接PB，PC，是否存在点P，使四边形ABPC的面积为18，若存在，求出点P的坐标;若不存在，说明理由;

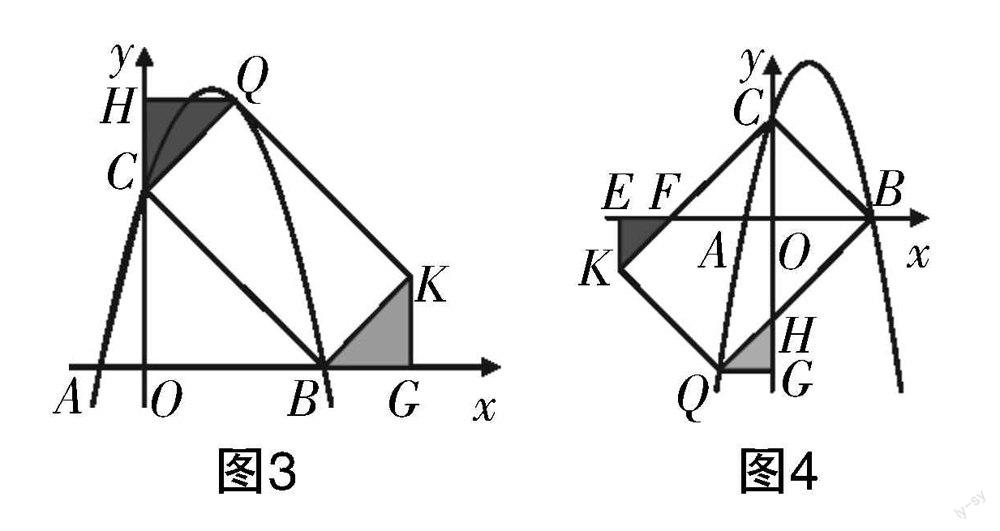
（3）如图2所示，若Q是抛物线上一动点，在平面内是否存在点K，使以点B，C，Q，K为顶点，BC为边的四边形是矩形？若存在，请直接写出点K的坐标.

试题分析

这是期末试卷的最后一道压轴题，综合性强，难度大，对学生的思维能力要求比较高，考查了二次函数的图像与性质、一元二次方程的解法、矩形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质等数学知识，渗透了数形结合思想、分类讨论思想、方程与函数思想、转化与化归思想、数学建模思想等，要求学生能根据题意建立一元二次方程的模型，发现并构建等腰直角三角形的模型、全等模型等，从而解决问题.

说题呈现

第一步：审题，正确解读题意，找出关键词.

画一画：二次函数y=-x2+3x+4，A，B是抛物线与x轴的交点，C是抛物线与y轴的交点，这三个点都是定点. 第二小题的P是动点，它被限定在第一象限的抛物线上，在BC的上方. 第三小题的Q、K也是动点，点Q在抛物线上，点K在平面内，随点Q的确定而确定. 试题重点考查抛物线与三角形交汇问题，抛物线与矩形交汇问题.

在解题教学中，学生要养成良好的、正确的审题习惯，离不开教师的引导. 提高学生的审题能力，需要让学生在读题的过程中画出关键词，从而获取有价值的信息，有了良好的审题习惯，等于成功了一半.

第二步：分析，找出突破口，明确解题思路.

想一想：（1）根据三角形面积计算公式，欲求△ABC的面积，需要求出它的底边AB与高OC的长，欲得到线段OC，AB的长，只需求出这三点的坐标即可. （2）观察图1，因为四边形ABPC的面积为18，△ABC的面积也已确定，所以△PBC的面积确定. 如何求点P的坐标？点P在抛物线y=-x2+3x+4上，所以它的横、纵坐标满足函数关系式，只需求出点P的横坐标即可，此时可根据△PBC的面积建立关于点P横坐标的方程，通过解方程求得点P的坐标.

画一画：（3）以点B，C，Q，K为顶点，BC为边的四边形是矩形是否存在？首先应根据题意画出草图，当点Q在y轴右侧时，如图3所示，当点Q在y轴左侧时，如图4所示. 当点Q在y轴右侧时，为求点Q的坐标，需要按横平竖直的原则，作坐标轴的垂线，从而构建全等三角形，利用全等三角形转移线段长，从而求得点K的坐标. 当点Q在y轴左侧时同理.

在分析题意的过程中，教师设置了两个环节，一是想一想，通过关键词找到解决问题的突破口;二是画一画，根据题意，画出符合题意的图形，捋出正确的解题思路，为解决问题搭好框架. 需要注意的是，画图形时，教师不能直接把图形出示给学生，要让学生根据题意自行画出图形，然后在小组内交流讨论.

第三步：解答，作出辅助线，算出正确结果.

添一添：对于第（2）小题，△PBC是一个倾斜的三角形，如何切分能利用顶点的坐标表达线段的长呢？这里有两种基本的方法，即过点P作竖直线，或过点C作水平线. 对于第（3）小题，为了求得点Q或点K的坐标，仍需要添加横平竖直的直线，作辅助线的方法如图3、图4所示.

解一解：（1）对于抛物线y=-x2+3x+4，当x=0时，y=4，所以C（0，4），当y=0时，即-x2+3x+4=0，解得x1=4，x2=-1，所以A（-1，0），B（4，0）. 所以AB=5. 因为OC⊥AB，所以S△ABC=×5×4=10.

（2）存在符合题意的点P，理由：因为四边形ABPC的面积为18，S△ABC=10，所以△BCP的面积为8. 因为直线BC经过点B（4，0），点C（0，4），根据待定系数法，得直线BC的解析式为y=-x+4，如图2所示，过P点作PM⊥x轴，交BC于点M，因为点P在抛物线y=-x2+3x+4上，所以设P（t，-t2+3t+4）. 因为PM⊥x轴，点M在直线y=-x+4上，所以点M（t，-t+4），根据坐标系中利用三角形面积计算宽高的公式，得S△BCP=×4×PM=2（-t2+3t+4+t-4）=2（-t2+4t）=8，解得t=2，所以P（2，6）.

（3）存在符合题意的点K. 理由：设点Q（m，-m2+3m+4），当m>0时，如图3所示，因为四边形CBKQ是矩形，所以QK∥BC，CQ⊥BC，KB⊥BC. 过点Q作QH⊥y轴，交于点H，过点K作KG⊥x轴，交于点G. 因为△OBC是等腰直角三角形，所以∠OCB=∠OBC=45°. 所以∠HCQ=∠GBK=45°. 因为CQ=BK，根据“角角边”，得△CHQ≌△BGK，所以CH=HQ=BG=GK. 所以m=-m2+3m+4-4. 解得m=2或m=0（舍去）. 所以HQ=CH=2. 所以BG=KG=2. 因为OB=4，所以OG=6，K（6，2）;当m<0时，如图4所示，因为四边形CBQK是矩形，所以QK∥BC，KC⊥BC，BQ⊥BC，设KC与x轴的交点为F，BQ与y轴的交点为H，过点Q作QG⊥y轴，交点为G，过点K作KE⊥x轴，交点为E. 因为△OBC是等腰直角三角形，所以∠OCB=∠OBC=45°. 所以△FBC、△BCH也是等腰直角三角形. 所以∠OBH=∠OHB=45°，∠FCO=∠CFO=45°，OF=OC=OB=OH=4. 所以∠HQG=∠EFK=45°. 因为KC=BQ，CF=HB=BC，所以FK=QH，根据“角角边”，得△QHG≌△KFE，所以QG=HG=FE=KE，所以-m=-4-（-m2+3m+4），解得m1=-2，m2=4（舍去）. 所以QG=HG=FE=KE=2. 因為OF=4，所以OE=6. 所以此时点K的坐标为（-6，-2）. 因此点K的坐标为（-6，-2）或（6，2）.

分析题意为解答问题做了很好的铺垫，教师引导学生添加适当的辅助线，把倾斜的三角形分为两个三角形，从而能利用公式求三角形的面积;教师引导学生借助三垂直模型与全等三角形模型，一元二次方程模型求得了点Q的横坐标，从而求得了点K的坐标，使学生体会到数学建模在解决数学问题中的重要性;教师从学生的最近发展区出发，根据学生的认知规律，引导学生发现最易想到的解决方案，突破了难点.

第四步：拓展，寻找延伸点，让学生思维生长.

变一变：如图1所示，若二次函数y=-x2+3x+4的图像与x轴交于点A和点B，与y轴交于点C，连接AC，BC.

（1）若P是抛物线在第一象限内BC上方一动点，连接PB，PC，当△PBC面积最大时，求点P的坐标.

（2）已知M是平面内一点，是否存在以点A，B，C，M为顶点的平行四边形，若存在，求出点M的坐标.

（3）若P是抛物线在一象限内BC上方一动点，过点P作PH⊥BC，是否存在点P，使得△PCH与△OBC相似？

教师对原题进行恰当的变式，在改编时没有改变原题的背景，只是把“当△PBC面积为固定值”改变为“当△PBC面积为最大值”，此时学生需要建立二次函数的模型，根据二次函数的最值性质求解. 把“以BC为边构造矩形”改变为“以A，B，C三点为顶点构造平行四边形”，此時学生需要分三种情况讨论，培养了学生思维的发散性与融合性，提高了思维的深度.

第五步：反思，梳理思维脉络，积累解题模式.

理一理：请大家回顾解题过程，你们在其中用到了哪些数学知识？学到了哪些解题技能？又学了哪些数学思想？它们是如何联系在一起的？

画一画：把上述的解题反思形成一张思维导图. 从数的角度看，本题考查了二次函数、一次函数、一元二次方程;从形的角度看，本题考查了二次函数的图像，矩形、等腰直角三角形、相似三角形、全等三角形.

解题反思是解题教学的收官之笔，其重要性不言而喻，有利于学生总结经验形成方法，进而实现知识的触类旁通、举一反三[2].

结束语

关于解题教学的五个步骤，相辅相成，浑然天成. 在实际教学中，教师也可以根据需要删增某一步骤，有针对性地做出设计，以推动学生的思维发展，促进学生的素养生成.

参考文献：

[1]庙军生. 说题在初中数学教学中的应用[J]. 中学教学参考，2020（30）：55-56.

[2]李慧敏. 关注数学解题过程——从解题规范的视角谈解题教学[J]. 中学数学月刊，2019（03）：58-59.