让复习成为学习能力提升的“金钥匙”

黄克铜

[摘  要] 为了提升复习效果，在复习时教师可以变换基础知识的呈现方式，通过练习、反思、拓展创新等方式让学生更好地认识知识、认识自己，提升学生总结归纳的能力以及分析和解决问题的能力，以此培养学生良好的学习习惯和数学素养.

[关键词] 复习;能力;素养

复习课看似简单，然而要上好却很难. 有的教师收集和整理大量的易错题、重点题，把复习课上成了习题课;有的教师引导学生将简单的知识梳理后让其如机械般重复练习书本中的习题，使复习课变成了“炒冷饭”课;有的教师带领学生一直重复“练习—校对—再练习—再校对”的模式，试图让每个学生把每道题都能做到既懂又会;还有的教师将复习课变成了答疑课，由学生自由发问，师生互动答疑，课堂看似生动活泼，却没有完成复习课巩固知识、实现拓展创新的目标. 因此，笔者结合自己的教学经验，谈谈如何上好一节复习课.

借“题”发挥

数学习题在数学课堂是必不可少的，恰当的习题练习可以有效地避免单一的知识梳理所带来的枯燥感. 当然，这里所指的习题练习并不是“题海战术”，而是引导学生通过解题回忆习题中所涉及的基础知识和基本技能，实现“双基”的巩固. 为了实现这一教学目标，教师在习题的选择上应做到精挑细选，既要有针对性，又要兼顾全面，让学生完成由实践到理论的提升.

以“有理数”的复习课为例，如果让学生用精准的数学语言表述相关的概念，学生会感觉很困难，而让学生直接完成相应的练习，学生往往会得心应手. 因此，教师可以采用习题练习的方式引导学生复习该知识点.

（1）正数和负数

例1：+3，-2，3.1415，-201，-（+19），+123.

正数是_______，负数是_______，分数是______，有理数是______.

（2）数轴

例2：下图中，表示数轴的是（  ）

（3）相反数

例3：下列说法正确的是（  ）

①-5是相反数;②-5与+3互为相反数;③-5是5的相反数;④-3与3互为相反数;⑤0的相反数是0.

A. ①②B. ②③⑤

C. ③④⑤ D. ①④⑤

（4）绝对值

例4：若a=-a，则a是（  ）

A. 0 B. 正数

C. 负数 D. 负数或0

例1主要考查的是学生对有理数相关概念的掌握情况，通过练习让各概念呈现得更加直观，有利于帮助学生理解有理数相关概念之间的区别和联系;例2主要考查的是学生对数轴三要素的掌握情况，在本题的探究中，教师可以引导学生“说一说其他图形不是数轴的原因”，进而让学生体验条件中的“缺一不可”;例3和例4分别从正确和错误两个不同的方向反映了相关概念的意义，这样通过正反两个角度进行思考，有利于加深学生对相关知识点的理解，实现“理论—实践—理论”的升华. 对于例2、例3、例4，因为其是以选择题的方式呈现的，所以有些学生得出正确答案可能应用的是小技巧. 因此，为了更好地知道学生的实际掌握情况并制订相关的复习计划，教师可以指定一些基础薄弱的学生来“说一说”，听听他们是如何理解问题的，通过有效引导帮助学生将基础知识吃透、夯实，从而为后面的代数复习奠定坚实的基础.

借“思”提升

在复习课上教师要充分发挥反思的力量，通过反思错题，让学生找到易错点和自己的薄弱点;通过反思知識点之间的关联性，让学生理清数学知识脉络，建构完善的知识体系;通过反思重难点，让学生把握核心考点，找到解题的突破口. 这样的反思有利于学生对自我知识结构和认知水平形成更全面的、系统化的认识. 在此环节，教师可以安排一些变式练习或综合性练习，进而让学生在已经掌握或理解的知识点上有所突破，找到知识点之间的融合点、融合方法和融合形式，以此提升学生解决实际问题的能力，进而提升解题信心.

例如复习“三角形”时，教师可以从边、角、线三方面入手，若能将其完美地融合起来，可以有效地实现知识的纵向延伸和横向拓展，通过纵横交织形成完整的认知体系，提升学生的知识迁移能力和思维的灵活性.

例5：已知△ABC的两边长分别为3，4，那么第三边长可能是（  ）

A. 1B. 5 C. 7D. 9

评析 本题为基础题，很多学生在解题时都应用了小学阶段学习并掌握的“三角形的三边关系”，这是利用知识迁移解决问题的过程：已知两边长分别为3，4，联想到第三边长为5. 这样利用一个简单的、基础的问题就复习了两个知识点，既让学生实现了知识的巩固，又使学生解决问题的能力逐渐向多样化和简单化过渡.

例6：已知△ABC的两条边AB和BC的长分别为4和6，AB，BC，CA各边的中点分别为D，E，F，那么△DEF的周长可能是________.

评析 例6不仅考查了“三角形的三边关系”，还与三角形中位线定理紧密相连，通过巧妙融合提升了问题的灵活性，考查了学生对基础知识的掌握情况.

例7：小刚有两根长度分别为4 cm和10 cm的木棍，他想再找一根木棍拼成一个三角形的相框. 现在有图1所示的5根木棍可供选择，若任选其中一根，你能算一算他能够拼成三角形相框的概率吗？

评析 本题将“三角形的三边关系”与“概率”相融合，考查了学生数学思维的全面性和严谨性，同时借助生活实际问题更易于激发学生探究的热情.

例8：若△ABC的边长均满足方程x2-6x+8=0，则△ABC的周长是_______.

评析 三角形的三边是通过方程的形式给出来的，△ABC为等腰三角形这一信息隐藏于题设中，使问题更具探究性.

例6、例7、例8三个问题均与其他知识相融合，如例6中的中位线定理，例7中的概率，例8中的方程，通过巧妙融合不仅达到了帮助学生巩固三角形三边关系的目的，而且让学生找到了该知识与其他知识的融合点，使数学问题变得丰富多彩，有效地培养了学生数学思维的灵活性和变通性，提升了学生的知识综合运用能力.

在练习题的设计上，教师要多关注问题的灵活性、多样性，借助问题帮助学生巩固“双基”的同时，通过合理的变式将不同的知识点进行串联，通过反思、总结帮助学生建构完善的认知结构，提升学生的数学综合运用水平.

借“题”创新

创新是学习的最终价值所在，通过前面的复习，学生已经具备了扎实的基础以及分析和解决一般性问题的能力，为创新奠定了坚实的基础. 在该环节的习题选择上，教师既要重视与前面两个环节的沟通，引导学生联系基础知识和基本方法，又要兼顾综合和创新，培养学生独立思考问题的能力. 只有让学生学会独立思考，自主发现数学规律，认清问题的本质，才能拥有创新的技能.

例如复习“平行四边形的判定”时，教师可以先组织学生动手“画一画”，复习巩固相关的判定方法，接下来借助一些梯度问题实现拓展和延伸.

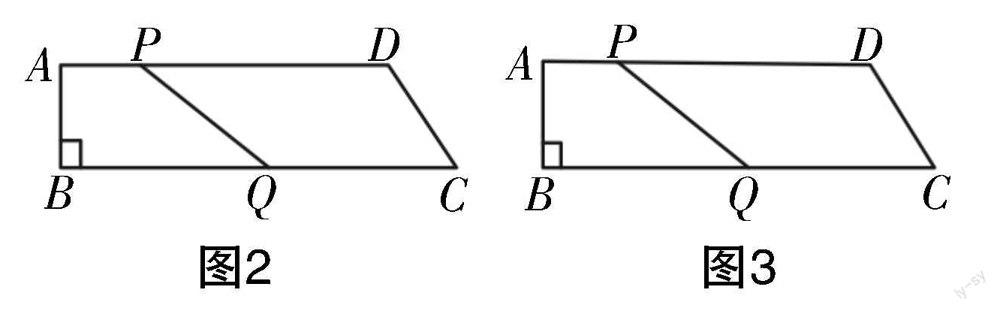
例9：如图2所示，四边形ABCD为直角梯形，∠B=90°，AB=8 cm，AD=24 cm，BC=26 cm，Q为BC的中点，点P为AD上任意一点，当AP=________时，四边形PQCD为平行四边形.

例10：如图3所示，四边形ABCD为直角梯形，∠B=90°，AB=8 cm，AD=24 cm，BC=26 cm，动点P和动点Q分别从A点和C点同时出发，点P以1 m/s的速度向点D移动，点Q以3 m/s的速度向点B移动，点P或点Q无论哪个动点到达端点，另外一个动点都会停止运动. 请问经过多长时间，可以使四边形PQCD变成平行四边形？

例9看似动点问题，实则是定值问题，借助定值引导学生应用平行四边形的判定方法解决问题，能实现知识的巩固，加深学生对相关性质、定理的理解，同时为接下来探究例10的动点问题做好充足的準备. 例10的难度虽然略有提升，但有了前面问题的铺垫，大多数学生还是能够顺利求解.

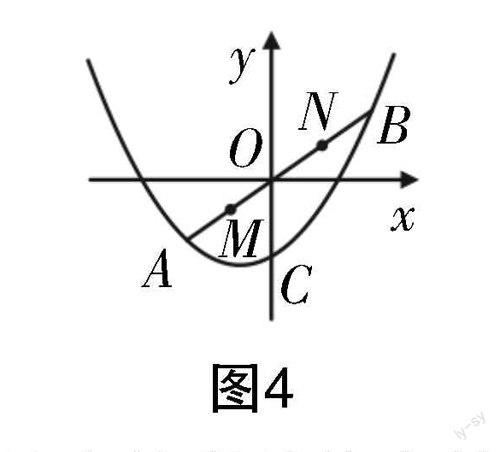
例11：抛物线y=ax2+bx+c与y轴相交于点C（0，-2），与直线y=x相交于点A（-2，-2），B（2，2）.

（1）求抛物线的解析式;

（2）如图4所示，线段MN=，其在线段AB上移动，且点M与点A不重合，点N与点B不重合，若点M的横坐标为m，过点M作x轴的垂线相交于点P，过点N作x轴的垂线相交于点Q. 请问点P，M，Q，N是否可以围成一个平行四边形？若能，请求出m的值;若不能，请说明理由.

本题具有较强的综合性，以前面两个例题为基础，又添加了函数思想和分类思想，具有一定的难度，但有了前面两个例题的铺垫，学生易于找到解题的突破口. 这样通过层次性问题的设计，有效地化解了问题的难度，让学生都能参与解题的过程，并能够有所发展. 同时，通过层次性问题的铺垫，可有效消除学生的畏难情绪，让学生知道其实综合题都是由简单的题目综合而来的，只要通过逐层分析，定能找到合理的解题突破口，进而提升学生的学习信心.

总之，复习不是简单的知识罗列，教师必须结合实际水平和知识结构特点精心设计复习流程，既要关注“双基”的巩固，又要有所提升、有所创新，进而培养学生的数学学习信心，提高学生的综合能力.