灵活应用课堂生成 优化学生数学认知
2022-05-30翟芳
翟芳


[摘 要] 为了使数学课堂更具生命力,教师应注意课堂生成性资源的开发与利用。在教学中教师应多鼓励学生去质疑、去观察、去联想、去探究,从而引发学生深度思考,培养学生良好的思维习惯和学习习惯,以此提高学生的数学学习能力。
[关键词] 生成性资源;思维习惯;学习能力
随着新课改的不断深入,数学课堂也呈现出了新气象,“预设”与“生成”已成为数学课堂的重要组成部分。为了更好地完成教学,大多教师会结合学情对教学内容进行充分的预设,进而便于学生更好地参与课堂,发挥学生的主体作用。不过虽然教师课前做好了充分预设,但是在面对学生的奇思妙想时,不少教师还是有些力不从心,不能很好地利用这些生成性资源开展更有效的教学活动。因此,对于如何捕捉生成性资源,使之成为课堂新的生长点,依然是值得教师关注的课题。对于如何发现、如何捕捉,笔者谈了几点自己的认识,仅供参考!
一、在质疑中捕捉
数学课堂是动态变化的,即使课前教师做了充分的预设,在课堂中也会出现一些小“意外”,这就要求教师作为课堂的组织者,应及时地捕捉“意外”,并鼓励学生对这些“意外”再“探一探”,进而让学生在释疑的过程中更好地理解新知,建构认知,获得数学理解。
例1 图形的平移
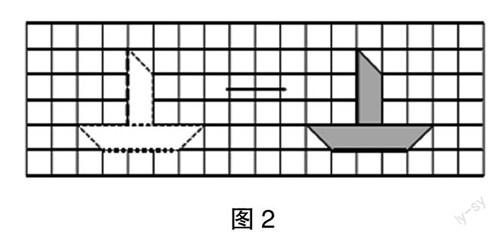
师:观察图1,你知道小船向什么方向移动了吗?(教师PPT展示图1,并给出问题引导学生观察)
生(齐声答):向右移动。
师:你们个个都很棒。现在数一数,它移动了几个格子呢?(教师给学生足够时间让学生认真观察)
生1:移动了4个格子。
生2:不对,移动了9个格子。
师:哦,看来大家有了不同的意见,那么到底是生1说得对,还是生2说得对呢?
师:现在大家拿出我们的作文本,将其中一个格子描上红色,假如将这个红色格子移动向右移动一格会是什么效果呢?(学生很快就有了结果)
师:现在大家再动手画一画看看移动4个格子和9个格子又会是什么样呢?(通过动手做学生轻松地解决了问题)
师:现在我们再看看小船,你是否有答案了呢?
生(齐声答):是移动了9个格子。
师:很好,这次大家的答案都对了,那么谁能具体地说一说,你是怎么得到答案的呢?
生3:我是数对应边移动的格子。(学生在PPT上指出了如图2所示的一组对应边)
师:那么大家按照生3的说法数一数,看看小船向右平移了几个格子呢?
生(齐声答):9个。
师:除了对应边,还可以看什么呢?
生(齐声答):对应点。
师:很好,如图3,大家按照对应点数一数,看看是不是9个格子呢?
生(齐声答):是9个格子。
师:以后如果遇到平移多少格子的问题时,我们可以用什么方法数呢?
生4:找准对应边或对应点。
在案例1的教学过程中,学生通过动手做、用眼看、用心悟,理解并掌握了方法。从最终的课堂反馈来看,学生较好地完成了教学目标,对“平移几个格子”有了深刻的认识,达到了预期的效果。不过若仔细思考整个过程会发现,在后期探究过程中,教师忽视了对错误资源的开发和利用。有时候若对学生的质疑不进行及时引导,错误的意识会不断生长,最终会影响后期的应用。在例1探究过程中,教师应对给出“平移4格”这一结果进行一个正面的评价,并给予适当的引导。例如,教师可以进行追问:你认为是平移了4格,看来是深思熟虑,认真探究的结果,那么能不能说一说你是怎么想的呢?为了能够让别人认同自己的观点,学生会仔细思考,认真组织语言,以使表达更具说服力,这样可以有效地锻炼学生的表达能力。同时在交流过程中,可以充分暴露学生的思维过程,进而便于教师找到问题的症结,便于课上进行有效的引导和修补,从而提高学生解决问题的能力。
在数学教学过程中,教师不应将目光单纯地放在知识和技能上,要注意学生自我发现、自主探究能力的培养。同时,教学中也要引导学生树立正确的学习观,既不要因为出现错误而焦虑,也不要因为得出正确的结果而沾沾自喜,要培养学生敢于面对挫折的勇气,这对现代教育来讲是不可或缺的。
总之,在教学过程中,教师要善于捕捉课堂生成性资源,对那些存在分歧、存在疑问的问题,教師可以引导学生进行再思考,从而让学生可以自觉地进入更深层的探究活动中,这样既能实现自我释疑,又能更加全面地认识新知,对学习能力的提升是至关重要的。
二、在观察中发现
动手“做”是小学生获取数学知识最有效、最直接的数学活动之一。通过“做中看”可有效提升学生的直觉思维能力,加之教师精心设计和科学指导,可以诱发学生深度思考。通过这样动手“做”,学生不仅可以体验数学学习的乐趣,也能在思考中有所收获、有所成长。
例2 围三角形
课前准备:将班级学生分为8组,每组准备以下长度的小棒各1根:4cm,5cm,6cm,10cm。
师:课前我们已经进行了分组,并安排组长准备素材,各个小组都准备好了吗?
生(齐声答):准备好了。
师:大家都很棒。现在各个小组试一试,看看用这些小棒能够围成三角形吗?如果可以,共有几种围法呢?(教师的问题给出后,各个小组积极实验,很快给出了答案)
生1:可以用4cm,6cm和10cm这3根小棒围出一个三角形。
生2:不可能,我们小组刚刚也试过了,根本围不出来。
师:那我们就让生1给大家展示一下。(教师投影展示生1的结果,如图4)
生1:你们看,这个不是三角形吗?(生1露出了得意的笑容)
师:看上去确实是一个三角形,不过大家仔细想想,4cm和6cm这2根小棒接起来正好等于10cm,它们首尾相接会出现什么情况呢?是三角形吗?
生1:确实不能,3根小棒应该是重叠在一起的,那么刚刚为什么我们动手做的时候确实围成了呢?
师:其实刚刚大家看到的效果是因为误差所致,为了避免误差,我们在电脑上演示一下。
教师演示围成过程,学生通过观察发现,正如生1所说,3根小棒重叠在一起了。接下來又做了其他尝试,从而得到了4cm,5cm,6cm和5cm,6cm,10cm这两组小棒可以围成三角形,接下来教师带领学生继续探究,从而得出三角形的三边关系。
相信以上过程教师并不陌生,在日常教学中大多教师都是采用这个的方法开展教学的。确实,此过程既通过动手实验调动了学生积极性,又应用了现代信息技术生动了课堂,最终让学生总结归纳出了“三角形三边关系”这一重要内容,整个过程看似无懈可击。但有一点值得注意,就是在解释4cm,6cm,10cm这3根小棒不能围成三角形时,教师指出是误差影响了效果,又通过多媒体技术进行有效的补充,可对于小学生来讲,其很难理解误差,即使学生最终知道了答案,接受的过程也不是愉悦的。那么除了利用误差解释就没有其他的方法让学生去理解了吗?基于此,笔者做了以下尝试。
例3 探究不围的秘密
课前准备:各组准备以下长度的小棒各1根:4cm,5cm,8cm,10cm。
师:请各小组讨论一下,看看什么情况能够围成三角形,什么情况下不能呢?
学生操作,教师巡视。各个小组有着明确的分工,有的学生负责动手操作,有的学生负责记录,很快就统计出了结果。
师:根据大家的统计结果发现,4cm,5cm,10cm这3根小棒不能围,谁能具体地说一下原因呢?
生1:因为4cm和5cm太短了。
生2:是的,2根加起来还没有10cm的那根长。
师:哦,原来是太短了,那么可不可以加长一点呢?我们就将5cm那根加长,你们认为可行吗?(教师演示围成过程)
生3:可行是可行,不过也要加到足够长,如果只加0.5cm还是不够长。
师:确实,刚刚加了0.5cm还是不够长。(教师再次演示围成过程)
教师一边演示过程一边提问,如果我们加到6cm是不是就够长了呢?
生4:还不够长,如果加6cm只能让它们一样长,应该再长一点。
师:再长一点是怎么理解的呢?
生5:就是2根加起来要比10cm的那根长一些。从演示过程可以看出,只要比10cm长一点,那2根就拱起来了,就能构成三角形了。
师:拱起来了,很生动、很形象,大家都能理解吗?(学生纷纷点头表示已理解)
以上过程可以看出,教师在长度的设计上是经过深思熟虑的,因为对于两边之和等于第三边的验证,有时候因为误差会让学生产生错觉,为此教师要规避因为误差可能造成的错误结论,通过另辟蹊径帮助学生解决教学重难点,突破认知冲突。在教学过程中,教师以4cm,5cm,10cm这3根小棒不能围成三角形为例,通过由短变长的过程让学生发现若加得不够长仍然不能围成三角形,这就使得学生会重点关注那个临界值,即相等,从而自然地得出了两边之和与第三边的关系。当然,在教学过程中,多媒体技术的优势一览无余,学生通过直观观察和切身感受发现了如何让两边“拱起来”的秘密,通过探究完成了新知的建构。
总之,在数学教学中,教师应注重培养学生的观察能力和探究能力,进而让学生的认知在观察和想象中逐渐得到完善,学习能力逐渐提升。
