真三轴状态下煤岩单体的强度变形特性及破坏模式研究

2022-05-30刘子硕韩立军朱合轩

金属矿山 2022年5期

刘子硕韩立军朱合轩

(1.中国矿业大学力学与土木工程学院,江苏徐州 221116;2.深部岩土力学与地下工程国家重点实验室,江苏徐州 221116)

随着浅部煤炭资源日益枯竭,我国的煤炭开采深度不断加大,深部开采将成为煤炭资源开发中的常态[1],而深部“三高一扰动”的复杂力学环境也为深部开采带来了诸多难题和挑战[2]。软岩、强采动、大变形是我国煤矿巷道的主要特征[3]。煤层开采后,自巷顶至地面的所有上覆岩层均会受到不同程度的采动影响[4]。针对巷道直顶具有的煤—岩层状结构,对煤岩单体开展强度变形等相关研究,对深部巷道围岩控制技术研发与应用有着重要指导意义。基于煤岩体的强度变形特征对深部巷道稳定控制的重要性,国内许多学者开展了一系列研究。文献[5-7]研究了煤岩单体和煤岩组合体在不同轴向荷载或围压作用下的力学特性、冲击倾向性特征以及破坏机理。文献[8-9]基于煤岩的层理方向效应,开展了一系列的试验研究。文献[10]通过对煤样开展岩石力学试验,验证了煤样的单轴抗压强度、抗拉强度和点荷载强度的关联性。文献[11]对巷道的顶底板岩石开展了点荷载强度与抗压强度对比试验研究。文献[12-13]则对循环荷载作用下煤岩体的强度变形及渗透性等特征进行了研究。受到试验条件等限制,以上研究大都基于单轴或常规三轴试验,但煤岩体受到赋存情况、煤层倾角等地质条件的限制以及地应力的影响而有明显差别,所处的应力条件一般为三向不等压状态[14-15]。由于地应力分布情况极其复杂,在某些情况下,三向应力的差异可能很大,因此简单的加载条件不能代替实际复杂的地应力条件[16]。真三轴试验通过分别控制3个方向的加载过程,其试验结果更具有实际参考意义。国内已有学者通过真三轴试验对煤岩体性质进行了深入研究,但主要集中在瓦斯渗流[17-18]、高地应力下的岩爆[19]或煤爆现象[20]等方面,现阶段有关真三轴条件下针对原位煤、岩强度变形特征的对比试验研究比较薄弱。本研究以山西华晋韩咀煤矿为工程背景,通过分别对煤和岩石相似材料开展真三轴加载试验,分析两者的强度及变形特征,为相关理论研究及工程实践提供参考。

1 试验方法

1.1 试样制备

试验所用的煤样取自山西华晋韩咀煤矿32101主运顺槽,地面标高为+790～+920 m,井下标高为+570～+615 m。巷道所在煤层平均厚度为5.8 m,2#煤呈黑色,条痕为黑—灰黑色,玻璃—金刚光泽。半暗煤裂隙不发育,质地坚硬;亮煤裂隙发育,性脆、质轻、很易破碎,有时可见正交节理。试验所用煤样为现场取芯,并按照岩石力学试验规程对试样进行加工。

煤层顶板多为粉砂岩,灰黑色,性脆,胶结较好。根据项目钻孔勘察结果及相关地质资料,粉砂岩的相关物理力学参数取值见表1。由于项目实施尚处于初期阶段,顶板岩体钻取、加工及打磨较为困难,成本较高。另外,该岩层内常含有少量其他岩性的岩体,离散性大。在上述各因素影响下,较难进行重复性、验证性试验。

在地质力学模型试验中,经常使用岩土相似材料进行相关分析[21]。近些年,国内相关学者对岩石相似材料进行了深入研究[22-26]。其中,文献[23]指出,岩石相似材料的单轴抗压强度具有相当高的力学代表性。文献[24-25]通过对影响相似材料性质的相关因素进行分析,发现相似材料的强度参数和弹性模量等变形参数主要受到材料组分中胶结剂含量的影响,其黏聚力则受到骨料性质的影响。文献[26]通过对砂岩相似材料进行正交试验,也发现相似材料的抗压强度可以通过调节骨料含量实现。根据上述成果,本研究考虑使用室内浇筑的水泥砂浆试样进行试验,通过调节水泥、石英砂、水的比例使相关的强度变形参数达到要求。由于本研究主要分析试样在真三轴条件下的强度及变形特性,故分别对各配比情况下的水泥砂浆试样进行巴西劈裂试验、单轴及常规三轴压缩试验,将计算得到的相关物理力学参数与表1进行对比,确定出适用于本研究条件的最佳配比,以进行进一步的研究。各配比情况下试样的应力—应变曲线和物理力学参数如图1和表2所示。

表1 粉砂岩的物理力学参数Table 1 Physical and mechanical parameters of siltstone

图1 配比试验结果Fig.1 Results of ratio test

将表2所列出的配比试验结果与表1所列出的粉砂岩物理力学参数进行对比,最终选用水泥∶石英砂∶水配比为1∶0.8∶0.45浇筑试验所用的试样。煤样和浇筑试样尺寸均为50 mm×50 mm×100 mm(长×宽×高),对试样表面精细打磨,使其不平行度和不垂直度均小于0.02 mm,以减小试验误差。

表2 配比试验参数Table 2 Parameters of ratio test

1.2 试验装置

本研究真三轴试验采用中国矿业大学深部岩土力学与地下工程国家重点实验室自行研制的岩石真三轴电液伺服加载试验系统,如图2所示。该试验系统主要由三向伺服控制加载系统、真三轴压力室、自动采集系统等部分组成。在3个方向均具有独立伺服控制系统,可以实现3个方向同步或异步位移或载荷控制,能够有效模拟实际状态下煤与岩体的三向应力状态[27]。

图2 真三轴试验系统及加载装置Fig.2 True triaxial compression test system and loading device

1.3 试验方案

煤样和岩样的加载方案如图3所示。试验过程中先施加三向应力(3个方向加载大小分别为σ1、σ2、σ3)直至静水状态,再继续施加σ2,直到σ2达到预设值,最后以一定速率均匀增加σ1直至试样产生破坏。分别对煤样和水泥砂浆试样进行两组试验,第1组恒定σ3=4 MPa,σ2=4、6、8、10、12 MPa;第 2组恒定σ3=6 MPa,σ2=6、8、10、12、14 MPa,即共计20次试验。其中,试样的应变从σ2和σ3均达到预设值时开始计算。

图3 真三轴试验加载方案Fig.3 Loading program of true triaxial compression test

2 试验结果分析

2.1 强度特征分析

煤岩单体的强度直接决定了巷道的开挖及支护方式。通过对煤样和水泥砂浆试样进行加载试验,得到了试样在真三轴条件下的峰值强度特征曲线,如图4所示。

图4 煤岩单体的峰值强度特征曲线Fig.4 Strength characteristics curves of coal-rock single body

由图4可知:煤样与水泥砂浆试样的峰值强度相差不大,总体上看,水泥砂浆试样的峰值强度略高于煤样;煤样和水泥砂浆试样的峰值强度都是随着σ2的增加呈先增加后降低的趋势,即表现出中间主应力效应[28]。根据变形分析结果同样可以发现,煤样和水泥砂浆试样在ε1方向的峰值应变与峰值应力的变化趋势相似,也随着中间主应力的增大,峰值应变先增大,然后逐渐减小。导致这种现象的主要原因是,σ2初始的增长会使试样内部沿该方向屈服的微元体需要更高的轴向应力,也可能会使一部分微元体改变滑移方向,从而在一定程度上抑制微裂隙发育,延缓试样的破坏,宏观上表现为该试样的强度得到提升。而当σ2较大时,试样材料也会在σ2-σ3方向发生屈服,此时裂隙发育贯通,导致试样的破坏加剧,所以继续增加σ2将会导致试样强度降低[29]。

本试验中,试样的峰值强度、峰值应变随σ2的增大而呈现出的这种先增大后减小的趋势,表明中间主应力对围岩的受载破坏起到一定的保护作用,而当中间主应力到达某一临界值后,继续加大会导致峰值强度和峰值应变开始出现减小趋势,这说明中间主应力的提高对围岩的保护并非是恒定的,中间主应力过大也会使围岩破坏加剧[29]。

由图4进一步分析可知:①σ3=6 MPa对应的峰值应力普遍高于σ3=4 MPa对应的峰值应力,对煤样来说,这种趋势在最大峰值应力处附近最为明显,而对于水泥砂浆试样来说,这种趋势在曲线下降段最为明显,且σ3的增加会延后最大峰值应力点的出现。②由于σ3的变化,峰值强度随着σ2的增加呈现出的上升速率和下降速率都受到不同程度的影响。从以上变化规律中可以看出,最小主应力σ3大小会一定程度地影响中间主应力效应[30]。

强度准则能够为结构计算和设计提供理论支持,但传统的Hoke-Brown以及Mohr-Coulomb准则未考虑σ2的影响,无法有效反映实际工程中煤岩体的受力状况,不适用于本研究情形。国外的一些研究成果[31-33]表明,基于 Mises准则的 Mogi-Coulomb准则[34]在多数情况下与岩石加载试验结果吻合较好。其中,Mogi-Coulomb的线性形式与真三轴试验结果的拟合度较高,其表达式可用八面体剪应力τoct与有效中间主应力σm,2进行表示:

式中,a、b为系数,可通过拟合获得;τoct为八面体剪应力,MPa;σm,2为有效中间主应力,MPa。

τoct和 σm,2可根据峰值点的 σ1、σ2、σ3值按式(2)和式(3)进行计算:

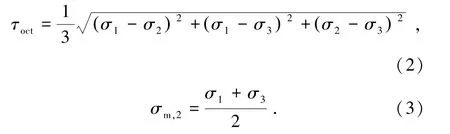
将试验数据进行Mogi-Coulomb强度准则拟合,结果如图5、图6所示。由图5和图6可知:Mogi-Coulomb强度准则能够很好地反映岩石的强度特征,拟合度为0.866～0.970。

图5 煤样的Mogi-Coulomb强度准则拟合结果Fig.5 Fitting results of Mogi-Coulomb criterion for coal samples

图6 水泥砂浆试样的Mogi-Coulomb强度准则拟合结果Fig.6 Fitting results of Mogi-Coulomb criterion for cement mortar samples

2.2 变形特征分析

在煤矿开采过程中,煤岩体的变形特征将很大程度影响巷道开挖及支护方案选择,为了分析中间主应力对煤样及水泥砂浆试样变形的影响,分别绘制了相应的应力—应变关系曲线图。其中,煤样和水泥砂浆试样的主应力差值(σ1-σ3)与相应应变(ε1、ε3)的关系曲线如图7和图8所示。

图7 真三轴状态下煤样应力—应变曲线Fig.7 Stress-strain curves of coal samples under true triaxial compression condition

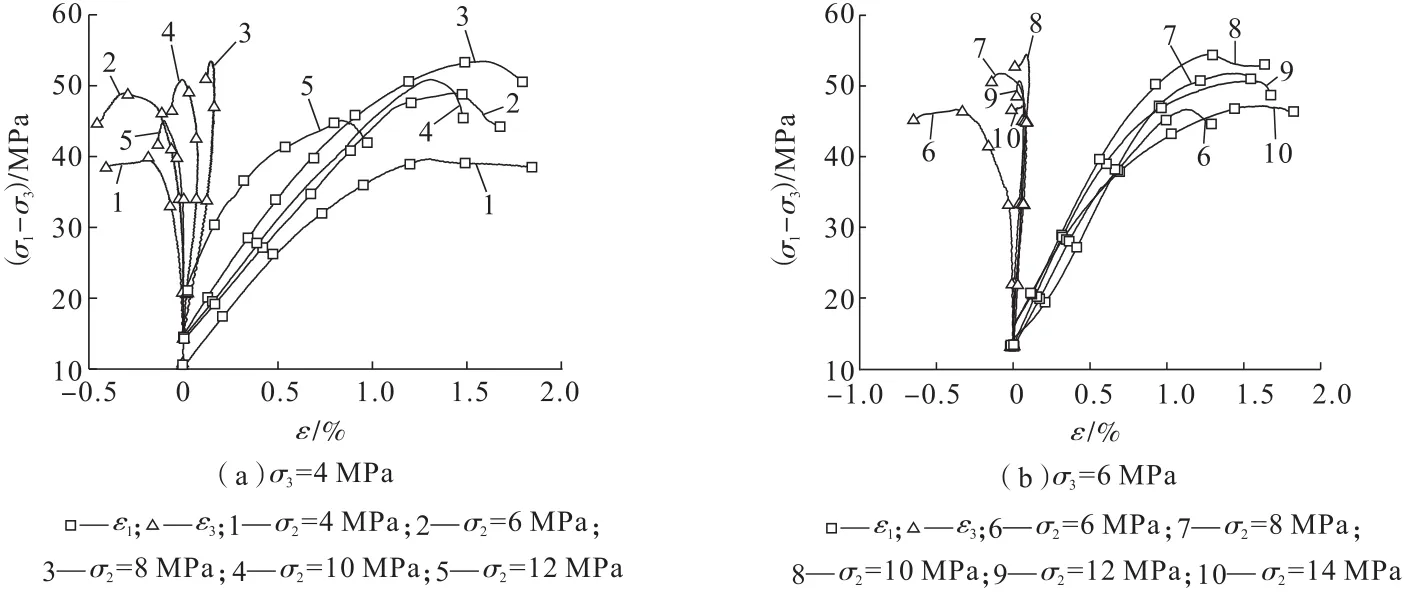
图8 水泥砂浆试样应力—应变曲线Fig.8 Stress-strain curves of cement mortar samples under true triaxial compression condition

由图7和图8可知:煤样和水泥砂浆试样在ε1方向的峰值应变也表现出随着中间主应力的增大先增大后减小的趋势。各曲线峰后段斜率大小都随着σ2的增加而增大,即试样在达到峰值强度后跌落速度加快,这表明在σ3保持不变、σ1不断加载的过程中,中间主应力σ2增加会导致试样经历延性—脆性的转化,与已有的一些研究结果[29,35]相符。一般认为,岩石破坏是由作用在岩石上的应力差σ1-σ3引起的[35-36],但已有研究认为岩石的破坏不一定发生在σ1增长的过程中,也可以发生在σ2增加和减小的过程中[36],本次试验结果即验证了这一点,即:岩石的破坏是σ1-σ3和σ2共同作用的结果。

进一步分析图7和图8可知:煤样在ε3方向的变形以膨胀为主,随着加载的进行,其变形量不断增大,且由于σ3=4 MPa时侧向约束较弱,其ε3方向的变形量明显大于σ3=6 MPa时的变形量;水泥砂浆试样在ε3方向的变形以压缩为主,侧向压力较小时,随着加载的进行,ε3会经历由压缩向膨胀的转化过程。

受初始力控制阶段的影响,真三轴条件下的煤样和水泥砂浆试样的应力—应变曲线几乎没有微裂纹压密阶段,并快速进入弹性变形阶段[37],且不同σ2条件下弹性阶段的ε1和ε3曲线都呈现极好的线性性质。弹性模量是评估弹性变形阶段的重要因素之一,应力—应变曲线的斜率直接反映了材料的弹性模量。分别计算了各个曲线σ1方向的弹性模量如图9所示。

图9 煤岩单体在真三轴条件下的弹性模量特征曲线Fig.9 Elastic modulus characteristic curves of coal-rock single body under true triaxial condition

由图9可知:①水泥砂浆试样弹性模量明显大于现场的煤样;②煤样和水泥砂浆试样的弹性模量都随着侧向压力(σ2、σ3)的增大而增大,这是因为侧向压力对试样内部微裂隙起到了挤压密实作用,提高了岩样的密实度,宏观表现为弹性模量的增大[38],但这种趋势会由于密实度的不断提高而受到限制;③而当σ3较小且保持不变时,σ2的增大对岩石的弹性模量也有一定的提高作用,但这种作用受到σ3的影响且会逐渐降低,在较高的中间主应力下,弹性模量增长速率会逐渐降低并最终趋于稳定。

2.3 破坏模式分析

尽管水泥砂浆试样在强度和变形方面能够和顶板的粉砂岩表现出很高的相似性,但由于试样的破坏模式极大地取决于其材料本身的微观结构,人工浇筑的材料很难和天然形成的粉砂岩表现出相似的破坏特征。且由于巷顶的煤体直接和临空面联系,煤样的破坏模式分析更具有实际参考意义,故本部分的破坏模式分析只针对煤样展开。一般来说,破坏模式可以通过对试样表面的裂纹进行分析得到,从而获知试样内部的受力特点。宏观上看,两组煤样的表面裂纹大致相同,故选取σ3=4 MPa时的5个煤样进行分析,如图10所示。

图10 真三轴状态下的破坏煤样(σ3=4 MPa)Fig.10 Failure coal samples under true triaxial compression condition (σ3=4 MPa)

由图10可知:

(1)裂纹主要分布在σ2作用面,而极少出现在σ3作用面,这主要是因为σ2限制了煤样在该方向上的位移[37]。

(2)当σ2与 σ3相差较小(σ2=4～6 MPa)时,裂纹主要沿着与轴线成30°～45°的方向扩展,两条裂纹近似呈“V”形,即共轭剪切破坏;当σ2进一步增大时,裂纹沿着大约与轴线呈45°的方向扩展,裂纹近似平行,破坏模式为斜截面剪切破坏。以上两种破坏形态都是由于裂隙面上的剪应力达到了其极限值[19]。当σ2与σ3相差较大(σ2=10～14 MPa)时,裂纹在沿与轴线成30°～45°的方向扩展的同时,也开始出现近似平行于轴向的竖直裂纹。即此时试样开始同时表现出剪切破坏和劈裂破坏的特征,这主要是在沿σ3方向的应变超过了其极限值导致的[19]。综上所述,当σ3保持不变时,煤样的破坏模式发生了从剪切破坏向拉伸破坏的转变趋势,这是因为当保持σ3不变时,σ2逐步增大,σ3方向的相对约束减弱,煤样在受到其他两个方向的压力后,在σ3方向产生的位移也会逐步增大,进而导致该方向的拉应变超过极限值,表现出拉伸破坏特征。

(3)通过对图10中的5个破坏试样表面裂纹数量进行对比,不难发现裂纹的扩散程度与σ2-σ3的大小呈正相关。由此说明,在实际巷道开挖过程中,及时对临空面进行支护,可以降低最小主应力和中间主应力的差值,进而能够控制巷道围岩的裂隙发育,最终避免巷道发生失稳破坏。