概率积分预计参数的ENN优化算法

2022-05-30张劲满阎跃观李杰卫徐瑞瑞王芷馨岳彩亚

金属矿山 2022年5期

张劲满阎跃观李杰卫徐瑞瑞王芷馨张坤岳彩亚

(1.中国矿业大学(北京)地球科学与测绘工程学院,北京 100083;2.浙江省地质勘查局浙江省地矿建设有限公司,浙江杭州 310052;3.安徽省煤田地质局,安徽合肥 230088;4.安徽理工大学空间信息与测绘工程学院,安徽淮南 232001;5.聊城大学地理与环境学院,山东聊城 252000)

地下煤炭资源开采后会导致一系列地质灾害,如下沉盆地、塌陷坑及台阶裂缝等,给矿区人民的生产生活和生态环境带来了一系列危害[1-3]。为了最大限度降低开采沉陷引起的矿区地质灾害,以便提前采取合理的防范措施,对煤炭资源采出后引起的地表移动变形进行精准预计显得尤为重要[4]。概率积分法预计模型作为我国矿山开采沉陷领域应用最为广泛且较为成熟的方法,近年来不少学者围绕其预计参数解算精度进行了深入研究[5-9]。贾新果[5]针对开采沉陷参数反演方法存在收敛过早现象采用蚁群算法求解,提高了抗干扰能力和求参精度;张劲满等[6-7]采用双参数Knothe时间函数建立了动态下沉模型,模型参数采用最小二乘拟合方法求解,工作面开采沉陷全过程预计精度较可靠;李培现等[8]采用地表空间移动矢量并结合遗传算法建立了参数反演方法,解决了初值依赖和多工作面难以精确反演的难题。近年来随着计算机技术快速发展,各种智能优化算法在概率积分参数获取中得到广泛应用[10-13]。利用智能优化算法获取概率积分预计参数具有计算机编程易实现且预测精度高的特点[14-18],其中常用的智能优化方法有BP神经网络和ENN神经网络。

BP神经网络是一种前馈型的网络,达到全局优化的时间较长且容易陷入局部最优解,ENN网络比BP神经网络多了一个记忆层,会使得整个网络具有更为丰富的动态性和更强的鲁棒性,参数预计精度也会得到较大提升。基于此,本研究将蚁群算法(ACO)与ENN神经网络相结合,提出一种基于ACOENN的概率积分预计参数计算模型,该模型有助于解决ENN神经网络初始权值与阈值选择依据不充分的难题,使得模型预测精度更高、可靠性更强。

1 ACO优化ENN神经网络

1.1 ENN神经网络

ENN神经网络是一种前馈式神经网络,网络中的延时算子具有记忆功能,使得系统具有较强的适应时变特性的能力,进而具备反映动态过程系统的能力。ENN神经网络由输入层、隐含层和输出层组成,其中隐含层中加入了一个承接层,增强了ENN神经网络对历史信息的敏感性,并提高了神经网络应对突变的能力。ENN神经网络结构如图1所示。

图1 ENN神经网络结构Fig.1 ENN neural network structure

首先构建ENN神经网格并对其进行训练,使其具有历史信息记忆和动态反馈机制,提高ENN神经网络处理动态信息的能力。ENN神经网络的数学表达式为

式中,w1为承接层至中间层的连接权值;w2为输入层至中间层的连接权值;w3为中间层至输出层的连接权值;u(t-1)为输入量;b1为输入层阈值;b2为隐含层阈值;g(·)为输出神经元的传递函数,一般采用purelin函数;f(·)为中间层神经元的传递函数,一般采用tansig函数。

ENN神经网络采用误差反传法使得输出层的实际值与期望值之间的误差值达到设定的最优值,误差公式为

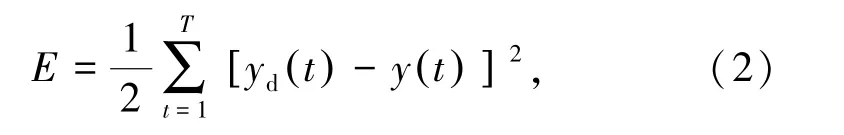
式中,yd(t)为第t个节点的实际输出值;y( t)为第t个节点的期望输出值。

在ENN神经网络学习过程中需要不断地优化权值并获取最优阈值。一般采用梯度下降算法实现权值寻优,其权值更新公式为

式中,E为误差函数;η为学习率;ΔW为隐含层权重修正量。

此外,ENN神经网络阈值寻优一般采用激励函数实现,其阈值更新公式为

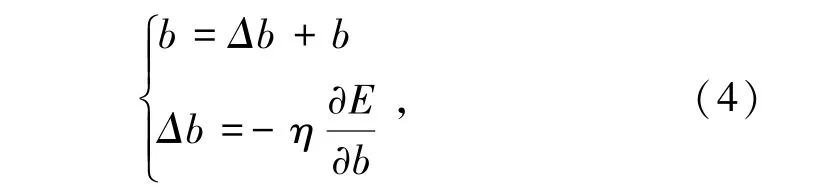
式中,Δb为隐含层阈值修正量;b为阈值。

1.2 ACO算法

ACO是一种模拟生物群体觅食的正反馈、启发式随机搜索算法,具有鲁棒性好、全局搜索能力强等优点,对非线性问题求解具有较好的适应性。在蚁群算法正反馈作用下,蚂蚁选择路径的概率表达式为

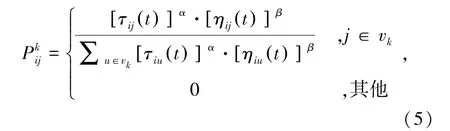
信息素更新在蚂蚁寻路过程中起着至关重要的作用,信息素会挥发和叠加,其更新的数学表达式为

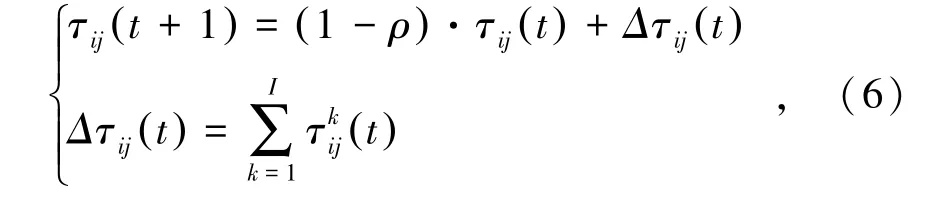
式中,τij(t+1)为t+1时刻位置i至位置j的信息素浓度;Δτij(t)为蚂蚁种群I在时间段(t,t+1)位置i至位置j的信息素浓度增加量;ρ为信息素的挥发系数;I为蚂蚁种群数;(t)为蚂蚁k在t时刻位置i至位置j的信息素浓度。

1.3 ACO-ENN模型构建

本研究采用ACO算法优化ENN神经网络,构建了ACO-ENN优化模型用于解算概率积分预计参数,流程见图2。具体步骤为:①确定输入层、输出层及隐含层的节点个数,确定ENN神经网络结构,初始化ENN神经网络并对网络参数进行配置;②初始化ACO参数并构造信息素矩阵,利用ACO算法对ENN神经网络的权值和阈值进行优化,获取ENN神经网络的初始权值和阈值。③采用优化后的权值和阈值进行ENN神经网络学习预测。

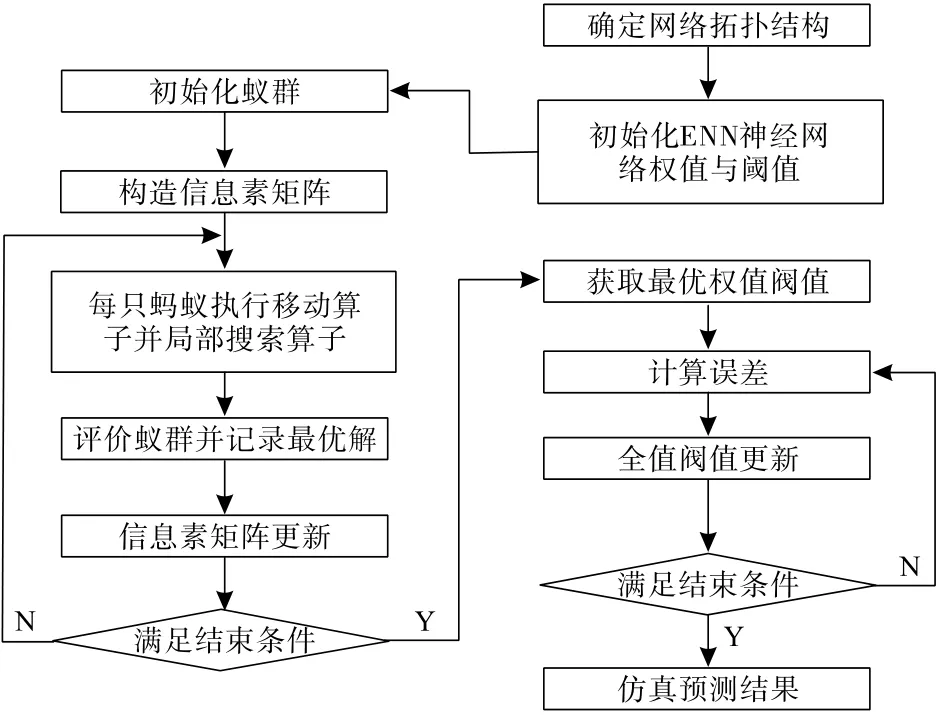
图2 ACO-ENN模型优化流程Fig.2 Optimization flow of ACO-ENN model

2 试验分析

2.1 试验数据选取

本研究选取我国典型矿区的30个地表移动观测站实测资料作为训练和测试的样本数据[13],每组样本数据由地质采矿条件和概率积分预计参数两部分组成。地质采矿条件包括覆岩坚固系数、采深、采厚、松散层厚度、煤层倾角及采动程度,概率积分预计参数包括下沉系数、水平移动系数、主要影响角正切及拐点偏移距。选取的样本数据见表1。

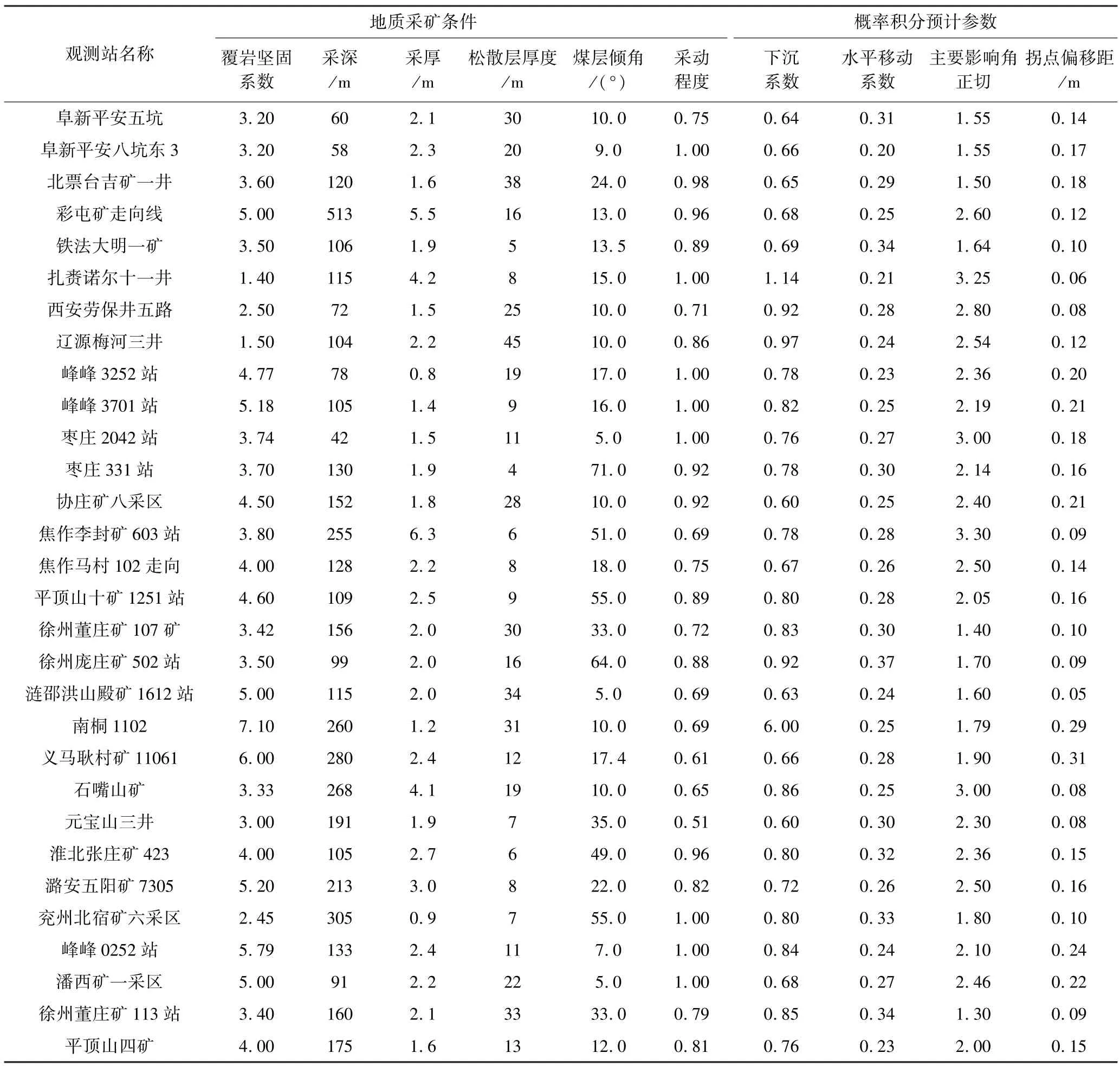
表1 实测样本数据Table 1 Measured sample data

2.2 ACO-ENN模型参数设置

为了精确获取概率积分预计参数,本研究将地质采矿条件因素作为ACO-ENN模型的输入节点,即输入层由6个神经元组成,对应6个影响因素,概率积分预计参数的各个参数分别作为ACO-ENN模型的输出节点,即输出层1个神经元,对应概率积分预计参数的各个参数。经过不断优化训练可得各个模型的隐含层最优神经元个数分别为:下沉系数网络模型神经元10个,水平移动系数网络模型神经元8个,主要影响角正切网络模型神经元11个,拐点偏移距网络模型神经元11个。初始种群数为I为30,信息素的挥发系数ρ为0.9,重要程度系数α为0.3,启发式的重要程度系数β为0.5。

2.3 数据预处理

由于现场观测环境往往十分复杂,数据采集过程中难免会有一定的误差,此外,训练样本数据和测试样本数据常存在不同程度的差异性。为降低数据采集误差和训练样本输入层数据与测试样本输入层数据的差异性,在数据训练之前需要将输入层的样本数据进行降噪处理。RW是一种基于加权最小二乘算法对离散数据进行多项式拟合的降噪方法,采用稳健的拟合处理方式以防止偏离点扭曲了平滑的数据点。本研究采用RW方法对实测数据进行降噪处理,降噪后的数据与实测数据对比如图3所示。

由图3可知:经过RW降噪处理后数据的上下波动范围明显降低,处理后的数据曲线更加平滑。对一些波动范围较大的数据点进行降噪处理有助于降低数据测量误差和选择不合适训练样本数据带来的误差影响。

图3 实测样本数据与RW降噪处理后的结果Fig.3 Measured sample data and results after RW noise reduction processing

2.4 解算结果及分析

将前25组实测样本数据作为训练样本对网络进行训练,剩余5组实测样本数据作为测试样本。采用ACO-ENN模型对RW降噪处理前后的数据进行训练并求取概率积分预计参数,实测数据和降噪处理前后ACO-ENN模型预测的概率积分参数如图4所示。由图4可知:采用RW方法预先进行了预处理后,再进行ACO-ENN预测,获取的概率积分参数预计值精度优于ACO-ENN模型预计值,反映出采用RW法对原始样本数据进行预处理有助于提高数据质量。

图4 概率积分参数预测值与实测值对比Fig.4 Comparison of the predicted and measured values of expected parameters

基于RW方法进行降噪预处理后的样本数据分别采用ACO-ENN模型和传统的ENN神经网络对下沉系数、水平移动系数、主要影响角正切和拐点偏移距进行预测,预测结果如图5所示。由图5可知:在下沉系数和水平移动系数预测过程中ACO-ENN模型的预测精度优于ENN神经网络,可靠性更强,在主要影响角正切和拐点偏移距的预测过程中ACO-ENN模型的预测误差绝对值整体小于ENN神经网络,预测精度较高。概率积分各预计参数的平均预测相对误差和均方根误差见表2。由表2可知:利用ACOENN模型解算下沉系数、水平移动系数、主要影响角正切及拐点偏移距的平均相对误差分别为2.41%、3.48%、6.11%和1.67%,ACO-ENN模型解算结果的平均相对误差和均方根误差均优于传统ENN神经网络,表明ACO-ENN模型解算精度更高、可靠性更强。