基于转角数据的梁式桥挠度响应重构方法

王宁波， 赵雨森， 贺 政， 黄天立

(中南大学 土木工程学院，长沙 410075)

桥梁结构在荷载作用下的挠度信息是反映结构状态及性能的重要参数，在现阶段土木工程基础设施逐渐老化的大背景下，开展桥梁挠度信息准确测量的技术和方法研究意义重大。

现有的桥梁挠度测量主要方法包括：位移传感器(linear variable differential transformer,LVDT)测量[1]、水准仪/全站仪测量[2]、连通管液位式[3]、GPS传感器[4]、机器视觉[5-6]、激光/雷达测试[7-9]等。整体而言，这些直接测试方法大多需要选定不动点作为相对测量参考点。利用LVDT和激光测试进行桥梁挠度变形测量时参考点离测点最近(一般将LVDT固定在桥梁正下方)，这种采用接触式测量方式可实现高精度、动态测试。但该固定参考点的搭设需要特定的外部条件，且存在较大的经济消耗，激光测试同时受天气影响较大[10]。水准仪/全站仪测量挠度时，一般选梁上较远处不动点作为参考点，大多只能进行静态测量且测试精度有限[11]。GPS和雷达操作复杂，难以满足桥梁挠度高精度测试需求，且在桥梁实际检测中应用较少[12-13]。而机器视觉法是典型的非接触式测量，借助连续拍照和图像处理技术可实现对挠度信息的动态测量，但要求其拍摄点固定不动，其测试精度还受拍摄距离、光线、角度等因素影响。目前仍只能在室内试验环境中获取高精度测试结果[14]。

结合其他更易于直接获取的结构响应数据(如：桥梁转角)来重构挠度响应，即挠度间接测试也是重要的研究思路。李勇等[15]通过对实测倾角值进行数值积分与曲线拟合得到桥梁挠度曲线，并结合简支梁、悬臂梁模型试验验证其可行性。Li等[16]使用光纤陀螺测量结构的角速度，对时间积分得到挠曲线轨迹的角度变化，再以此进行区间积分得到结构挠度曲线。这类方法简单直接，但往往需要大量测点来保证准确性，且由于存在积分过程，其结果受测试干扰影响较大。Sanli等[17]将挠度变形假设为三次多项式函数，结合实测倾角数据，并基于最小二乘法拟合出挠度曲线。Ooi等[18]将该思路用于重构墙体的变形。基于样条函数拟合的方法需要的测点数少，但三次函数并不适用于复杂的桥梁或荷载形式。侯兴民等[19]采用基函数描述桥梁挠曲线，利用QY型倾角仪实测桥梁倾角数据，以此确定基函数组合系数从而获取挠度响应曲线。该方法对倾角测点的数量有一定要求，其基函数(多项式)的次数由测点数确定，不具物理意义。杨小森等[20]利用桥梁的自振振型作为基函数，实现结构倾角与挠度转换，但实际结构振型向量难以准确获取[21-22]。

总体而言，结合转角数据进行挠度响应重构的问题尚未很好解决，既有方法多依托于大量倾角传感器，存在时间、经济方面的较大消耗。Lan等[23]提出将倾角仪搭载在小车上进行测试的思路，小车移动到不同截面位置进行倾角测试，本质上仍是多传感器测试的思路。现有响应重构方法主要聚焦在挠曲线的描述和简化，忽略了对桥梁几何参数信息、荷载位置分布信息的应用。

基于研究需求与现有不足，本文提出一种利用转角数据重构挠度响应的方法。根据桥梁几何参数和荷载位置信息建立挠度响应与转角响应之间关联，结合实测转角响应数据识别中间变量，再以此计算桥梁挠度响应信息，实现由单个转角测点数据重构桥梁挠度响应曲线。开展数值仿真和模型试验研究，验证本文方法对移动荷载和静荷载作用下桥梁挠度响应重构的正确性与可行性。

1 桥梁结构转角与挠度特征分析

对桥梁结构而言，转角与挠度均体现其荷载作用下的整体变形信息。在外荷载作用下桥梁各截面产生挠度变形的同时转角也对应发生改变。描述桥梁荷载效应时，二者具有等效性。

以简支梁桥为例，对其在车辆荷载作用下的挠度和转角响应进行对比研究。车-桥作用示意图如图1所示，假定简支梁桥跨度为Lb，桥梁实际抗弯刚度为EI(X)。其中：I(X)为桥梁截面惯性矩沿桥长方向变化的函数，为几何参数，可结合桥梁设计资料确定；E为物理参数，表示桥梁等效弹性模量。假定车辆位于x处时，对桥梁产生的荷载作用记为F(x)。

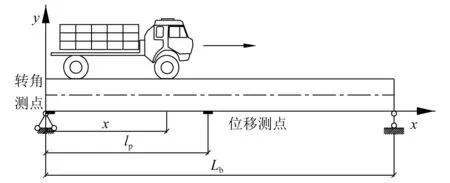
图1 车辆过桥示意图Fig.1 Schematic picture of a moving vehicle on bridge

结合单位荷载法，对桥梁左端转角及距离端部距离lp处的挠度分别进行研究。车辆荷载位于x处时，将荷载分解为F(x)与单位荷载相乘。进行荷载效应计算时可先计算单位荷载作用在x处时的效应，再结合F(x)进行叠加。单位荷载法涉及弯矩图，如图2所示。

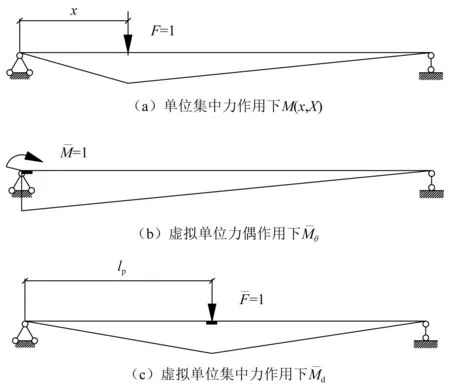
图2 测点单位力作用弯矩图Fig.2 Moment of measurement point under unit force

图2中M(x,X)表示单位力作用在x位置时，梁任意截面X处的弯矩

(1)

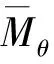
(2)

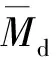
(3)

考虑车辆荷载作用位置x的变化，根据单位荷载法计算梁端转角响应Rθ(x)及桥梁挠度响应Rd(x)分别为

(4a)

(4b)

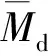
对于连续梁桥，其同一荷载作用下挠度响应和转角响应仍存在明确对应关系。相较简支梁的变形计算思路，仅M(x,X)的表达式不同。以三跨连续梁为例，由力法计算荷载作用于x处时梁的弯矩如图3所示。另一方面，计算虚拟单位力作用下弯矩时，对于超静定体系可解除多余约束，去除中间两个支座，选取简支梁为基本结构进行变形计算，其内力图形与图2(b)、图2(c)一致。

图3 连续梁在单位力作用下弯矩图Fig.3 Moment of continuous beam under unit force

基于对同一荷载作用下桥梁挠度、转角变形特征进行理论分析发现：对于梁式结构，在已知荷载信息(大小、位置等)和桥梁几何参数的情况下，桥梁挠度与转角变形存在明确对应关系。

2 结合转角数据的桥梁挠度响应重构方法

2.1 移动荷载作用下的响应重构

考虑图1中车辆荷载位置随时间前移，则在移动车辆作用下，桥梁响应与桥梁几何参数、物理参数、边界约束条件及车辆荷载信息有关。从式(4)可以看出，转角响应和挠度响应所依赖的荷载输入项和物理参数E相同，仅内力项(与几何参数相关)存在差异。将几何参数信息视为已知时，则由转角响应可重构挠度响应。

由于实际响应一般通过一定频率的采样测试获取，为离散矢量形式。将式(4)写成矩阵/矢量计算式为

(5a)

(5b)

(6)

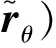
(7)

(8)

Λ中元素综合体现结构实际弹性模量以及荷载移动过程中接触力绕静态轴重的波动变化。对于不存在荷载动态变化的情况，如：准静态荷载，接触力与静态轴重之比值为1，此时αi的理论取值均为1/E。

将上式中与几何参数和车辆荷载信息相关的已知向量记为φ,ψ，即

φ=Ftn×xnMxn×xnξ

(9a)

ψ=Ftn×xnMxn×xnη

(9b)

则Λ中各元素可识别如下

(10)

(11)

2.2 静载作用下响应重构

对于静态荷载作用下的挠度响应重构，不考虑荷载位置改变，且不存在荷载动态变化。此时转角、挠度响应均为单个值。实际转角响应与几何参数满足

φ=fMxn×xnξ

(12a)

ψ=fMxn×xnη

(12b)

其中,

(13)

构建实际挠度响应

(14)

综上推导，本文提出的梁式桥挠度响应重构方法主要适用于简支梁及连续梁等梁式结构。获取桥梁几何参数和车辆车轴信息的基础上，结合合适截面转角响应即可准确重构邻近梁段截面的挠度响应。响应重构具体流程如图4所示。

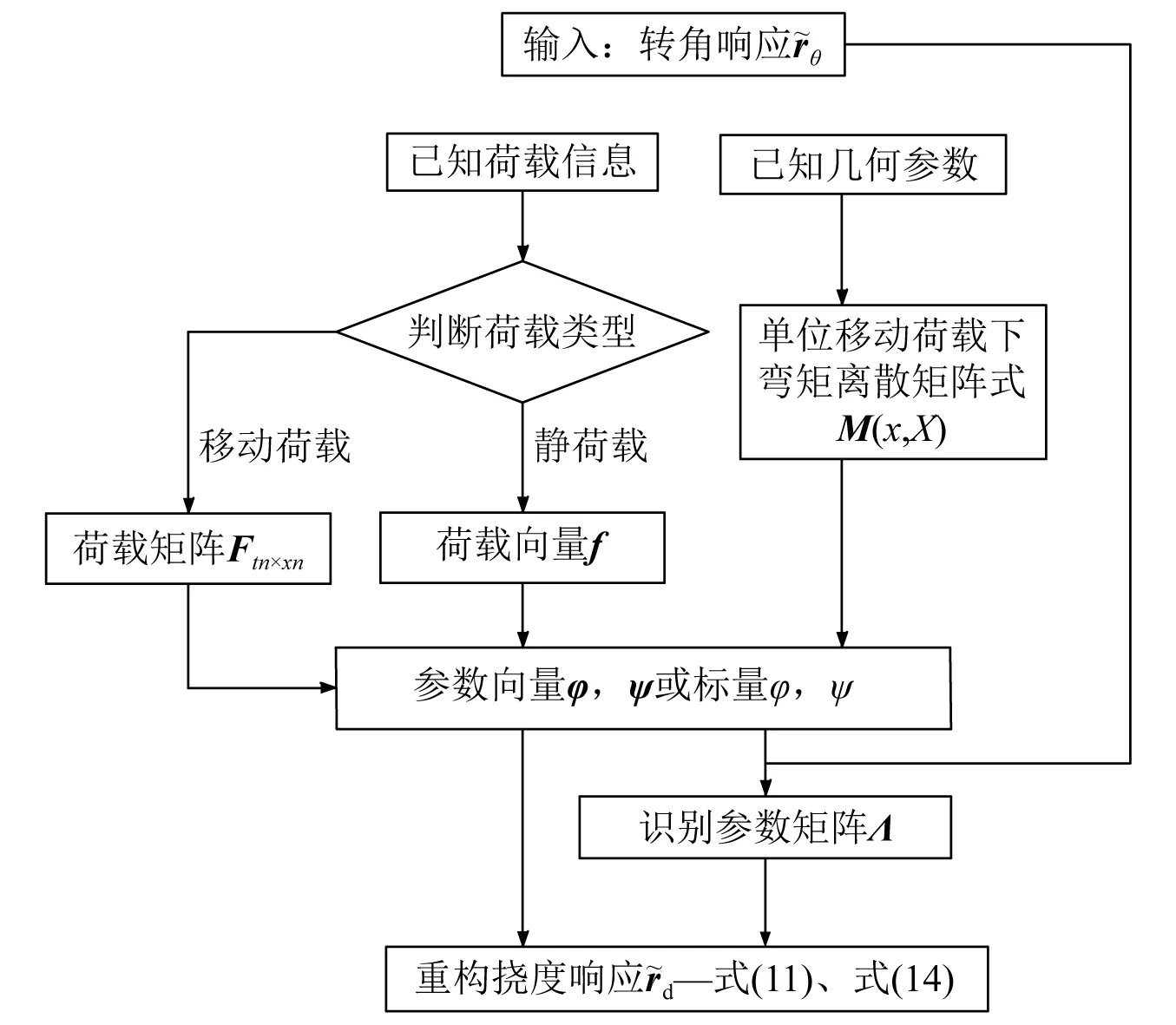
图4 挠度响应重构流程图Fig.4 Flow chart of restructuring deflection response

3 基于转角进行挠度响应重构数值仿真

结合车辆过桥数值仿真计算，开展基于转角数据的桥梁挠度响应重构，并与仿真计算挠度响应进行对比，以验证本文挠度重构方法的正确性。

3.1 建模与响应计算

以三轴车辆行驶通过连续梁桥为例，进行桥梁转角及挠度数值计算，再结合计算结果开展响应重构和结果比较。车、桥模型如图5所示，桥梁为三等跨连续梁，每跨30 m，全长Lb=90 m，抗弯刚度EI=2.38×1010N·m2，r(x)为描述路面不平度的参量；车辆具体参数源于文献[24]。

采用多刚体系统建立车辆模型、有限单元法建立桥梁二维模型，通过位移和力的协调实现二者接触。考虑桥梁结构在荷载作用下处于弹性范围内，基于结构动力学理论建立车-桥振动方程为

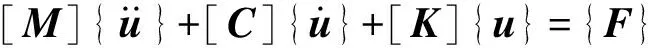
(15)

式中:[M],[C]和[K]分别为梁的质量矩阵、阻尼矩阵和刚度矩阵;{F}为荷载矢量;{u}为系统位移。

桥面平顺性等级参考国际规范ISO 8608规定，结合wilson-θ隐式积分法迭代求解系统动力响应。按频率100 Hz进行数据输出，记录车辆上桥直至完全出桥过程模拟计算的响应数据，并对计算结果附加一定比例高斯白噪声模拟实际测试噪声。

图5 车-桥耦合计算模型图(m)Fig.5 Vehicle-bridge calculation model(m)

在梁端及支点所在截面位置设置4个转角测点R1～R4，在各梁段跨中位置设置挠度测点D1～D3，如图6所示。数值仿真计算工况包括：①考虑车辆以准静态速度移动过桥，不计测试噪声；②车辆以速度v=10 m/s过桥、考虑桥面不平度等级A级和噪声5%，该工况下测点动力响应分别如图7(a)和图7(b)所示。

图6 测点布置图Fig.6 Arrangement of measurement points

图7 桥梁响应曲线Fig.7 Bridge response curve

3.2 响应重构结果比较

基于3.1节仿真计算工况(1)中准静态转角响应按本文方法重构挠度响应曲线，并将重构结果与仿真计算结果进行比较，如图8所示。

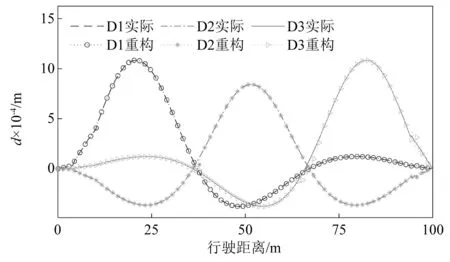
图8 准静态挠度响应及重构曲线比较Fig.8 Comparison of quasi-static deflection response and restructuring curves

可以看出，在车速较低且不考虑振动以及测试噪声的情况下，各个测点重构的挠度响应与数值计算结果均呈现高度的一致性。表明本文基于转角信息进行挠度响应重构方法的可行性。

进一步地，分析动态荷载作用下响应重构特征，结合R1、R2转角动力响应对挠度测点D1、D2、D3进行响应重构，并与其数值计算结果对比如图9所示。

图9 动态挠度响应及重构曲线比较Fig.9 Comparison of dynamic deflection response and restructuring curves

图9(a)可以看出，基于R1转角信息重构的D1挠度响应与数值计算结果存在较好一致性，二者趋势及响应波动均基本重合。重构的D2、D3挠度响应则与实际计算的响应曲线存在一定误差，尤其对于D3的重构响应尽管与实际响应的趋势一致，但局部波动误差明显。主要原因在于R1(端部)和D3(第3跨跨中)测点幅值变化不一致，当R1幅值较大时，D3幅值反而较小，重构时将波动项放大造成失真。图9(b)中，由R2转角信息重构的挠度响应中，D1和D2均与实际值保持较好一致性。另一方面相较图9(a)而言，由R2重构的D3响应曲线较R1重构的D3曲线与实际结果偏差明显下降。进一步分析，基于不同位置转角数据进行D1、D2响应重构，如图10所示。

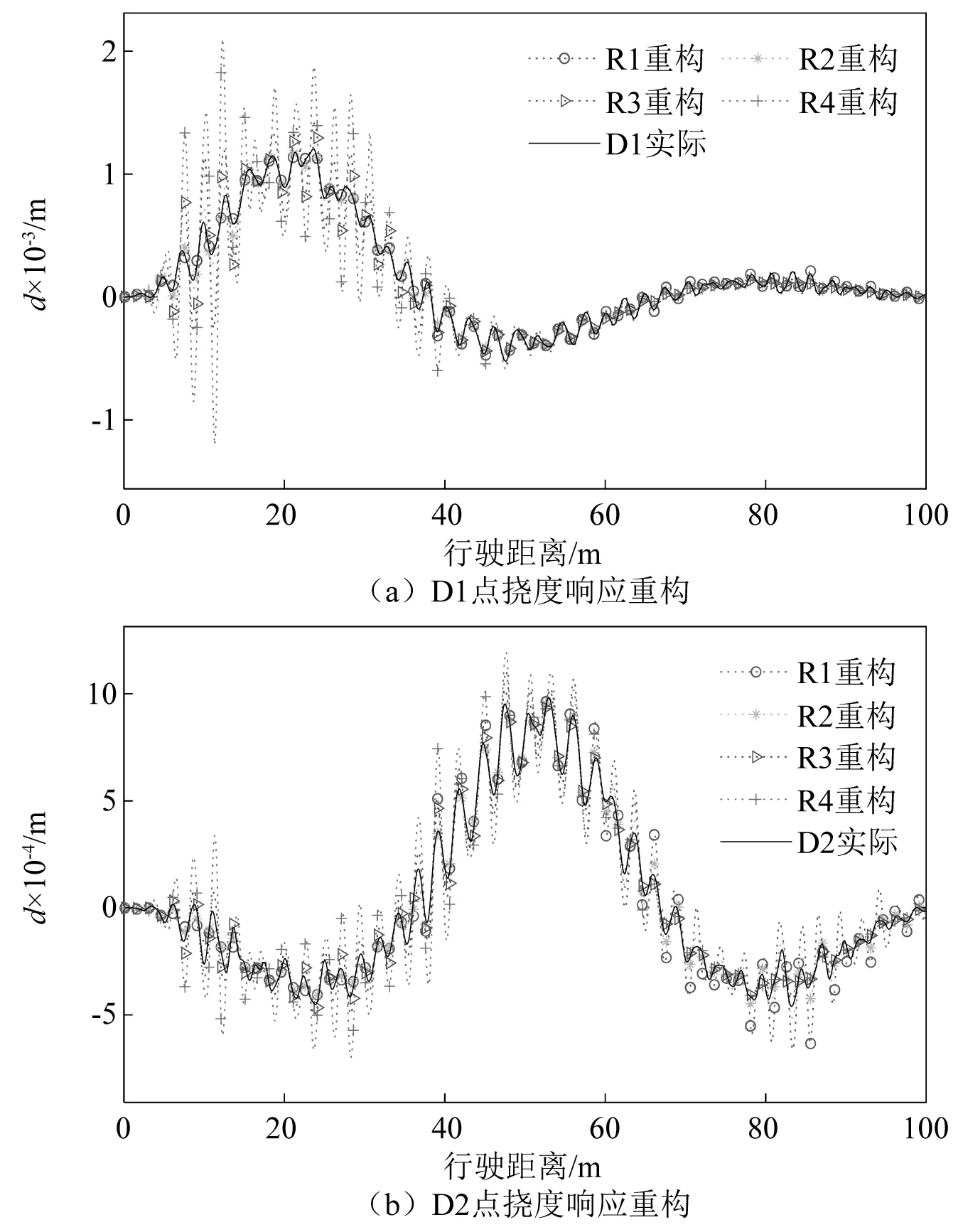
图10 结合不同位置转角数据的测点挠度重构结果Fig.10 Deflection restructuring of measuring points with different rotation angles

图10可以看出，针对D1响应的重构，基于相邻两端测点R1、R2的重构响应具有较高精确度，而由较远处转角测点R3、R4重构的响应与实际偏差较大。同样针对D2的响应重构，由R2、R3重构结果较R1、R4与实际更接近。经分析可知，当转角测点距离信号重构点位置较远时，二者存在响应幅值变化不同步的情况，响应中的振动信息难以准确重构，故可通过选取与测点相邻的支座转角信息以提高重构精度。

4 模型试验验证

4.1 试验概况

针对简支梁模型，分别测试其在静态荷载及移动荷载作用下端部转角和梁段挠度的响应，进一步验证本文结合转角进行挠度响应重构方法的正确性和可行性。

为实现车辆模型产生移动荷载，本模型试验设置辅助梁和试验梁，辅助梁上设置轨道用于限制车辆移动轨迹，如图11、图12所示。

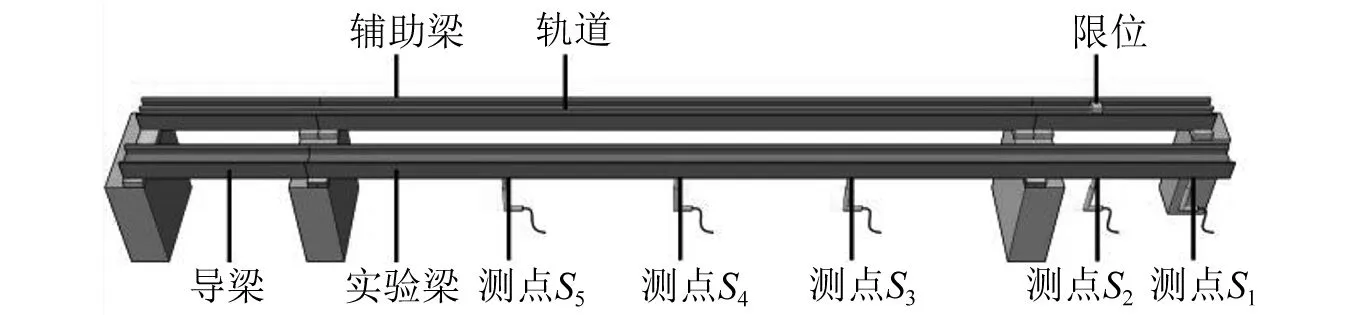
图11 试验模型布置图Fig.11 Experimental model arrangement

图12 现场试验布置图Fig.12 Field test arrangement

试验梁采用100 mm×68 mm×4.5 mm工字型钢梁，两支座间距4.25 m，且在其中一侧设置1 m长外伸段，通过测试外伸端刚体位移来确定梁的端部转角。分别在试验梁悬臂段距离支座380 mm(S1)及760 mm(S2)处设置两个位移传感器，通过两者差值检测并换算端部转角。在1/4L，1/2L及3/4L处分别设置三个挠度测点S3，S4，S5，分别布设位移传感器(传感器型号均为HBM WA-50 mm)。

试验采用一种箱式模型车，如图13所示。车体底部两个“V”型车轮与辅助梁上的轨道贴合，以保持小车沿轨道运行；另一个车轮直接作用在试验梁上，形成移动荷载，通过改变车辆负荷调整其对梁体的作用力大小。

图13 “V”型车轮布置图Fig.13 V-wheel distribution

试验加载形式涉及静态荷载和移动荷载。对于静载试验，将空车放置于加载点，以此作为测试起点，向小车中分级加入砝码。通过在车内事先放置橡胶垫片，以减小加、卸载瞬间产生的振动与冲击。待小车布置到位后对传感器数据清零开始检测，依次向小车内放入砝码，稳定后再依次卸载至零，记录全过程数据。对于移动荷载试验，首先将砝码放入小车形成一定荷载量并停置于导梁上，由牵引绳牵引小车匀速通过试验梁，并止于梁端限位处。试验采用HBM数据采集系统(MGCPlus)测试并记录传感器数据，静载试验测试频率为5 Hz，移动荷载试验测试频率为50 Hz。根据试验类型和荷载大小不同设置4组试验工况，如表1所示。

表1 试验工况Tab.1 Experimental cases

4.2 试验数据及分析

对试验所获得5个测点的位移数据进行分析，以悬臂段两个测点(S1，S2)的位移数据计算端部转角。考虑到悬臂段在试验过程中受力为零，刚体转动角度即为端部转角

Rθ=(yS2-yS1)/Δl

(16)

式中：yS1,yS2分别为S1,S2测点的位移;Δl为两测点间距离，此处为380 mm。

对于静载试验，分两级加、卸载，待响应稳定后维持约30 s，以5 Hz频率测试记录加、卸载全过程梁体挠度时程曲线。以工况1为例，试验梁1/4L，1/2L测点处的挠度实测值及基于转角数据重构值的时程曲线，如图14所示。可以看出在分级加载作用下，由端部转角数据重构的1/4L，1/2L处挠度响应与实测挠度均具有较高的一致性。

图14 静载试验下实测挠度与重构曲线Fig.14 Measured deflection and restructuring curves under static load

对于移动荷载试验，以50 Hz频率记录小车匀速过桥过程中梁体对应测点挠度随时间的变化。根据车辆上桥与出桥时间差及试验跨长计算其速度值，构建空间位置信息与时间信息的关系，基于此重构挠度响应的时程曲线。以工况3为例，由S1，S2测量的梁端转角响应以及测点S3，S4，S5处挠度响应曲线，如图15所示。可以看出，其端部转角与各个测点挠度有相似的变化趋势与波动形态。根据本文方法重构1/4L，1/2L测点处的挠度与其实测响应比较，如图16所示。可以看出，重构的动态挠度响应曲线与实测响应曲线基本重合。

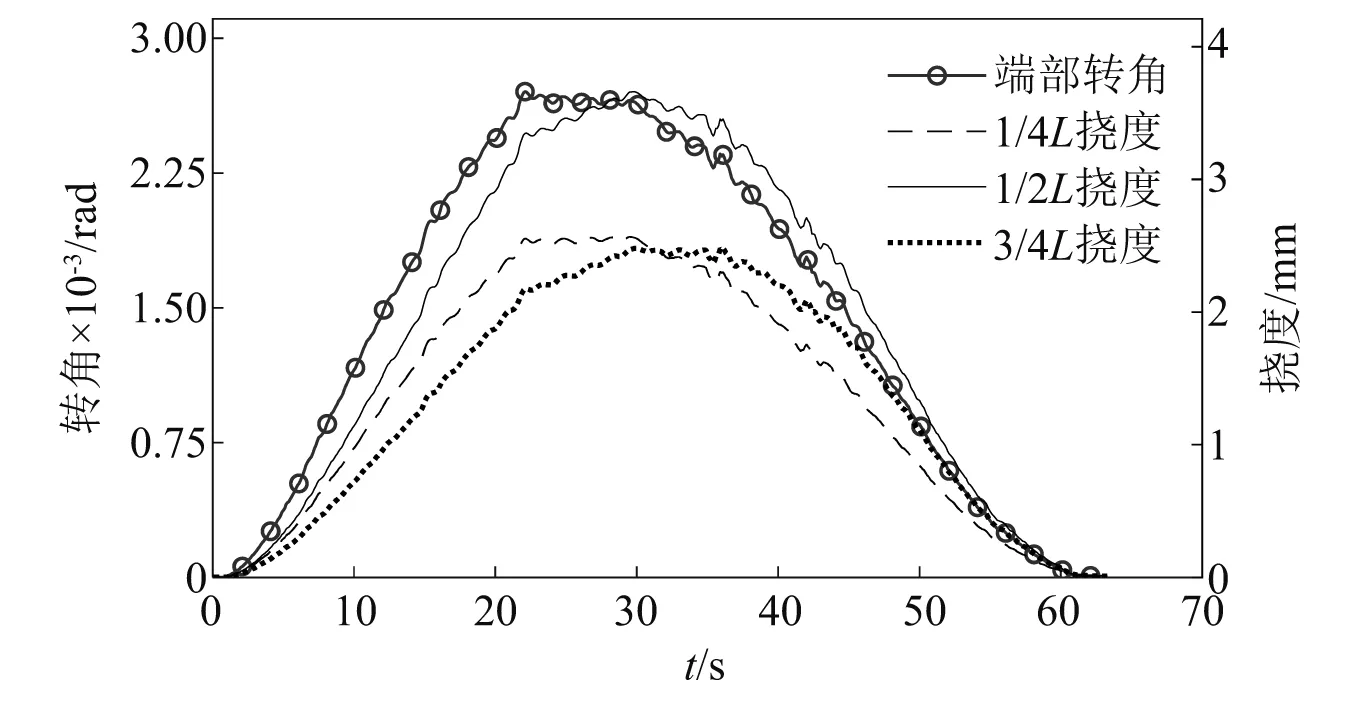
图15 移动荷载下的端部转角和实测挠度Fig.15 End angle and measured deflection under moving load

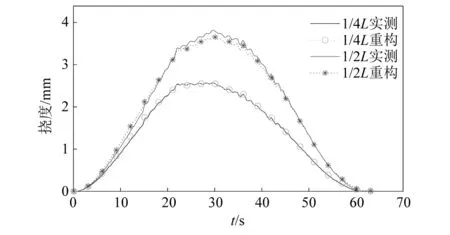
图16 移动荷载下的实测挠度和重构曲线Fig.16 Measured deflection and restructuring curves under moving load

针对表1四种工况，就其重构响应和实测响应最大值进行比较分析，列出最大值误差如表2所示。四种工况最大值偏差不超过5.4%，试验结果进一步验证了本文挠度响应重构方法的准确性与可行性。

表2 误差分析Tab.2 Error analysis %

5 结 论

本文针对桥梁挠度响应重构问题，基于充分的特征及机理分析，提出了一种基于梁端转角数据的梁式桥挠度响应重构方法，开展数值仿真和模型试验研究，得到结论如下：

(1) 梁端转角信息较挠度更易于测试获取，在桥梁荷载信息以及边界条件确定的情况下，与各位置的挠度均有严格对应关系，是用于重构挠度信息的理想参数。

(2) 数值仿真与模型试验研究表明，基于转角数据的梁式桥挠度响应重构方法具有较高的精度与可行性。

(3) 多跨桥梁动力响应重构时，相距较远的测点存在振动幅值上的差异，重构响应时易于将此放大而产生误差，选取与挠度测点临近的支座转角数据，更利于准确重构测点动力响应。

(4) 本文转角到挠度的转换方法仅需要荷载信息、桥梁几何参数和梁端实测转角响应即可重构挠度响应，无需布置较多转角测点，有较好的实用性。