2021年北京卷压轴题的研究

安徽省芜湖市第一中学 刘海涛 241000

《中国高考评价体系》指出：高考要求学生能够触类旁通、举一反三，甚至融会贯通，既包括同一层面横向的交互融合，也包括不同层面之间纵向的融会贯通.高考客观上对高中教学起到重要的引导作用，因此在教学过程中，对于一些高考真题，如果我们能够从不同角度思考，寻求不同的解法，并将其推广到一般化情形，定能加深对问题的本质认识，从而拓宽解题视野，发散解题思维，提升学习兴趣，提高解题能力[2].本文是笔者对2021年北京高考数学压轴题的研究，现与读者分享交流.

1 试题呈现与分析

（2021 年北京卷·第21 题）定义Rp数列{an} ：对∀p∈R 满足：①a1+p≥0，a2+p=0；②∀n∈N*,a4n-1＜a4n；③∀m,n∈N*，am+n∈{am+an+p,am+an+p+1} （.1）对于前4 项分别是2 ，-2 ，0 ，1 的数列，可以是R2数列吗？说明理由；（2）若{an} 是R0数列，求a5的值；（3）是否存在p∈R，使得存在Rp数列{an}（其前n项和是Sn），对任意n∈N*，满足Sn≥S10？若存在，求出所有这样的p；若不存在，说明理由.

分析：该题形式上以集合为载体考查数列，主要考查了用递推方法、分类讨论思想解决问题的能力，需要用到猜想、归纳、证明结论，并利用新的结论解决问题，体现了逻辑推理、数学运算等数学核心素养.第（1）、（2）两问属于常规问题，本文不再赘述，重点论述第（3）问，向读者介绍笔者的研究.

2 解法探究

解析：（1）不是R2数列（理由略）；（2）a5=1（过程略）；

（3）思路1：由Sn≥S10得a10≤0 ≤a11，于是想到先“必要性探路”，再“充分性验证”的方法，首先根据条件中的递推关系得到a10和a11，结合a10≤0 ≤a11，得到p的值，再对该值进行充分性证明即可.

方法1：假设存在满足条件的Rp数列{an} ，其前n项和Sn的最小值为S10，则a10≤0 ≤a11.

由③知-p=a2∈{ }2a1+p,2a1+p+1 ，而2a1+p+1 ≥-p+1 ＞-p，则-p=2a1+p，即a1+p=0 .由③知a3∈{a1+a2+p,a1+a2+p+1} ={-p,1-p} ，a4∈{2a2+p,2a2+p+1} ={-p,1-p} ，又由②知a3＜a4，则a3=-p，a4=1-p. 由③知a5∈{a1+a4+p,a1+a4+p+1}∩{a2+a3+p,a2+a3+p+1}={1 -p,2-p} ∩{-p,1-p} ={1 -p} ，则a5=1-p. 由③知a6∈{1 -p,2-p} ∩{-p,1-p} ={1 -p} ，则a6=1-p.由③知a7∈{1 -p,2-p} ，a8∈{a2+a6+p,a2+a6+p+1} ={1 -p,2-p} ，又由②知a7＜a8，则a7=1-p，a8=2-p. 由③知a9∈{2 -p,3-p} ∩{1 -p,2-p} ={2 -p} ，则a9=2-p.由③知a10∈{2 -p,3-p} ∩{1-p,2-p} ={2 -p} ，则a10=2-p.由③知a11∈{2-p,3-p} ，a12∈{a2+a10+p,a2+a10+p+1} ={2-p,3-p} ，又 由②知a11＜a12，则a11=2-p，a12=3-p. 于 是 有2-p≤0 ≤2-p，解 得p=2，为Sn≥S10的一个必要条件.

下面验证条件p=2 的充分性.当p=2时，由前述分析得a1=a2=a3=-2，a4=a5=a6=a7=-1，a8=a9=a10=a11=0 ，a12=1，则S10=min{S1,S2,…,S11,S12} ，欲证Sn≥S10，需证当n≥12 时an＞0.下用数学归纳法证明.当n=12 时，a12=1 ＞0，命题成立；假设n=k（k≥12，k∈N*）时，命题成立，即ak＞0.当n=k+1 时，k-7 ≥5，由ak+1∈{a8+ak-7+2,a8+ak-7+3} ，则ak+1≥a8+ak-7+2=ak-7+2 ＞-1+2=1 ＞0；综上，得当n≥12 时an＞0.

评注：“先充分后必要”法是探究性问题的通性通法之一，

思路2：由题设条件分析数列{ }an的递推关系，归纳猜想出通项公式，用数学归纳法证明猜想，最后用通项公式解题.

方法2：由③知a2∈{2a1+p,2a1+p+1} ，而2a1+p+1 ＞-p，则-p=2a1+p，即a1=-p.由③知an+1∈{a1+an+p,a1+an+p+1} ={an,an+1}，an+2∈{a2+an+p,a2+an+p+1} ={an,an+1}，于是an+1,an+2∈{an,an+1} ，则a4n-1,a4n∈{a4n-2,a4n-2+1} ，又 由②知a4n-1＜a4n，则a4n-1=a4n-2，a4n=a4n-2+1，所以a3=a2=-p，a4=a2+1=1-p.由③知an+3∈{a3+an+p,a3+an+p+1} ={an,an+1} ，an+4∈{a4+an+p,a4+an+p+1} ={an+1,an+ 2} ，则an+1,an+2,an+3∈{an,an+1}，所以a5∈{-p,1-p} ∩{1 -p,2-p} ,即a5=1-p；a6∈{-p,1-p} ∩{1 -p,2-p} ，即a6=1-p；a7=a6=1-p；a8=a6+1=2-p.至此知a1=a2=a3=-p，a4=a5=a6=a7=1-p，a8=2-p，由此猜想a4n-4=a4n-3=a4n-2=a4n-1=n-1-p（n∈N*）（.说明：这里为了叙述与表达的方便，给数列{an} 增加了a0=-p）.

下面用数学归纳法证明猜想.

当n=1,2 时，猜想成立；假设n=k(k≤2，k∈N*）时猜想成立，即a4k-4=a4k-3=a4k-2=a4k-1=k-1-p，则a4(k+1)-4=a4k=a4k-2+1=k-p；由a4k+1∈{k-p,k-p+1} ∩{k-1-p,kp} ，得a4(k+1)-3=k-p；由a4k+2∈{k-p,k-p+1}∩{k-1-p,k-p} ，得a4(k+1)-2=k-p；a4(k+1)-1=a4(k+1)-2=k-p.因此当n=k+1 时猜想也成立.综上，对∀n∈N*，a4n-4=a4n-3=a4n-2=a4n-1=n-1-p.若Sn≥S10，则a10≤0 ≤a11，即2-p≤0 ≤2-p，即p=2.当p=2 时，有an＜0(n≤7),an=0（n=8,9,10,11），an＞0（n≥12），所以∀n∈N*，Sn≥S7=S8=S9=S10=S11.

综上，满足题设的实数p存在，且p=2.

评注：数列的递推关系得到前几项后，根据规律归纳猜想出通项，再用数学归纳法证明猜想，得到通项公式的方法是求解一些比较复杂的数学通项的常用方法.猜想通项公式的过程是合情推理的体现，数学归纳法证明猜想的过程是演绎推理的体现，这种解决问题的思维模式恰是发现问题、提出问题、分析问题、解决问题的过程.

3 问题的溯源

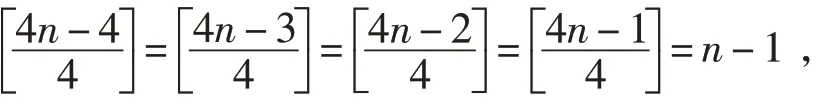
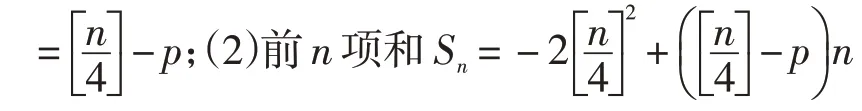
说明：命题1 是对高考题的推展，证明参照高考题的解法2，留给读者思考.

4 问题的变式

若将高考题中的“S10”改为“S11”，则有a11≤0 ≤a12，即2-p≤0 ≤3-p，即2 ≤p≤3.若p=2，当n=7,8,9,10,11 时，Sn取得最小值；若p=3，当n=11,12,13,14,15 时，Sn取得最小值；若2 ＜p＜3，当且仅当n=11 时，Sn取得最小值；照此思路，笔者编制了如下两道变式题供读者尝试.

变式1 已知数列{an} 满足：①a1≥-5，a2=-5；②∀n∈N*,a4n-1＜a4n；③∀m,n∈N*，am+n∈{am+an+5,am+an+6} .记数列{an}的前n项和是Sn，求使得Sn取最小值时的n的值.

简解：由命题得an=-5 ，则an＜0（n≤19 ），an=0（ 20 ≤n≤23 ），an＞0（n≥24），所以当n=19,20,21,22,23 时Sn取最小值.

变式2 定义Rp数列{an} 满足：①a1=-p，a3=1-p；②∀n∈N*,a2n-1＜a2n；③∀m,n∈N*，am+n∈{am+an+p,am+an+p+1} （.1）求数列{an} 的通项公式；（2）是否存在p∈R，使得存在Rp数列{an}（其前n项和是Sn），对任意n∈N*，满足Sn≥S2022？若存在，求出所有这样的p；若不存在，说明理由.

简 解：（1）an=-p；（2）a2022=1011-p，a2023=1011-p，由Sn≥S2022，得a2022≤0 ≤a2023，即1011-p≤0 ≤1011-p，即p=1011.当p=1011 时，有an＜0 (n≤2021) ，an=0（n=2022,2023），an＞0（n≥2024），所以∀n∈N*，Sn≥S2021=S2022=S2023.因此满足题设的实数p存在，且p=1011.

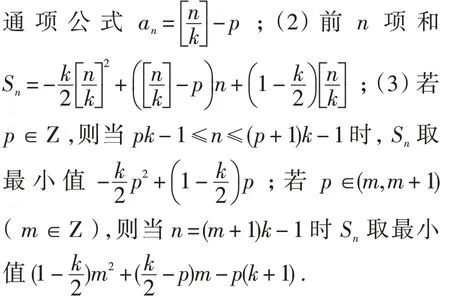
说明：命题2是对命题1的推广，证明留给读者思考.