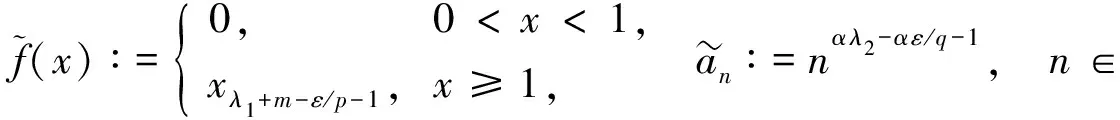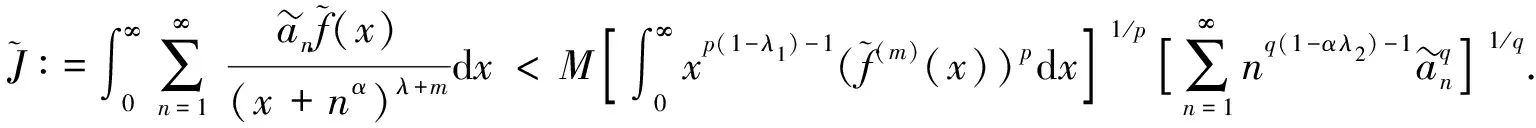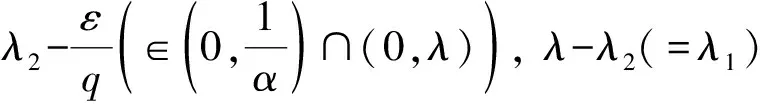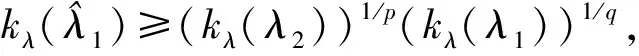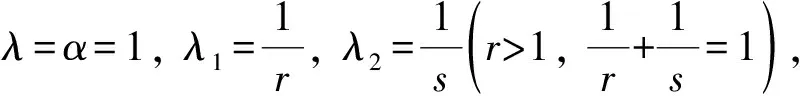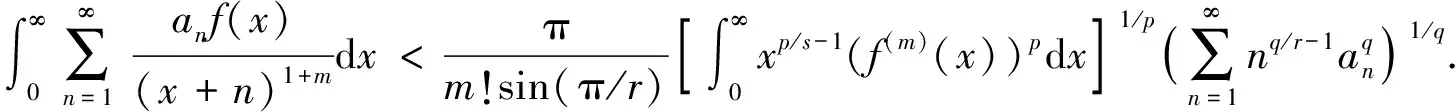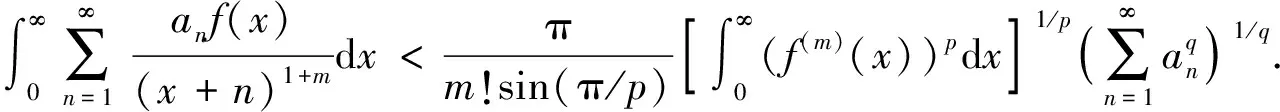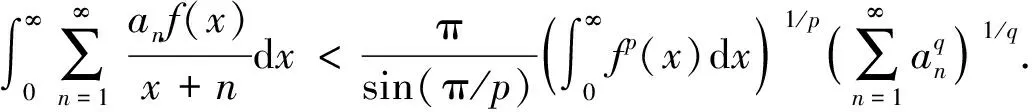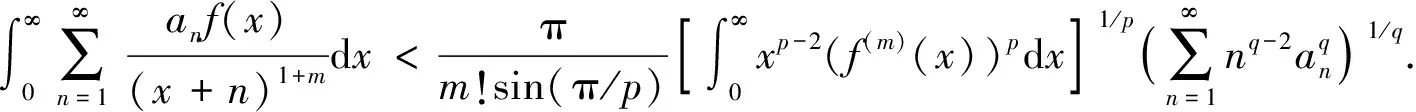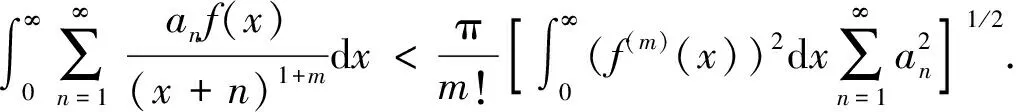一个新的涉及高阶导函数的半离散Hilbert型不等式

2022-05-30王爱珍杨必成

吉林大学学报（理学版） 2022年2期

关键词：种籽权函数吸光

王爱珍, 杨必成

(广东第二师范学院数学系, 广州 510303)

0 引言

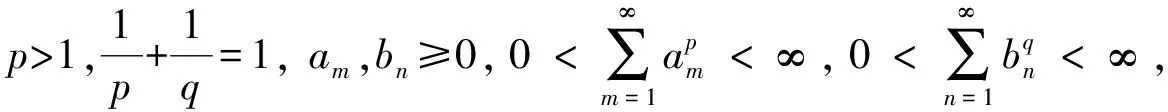
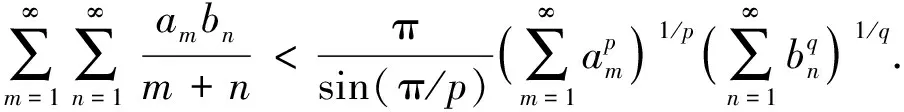
(1)

文献[2]通过引入参数λi∈(0,2](i=1,2),λ1+λ2=λ∈(0,4], 并应用Euler-Maclaurin求和公式, 建立了式(1)的如下推广式:

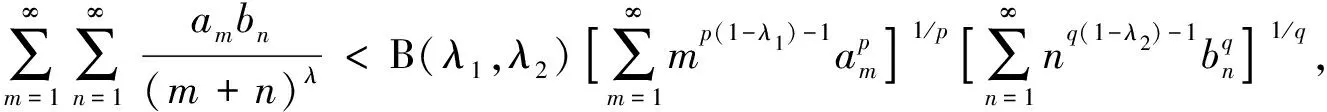
(2)

这里常数因子B(λ1,λ2)是最佳值, 且

为Beta函数.当p=q=2,λ1=λ2=λ/2时, 由式(2)可推导出文献[3]的一个结果.利用式(2)及Abel部分求和公式, Adiyasuren等[4]给出了核为(m+n)-λ涉及两个部分和的Hilbert型不等式.不等式(1)及其积分形式在分析学中应用广泛[5-15].

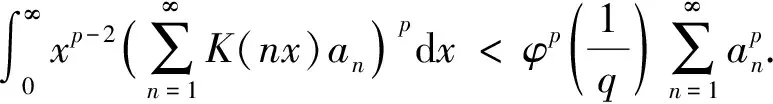
(3)

文献[16-20]给出了式(3)的应用.利用实分析技巧, 洪勇等[21]给出了式(1)推广式中最佳常数因子联系多参数的一个等价陈述; 其他类似研究结果可参见文献[22-28].文献[29]给出了逆向半离散Hilbert型不等式的一些新成果.

本文基于文献[4,21], 用权函数方法及实分析技巧, 求出一个新的核(x+nα)-(λ+m)的涉及高阶导函数的半离散Hilbert型不等式.作为应用, 讨论了不等式中最佳常数因子联系多参数的等价条件及一些特殊不等式.

1 引理

为方便, 本文设p>1, 1/p+1/q=1,m∈∶={0,1,…},α,λ>0,λ1∈(0,λ),λ2∈(0,1/α]∩(0,λ),

kλ(λi)∶=B(λi,λ-λi) (i=1,2),

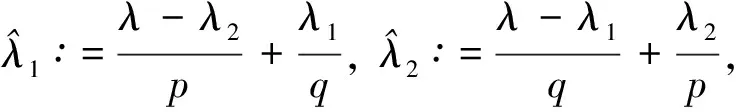
(4)

引理1定义权函数:

(5)

则有如下不等式成立:

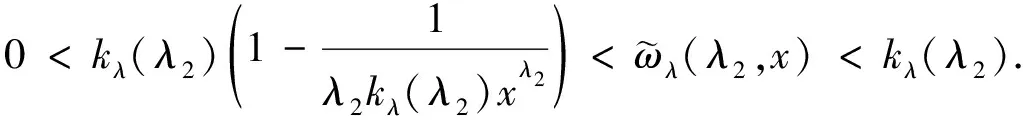
(6)

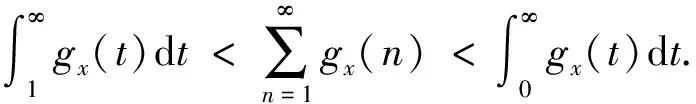
(7)

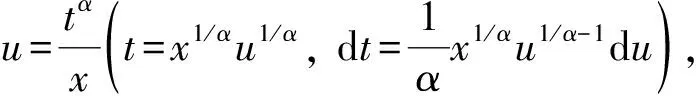
故式(6)成立.证毕.

引理2如下推广的半离散Hardy-Hilbert不等式成立:

证明: 做变换u=x/nα, 可得如下另一个权函数表达式:

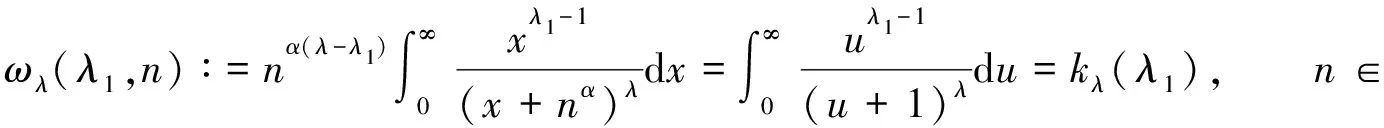
(9)

由Hölder不等式[30], 有

若式(10)中间取等号, 则存在不全为0的常数A,B, 使得

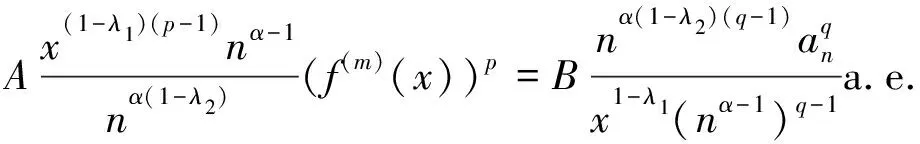
不妨设A≠0, 则存在n∈, 使得

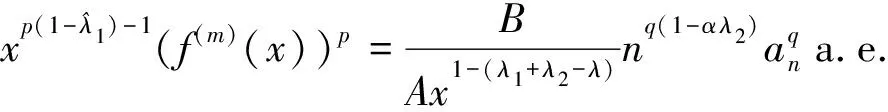
(11)

引理3对于t>0, 如下不等式成立:

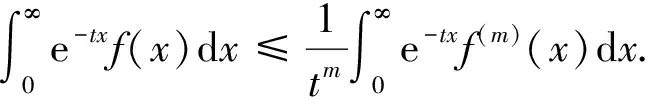
(12)

证明: 因为f(k-1)(0+)=0(k=1,2，…,m), 故由部分积分法有

迭代后可求出式(12).证毕.

注1若m=0, 则由于f(0)(x)=f(x), 式(12)取等号.

2 主要结果

定理1如下涉及一个高阶导函数的半离散Hilbert型不等式成立:

证明: 因为有

故由L逐项积分定理[31]及式(11), 有如下不等式:

再由式(8)有式(13).证毕.

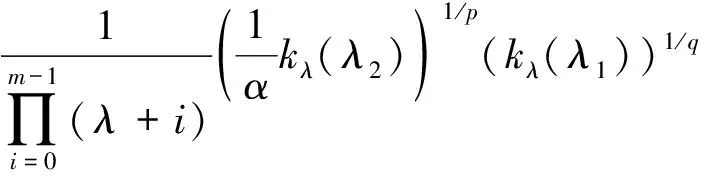
带壳、不带壳烘焙种籽衣提取液全波长扫描结果如图 5-a和图 5-b。所有样品吸收峰波长都位于274～279 nm之间。其中，未处理种籽衣提取液吸收峰波长为275.5 nm，吸光值为1.00；带壳烘焙40 min种籽衣提取液吸收峰波长为275.0 nm,吸光值最高1.13；不带壳烘焙20 min种籽衣提取液吸收峰波长为278.5 nm，吸光值为1.12。说明烘焙过程中活性成分种类以及含量是发生变化的。Alasalvar等[26]研究的榛子种籽衣提取物吸收峰波长为282 nm，说明两者活性成分较为接近。

证明: 充分性.若λ1+λ2=λ(∈(0,∞)), 对任给0<ε