近拟常曲率空间中某类紧致超曲面
2022-05-30钟家伟宋卫东
钟家伟, 宋卫东,2
(1.安徽信息工程学院 通识教育与外国语学院,安徽 芜湖 241000;2.安徽师范大学 数学与统计学院,安徽 芜湖 241000)
引言
以(Nn+1,g)表示其黎曼曲率张量,取如下形式:
KABCD=a(gACgBD-gADgBC)+b(gACfBD+gBDfAC-gADfBC-gBCfAD),∑gACgBDfABfCD=1。
(1)
的n+p维单连通完备的黎曼流形,称为近拟常曲率空间[1],其中:g是Nn+p的黎曼度量;a,b是Nn+p上C∞-函数;{fAB}是Nn+p上一个单位向量函数,称为Nn+1的生成元。
显然,当a=1,b=0时,Nn+1是单位球面Sn+1(1),文[1]给出了非常曲率空间的近拟常曲率空间的例子。对于球面Sn+1(1)上具有常数量曲率的紧致超曲面Mn,文献[2]得到了如下的刚性定理。
定理A[2]假设Mn是Sn+1(1)的紧致超曲面,其标准数量曲率R为常数,且R-1≥0,
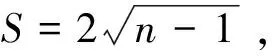
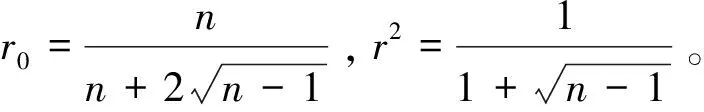
本文引入方框算子□[3],考虑近拟常曲率空间中某类紧超曲面,得到了:
定理B设Mn是近拟常曲率空间Nn+1中的紧致超曲面,若Nn+1生成元向量{fAB}沿Mn的法方向分量{fn+1A}消失,且|▽h|2≥n|▽H|2,则有如下积分不等式:
其中S表示Mn第一基本形式h模长的平方,H表示Mn的平均曲率,*1表示体积元素。
注:当Nn+1为Sn+1(1),即a=1,b=0时,若Mn的标准数量曲率R为常数,且R>1,那么|▽h|2≥n|▽H|2当然成立[2],由定理B得到刚性定理A。
1 基本公式
约定各类指标的取值范围如下:
1≤A,B,C,…,≤n+1; 1≤i,j,k,…,≤n。
在Nn+1上选取局部标准正交标架场{eA},使得限制到Mn上时,{ei}与Mn相切。以{ωA}表示{eA}的对偶标架场,{ωAB}是Nn+1的联络1-形式。限制在Mn,有[4]
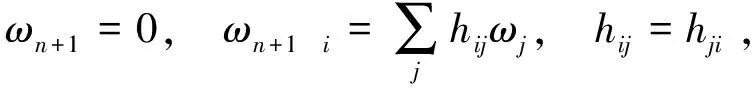
(2)
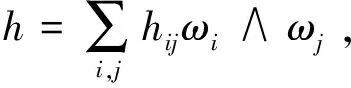
(3)
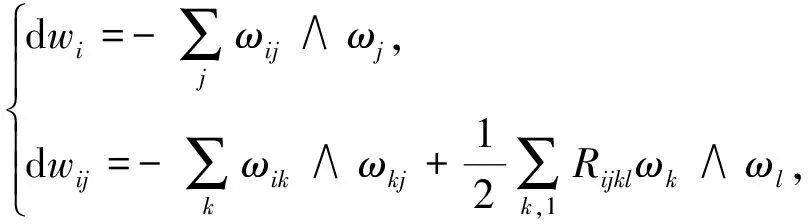
(4)
Rijkl=Kijkl+hikhjl-hilhjk,
(5)
其中Kijkl,Rijkl分别是Nn+1及Mn的黎曼曲率张量,h表示Mn的第二基本形式。又Mn的第二基本形式模长的平方S及Mn的平均曲率H分别是
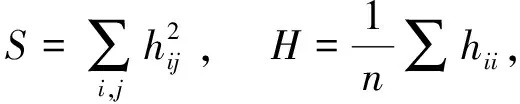
(6)
设Nn+1是近拟常曲率空间,在上述标架下,Nn+1的黎曼曲率张量可表示为:
KABCD=a(δACδBD-δADδBC)+b(δACfBD+δBDfAC-δADfBC-δBCfAD)。
(7)
假设{fn+1A}沿Mn的法向量消失,即
fn+1A=0,∀A
结合(7)式,不难得到
Kn+1ijk=0, ∀i,j,k。
(8)
以hijk及hijkl表示hij的一阶、二阶共变导数,则[4]
hijk-hikj=-Kn+1ijk,
(9)
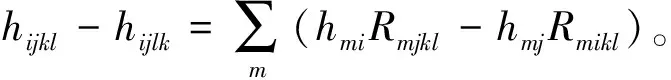
(10)
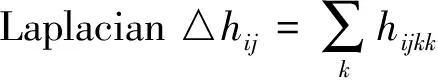
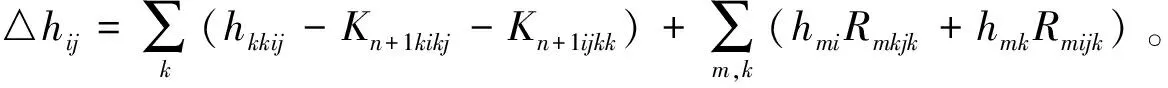
(11)
现在选取Mn的标准正交标架场{ei},使得hij=λiδij,于是
由(5)、(8)—(11)式得
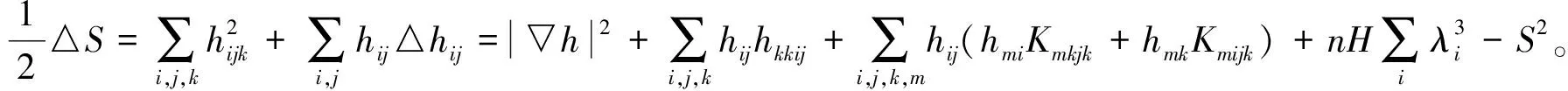
(12)
2 定理的证明
首先定义Mn上的对称张量场
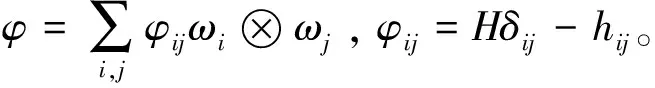
(13)
引入与φ相关的算子[4]□;∀f∈C2(Mn),
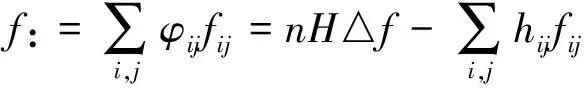
(14)
在(14)式中,取f=nH,则
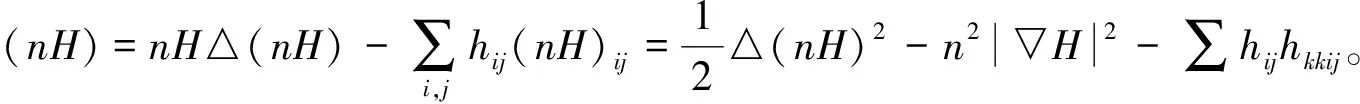
于是由(12)式得:
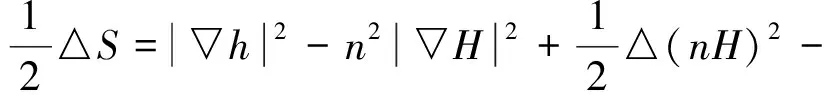
(15)
定理的证明,还需要下面引理。
引理1由公式(15)定义的算子□是一个自伴算子,即
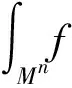
证明由(13)式,有
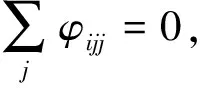
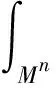
(16)
由(7)式,结合hij=λiδij,经较复杂计算,得:
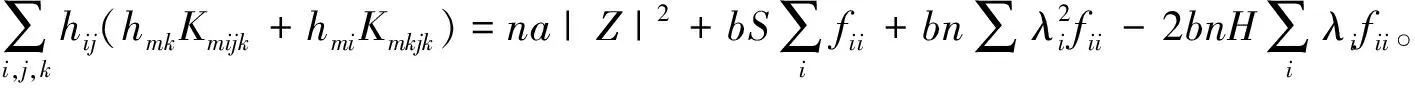
(17)
其中|Z|2=S-nH2。
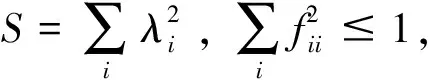
由Cauchy不等式
从而当b≥0时,由式(17)得
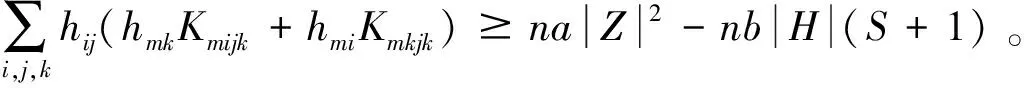
(18)
当b<0时,
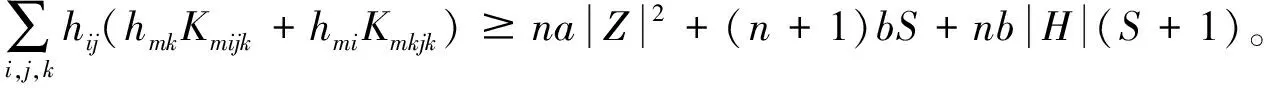
(19)
(18),(19)可统一表示为
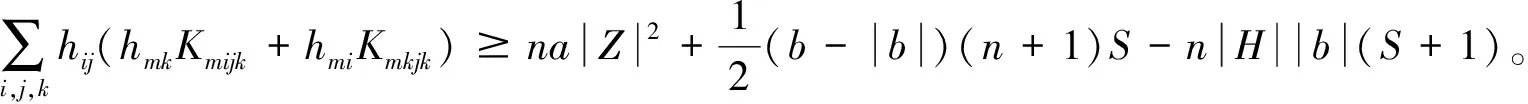
(20)
又hij=λiδij,记
于是
引理2[5]记号如上,对于n≥3,有下列不等式
等号成立当且仅当n-1个ki相等。
因此
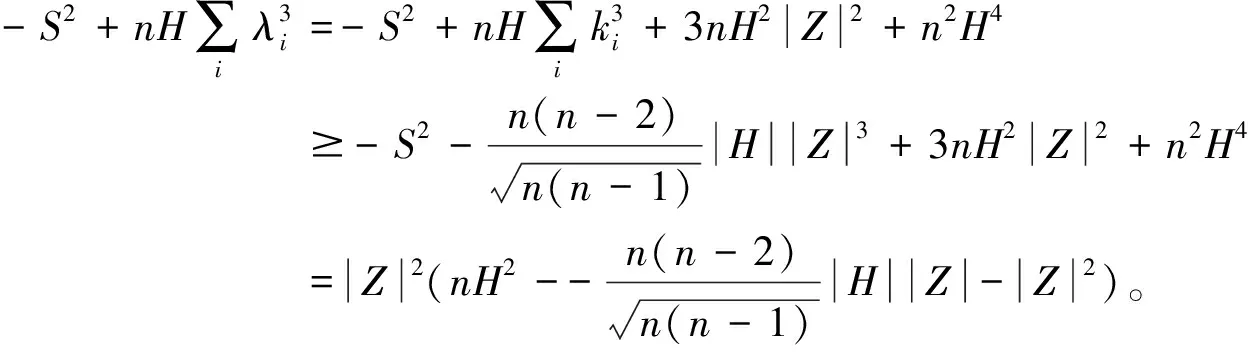
(21)

作正交变换
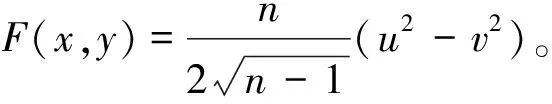
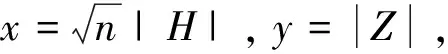
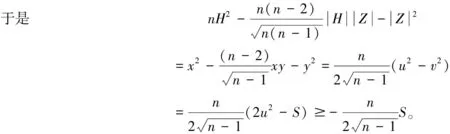
(22)
结合(21)式得:
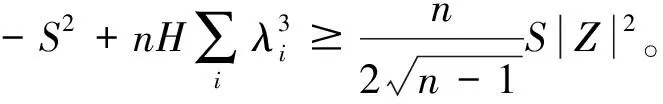
(23)
于是由(15)、(17)、(20)、(22)及|▽h|2≥n|▽H|2,有
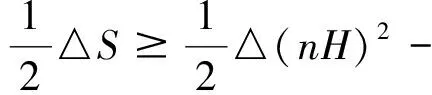
(24)
由Mn的紧性,根据Stokes定理,对(24)式两边积分,经整理,即完成了定理B的证明。
