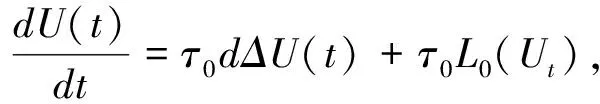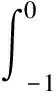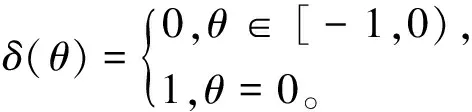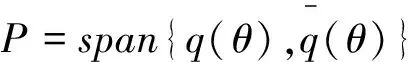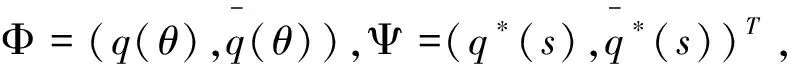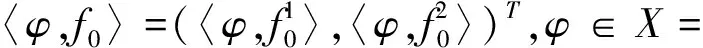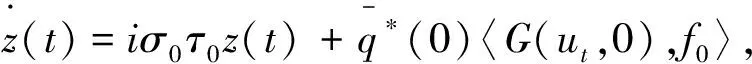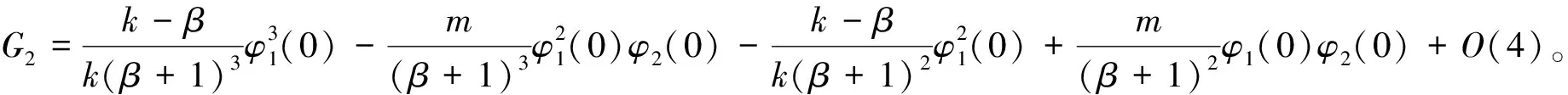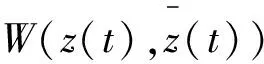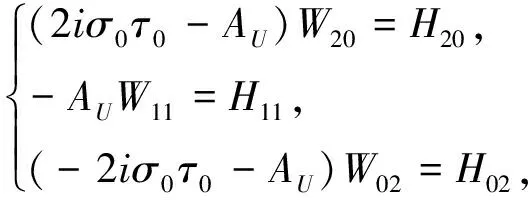一类具有时滞的捕食—食饵模型的Hopf分支
2022-05-30袁海龙
赵 童, 袁海龙
(陕西科技大学 数学与数据科学学院,陕西 西安 710021)
引言
种群模型的动力学行为是生物数学研究的一个重要内容,并且受到了学者们的广泛关注,它在生态环境保护、治理与开发等方面有着重要的作用。在生态学中,捕食者与食饵之间的相互关系由于其普遍性和重要性而长期存在,并将成为生物数学中的重要主题。随着研究的不断深入和拓展,学者们发现在自然社会中,很多现象的产生除了受当前状态的影响,还与过去的某个时刻或某个时间段的状态密切相关,这种现象称为时滞现象。由于在捕食模型中,考虑时滞效应可能会导致食饵或捕食者达到平衡状态或最终导致其中一方灭绝,因此捕食模型的时滞研究已成为当下学者关注的焦点和热点,时滞微分方程也更为广泛的应用到生物数学等领域。近年来,越来越多的学者把时滞效应引入到捕食—食饵模型中,并对其动力学行为进行了全面的研究,得到了许多结果[1-8]。
Hopf分支是时滞微分动力学中一种常见的分支现象。该现象是指研究对象的参数在某一特定值微小范围内产生变化时,模型在经过某些临界值时某些性质会发生改变,比如平衡状态改变,周期稳定性发生突变等,发生改变的相应参数的临界值被称为分支值。Yi和Wei[9]研究了一类具有齐次Neumann边界条件的捕食—食饵扩散模型
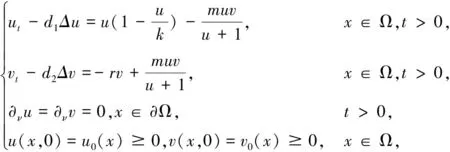
(1)
其中,u(x,t)和v(x,t)分别代表食饵和捕食者在时间t>0和空间位置x时的密度,拉普拉斯算子Δ表示种群的自由扩散效应,种群的栖息地Ω∈Rn(n≥1)是有界区域,ν是单位外法向量,d1,d2>0是物种的扩散系数,k是环境的承载能力,r代表捕食者的死亡率,m指两个物种之间相互作用的强度。更多生物意义详见[1,9-13]。文献[9]以β为分支参数,对模型(1)正常数平衡解的Hopf分支和稳态分支进行了分析,证明了在模型参数都是空间齐次的条件下多个空间非齐次周期解的存在性。
由于种群的成长期,当前时刻的种群增长率总是与某个时刻之前的种群数量有关。这种由于成长期而导致的时滞现象在种群中普遍存在,因此Chen和Shi[1]考虑给捕食者加入时滞,则模型(1)变为
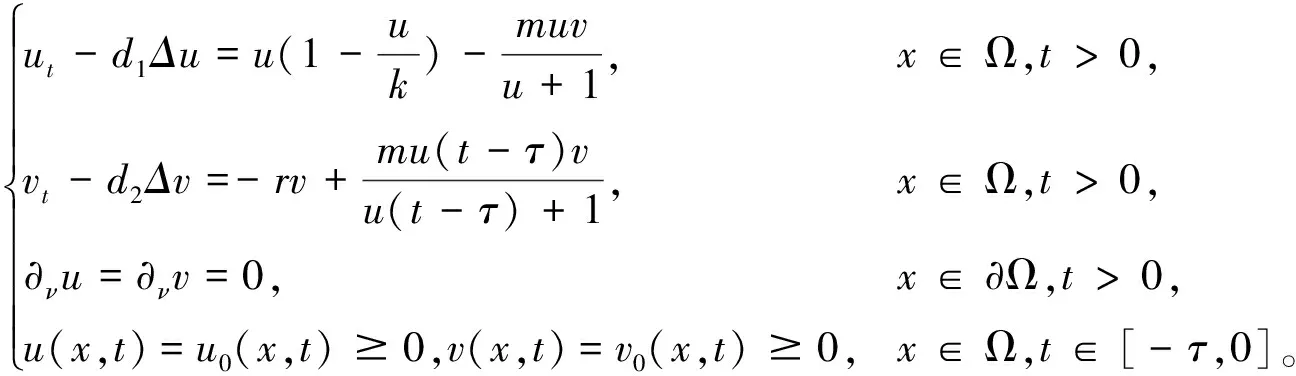
(2)

基于文献[1]的研究,考虑到捕食者和食饵均具有成长期,因此本文在模型(2)中对捕食者u和食饵v同时引入时滞,从而获得如下模型
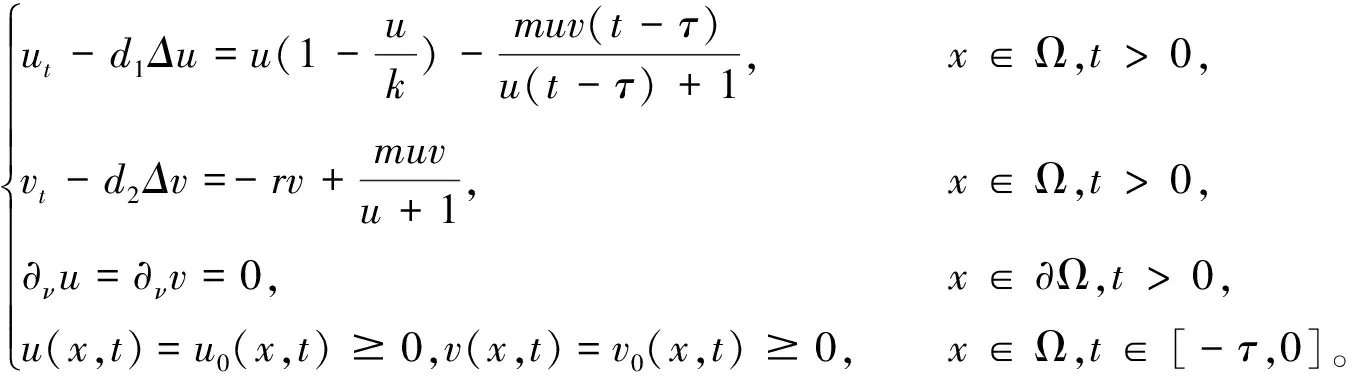
(3)
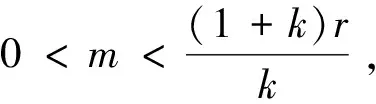

(2)0 则模型(1)的正平衡解(β,vβ)是局部渐近稳定的。本文在讨论过程中发现,若同时考虑给捕食者u和食饵v引入时滞参数,只有在情况(1)下模型(3)的正常数平衡解(β,vβ)是局部渐近稳定的,因此在本文中,只对情况(1)进行讨论。 本文的结构如下,第二部分主要讨论了模型(3)正常数平衡点的稳定性和Hopf分支的存在性。第三部分讨论了Hopf分支的方向和分支周期解的稳定性。 本小节主要分析模型(3)的正平衡点(β,vβ)的稳定性以及Hopf分支的存在性。定义 (4) 其中u=u(x,t),uτ=u(x,t-τ),v=v(x,t),vτ=v(x,t-τ)。模型(4)在抽象空间X=С([-τ,0],X)中具有如下形式的微分方程 其中dΔ=(d1Δ,d2Δ)。已知L:→X,F:→X,对于φ=(φ1,φ2)T∈X,有 其中, 模型(4)在(0,0)附近的线性化模型为 (5) 由文献[14]可知,线性模型(5)的特征方程为: λy-dΔy-L(eλ·y)=0,y∈dom(dΔ),y≠0, (6) 将 代入方程(6)中,则有 因此,方程(6)的所有特征根由以下特征方程序列给出 Δn(λ,τ)=λ2+Anλ+(Bλ+Сn)e-λn+Dn=0,n=0,1,2,…, (7) 其中, 当τ=0时,方程(7)简化为 λ2+(An+B)λ+Сn+Dn=0,n=0,1,2,…, (8) 因此,当条件H1成立时,若τ=0,则模型(3)的正平衡解E*=(β,vβ)是局部渐近稳定的。 接下来,我们将讨论时滞τ对模型(6)的正平衡解(β,vβ)稳定性的影响。假设±iσ(σ>0)是特征方程(7)的一对纯虚根,则有 -σ2+Anσi+(Bσi+Сn)e-τσi+Dn=0, 将上式的实部和虚部分离,于是 -σ2+Dn+Bσsinστ+Сncosστ=0, (9) Anσ+Bσcosστ-Сnsinστ=0。 (10) 对式(9)和式(10)分别平方后再相加可以得到 (11) 其中, 对于0 和 此外,根据式(9)和式(10),可以得到 因此,可以确定τ的表达式为 (12) 引理2.1若H1成立,则对于j=0,1,2,…,存在0 下面给出横截条件。 证明:对模型(7)两边同时关于τ求导,则有 则有, 经过上述分析,我们可以得到下面结论。 定理2.1若条件H1满足,则有 (13) 其中, G(φ,μ)=μdΔφ(0)+μL0(φ)+(μ+τ0)F0(φ), φ∈X=С([-1,0],X)。 模型(13)在(0,0)处的线性化模型是 (14) 由式(11)可知,±iσ0τ0是(14)的一对简单的纯虚特征值,其对应的泛函微分方程为 (15) 显然,L0(τ0)是映射С([-1,0],X)在X上的一个连续线性函数。根据Riesz表示定理,存在一个2×2的矩阵η(θ,μ)(θ∈[-1,0]),矩阵中的每个元素都是有界变差函数 事实上,我们有 η(θ,μ)=(τ0+μ)Eδ(θ)-(τ0+μ)Fδ(θ+1), 其中, 且对于δ(θ):[-1,0]→(X,X),有 若φ(θ)∈С1([-1,0],P2),则A(0)定义为 若ψ(s)∈С1([0,1],(P2)*),定义 A(0)和A*是双线性形式下的伴随算子 其中,ψ(s)∈С1([0,1],(P2)P*),φ(θ)∈С1([-1,0],P2)。 分别是特征值iσ0τ0和-iσ0τ0对应的特征向量,其中 线性模型(14)的中心子空间由PCN给出,其中 其中,=PCNX⊕PSX,PSX是PCNX的互补子空间。 由文献[14]知,线性模型(14)的无穷小生成元AU满足 且ψ∈dom(AU)当且仅当 由于分支方向和稳定性的计算都只与μ=0有关,在模型(13)中设μ=0,则在稳定子空间PS中可以确定一个中心 模型(13)在中心流形中的流可以写为 其中, (16) 将(16)记为 其中, (17) 定义 将其泰勒展开,则有 其中,O(4)=O(‖(u,v)‖4)。 由G(φ,0)=τ0(G1,G2)T,可得 (18) 由式(17)和(18)得 通过链式法则 我们有 (19) 对-1≤θ<0, 那么对于-1≤θ<0,我们有 由式(19)可得 当θ=0时,由式(19)和定义的AU可得 且 E1=E11·E12,E2=E21·E22, 其中, 因此,可以确定g21的表达式。 基于上述分析,能计算出每个gij。于是, 其中,μ2确定Hopf分支方向,β2确定分支周期解在中心流形上的稳定性,T2确定分支周期解的周期,由此我们可以确定分支周期解在临界值τ0处的方向和稳定性。 定理3.1对于模型(4), (2)当β2<0时,分支周期解是渐近稳定,当β2>0时,分支周期解是不稳定的; (3)当T2>0时,周期是增大的,当T2<0时,则周期是减少的。1 平衡点的稳定性和分支的存在性分析
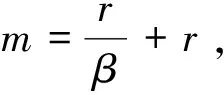




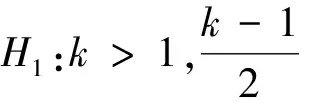

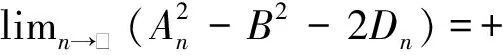
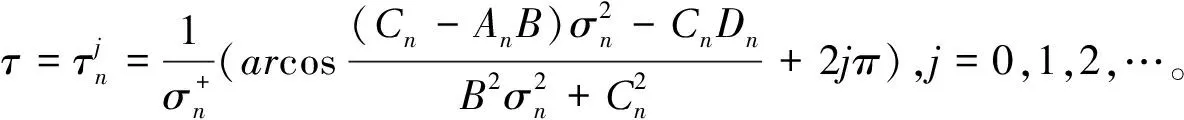





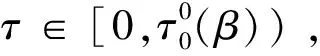

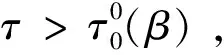
2 Hopf分支的方向和稳定性