Top-k频繁子图挖掘的差分隐私保护算法

徐 捷，杨 庚,2，白云璐,3

(1.南京邮电大学 计算机学院，江苏 南京 210046；2.江苏省大数据安全与智能处理重点实验室，江苏 南京 210023；3.南京中医药大学 信息技术学院，江苏 南京 210003)

0 引 言

由于在现实世界的应用程序中越来越多地使用图结构，图挖掘已经变得非常流行。频繁子图挖掘是图挖掘中一个重要且有趣的问题，其目标是提取给定数据集中的出现次数高于指定阈值的子图[1]。频繁子图挖掘的应用非常广泛，推荐系统就是最常见的应用，通过对浏览痕迹的挖掘，推断用户的购买意向，从而进行相关的推荐。同时，在软件工程、生物化学、金融等领域，频繁子图挖掘都有非常广阔的应用前景[2-3]。

尽管频繁子图挖掘具有很高的实际应用价值，但是在挖掘和发布子图时都存在着隐私泄露的风险[4]。假设有一个医疗保健的图数据库D，D中的每条记录表示一个用户的健康状况，子图表示某种疾病。对D进行频繁子图挖掘，挖掘结果显示了共有10个人患有肝炎。当新用户Allen的记录加入数据集D后，再次进行挖掘，肝炎患者的数量变为11，就可以推断出Allen是肝炎患者，Allen的隐私因此泄露。由此可见，频繁子图挖掘的结果不经过处理就发布很容易造成隐私的泄露，通过分析单个记录变化所引起的查询结果的变化，攻击者就可以轻易推断出用户的个人信息，这种攻击模式叫做差分攻击[4]。

差分隐私保护技术有别于传统的隐私保护技术，以成熟的概率分布知识为基础，通过添加随机噪声扰动输出结果实现隐私保护，能够有效地抵御差分攻击。在差分隐私模型下，可以通过某种差分隐私随机算法K来发布数据，并为用户提供搜索界面，该算法保证了挖掘结果不会因为数据集中任一记录的改变而受到显著的影响[5]。

目前，能够实现差分隐私保护的频繁子图挖掘算法并不多，而且这些算法难以同时满足高可用性与安全性，要么为了实现隐私保护，添加了过量的噪声，挖掘出的结果并不正确，数据的可用性大大降低；要么，隐私保护的力度不够，达不到ε-差分隐私。为此，该文提出了一种满足差分隐私的top-k频繁子图挖掘算法DP-TGM，其主要贡献如下：

(1)为了实现差分隐私保护，在算法的三个阶段都使用拉普拉斯机制给子图的支持度添加噪音，将阈值也一直更新为队列中的最小噪音支持度。

(2)为了提高数据可用性，采用均分法和特殊级数法来分配隐私预算，降低误差；同时，不断更新变大的阈值减少了子图的扩展比较次数，进一步提升准确性。

(3)理论证明，算法实现了差分隐私保护；通过对比实验，在不同规模的真实图数据集上，DP-TGM算法都展现出了更高的数据可用性。

1 相关工作

近些年来，已经有不少学者提出了满足差分隐私的top-k频繁模式挖掘算法。2012年，Li等人提出了PrivBasis算法[6]，该算法通过将输入数据投影到人们所关心的少数选定维度上来应对高维性的挑战。PrivBasis算法在高维数据集上的表现远优于TF算法，但其可用性却因随机截断引起的截断误差而大受影响。针对此问题，蒋辰等人[7]提出了TrunSuper算法，该算法使用新的截断方法，将事务中支持度较小的项剔除，通过降维减小项集的支持度误差。

在满足差分隐私的top-k子图挖掘方面，2013年，Shen等人[8]提出了一种基于采样的频繁子图挖掘算法Diff-FPM，该算法可概括为以下两个步骤：

(1)采样：使用马尔可夫链蒙特卡罗抽样(MCMC)的方法来扩展指数机制，并使用扩展指数机制直接从图数据集中选择频繁子图，重复此过程，直到获得了top-k频繁子图；

(2)扰动：对获得的top-k子图的支持度添加符合拉普拉斯分布的噪音。

然而，当样本的分布不可观察时，验证MCMC的收敛仍然是一个悬而未决的问题，Diff-FPM算法仅仅满足较弱的(ε,δ)-差分隐私。此外，算法从所有子图构成的空间中进行挑选，引入的噪音过大，数据的可用性较差。

张啸剑等人[9]提出的DP-tokP算法在差分隐私保护的模型下进行top-k频繁模式的挖掘，可用于top-k子图挖掘，其思想如下：

(1)挖掘出图数据集中所有支持度大于阈值的频繁子图，存入集合S中；

(2)设置打分函数为子图的支持度，为S中的每个子图进行打分。使用指数机制为每个子图按照分值赋予权重，并降序排列，从排列好的子图中不放回地抽取k个子图，形成最终的top-k子图集合；

(3)为挖掘出的top-k子图的支持度添加拉普拉斯噪音。

该算法同样使用了差分隐私的两种机制，满足ε-差分隐私保护。但是，在使用指数机制挑选子图之前，需要挖掘出所有的候选集，初始阈值的选择不同，候选集的个数就不同，候选集越多，产生的扰动越大，挖掘结果的准确性就越低。

以上算法在兼顾安全性和数据可用性方面依旧有很大的提升空间，难以运用于实际应用。为此，该文提出了DP-TGM算法，采用合理的隐私预算分配方法，提高数据可用性，在挖掘过程和发布数据时达到隐私保护的效果。

2 理论基础

2.1 差分隐私

定义1 近邻数据集。给定两个数据集D和D'，当且仅当两数据集之间只相差一条记录时，可称之为近邻数据集[10]。

定义2ε-差分隐私。给定两个近邻数据集D和D'，若算法A作用在数据集D和D'上的结果满足不等式(1)，则称算法满足ε-差分隐私。

Pr[A(D)=O]≤exp(ε)×Pr[A(D')=O]

(1)

不等式中，Pr[X]是事件X发生的概率，即隐私泄露的概率，它由算法A的随机属性确定。参数ε是隐私保护预算，ε值与隐私保护程度成反比，ε越小，两个近邻数据集的相同输出的概率越接近，隐私保护的程度越高。

定义3 全局敏感度。对于任意一个函数f：D→Rn，它的全局敏感性Δf定义为：

(2)

R表示所映射的实数空间，n表示函数f的查询维度。全局敏感度的大小与具体的数据集无关，由查询函数决定，反映了函数f在D和D'上变化的最大范围[11]。

添加噪声是使算法实现差分隐私保护的主要途径，最常用的噪声添加机制是拉普拉斯(Laplace)机制和指数机制，其中，拉普拉斯机制主要适用于数值型输出，而指数机制适用于非数值型输出[12]。

定义4 拉普拉斯机制。拉普拉斯机制通过在查询结果上添加满足Laplace分布的噪音来实现隐私保护。给定数据集D，若有函数f：D→Rd，其敏感度为Δf，当算法A的输出结果满足下列等式：

A(D)=f(D)+

(3)

则算法A满足ε-差分隐私，其中，Lapi(Δf/ε)(1≤i≤n)是相互独立的拉普拉斯变量。噪声大小与Δf成正比，与ε成反比。

定义5 指数机制。指数机制首先需要制定一个打分函数u:(D×O)→R,设A为指数机制下的某个算法，则输出结果为：

(4)

由公式(4)可知，分值越高，添加的噪声就越大，被输出的概率也越大。

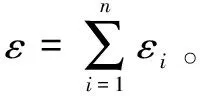
2.2 频繁子图挖掘

频繁子图挖掘是频繁模式挖掘的问题之一，其任务是找出图数据库中频繁出现的子图结构。

定义7 支持度。子图g的支持度指的是图数据库中包含子图g的记录的个数，同一记录中出现多次也只记一次，文中支持度用Sup(g)表示。

定义8 噪音支持度[12]。某一子图g在其支持度Sup(g)上添加噪音形成的支持度称为噪音支持度，如式(5)所示：

NSup(g)=Sup(g)+noise

(5)

其中，NSup(g)表示子图g的噪音支持度，noise表示添加的噪音。

定义9 频繁子图挖掘。给定图数据库D={G1,G2,…,Gn}和阈值θ，支持度大于等于θ的子图被称为频繁子图，频繁子图挖掘就是找出图数据库中所有的频繁子图。

定义10 top-k频繁子图挖掘[14]。给定图数据库D={G1,G2,…,Gn}和用户自定义值k(一般来说，k的取值较低)，top-k频繁子图挖掘就是找出图数据库中支持度排名前k的频繁子图。

3 DP-TGM算法

DP-TGM算法的挖掘对象是图数据集中支持度排名前k的子图，算法共分为三个阶段：预处理阶段、深度挖掘阶段和噪音添加阶段。

3.1 DP-TGM算法概述

算法使用两个优先级队列QK和QS，QK用来存储临时挖掘到的top-k频繁子图，噪音支持度小的优先级高；QS用来存储待拓展的频繁边，支持度高的优先级高。算法将隐私预算ε分为三份，分别用于预处理、深度挖掘和噪音添加阶段，算法1展示了算法的整体框架。

算法1:DP-TGM算法。

输入：图数据集GD；隐私预算ε；k。

输出：top-k频繁子图及其噪音支持度。

1.Initialize the priority queueQK；

2.Initialize the priority queueQS；

3.ε=ε1+ε2+ε3；

4.Pre-mining(GD,ε1)；

5.Top-k-mining(GD,ε2,QS)；

6.Add-noise(QK,ε3)；

7.returnQK。

如算法1所示：给定图数据集D，隐私预算ε和k，算法通过三个阶段的挖掘处理，最终得到top-k频繁子图集合QK。其中，预处理阶段主要用来获取频繁点和频繁边，分配隐私预算ε1；深度挖掘阶段将预处理阶段所得的频繁边进行深度挖掘，得到最终的top-k子图集合，分配隐私预算ε2；噪音添加阶段对挖掘结果的支持度添加拉普拉斯噪音进行扰动，分配隐私预算ε3。

下面将对三个阶段展开讲解。

3.2 预处理阶段

预处理阶段是DP-TGM算法的第一阶段，将图数据集进行遍历，获得频繁点和频繁边，更新QK和QS并得到新的阈值。预处理阶段的算法如下。

算法2：预处理算法Pre-mining(GD，ε1)。

输入：图数据集GD；隐私预算ε1。

输出：预处理阶段的top-k子图集合QK，QS。

1.θ=10；

2.挖掘出频繁的点和边，并存入QK中；

3.if (|QK|>k) //|QK|表示队列的大小

4. 删去QK中支持度较低的子图；

5.end if

6.依据QK对数据集GD剪枝；

7.将QK中的频繁边复制并存入QS中；

8.for each subgraph s inQK:

9.Nsup(s)=sup(s)+Laplace(|QK|/ε1)；

10.End for

11.θ=Nsup(QK.peek)；//阈值更新为QK中的最小噪音支持度;

12.returnQK，QS。

算法2是对预处理阶段的具体描述，首先设置一个较低的阈值θ(例如θ=10)，遍历数据集GD，挖掘出支持度大于阈值的顶点和边，存入QK中。若是QK中的子图个数大于k，则将支持度低的子图移出队列，依据QK进行剪枝。QS中放入QK中的频繁边，用来进行下一轮的拓展。最后将QK中的子图添加上拉普拉斯噪音，更新阈值为QK中噪音支持度的最小值。

定理1：算法2满足ε1-差分隐私。

证明：在图数据集GD中，添加或删除一条记录，对每个子图的支持度影响最多为1，所以算法2的敏感度为1。因此，如算法2的第7行所示，给QK中的每个子图添加的噪音为Laplace(|QK|/ε1)(|QK|表示队列QK的大小)，则每个子图都满足ε1/|QK|-差分隐私，由定义6可得，算法2满足ε1-差分隐私。

证毕。

3.3 深度挖掘阶段

DP-TGM算法在深度挖掘阶段有两大重要思想：

(1)不断更新阈值。在深度挖掘阶段，阈值θ随着优先权队列QK的变化而不断改变，始终将其更新为QK中的最小噪音支持度，这样可以有效地提高挖掘效率。

(2)合理分配隐私预算。隐私预算的分配涉及到噪音添加的强度，也直接影响到数据的可用性与安全性。在深度挖掘阶段，将会使用两种隐私预算分配方法：均分法和特殊级数法，对ε2进行两次分配，以更低的速度释放隐私预算，提高挖掘结果的准确性。

算法3：深度挖掘算法Top-k-mining(GD，ε2，QS)。

输入：图数据集GD；隐私预算ε2；k；算法1得到的QK，QS。

输出：top-k子图集合QK。

1.εa=ε2/|QS|；

2.whileQSis not empty：

3.g←pop the subgraph with highest priority inQS；

4.ifQKcontainsgthen

5.初始化优先权队列Q；//支持度越高，则优先级越高;

6.对g扩展，并将扩展的图存入Q；

7.for eachginQ：

9. Nsup(i)=Sup(i)+Laplace(1/εi) ;

10.` if (min(g) && Nsup(g)>θ)

11.store g intoQK；

12. if |QK|>kthen

13.QK.pop()；

14.θ=Nsup(QK.peek)；

15. end if

16. else

17.break;

18. end for

19. else

20. break;//算法结束

21.end while

22.returnQK。

算法3首先将隐私预算等分为εa=ε2/|QS|，将QS中优先级最高(支持度最高)的子图g弹出。如果QK不包含g，则算法终止，因为g是待拓展的子图里支持度最高的，而g被QK剔除，说明其支持度不够。如果QK中包含g，则将g按照最右路径规则进行拓展，并将拓展的图放入优先级队列Q中。将Q中的每个图s按特殊级数法进行隐私预算的分配，添加拉普拉斯噪声，如果噪音支持度大于θ，则将s插入QK中，然后判断QK的大小，按情况对QK进行更新，且将支持度始终设置为QK中的最小噪音支持度。若是s的噪音支持度小于阈值，则关于g的扩展结束。当QS为空时或QS中优先级最高的边都不满足要求，则算法结束，此时，QK存储的就是最终的top-k频繁子图。

定理2：差分隐私保护方法中，特殊级数法[15]采用如下预算分配方式：

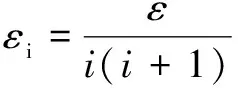
(6)

则有限次隐私预算分配满足ε-差分隐私。

证明：因为任意一次隐私预算分配量εi>0，(i∈N+)，有限次(n<∞)分配的隐私预算分配量之和为：

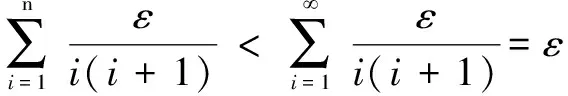
(7)

则有限次隐私预算分配ε-满足差分隐私。

证毕。

定理3：算法3满足ε2-差分隐私。

证明：算法3首先使用均分法将ε2分为εa=ε2/|QS|，QS中的每个子图得到了εa的隐私预算。算法依次将QS中优先级最高的子图g移出队列，进行深度挖掘，使用特殊级数法进行隐私预算分配，由定理2可得，每个子图g的深度挖掘满足εa-差分隐私。又由定义6可得，整个算法2满足εa×|QS|=ε2-差分隐私保护。

证毕。

3.4 噪音添加阶段

噪音添加阶段是DP-TGM算法的最后一个阶段，主要思想是对挖掘出的top-k频繁子图的真实支持度添加拉普拉斯噪声进行扰动。

算法4：噪音添加算法Add-noise(QK，ε3)。

输入：算法2得到的QK，隐私预算ε3。

输出：加噪后的top-k子图集合QK。

1.for subgraphGiinQK:

2.εi=ε3/k;

3.Nsup(Gi)=sup(Gi)+Laplace(εi);

4.end for

5.ReturnQK。

定理4：算法4满足ε3-差分隐私。

证明：这里使用均分法将隐私预算均分为k份，QK中的每个频繁子图添加的噪音为Laplace(k/ε3)。算法4和算法2一样使用均分法来分配隐私预算，所以同理可证，算法4满足ε3-差分隐私。

证毕。

3.5 DP-TGM算法隐私性证明

定理5：DP-TGM算法满足ε-差分隐私保护。

证明：DP-TGM算法将隐私预算分为三份，分别用于三个阶段：预处理(ε1)、top-k子图挖掘(ε2)、噪音添加(ε3)。该文设定隐私预算的分配比例ε1:ε2:ε3=1∶5∶4。由定理1可得，算法1满足ε1-差分隐私，由定理3可得，算法2满足ε2-差分隐私，由定理4可得，算法3满足ε3-差分隐私。由定义6差分隐私的序列组合性可得，算法满足(ε1+ε2+ε3)-差分隐私保护，而DP-FGM算法的整体隐私预算ε=ε1+ε2+ε3，所以DP-FGM算法满足ε-差分隐私保护。

证毕。

4 实验结果与分析

本节将通过对比实验来验证算法的数据可用性。实验环境为 Inter(R) Core(TM) i5-8250U CPU @1.60 GHz，8.00 GB内存Windows10 64位操作系统。

实验将在三个真实的图数据集上进行测试，分别是NCI1、Protein和Reddit-multi。NCI1是抗非小细胞肺癌和卵巢癌细胞系活性筛选的化合物数据集，Protein是蛋白质分子结构数据集，Reddit-multi则是社交网络数据集。表1展示了各数据集的具体特征，包括图的个数(graph count)，平均节点数(avg-nodes)和平均边数(avg-edges)。

表1 图数据集信息

该文将DP-TGM算法与DP-tokP算法和Diff-FPM算法进行比对，实验所涉及的代码均由java语言实现。由于噪声的加入，数据具有随机性，实验结果存在不确定性，因此采取多次试验取平均值的方式来记录结果。

4.1 度量指标

该文使用两个度量标准：F1-Score和RE。F1-Score主要衡量挖掘的频繁子图结果的可用性，RE则用来衡量子图支持度的准确性。F1-Score的比较结果使用条形图展示，而RE的比较结果用折线图展示。

定义11 F1-Score[16]：

(8)

其中，Accuracy表示精确率，Recall表示召回率。Accuracy=(Up∩Us)/Up，Recall=(Up∩Us)/Us，Up是在差分隐私下进行频繁子图挖掘的结果，Us则是频繁子图挖掘的准确结果。F1-Score将精确率和召回率综合考量，取值区间为[0,1]，F1-Score的值越大，则代表数据效用越好。

定义12 RE(相对错误率)：

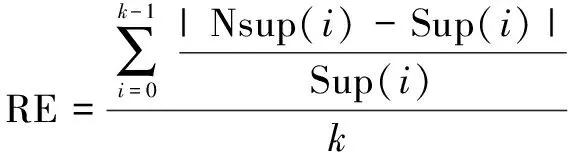
(9)

式中，Nsupv(i)(0≤i≤k-1)是结果集中第i个子图的噪音支持度，Sup(i)则是第i个子图的真实支持度。RE用来衡量挖掘到的频繁子图的支持度的错误率，取值区间为[0,∞]。RE的值与引入的噪音量大小相关，噪音越大，噪音支持度与真实支持度的差值越大，RE的值就越高，数据可用性就越差。所以，RE的值越小，算法的数据效用越高。

4.2 可用性随k取值的变化

DP-TGM算法是进行top-k频繁子图挖掘的算法，k的大小将影响隐私预算的分配。实验通过调整k的大小来对比三个算法的F1-Score和RE值。这里，统一设置隐私预算ε为1，k从30变化到150，间隔为30，在三个数据集上进行测试，结果如图1～图3所示。随着k的变大，三个算法的F1-Score都在降低，而RE值在增大，说明随着k增大，算法的数据效用在降低。而当k相同时，DP-TGM算法的F1-Score始终要比DP-tokP算法和Diff-FPM算法高，而RE要比它们低，验证了DP-TGM算法的优越性。

图1 数据集NCI1随k变化时可用性变化情况

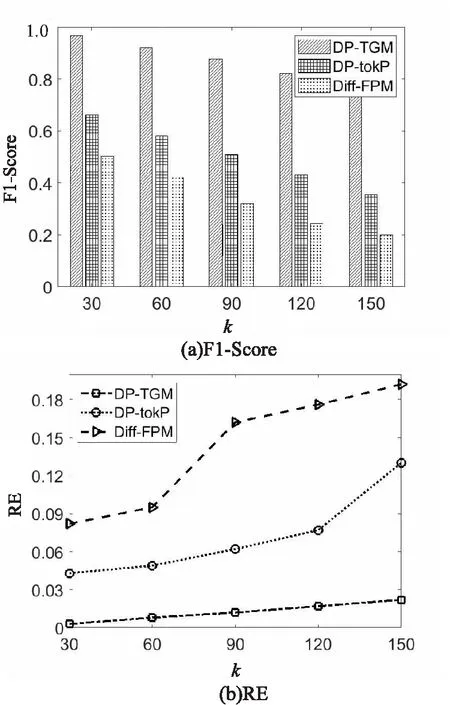
图2 数据集Protein随k变化时可用性变化情况

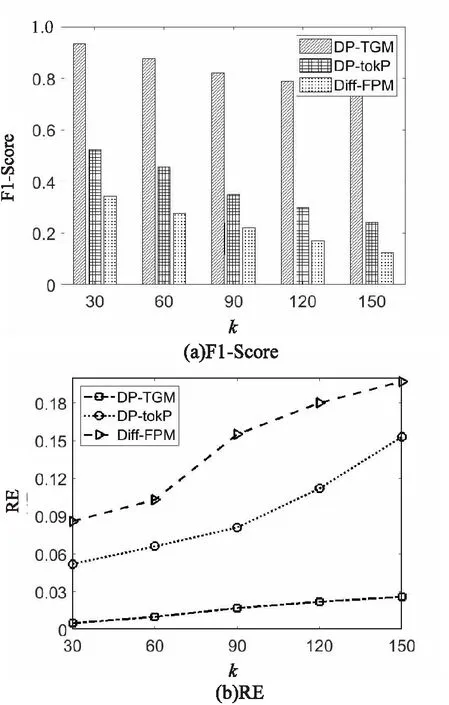
图3 数据集Reddit-multi随k变化时可用性变化情况

4.3 可用性随隐私预算ε取值的变化

隐私预算ε的取值可以影响到噪声的大小，而每个算法隐私预算的分配也不相同，所以ε的变化会影响挖掘结果的数据效用。这里统一设置k为50，ε从0.5变化到1.5，间隔为0.25，在NCI1和Protein两个数据集上进行测试，实验结果如图4、图5所示。

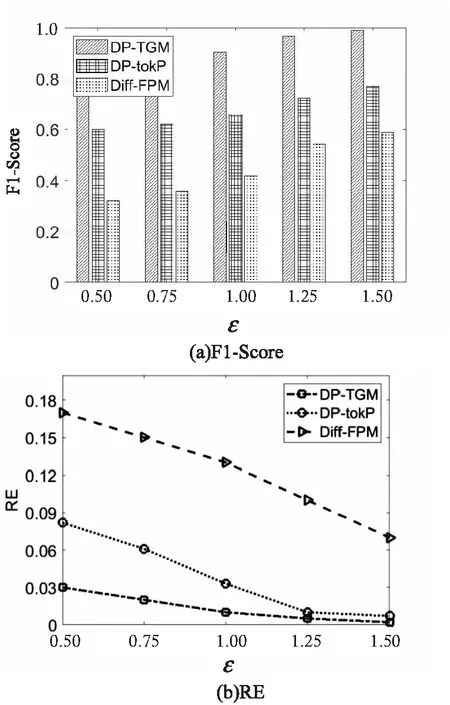
图4 数据集NCI1随ε变化时可用性变化情况

图5 数据集Protein随ε变化时可用性变化情况

随着ε的增大，三种算法的F1-Score值都在增大，而RE值在减小，这是因为ε的增大，引入的噪音减小，提高了数据效用。而在ε从0.5变化到1.5的过程中，DP-TGM算法的F1-Score值始终最高，RE值始终最低，再次验证了文中算法的优越性。

5 结束语

设计并实现了一个满足差分隐私的top-k子图挖掘算法DP-TGM，通过不断地更新优先权队列QK，将不满足要求的子图剔除，同时更新阈值，提高挖掘的效率。为了提高数据的可用性，使用均分法和特殊级数法进行隐私预算的分配，以更低的速度释放隐私预算。同时，在不同规模的真实图数据集上的测试成果也显示了算法具有更高的数据可用性。为了提高挖掘性能和结果的准确性，在挖掘子图的过程中浪费了一些隐私预算，因此下一步将研究如何减少隐私预算的浪费。