数字趣谈：道生一，一生二

刘瑞祥

1是自然数的单位。经常有人问，0是不是自然数？答案是，你可以认为它是，也可以认为它不是。按现代数学的观点，“自然数”就是符合“皮亚诺公理”的数。根据该公理的表述“要有一个自然数，每个自然数要有一个后继，不同的自然数的后继不一样”，你可以把最开始的那个自然数定为1或者0，这对后面的研究没有什么影响。如果怕产生歧义，可以进行说明，例如“本书（或本文）所讲的自然数，包括（或者不包括）零”。

1看似简单，在英国数学家罗素和怀特海的巨著《数学原理》里直到第363页才有了一个关于1的定义，而1+1（就是小学算术里的1+1，不是哥德巴赫猜想）则是在第379页才有了答案。即使在数学外行能理解的范围里，1的内容也很丰富，比如1是乘法的单位元，即任何数和1相乘结果不变。再比如，前文说的“后继”，就是指每个自然数后面有唯一的一个数，也就是说每个自然数加上1就得到下一个自然数。

在解析几何里，一次方程是最简单的直线或者平面，也叫作线性方程。行列式、矩阵这些更复杂的数学概念都和一次方程有着密切的联系，而微积分的基本思路就是以直代曲。

万丈高楼平地起，再伟大的事业也要从“一”开始，万里长征是一步步走出来的，谁也不能一口吃成胖子。

有時候，老师会对学生说：“有一就有二，你这次忘写作业，下次还会忘。”的确，很多人第一次做了错事后又做了第二次，于是陷入泥潭不能自拔。

在哲学上，到底应该“一分为二”还是“合二为一”是个问题。《易经》上说“无极生太极，太极生两仪”，于是有了万物。

“两点确定一条直线”是最简单的几何公理。在现代数学中，公理是指一种约定，或者说是对基本概念的定义。这条公理是说，如果有两个“东西”，“东西A”能决定另外一种“东西B”，那不妨就把A看作点，把B看作直线。你可以把球队看作点，把比赛看作直线，在计算10支球队能打多少场不同比赛的时候，是不是和计算10个点能形成多少直线的方法一样？

牛顿的力学体系中，只要谈到“力”，一定涉及两个物体——施力物体和受力物体。但牛顿力学只适用于“惯性系”，如果在非惯性系里应用牛顿定律，就要加上“惯性力”。这其实是个假想出来的力，只有受力物体没有施力物体。爱因斯坦看到了惯性力和万有引力之间的联系，建立了广义相对论。

根据开普勒行星运动定律，行星轨道为椭圆，而椭圆有两个焦点，其中一个是太阳所在的位置，那么另外一个焦点有什么特殊之处吗？直到现在科学家还没有找到规律。

单独的氢原子、氧原子不能稳定存在，必须达到两个才行。

单独一个点电荷产生的电场，场强和距离的平方成反比，电势和距离的一次方成反比，二者都是对电场的完整描述。

“二”在数学上的意义“一言难尽”。

众所周知，曲线的一阶导数对应着切线斜率，二阶导数对应着凹凸性。二次方程、二次函数是初中数学的重点和难点，也是走向更高深数学的起点，比如二阶线性微分方程就和二次方程有着密切的联系。

圆锥曲线，即二次曲线，是行星天文学的基础。早在古希腊时期，就有学者仔细研究了圆锥曲线，并将其系统化。阿波罗尼奥斯的《圆锥曲线论》诞生的时候还没有坐标系和完备的数学符号，完全用纯文字的方式清晰地叙述各个命题，单凭这一点就让人佩服。据说古希腊语非常严谨，仅定冠词就有20多个。直到笛卡尔建立解析几何后，《圆锥曲线论》的成就才被超越。数学上关于“二”的最高成就也许是高斯创造的，他在经典著作《算术探索》里仔细研究了二次同余方程和二次不定方程。

看不懂这两本深奥的学术著作也没关系，经典本来就不容易读懂，但可以从一个看得懂的问题入手了解“二”。例如，将线段、角和圆弧二等分很容易，这些作图方法用不着平行公理，也就是说在任意空间里都能进行，而且既然能二等分，自然也可以四等分、八等分乃至十六等分，1/2+1/4+1/8+1/16……的极限是1。或者说，我们先对一个量取它的一半或更多，然后再取剩余的一半或更多，这个过程一直进行下去，最后剩余的就会少于任意事先给定的量。《几何原本》里用这个方法证明了圆的面积和半径平方成正比、棱锥体积是等高棱柱体积的三分之一、球的体积和半径的三次方成正比，这就是所谓的穷竭法，证明过程极其美妙。

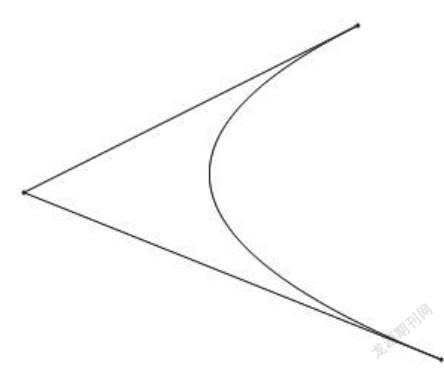
计算机和“二”的缘分颇深，先讲一个比较具体的问题。计算机绘制曲线的基本工具是“贝塞尔曲线”，其中最简单的是二次贝塞尔曲线：给出三个点，其中两个是曲线端点，另外一个是两个端点处切线的交点，就可以用二次参数方程描述这个曲线了，计算起来非常简单。

计算机和“二”更紧密的联系是计算机采取二进制。二进制“逢二进一”，大大简化了电路设计，由此导致各种存储器的容量都用2的若干次幂为单位。在计算机汇编语言中，一个单片机采集256个数据，然后计算平均值，只需要把这些数都加起来然后舍弃最低的字节（相当于除以256并舍弃余数）就可以了。同时，我们要注意，计算机不但是计算工具，更是逻辑机器。经典的逻辑是二值逻辑，“是”和“非”不容模糊，逻辑学中的排中律、矛盾律都与此相关。

有人说二进制是伟大的发明，其实如果不是误打误撞地遇到了计算机，二进制没有什么实用价值。也有人说，中国古代的阴阳或者八卦就是二进制，对数学的发展有重要贡献，这是一种误解。古代的一些算法可能对数学家莱布尼兹产生过一些启发，但阴阳也好，八卦也好，都不是形式系统。

1和2是每个孩子最早接触的数字，它们开启了数学启蒙的大门，也开启了用数学构建世界的认知之旅。1和2像一对好兄弟，它们既简单又复杂，既浅显又深邃，“道生一，一生二”，智慧与万物初现，世界由此展开……