平纹编织面板泡沫夹芯结构修补后侧向压缩有限元渐进失效分析

王轩 冮庆庸 张世秋

摘要：为研究修补对平纹编织面板泡沫夹芯结构侧向压缩性能的影响，通过USDFLD材料子程序，设置Tsai-Wu准则面板材料的失效判据，将线性屈曲模态考虑为初始缺陷，建立平纹编织面板泡沫夹芯结构修补后侧向压缩渐进损伤失效分析模型。结果表明，所建立模型的有效性通过试验得到了验证；面板挖补倾角在1∶10～1∶22范围内修补质量较好，且侧向压缩强度随面板挖补倾角比例的减小而增大；附加层重叠宽度在5～15mm范围内修补质量较好，且侧向压缩强度随附加层重叠宽度的增大而减小，但变化幅度不大；对完好泡沫夹芯结构或者母板损伤小的修补件，纯屈曲分析方法对其最大侧向压缩载荷的预测更加准确；夹芯结构侧向压缩的失效机理为芯材首先发生失效，然后面板发生局部屈曲，当载荷达到试件侧向压缩强度后，面板最终失效。

关键词：平纹编织；复合材料；修补；泡沫夹芯；侧向压缩；渐进失效分析

中图分类号：TB332文献标识码：ADOI：10.19452/j.issn1007-5453.2022.04.011

基金项目：航空科学基金（2018ZF67011）

民用飞机机载雷达罩常以玻璃纤维平纹编织材料为面板，以聚甲基丙烯酰亚胺泡沫（PMI泡沫）为芯材，与传统的蜂窝夹芯结构相比，泡沫夹芯结构具有密封性好、整体成形工艺易实现等优点[1]。由于复合材料面板较薄，夹芯结构在使用过程中易受到面外冲击而损坏，需要修补来恢复其性能。由于雷达罩结构常处于侧向受压状态[2]，故研究平纹编织面板泡沫夹芯结构修补后侧向压缩性能具有重要的工程价值。

国内外很多学者都对复合材料修补结构进行了仿真分析研究。张铁纯等[3]总结了挖补修理复合材料夹芯结构侧向压缩性能的研究现状，分析了材料、工艺、构型及环境等影响因素，指出最新的修补建模方法和力学试验结果分析思路。李剑峰等[4]在对蜂窝夹芯结构单面贴补弯曲性能研究中，建立了修补结构的三维有限元模型，分析结果表明，随着补片的直径和厚度的增加，修补结构的承载能力呈现出先增加后减小的趋势。刘国春等[1]建立了泡沫夹芯修补结构有限元分析模型，结合夹芯结构的稳定性理论，认为复合材料夹芯修补结构的主要侧压破坏模式为面板一阶與二阶屈曲失效。T. Zhang等[5]对蜂窝复合材料的开孔损伤与修补后侧向压缩进行了准静态模拟，考虑了层内损伤、层间分层和蜂窝状损伤，研究了不同挖补倾角比例、不同铺层顺序和不同附加层数量对挖补夹芯板的极限强度和应力分布的影响。王跃全等[6]建立了复合材料层合板贴补结构的渐进损伤三维有限元模型，发现相同的补片搭接宽度，损伤面积越大的层合板修补强度越低。R.D.S.G.Campilho等[7]利用ABAQUS中的cohesive单元模拟胶层的力学行为建立了有限元模型，对斜接修补的胶结接头进行纯压缩屈曲验证研究，试验结果证明模型是有效的。邓健等[8]基于非线性有限元方法，研究了双面贴补复合材料层合板的压缩屈曲强度和损伤演化过程，发现补片尺寸较大时，胶结修补区域的外部产生局部屈曲现象。白瑞祥等[9]利用有限元软件ANSYS建立有限元模型，对受载裂纹损伤结构的复合材料胶结修补效果进行了断裂力学分析，发现增加补片的刚度和增加胶层的弹性模量均会降低裂纹尖端的应力强度因子。程起有等[10]开展了复合材料层合板胶结修补参数优化研究，采用改进的BP神经网络建立参数优化预测模型，试验结果表明模型有较高准确性。吕胜利等[11]对复合材料单面胶结修补结构建立了分析模型，利用该模型研究补片参数对胶结修补效果的影响，得到优化后的补片参数。

在夹芯结构的压缩性能仿真研究方面，王宝芹等[12]基于改进通用单胞模型预测蜂窝夹芯结构的压缩失稳载荷和损伤破坏载荷，并发现蜂窝夹芯结构破坏模式为先发生屈曲失稳，然后迅速破坏。刘智良等[13]对含有分层缺陷的蜂窝夹芯结构建立了子层局部屈曲模型，结果表明当分层形状及其大小不同时，夹芯板表现出不同的破坏机制。万玉敏等[14]通过有限元方法对蜂窝夹层复合材料结构的面内压缩整体屈曲开展研究，分析了典型薄壁夹层结构的承载能力和破坏模式。陈悦等[15]基于非线性屈曲理论，利用三维内聚力单元模拟面芯分层并引入初始预变形及材料损伤判据，发现结构首先出现的破坏模式为面芯脱胶分层破坏，与试验现象吻合，轴压极限承载的试验和仿真结果最大误差为9.04%，证明了该方法预报极限承载的可靠性。L. Fagerberg等[16]在对夹芯结构的压缩研究中，发现由于由初始缺陷引起的变形会产生较大的局部应变，引发材料失效，这是强度问题，而不是稳定性问题，所以建议在夹芯结构的压缩强度计算中考虑初始缺陷。曹景斌等[17]研究了湿热条件对于层压结构压缩强度和蜂窝夹层结构侧压强度的影响，发现湿热环境是造成结构承载能力下降的重要因素。综合上述文献发现复合材料层合板修补的仿真研究方面已经有了许多成果，蜂窝夹芯结构较早用于航空航天领域，其力学性能研究成果也有不少。但关于泡沫夹芯结构的压缩性能研究尚少，因此本文通过建立修补后的平纹编织面板泡沫夹芯结构的渐进损伤失效分析模型，对其侧向压缩性能进行研究。

首先建立了基于Tsai-Wu失效准则的平纹编织面板泡沫夹芯结构渐进损伤有限元分析模型，该模型通过芯材与面板共节点建模的方法，实现结构的连续损伤，通过屈曲分析引入模型线性屈曲模态的位移，乘以一个比例因子（夹芯板厚度1%）作为模型的初始缺陷，再利用ABAQUS隐式求解器中的静态Riks方法进行侧向压缩强度分析，研究修补参数对平纹编织面板泡沫夹芯结构侧向压缩强度和破坏模式的影响，并与试验结果对比，验证模型有效性。

1试验

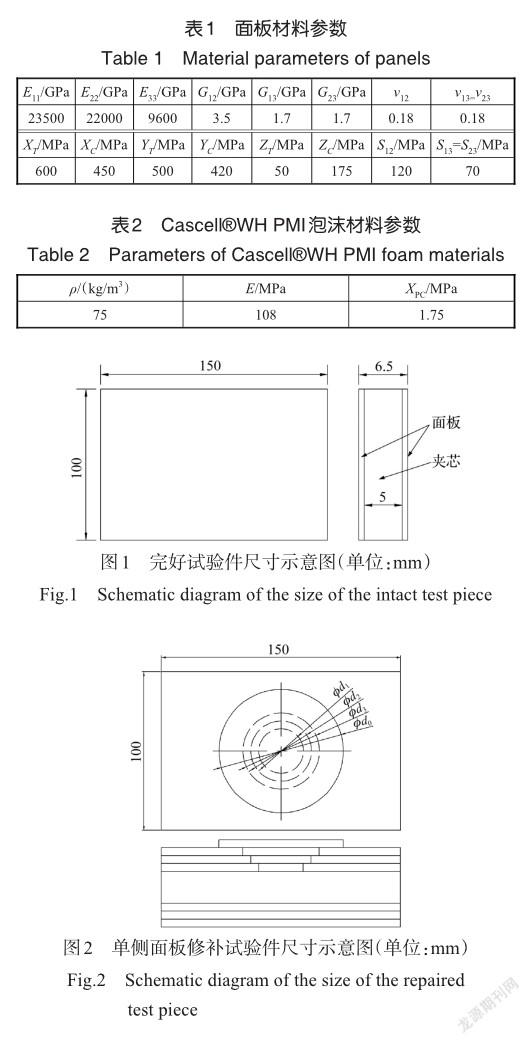
侧向压缩试验件面板的材料是平纹编织玻璃纤维3218/SW280A，材料参数见表1，表中的E11、E22和E33为弹性模量，G12、G13和G23为切变模量，ν12、ν13和ν23为泊松比，S12、S13和S23为剪切强度，XT为1方向拉伸强度，XC为1方向压缩强度，YT为2方向拉伸强度，YC为2方向压缩强度，ZT为3方向拉伸强度，ZC为3方向压缩强度。面板为三层平纹编织预浸料固化制成，厚度0.75mm。芯材的材料为PMI泡沫Cascell？WH，厚度为5mm，厂家提供的材料参数见表2。表2中，ρ为泡沫密度，E为泡沫弹性模量，XPC为泡沫压缩强度。平纹编织面板泡沫夹芯完好试验件的长宽高分别为150mm、100mm和6.5mm，面板由三层单板组成，每层0.25mm，尺寸如图1所示，单侧面板修补后试验件的尺寸如图2所示，附加层厚度为0.25mm，图中的？d1，？d2，？d3分别为第1～3层圆形补片的直径，？d0为圆形附加层的直径。

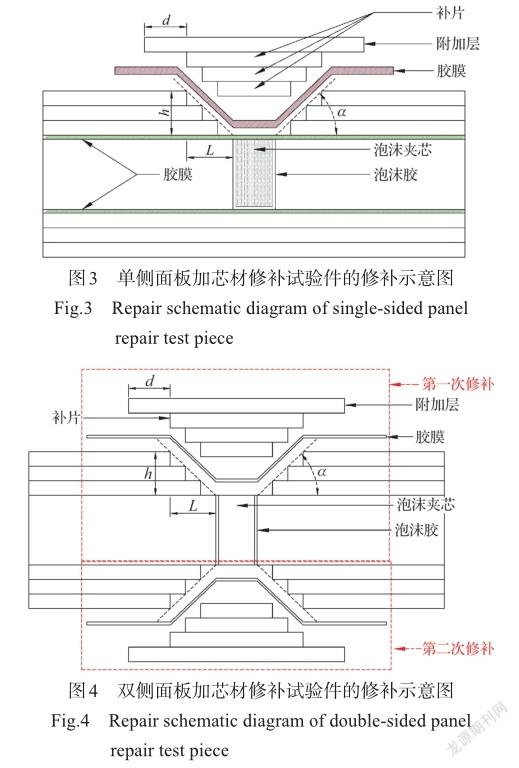
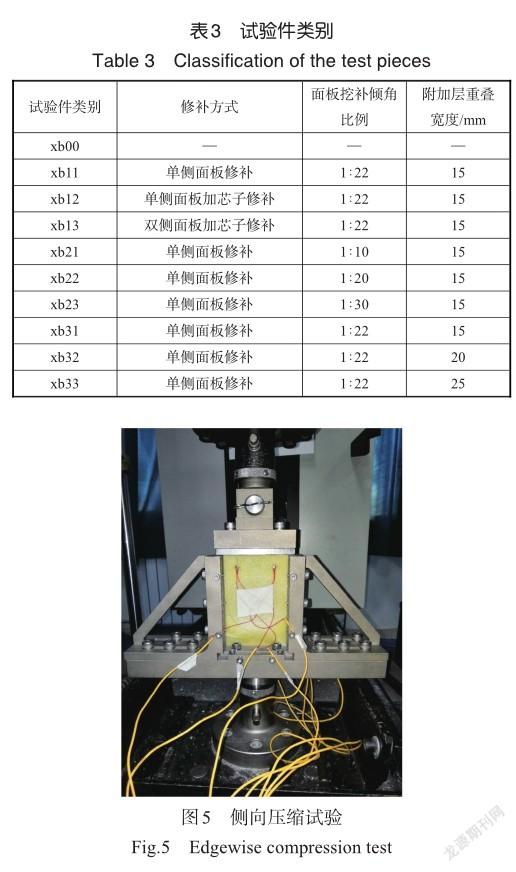
为了清楚地显示修补参数和修补结构，以单侧面板加芯材修补试验件为例，在中部横截面处绘制修补示意图，如图3所示。图中，d为附加层重叠宽度，h为泡沫夹芯结构单侧面板厚度，也是挖补的厚度，α为面板挖补倾角，本文中的挖补倾角比例的值为h/L。双侧面板加芯材修补试验件中部横截面修补示意图如图4所示。各组试验件编号对应的修补方式及修补参数见表3，每个组有6个试验件。

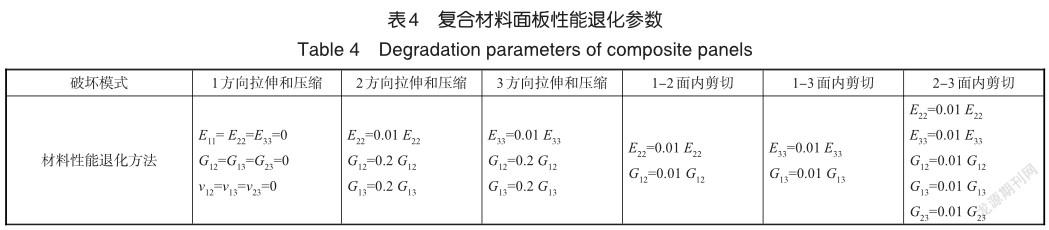
根据美国材料与试验协会（ASTM）D7137标准进行侧向压缩试验，压缩试验在Instron 5892型万能材料试验机上进行，试验机压头加载速度为1.25mm/min，具体试验条件如图5所示。万能材料试验机内置计算记录软件，试验结束后可以获得压头在压缩过程中所受力与位移曲线、压缩强度和应力应变曲线等相关记录。

2渐进损伤失效模型

对试验现象观察可发现，在泡沫夹芯结构修补后侧向压缩过程中，结构会出现面板损伤和芯材损伤。故选取连续介质损伤力学模型和可压碎泡沫（crushable foam）模型分别模拟复合材料面板和芯材的损伤。

2.1面板损伤模型

林国伟等[18]在复合材料后屈曲分析失效准则适应性研究中，发现不区分失效模式的Tsai-Wu失效准则在计算结果精度上比区分失效模式的Hashin准则、Puck准则和ChangChang准则要稍高，侧向压缩仿真的主要目的是预测较为精确的侧向压缩强度，故采用Tsai-Wu失效准则作为面板材料的失效准则，Tsai-Wu失效准则具体形式如式（1）和式（2）所示[19]。复合材料面板性能退化具体参数见表4[20]。

3有限元建模

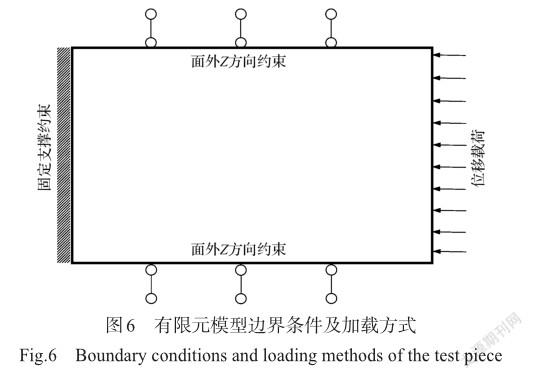
对试验件边界条件与加载方式进行简化处理，模型右侧面约束所有6个自由度方向，设置为固支，对模型上下两个侧面约束Z方向的面外位移，在模型左侧面选取中部一个节点作为参考点，将参考点与左侧面上的所有节点的相互作用设置为梁类型的多点约束，便于在参考点施加集中力或位移载荷，约束参考点除X方向外所有5个自由度方向，有限元的模型边界条件示意图如图6所示。

根据前期已发表论文试验结果发现[23]，不论是完好试件还是修补试件，在侧向压缩试验过程中均没有发现补片脱黏、面芯脱胶、面板分层等胶层破坏的现象，说明胶层在此模型中并没有被破坏。徐绯等[24]在蜂窝夹芯结构侧向压缩行为研究中，发现胶膜的强度、刚度改变后，不改變蜂窝夹层结构的破坏位置和破坏形式，结构承载能力的变化最大不超过5%，认为胶层参数对结构压缩载荷的承载能力影响很小。因此，选用抛弃胶层Cohesive单元建模的方法，将胶层对各组分的良好黏结作用，以各实体单元层之间的共节点方法来实现，这既实现了胶层的黏结作用，保证了泡沫夹芯结构损伤的连续性，也免去了引入胶层Cohesive单元带来的模型复杂化。

将面板和PMI芯材的单元类型设置为实体，三维8节点缩减积分单元（C3D8R）。采用这种单元时，单元形状对缩减积分单元的计算精度影响不大，在积分点上的应力结果相对准确，这对于维修区域不规则单元形状的有限元计算十分有利。完好试验件的有限元模型如图7所示。根据实际修补方式和修补参数建好的典型修补试件的有限元模型如图8所示。

复合材料层合板的强度计算常采用单纯静强度渐进损伤分析方法，但泡沫夹芯复合材料有其独特结构，若采用单纯静强度渐进损伤分析会与真实情况差距很大。为了解决这一问题，本文通过引入线性屈曲模态来考虑初始缺陷，即利用弧长法，将夹芯结构的初始缺陷考虑为线性屈曲模态，用后屈曲强度分析Riks算法的结果来代表模型的侧向压缩强度。

根据上述模型，利用ABAQUS有限元商用软件的脚本接口，编写关于面板的材料参数刚度退化脚本程序，以实现面板材料的刚度退化。用ABAQUS软件USDFLD子程序格式，将含有渐进损伤分析的Tsai-Wu失效准则用FORTRAN语言编写出来，以实现复合材料面板在Tsai-Wu失效准则下的渐进损伤过程。

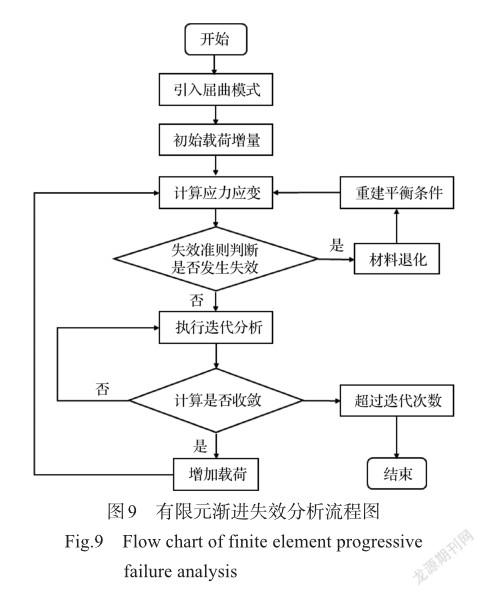
有限元渐进失效分析流程如图9所示。建立有限元模型并进行线性屈曲分析，得到泡沫夹芯结构的各阶屈曲模态，引入泡沫夹芯结构的前5阶屈曲模态作为结构的初始状态，取初始缺陷破坏因子为夹芯厚度1%，即0.065mm，采用线性逐步加载的方式对结构进行强度分析，求解每个增量步中结构的应力应变。由Tsai-Wu损伤准则判断面板材料是否失效，并对失效后单元的材料参数进行刚度退化处理，在下一增量步中对刚度退化后的结构再进行应力应变分析，并对单元的材料失效进行判断和刚度退化处理，循环往复，直至结构完全失效无法迭代计算并停止加载。

4结果分析与讨论

4.1侧向压缩强度

4.1.1考虑初始缺陷

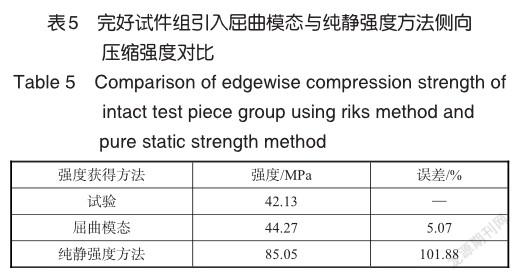
在正式开始分析前，先对比引入线性屈曲模态和不引入屈曲模态方法对强度计算的不同，并分析其与实际试验结果的吻合度。以完好试件组为例，分别利用这两种计算方法，得出计算结果和与试验时的误差见表5。可见引入线性屈曲模态的计算方法在夹芯结构的侧向压缩强度计算上与实际试验结果更加符合。

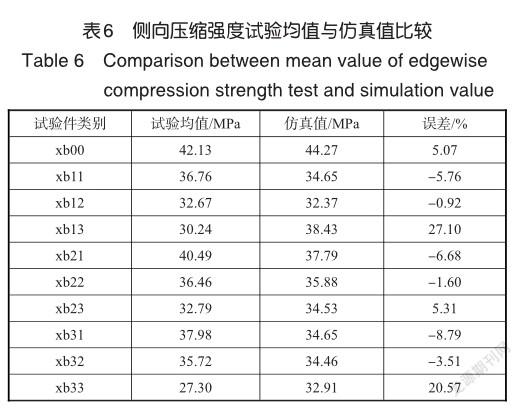
分别对试验件建立有限元模型并进行分析，将侧向压缩试验的试验结果与有限元模型的仿真结果进行对比。完好及各修补方式和修补参数下有限元模型与对应的试验件侧向压缩强度数值见表6。

从表6中可以看出，除xb13组和xb33组外，有限元仿真计算结果在各组上的计算是相当准确的，其他修补模型有限元仿真值与试验均值误差绝对值不超过9%，可见有限元仿真模型的有效性。然而xb13组，也就是双侧面板加芯材修补试验件的仿真计算结果与试验均值相差27.10%。研究认为，该组试验件有两个面板要修补，采用了二次固化的方式，且修补为手工操作，修补涉及到易碎裂的低密度PMI泡沫芯材的替换，存在较多的内部缺陷引入可能，因此导致其该组试验件均值偏低，与仿真值偏离较远。xb33组模型的仿真值与试验值相比误差较大，分析后认为附加层重叠宽度为25mm时，附加层的直径已经达到98mm，尺寸接近试件的宽度，附加层容易受到压缩夹具的影响。而在仿真计算条件下，对模型边界条件做了简化处理，不会影响附加层的受力状况，附加层直径尺寸过大也增加了引入胶结缺陷的可能性，而在仿真分析中，用共节点方法设置胶结的质量良好，不会因为胶结缺陷导致试验件侧向压缩强度降低，正是这些原因使得附加层重叠宽度为25mm试验件（xb33）侧向压缩强度与仿真值偏差较大。

从表6的数据中也可以看到，无论是仿真计算数值还是试验结果数值，均显示单侧面板修补泡沫夹芯结构的侧向压缩强度高于单侧面板加芯材修补的形式，随面板挖补倾角的比例减小，修补试验件侧向压缩强度也减小，当附加层重叠宽度过大时，修补试验件侧向压缩强度减小。

4.1.2载荷位移曲线

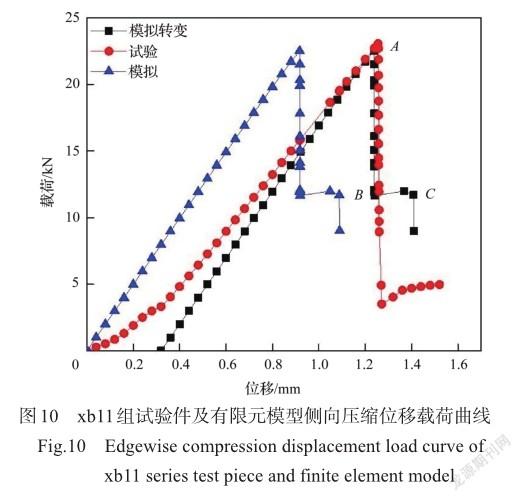
通过对试验件建立仿真模型，利用模型左侧面上参考点得到夹芯结构压缩方向位移载荷曲线。由于试验件修补前后采用的泡沫夹芯结构的材料与组成完全相同，因此修补后试验件侧向压缩过程的位移载荷曲线形式基本相同，这里取修补类xb11中的一个典型试验件与有限元模型侧向压缩位移载荷曲线进行对比，如图10所示。

有限元模型与试验件的位移载荷曲线形式基本相同，在未达到侧向压缩强度前，两者的位移与载荷基本上呈线性变化，达到侧向压缩强度后载荷值突然下降，试件失效。在位移加载初始阶段，试验件的侧向压缩载荷相比仿真模型增加较慢，这是由于试验件与夹具之间存在微小缝隙，随位移增加到0.32mm附近时，试验件与夹具间的缝隙完全消失，试验件侧向压缩载荷随位移的增加也近似呈线性，与仿真模型的载荷变化形式相同，且最终达到基本相等的侧向压缩强度。为此，将仿真的位移载荷曲线向右沿位移坐标轴平移0.32mm，如图10中所示，平移后两者在侧向压缩载荷和失效位移上数值基本相同，这验证了上文的说法。

图10中试验件侧向压缩载荷突变后稳定在5kN左右，而有限元模型侧向压缩载荷突变后稳定在10kN左右，这是因为试验中PMI泡沫在达到压缩强度后就会碎裂，几乎不再给面板提供任何支撑，而仿真模型中泡沫在达到强度极限后，会保持它达到侧向压缩强度时能提供的支撑力，这个特性是由ABAQUS中可压碎泡沫模型决定的。

4.1.3面板挖补倾角比例的影响

在上文对有限元模型验证时已经有三个不同面板挖补倾角1∶10、1∶20、1∶30，因此仅在有限元模型中增加了1∶5、1∶15、1∶22、1∶25这4种面板挖补倾角比例模型进行分析。因为1∶22这种挖补倾角比例在本次挖补修补试验中使用，故也将其纳入为有限元分析模型的一个参数值。

分析时又加入对各阶屈曲模态下侧向压缩强度的研究，因为在仿真研究中以模型各阶屈曲模态节点的位移，乘以一个为试验件厚度1/100的缺陷因子来作为模型的初始状态，通过这个初始状态来模拟试验件存在的各种微小形变和侧向压缩试验初期试验件的形变，每一阶屈曲模态的位移变形都代表了试验件可能发生的一种微小形变缺陷。通过比较同一模型各阶屈曲模态下侧向压缩强度差异，就能知道修补后的结构在稍有不同的初始状态下侧向压缩强度的变化范围，对修补后强度变化范围大小进行分析，变化范围越小，说明结构在各种微小缺陷的情况下都处于稳定的状态，修补质量较好。

不同面板挖补倾角模型各阶屈曲模态下侧向压缩强度的数据如图11所示，图中的多阶仿真组所取初始缺陷破坏因子为夹芯厚度1%，即0.065mm，因为和前三阶屈曲模态下侧向压缩强度进行对比，混合模态模型节点位移变形仅取前三阶。

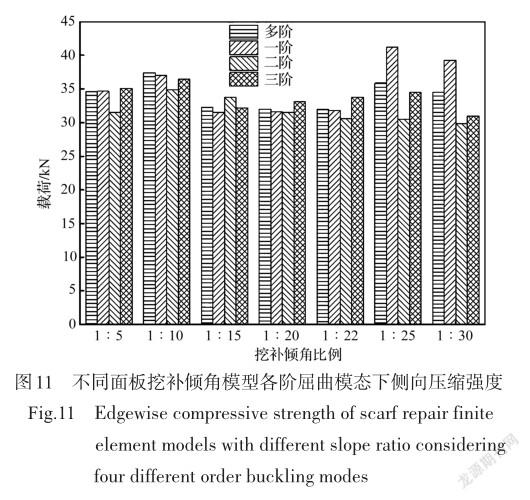
从图11中对仿真（多階）组侧向压缩强度载荷的变化看，模型侧向压缩强度随面板挖补倾角比例的减小，呈现出先增大后减小，而后再增大并最终减小的趋势。面板挖补倾角比例为1∶10的模型侧向压缩强度较大，为先出现的峰值位置，面板挖补倾角为1∶25的模型侧向压缩强度也较大，为出现的第二个峰值位置。

在图11中，从模型各阶屈曲模态下的侧向压缩强度变化范围大小来看，面板挖补倾角比例大于1：22时，模型的各阶模态下侧向压缩强度变化范围较小，修补质量较好；而面板挖补倾角比例小于1∶22，在图11中即为1∶25和1∶30时，模型的各阶模量下侧向压缩强度变化范围较大，修补后质量不佳。

综合试验结果与上述有限元仿真分析计算认为，泡沫夹芯结构在单侧面板修补时，试验件面板挖补倾角比例为1∶10～1∶22时，修补质量较好，推荐使用。在这个范围内修补后试验件侧向压缩强度随面板挖补倾角比例的减小而减小。

4.1.4附加层重叠宽度的影响

刘国春等[25]认为在修补平纹编织复合材料拉伸试件时，存在使得试验件强度取得最大值的附加层重叠宽度。Beylergil等[26]在对阶梯状接头的轴压研究中，发现随附加层重叠宽度增加，试验件破坏载荷会变大。为进一步分析附加层重叠宽度对侧向压缩强度的影响，将附加层重叠宽度修补参数的范围由原模型中的15mm、20mm、25mm这三个进行扩充，增加附加层重叠宽度参数为0mm、2.5mm、5mm、7.5mm、10mm、12.5mm、17.5mm、22.5mm的模型，对各修补模型进行侧向压缩有限元仿真，计算结果如图12所示，仿真多阶组模型的混合模态节点位移仅取前三阶。

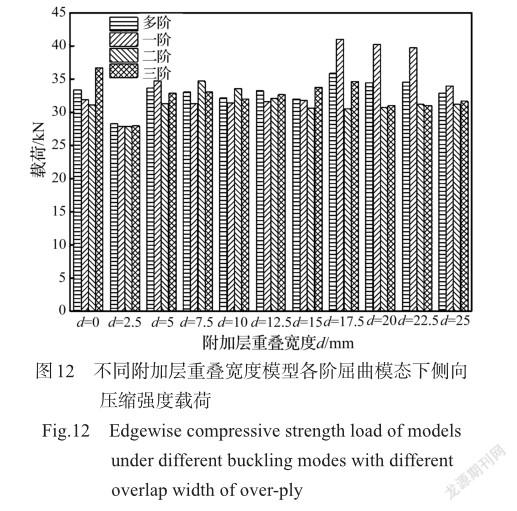
从图12中仿真（多阶）有限元模型侧向压缩强度的变化可以看出，随着附加层重叠宽度的增加，修补模型的侧向压缩强度呈现出波浪形的变化趋势，附加层重叠宽度为2.5mm处为一个波形底部，附加层重叠宽度为17.5mm处为一个波形顶部，在它们之间附加层重叠宽度为5～15mm的区域内侧向压缩强度值变化较平缓，而附加层重叠宽度为17.5mm模型的侧向压缩强度为0～25mm附加层重叠范围中出现的最大峰值。

在图12中，从模型各阶屈曲模态下的侧向压缩强度变化范围大小来看，单侧面板修补中，附加层重叠宽度为2.5～ 15mm時，各阶屈曲模态下压缩强度差异较小，修补质量较好。附加层重叠宽度为0mm在实际修补中无意义，仅作对照。附加层重叠宽度为2.5mm模型的各阶模态下侧向压缩强度变化很小，但其侧向压缩强度在所有模型中最低，不推荐采用。附加层重叠宽度为17.5～22.5mm时，模型各阶模态下的侧向压缩强度差异很大，修补质量不佳。附加层重叠宽度为25mm时，模型各阶模态下侧向压缩强度变化范围小，其侧向压缩强度同附加层重叠宽度为5～15mm时基本相同，却增加修补的材料和修补质量，这得不偿失。

综合试验结果和上述有限元仿真分析计算，认为在泡沫夹芯结构单侧面板修补时，附加层重叠宽度为5～15mm时修补质量较好，推荐使用。在附加层重叠宽度为5～ 10mm和12.5～15mm范围中，修补后试验件侧向压缩强度分别随附加层重叠宽度的增大而减小，但变化幅度不大。虽然模型附加层重叠宽度在5～15mm范围内5mm处的侧向压缩强度取得最大值，但考虑到实际修补时可能会有误差，从能够获得可靠的修补效果考虑，推荐尽可能采用附加层重叠宽度为12.5mm的修补方案。

4.2损伤模式

试验后各组面板的典型损伤形式如图13所示，试验件面板损伤处用矩形框进行示意。修补件的损伤主要在附加层区域的外围边界，如图13所示，完好试件的损伤在面板的左右两侧和中部均有出现。图13中展示了完好试件类别（xb00）中的一个损伤在中部偏左侧的试件与其他修补件进行对比，修补件的中部区域因附加层的加强作用，没有出现中部损伤的情况，这说明修补的有效性。有限元模型侧向压缩仿真模拟后的面板的损伤情况如图14所示，图中失效单元通过颜色标记高亮展示，仿真结果中面板的失效位置与试验中基本一致。

4.3失效机理分析

为了分析试验件达到侧向压缩强度时的失效原因，注意到在位移载荷曲线图10上有转折点A、B两点，A点是有限元模型发生结构失效的起点，B点是有限元模型的受力达到了新的平衡的起点，弄清楚了从A点到B点有限元模型各部分应力应变是如何变化，有哪些部分发生了损伤或损伤扩展，也就知道了泡沫夹芯结构的失效机理。

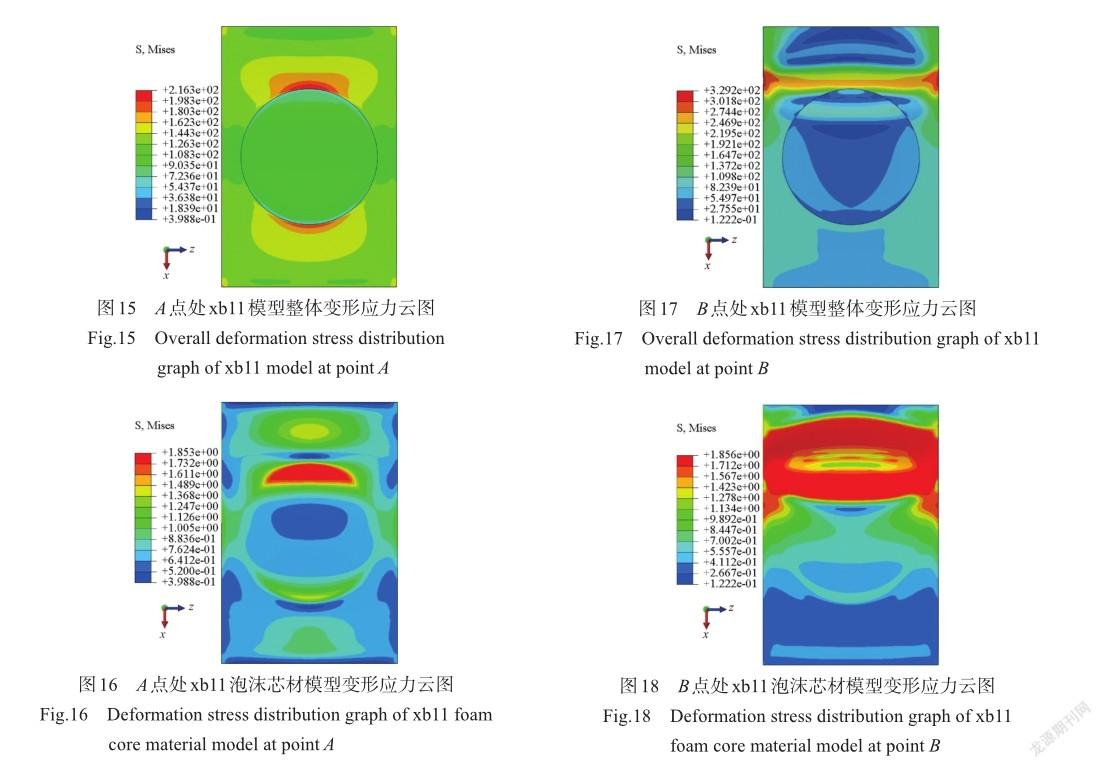
在第一个转折点A处，通过对有限元模型整体变形应力云图观察，发现此时平纹编织复合材料面板远远未达到其应力强度极限，面板未损伤，应力云图如图15所示。但通过观察PMI泡沫芯材有限元模型变形应力云图，发现芯材模型一部分的应力已经达到材料压缩强度，芯材发生了损伤，芯材模型的变形应力云图如图16所示。因此，认为泡沫夹芯结构达到其侧向压缩强度，不是由于面板的破坏，而是强度较弱芯材破坏导致的。

继续对图10曲线中转折点B处模型的变形应力状态进行研究，观察此时有限元模型的整体变形应力云图，如图17所示。从图10中知夹芯结构由A状态到B状态压缩方向位移几乎没有增加，但芯材破坏处面板的应力急剧增加，从泡沫芯材模型的变形应力云图18与图16的对比中能看出，芯材应力达到其压缩强度的部分变多，芯材损伤面积扩大，这一点则说明了面板的应力突变与芯材损伤扩展有关。PMI泡沫芯材的弹性模量与平纹编织面板相比很小，结构的承载主要靠面板材料，而从此时的图17来看，面板并未达到材料强度极限，也就是说此时面板材料并没有失效，但其承载载荷的能力却随着芯材失效面积的扩大而急剧降低，这印证了上文所说的泡沫夹芯结构达到侧向压缩强度极限是泡沫芯材的破坏导致的。

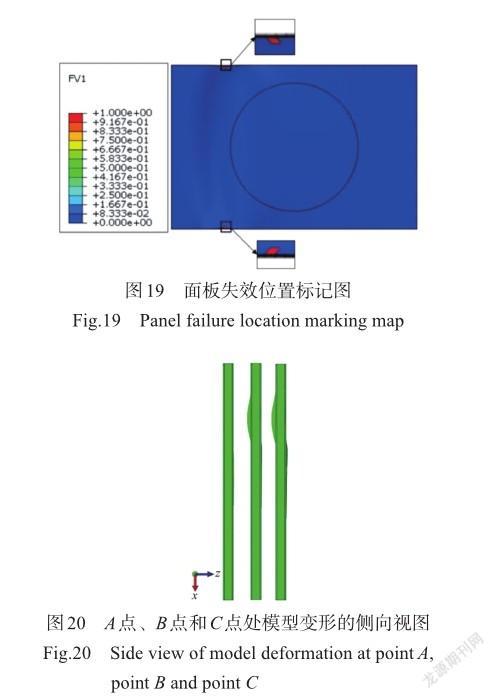
侧向压缩试验结束后，试验件面板确实出现了损伤，而在有限元模型侧向压缩过程中，直至侧向压缩载荷突降后达到B点，有限元模型再次受力平衡，模型面板也未出现损伤。推测模型面板的损伤发生在后续的侧向压缩过程，注意到图10中仿真的位移载荷曲线B点后还有一个转折点C，观察该处有限元模型面板变形应力云图情况，发现有限元模型面板确实在此时出现损伤，将损伤处面板的失效单元标记出来，并在面板上下两侧边将破坏处框选放大，如图19所示。

在侧向压缩过程的最后，面板发生了失效，根据上文知泡沫夹芯结构的侧向压缩强度的降低与芯材的损伤有关，然而芯材的损伤如何影响夹芯结构的面板，进而使整个泡沫夹芯结构的侧向承载能力下降，并最终使得面板损伤，这一点可以通过观察模型位移载荷曲线A点、B点和C点处模型变形的侧向视图来研究，有限元模型在各点处的变形侧向视图如图20所示，从左到右依次为A点、B点和C点处模型变形的侧向视图。

A点处面板未出现明显面外位移变形，但泡沫芯材开始出现损伤，B点处面板面外位移变形明显，泡沫芯材损伤面积扩大，同时从图17中可知面板应力相对于A点有了突增，C点处面板的面外位移变形加大，此时面板材料出现损伤。可以看出，芯材损伤导致面板局部无支撑，在侧向压缩载荷的作用下面板发生了局部屈曲，并使得泡沫夹芯结构失效，整个结构的侧向压缩承载能力突降，随着位移加载的继续，面板变形过大，最终发生材料的损伤。

4.4纯屈曲分析

从表7中看到试验件侧向压缩时能够承受的最大载荷值均小于仿真模型一阶屈曲载荷，这说明试验件未达到屈曲状态就已经失效，通过上文分析可知，试验件未达到屈曲状态的原因是泡沫芯材先达到了压缩强度，发生了失效。根据试验件应变计的记录结果显示，试验件在侧向压缩过程中没有发生整体屈曲破坏，但观察到了面板在芯材失效后，发生局部屈曲的试验现象。因此认为试验件失效机理为芯材失效后，面板局部无支撑，发生了局部屈曲。

表7中多数模型的一阶屈曲载荷值与试验中真实的最大侧向压缩载荷有很大差距，但也观察到xb00组和xb21组的试验承载能力与一阶屈曲载荷值比较接近，xb00组是完好试件，xb11组是修补时对母板去除最小的试件，这都说明一阶屈曲载荷对完好试验件或接近完好试验件的最大侧向压缩载荷能提供一个预测值，这个预测值稍微偏大，但误差分别仅为3.14%和6.15%，准确率很高。

通过上文分析可知，试验件到达屈曲前泡沫芯材就已经失效，而屈曲特征值分析得到的屈曲载荷值只考虑材料的弹性模量和边界条件，不考虑材料的失效，因此与试验得到的最大侧向压缩载荷存在误差。若芯材的强度变大，足以支撑试验件达到屈曲状态，用仿真模型进行一阶屈曲载荷值计算，来预测试验件的侧向压缩强度会更加准确，这一点有助于优化泡沫夹芯结构的强度设计。A.G.Mamalis等[27]也认为泡沫夹芯结构中芯材的性能和强度非常重要，是决定泡沫夹芯结构侧向压缩失效模式的重要因素。

5结论

通过对平纹编织面板泡沫夹芯结构修补试验件建立渐进损伤的有限元模型，进行侧向压缩数值仿真，与试验结果进行对比分析。

（1）从泡沫夹芯结构修补后的侧向压缩强度、失效过程、面板损伤位置、失效机理等多方面验证了模型的有效性。

（2）根据有限元仿真结合试验结果分析，认为泡沫夹芯结构的侧向压缩失效机理为芯材损伤导致面板局部无支撑，在侧向压缩载荷的作用下面板发生了局部屈曲，并使得泡沫夹芯结构失效，达到侧向压缩强度。

（3）分析面板挖补倾角比例对模型侧向压缩强度的影响，得出面板挖补倾角为1∶10到1∶22时，修补质量较好，在这个范围内修补后，试验件侧向压缩强度随面板挖补倾角比例的减小而增大。分析面板附加层重叠宽度对模型侧向压缩强度的影响，为了获得可靠的修补效果，推荐尽可能采用附加层重叠宽度为12.5mm的修补方案。

（4）通过纯屈曲分析与试验结果对比，认为对完好泡沫夹芯结构或者母板损伤小的修补件，纯屈曲分析预测其最大侧向压缩载荷准确率高。

参考文献

[1]刘国春，魏桂明，杨文锋，等.复合材料泡沫夹芯板胶结修理的压缩性能[J].宇航材料工艺， 2020， 50（2）： 16-21. LiuGuochun，WeiGuiming，YangWenfeng，etal. Compression performance of adhesively repaired foam core sandwich composite[J]. Aerospace Materials & Technology， 2020， 50（2）： 16-21. （in Chinese）

[2]周春苹，刘武帅，王轩，等.含表面划伤平纹编织面板蜂窝夹芯结构侧向压缩渐进失效分析[J].玻璃钢/复合材料， 2019（7）： 5-10. Zhou Chunping， Liu Wushuai， Wang Xuan， et al. Study on edgewise compression performance of honeycomb sandwich structure with scratch damage[J]. Fiber Reinforced Plastics/ Composites， 2019（7）： 5-10. （in Chinese）

[3]张铁纯，张世秋，王轩，等.挖补修理复合材料夹芯结构侧向压缩性能研究[J].航空科学技术，2021，32（8）：1-11. Zhang Tiechun， Zhang Shiqiu， Wang Xuan， et al. Research on lateral compression performance of scarf repaired composite sandwich structure[J]. Aeronautical Science & Technology， 2021，32（8）：1-11. （in Chinese）

[4]李劍峰，燕瑛，廖宝华，等.复合材料蜂窝夹芯结构单面贴补弯曲性能的分析模型与试验研究[J].航空学报， 2013， 34（8）： 1884-1891. Li Jianfeng， Yan Ying， Liao Baohua， et al. Analysis model and experimentalstudyofbendingbehaviorofcomposite honeycomb sandwich structures with one side bonded repair[J]. Acta Aeronautica et Astronautica Sinica， 2013， 34（8）： 1884-1891. （in Chinese）

[5]Zhang T，Yan Y，Jin C. Experimental and uumerical investigations of honeycomb sandwich composite panels with open-hole damage and scarf repair subjected to compressive loads[J]. The Journal ofAdhesion，2016，92（5）：380-401.

[6]王跃全，童明波，朱书华.复合材料层合板胶结贴补修理渐进损伤分析[J].复合材料学报， 2011， 3（28）： 197-202. Wang Yuequan， Tong Mingbo， Zhu Shuhua. Progressive damage analysis on adhesively bonding patch repair of composite laminates[J]. Acta Materiae Compositae Sinica， 2011， 3（28）： 197-202. （in Chinese）

[7]Campilho R D S G，De Moura M F S F，Ramantani D A，et al. Buckling behaviour of carbon epoxy adhesively-bonded scarf repairs[J]. Journal of Adhesion Science and Technology，2009，23（10-11）：1493-1513.

[8]邓健，周光明，尹乔之，等.双面贴补层合板压缩屈曲渐进损伤分析[J].航空学报， 2016， 37（5）： 1526-1535. Deng Jian， Zhou Guangming， Yin Qiaozhi， et al. Progressive damage analysis of double strap bonding repaired laminates underbucklingcompression[J].ActaAeronauticaet Astronautica Sinica， 2016， 37（5）： 1526-1535. （in Chinese）

[9]白瑞祥，王秀秀，王蔓.碳纤维复合材料修补结构的ANSYS参数化建模技术与修补参数讨论[C]//第19届全国结构工程学術会议.济南，2010：321-324. Bai Ruixiang， Wang Xiuxiu， Wang Man. ANSYS parametric modeling technology and repair parameters discussion of carbon fiber composite repair structure[C]//The 19th National Academic Conference on Structural Engineering. Jinan， 2010： 321-324. （in Chinese）

[10]程起有，童小燕，姚磊江，等.基于神经网络的复合材料胶结修补参数优化[J].计算机仿真， 2008， 25（12）： 205-207. Cheng Qiyou， Tong Xiaoyan， Yao Leijiang， et al. Parameter optimization for bonding repair of composite laminates based on neural network[J]. Computer Simulation， 2008， 25（12）： 205-207. （in Chinese）

[11]吕胜利，程起有，姚磊江，等.损伤复合材料层板胶结修理的优化设计[J].机械强度， 2007（4）： 598-600. Lyu Shengli， Cheng Qiyou， Yao Leijiang， et al. Optimization design of adhesive bonding repair of damaged composite laminates[J]. Journal of Mechanical Strength， 2007（4）： 598-600. （in Chinese）

[12]王宝芹，王沫楠，刘长喜.基于多尺度方法的蜂窝夹层复合材料结构轴向压缩稳定性[J].复合材料学报， 2020， 37（3）： 601-608. Wang Baoqin， Wang Monan， Liu Changxi. Stability of honeycombsandwichcompositestructureunderanxial compression based on multi-scale method[J]. Acta Materiae Compositae Sinica， 2020， 37（3）： 601-608.（in Chinese）

[13]刘智良，程小全，胡仁伟，等.含不同形状分层缺陷蜂窝夹层板的压缩性能[J].复合材料学报， 2009， 26（5）： 153-158. Liu Zhiliang， Cheng Xiaoquan， Hu Renwei， et al. Compression properties of honeycomb sandwich plates with different shape delamination defects[J]. Acta Materiae Compositae Sinica， 2009， 26（5）： 153-158. （in Chinese）

[14]万玉敏，张发，刘长喜，等.飞机典型薄壁复合材料夹层结构整体屈曲[J].复合材料学报， 2018， 35（8）： 2235-2245. Wan Yumin， Zhang Fa， Liu Changxi， et al. Overall buckling of typical thin-wall sandwich composites applied on the aircraft[J]. Acta Materiae Compositae Sinica， 2018， 35（8）： 2235-2245.（in Chinese）

[15]陈悦，朱锡，李华东，等.复合材料夹芯梁屈曲破坏模式及极限承载[J].复合材料学报， 2016， 33（5）： 991-997. Chen Yue， Zhu Xi， Li Huadong， et al. Buckling failure mode and ultimate load of composite sandwich beam[J]. Acta Materiae Compositae Sinica， 2016， 33（5）： 991-997.（in Chinese）

[16]Fagerberg L，Zenkert D. Imperfection-induced wrinkling material failure in sandwich panels[J]. Journal of Sandwich Structures & Materials，2016，7（3）：195-219.

[17]曹景斌，王松，章强.树脂基复合材料湿热压缩性能研究[J].航空科学技术，2020，31（3）：47-52. Cao Jingbin， Wang Song， Zhang Qiang. Research on resin composite hydrothermal compressive properties[J]. Aeronautical Science & Technology， 2020， 31（3）：47-52. （in Chinese）

[18]林国伟，李新祥.复合材料壁板后屈曲分析失效准则的适用性研究[J].机械强度， 2020， 42（3）： 565-572. Lin Guowei， Li Xinxiang. Applicability investigation of failure criterion for post-bucking analysis of stiffened composite panels[J]. Journal of Mechanical Strength， 2020， 42（3）： 565-572. （in Chinese）

[19]Tsai S W，Wu E M. A general theory of strength for anisotropic materials[J]. Journal of Composite Materials，1971，5（1）：58-80.

[20]孔祥宏，王志瑾.基于Abaqus的有限元渐进损伤强度分析[J].计算机应用与软件， 2012， 29（10）： 236-240. Kong Xianghong， Wang Zhijin. Finite element incremental damage strength analysis based on Abaqus[J]. Computer Applications and Software， 2012， 29（10）： 236-240. （in Chinese）

[21]Wang J，Chen B，Wang H，et al. Experimental study on the compression-after-impact behavior of foam-core sandwich panels[J]. Journal of Sandwich Structures & Materials，2015，17（4）：446-465.

[22]谭年富.复合材料泡沫夹层结构低速冲击后的面内力学性能研究[D].上海：上海交通大学， 2012. TanNianfu.Mechanicalpropertiesoffoamsandwich composites with low-velocity impact damage[D]. Shanghai： Shanghai Jiao Tong University， 2012. （in Chinese）

[23]张铁纯，张世秋，王轩，等.平纹编织面板泡沫夹芯结构修补后侧向压缩性能[J].复合材料科学与工程，2021（3）：51-59. Zhang Tiechun， Zhang Shiqiu， Wang Xuan， et al. Research on edgewise compression properties of plain weave panel foam sandwich composite material after repair[J]. Composites Science and Engineering ，2021（3）：51-59. （in Chinese）

[24]徐緋，刘亚各，闫慧敏.蜂窝夹芯结构冲击损伤后的压缩行为研究[J].应用力学学报， 2013， 30（5）： 726-730. Xu Fei， Liu Yage， Yan Huimin. Honeycomb sandwich compositestructurewithpre-damageunderuniaxial compression[J]. Chinese Journal of Applied Mechanics， 2013， 30（5）： 726-730. （in Chinese）

[25]刘国春，秦文峰，杨文锋，等.平纹编织复合材料挖补修理附加层优化研究[J].合肥工业大学学报（自然科学版）， 2015， 38（8）： 1045-1048. Liu Guochun， Qin Wenfeng， Yang Wenfeng， et al. Parameters optimization of covering layer of plain-woven composite laminates with flush repair[J]. Journal of Hefei University of Technology， 2015， 38（8）： 1045-1048. （in Chinese）

[26]BeylergilB，AktasA，CunediogluY.Bucklingand compressive failure of stepped-lap joints repaired with composite patches[J]. Journal of Composite Materials，2012，46（26）：3213-3230.

[27]Mamalis A G，Manolakos D E，Ioannidis M B，et al. On the crushing response of composite sandwich panels subjected to edgewise compression：experimental[J]. Composite Structures，2005，71（2）：246-257.

Progressive Failure Analysis of Repaired Foam Sandwich Structure with Plain Weave Faceplate Under Edgewise Compression

Wang Xuan，Gang Qingyong，Zhang Shiqiu

Civil Aviation University of China，Tianjin 300300，China

Abstract： In order to study the influence of the scarf repair on the edgewise compression performance of the foam sandwich structure with plain weave faceplate， by the use of USDFLD material subroutine， Tsai-Wu criterion was set up for material failure of the faceplates. The linear buckling mode is considered as the initial defect， and the progressive failure analysis model for the repaired foam sandwich structure with plain woven faceplates is established. The analysis results show that the validity of the model is verified by experiments. The repair quality of the sandwich structure is better when the slope ratio of scarf repair is 1：10 to 1：22， and the edgewise compression strength increases with the decrease of the slope ratio of scarf repair. When the overlap width of the additional layer is in the range of 5mm to 15mm， the repair quality is better. The edgewise compression strength decreases with the increase of the overlap width of the additional layer， but the change range is not great. The analytical methodology involving the pure buckling analysis is more accurate to predict the maximum edgewise compression load for the intact test pieces and the repaired test pieces with little damage. The failure mechanism of the sandwich structure under edgewise compression is that after the failure of the core material， the faceplate buckles locally， and then the faceplate fails when the test piece reaches its edgewise compression strength.

Key Words： plain weave； composite； repair； foam sandwich； edgewise compression； progressive failure analysis