基于改进贪心算法的无人机集群协同任务分配

陈宇恒 陈进朝 陈雪聪

摘要：无人机集群由于其强大的信息共享与行为协作等优势，在军事、民用及科研等领域发挥了重要作用。然而无人机集群在执行大规模任务时，任务的时间约束、时序关系以及性能要求都对集群任务的协同规划与分配提出了巨大的挑战。针对多无人机协同飞行约束下的任务分配问题，本文提出了一种基于改进贪心算法的无人机集群协同任务分配算法，在保证无人机间协同飞行以及任务间时序约束的前提下，优化无人机集群的飞行时间与距离。该算法借鉴图论中的有向图来表示任务间协同飞行约束关系，并依据改进的贪心算法对任务进行局部最优分配、优化，有效获得时间最优、距离最优两种策略下的近似最佳飞行路径。在构建的覆盖扫描任务场景上进行试验对比，验证了本文所提算法的有效性，该算法相较于传统解决方法在时间与距离性能上最高能提升20%。

关键词：无人机集群；任务分配；协同任务；图论；改进贪心算法

中图分类号：V355文献标识码：ADOI：10.19452/j.issn1007-5453.2022.04.003

基金項目：国家自然科学基金（62106202）；航空科学基金（2020Z023053004）

无人机具有灵活性高、无人驾驶、自主控制、可操作性强等优点，在区域侦察、快递投送及农业喷洒等众多领域优势明显，其军用民用的价值愈发突出，应用也越加广泛[1]。但是，当使用无人机集群执行大规模任务时，任务中的子任务对无人机的要求以及无人机之间的性能也各不相同，任务的规划分配存在挑战[2]。学者们在无人机任务分配领域做了大量的研究，包括多架同构或异构无人机的任务分配。从算法的角度来看，任务分配问题是一个NP-hard问题。对于需要大量无人机参与的任务规划，由于环境和无人机的各种限制，往往将任务规划通过层次控制的方式划分为若干层次[3]，将问题简化为组合优化问题，从而提高可行性和规划模块的可扩展性。目前，任务分配的顶层规划分为集中式和分布式。

基于集中规划的算法可以分为以下几类：（1）优化算法包括动态规划算法[4]、分支定界算法[5]等；（2）启发式随机搜索算法不需要遍历整个解空间来寻找最优解，通常得到次优解，遗传算法[6]、粒子群优化算法[7]和模拟退火算法[8]都属于启发式算法；（3）其他相关的算法，如S. Rathinam的常数因子逼近法[9]等。常见的确定性图搜索算法，如A*算法[10-11]、Dijkstra算法、BellmanFord算法、广度优先搜索算法。

与集中式任务规划相比，分布式规划在通信带宽要求、环境变化等方面更具优势，因此分布式规划策略具有更广泛的应用。关于分布式混合整数线性规划框架下的任务规划有很多研究，该框架对任务规划问题描述具有较强的适应性。M. B. Dias等[12]提出的基于拍卖机制的规划策略被广泛应用于任务规划。

尽管学者们提出了许多解决任务分配的相关算法，但在多无人机协同飞行执行集群任务的分配问题并没有得到很好的解决[13]。本文采用图论表述任务中子任务之间的协同飞行关系，依据改进贪心算法提出了基于改进贪心算法的多无人机协同任务分配算法（MAA）。该算法结合改进贪心算法，根据最短时间或最短路径的要求对任务进行分配，实现了多无人机集群协同飞行约束下的任务分配。MAA仅适用于具有时间序列协同飞行约束的任务分配。

1系统模型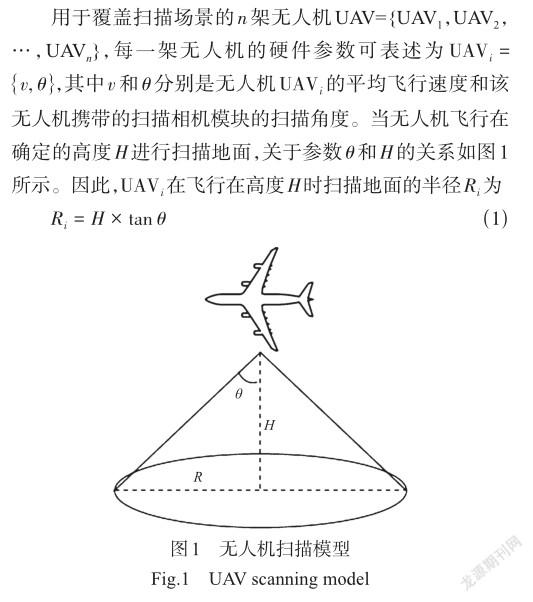

1.2任务模型

任务可以根据任务描述划分为多个子任务，用于执行任务的无人机集群由能力不同的无人机组成，子任务可以由一架或多架无人机执行。任务可以分为两大类：所有无人机都需要执行的全局任务和根据任务需求确定无人机的数量去执行的局部任务。子任务模型如图2所示。两类任务又可以分为以下4个子类：

（1）全局点任务：所有无人机都需要执行只包含一个坐标点的任务。

（2）局部点任务：只能分配给一架无人机，并且只包含一个坐标点。任务信息包括子任务点的坐标以及无人机在该点需要执行的操作。

（3）局部线任务：只能分配给一架无人机，由多个坐标点组成。每个点的执行顺序已经由任务需求确定。任务信息包括每个点的坐标以及无人机在每个点需要执行的操作。

（4）局部区域任务：由一架或多架无人机执行。任务信息包括构成该区域的坐标集和无人机在该区域内需要执行的操作。

1.3时序协同约束

1.3.1协同约束定义

2基于改进贪心算法的多无人机协同任务分配

多无人机的协同任务分配需要保证子任务在宏执行顺序上和任务要求的时序上保持一致，因此将协同任务分配分为三个阶段。子任务分配次序确定遍历子任务的次序，确保子任务的执行次序能够符合时序要求；无人机的选择阶段是根据子任务的类型及规划策略将子任务分配到无人机；最后，根据时序约束对任务队列中子任务的次序调换，实现相应策略下的任务队列优化。

2.1确定子任务分配次序

依靠无人机之间的通信机制可以实现无人机子任务执行状态的发布，因此只需要保证子任务的遍历分配顺序和任务要求的时序顺序保持一致，那么无人机在执行子任务时通过向需要协同飞行的无人机通信发布自己的任务执行状态来控制子任务的执行顺序，保证子任务宏执行次序的准确性，从而实现集群任务的时序约束规划过程。

根据子任务之间时序约束以及保存时序约束有向图的特点，图论中的广度优先遍历搜索方法能够很好地满足子任务访问次序要求。采用广度优先遍历方法遍历任务的时序约束关系图，针对每一子任务，选择在相应策略下最合适的无人机来执行子任务。

2.2无人机的选择

3试验及结果

为了简化模型，假设无人机的飞行高度保持在一定高度不变。根据图1所示模型可知，飞行高度决定了无人机的扫描半径，那么无人机的扫描半径也保持不变。使用表1的无人机进行任务分配，通过与基于贪心算法的多无人机协同任务分配算法（CMAG）、短距离优先算法（SDF）和短时间优先（STF）算法以及遗传算法（GA），评估MAA算法。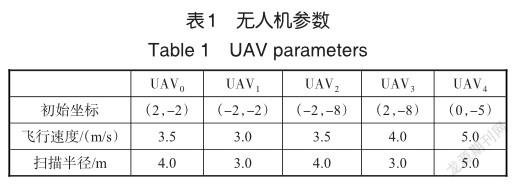

图4、图5展示了由三种任务类型子任务组成的复合任务以及由单一类型子任务组成的任务使用不同算法的结果。从图中可以看到，短距离优先算法和短时间优先算法由于不需要考虑时序协同约束关系，其分配结果相较于另外三种算法都有更好的性能。

在两种分配策略下，对多类型子任务组成的任务进行分配的结果，MAA的算法都优于GA算法且接近SDF或者STF，说明MAA取得的局部最优结果接近最优解。在对单一类型子任务组成的任务分配时，相比较于MAA通过局部的优化，GA算法通过交叉变异过程能够从更大的范围找到更好的解，但其所获取的解不能保证时序约束的准确性。

与CMAG算法相比，由于在子任务分配和无人机选择两个阶段后进行了一定的任务队列优化，在复合类型或单一类型任务中的某些情况下任务分配效果都有一定的提升，最高提升达20%。

4結束语

本文提出一种基于改进贪心算法的异构多无人机集群协同飞行任务分配算法。将任务分配与图论中的广度优先遍历方法相结合，采用改进贪心算法优化任务分配过程，解决了将有时序约束的任务分配到无人机集群的任务分配问题。试验结果表明，与传统的遗传算法等相比，MAA在解决多类型任务的任务分配问题上更接近最优解。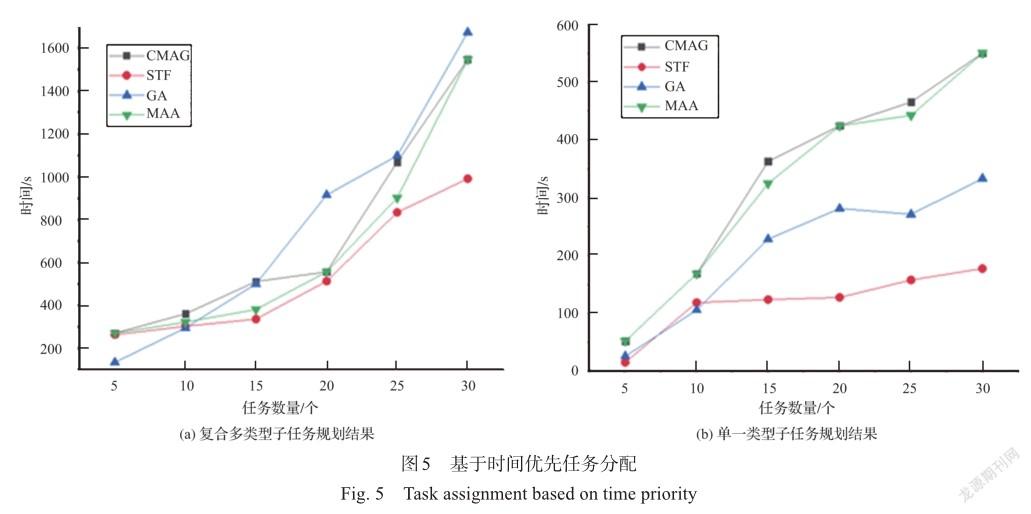

参考文献

[1]孙小雷，齐乃明，董程，等.无人机任务分配与航迹规划协同控制方法[J].系统工程与电子技术，2015，37（12）：2772-2776. Sun Xiaolei， Qi Naiming， Dong Cheng， et al. Cooperative control method of UAV task allocation and track planning[J]. Systems Engineering and Electronic Technology， 2015，37 （12）： 2772-2776. （in Chinese）

[2]李华伟.多无人机协同任务规划研究与实现[D].西安：西安电子科技大学，2014. Li Huawei. Research and implementation of multi UAV cooperative mission planning[D]. Xian：Xian University of Electronic Science and Technology， 2014. （in Chinese）

[3]Pachter M，Chandler P R. Challenges of autonomous control[J]. IEEE Control Systems Magazine，1998，18（4）：92-97.

[4]Sakoe H，Chiba S. Dynamic programming algorithm optimization for spoken word recognition[J]. IEEE Transactions on Acoustics，Speech，and Signal Processing，1978，26（1）： 43-49.

[5]Ross G T，Soland R M. A branch and bound algorithm for the generalized assignment problem[J]. Mathematical Programming，1975，8（1）：91-103.

[6]Ye F，Chen J，Tian Y，et al. Cooperative task assignment of a heterogeneous multi-UAV system using an adaptive genetic algorithm[J]. Electronics，2020，9（4）：687.

[7]Li M，Liu C，Li K，et al. Multi-task allocation with an optimized quantum particle swarm method[J]. Applied Soft Computing，2020，96：106603.