面向上市企业财务报表舞弊判断的机器学习算法研究

章银平，郭凤华

（1.安徽财贸职业学院，安徽 合肥 230601；2.安徽财经大学 会计学院，安徽 蚌埠 233030）

上市公司所披露的财务报表对使用者的决策起到很大影响，随着科技发展和社会进步，财务舞弊手段也更加高明，依靠传统财务报告分析手段完全判断财务舞弊很有难度［1］。舞弊行为不断披露会使得投资者丧失对于企业的信心，继而从根本上动摇资本市场的信用根基，阻碍其发展［2］。目前常用于财务舞弊识别的机器算法主要基于分类技术，主要有K 邻近（KNN）、人工神经网络（ANN）、支持向量机（SVM）、Logistic 回归和随机森林（RF）等［3］。目前的众多研究集中于以单个分类模型对财务报告舞弊行为进行识别，关于以集成学习算法构建财务报表舞弊识别模型的研究较少［4］。因此研究提出建立基于集成机器学习算法的财务报表舞弊判断模型，并引入机器学习算法中的SVM 模型以及KNN 模型作为对照组。

1 基于随机森林算法的企业财务报表舞弊判断

1.1 基于随机森林算法的财务舞弊判断模型构建

上市企业财务报表舞弊是当前市场监管的重点内容，但是传统的舞弊监管手段非常耗时耗力，因此利用新兴技术就成为解决这个问题的主要途径［5］。在目前的新兴技术中，计算机智能算法是应用非常广泛的一种技术，对于财务报表这种纯粹的数据信息，计算机智能算法非常擅长相关的处理工作。在目前的智能算法中，随机森林算法在样本大、数据异常时，依然能够保持较高准确性、精度和较快运算速度［6］。因此，研究在构建上市企业财务报表舞弊判断模型时，选择随机森林算法作为模型的核心技术。基于此，本次研究选择基于机器学习算法中的随机森林算法来进行企业财务报表舞弊判断模型的构建［9］。

随机算法作为一种集成算法，以决策树为基本单元，通过集成学习的方法完成决策树的集成。N棵树得到N个分类结果，汇总输出投票次数最多的一项［7-8］。在随即将森林算法进行运算的过程中，其决策规则描述为：首先采用bootstrap 方法抽样N个子样本，形成新的训练集，作为分类数，重复M次，得到M棵分类树；将输入传递到随机森林中，由决策树完成接收，每棵树预测的分类设定为独立的，并以此为标准进行投票，作为最终分类结果的判据。将M棵树的分类结果进行集合，通过多数投票的方式得到最终的分类结果［10-11］。根据以上步骤，随机森林的决策规则如下图1 所示。

图1 随机森林决策规则

则在一个训练集(x,y) 中，随机森林分类模型结果用下式表示：

在式（1）中，fi(x)表示单个决策树分类结果；y表示输出变量，其取值范围［-1，1］，取值为-1 表示其属于舞弊组，否则属于正常组；i表示决策树数量，研究取i=100；I(x)表示示性函数。得到一组分类模型h1(x),h2(x),...,hi(x)后，则用于表示样本分类正确与错误分类的平均票数之差的余量函数可表达为下式：

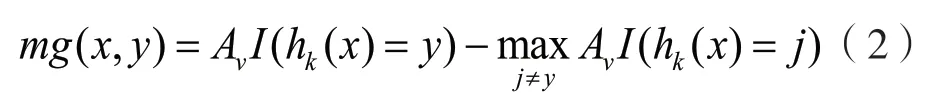
在式（2）中，Av(x)表示取平均数。余量函数越大则分类预测效果越好、结果越可靠［12-14］。随着决策树增加，分类模型hi(x)服从于强大数定律，此时泛化误差将趋于上限值，避免算法过度拟合。其中，生成决策树进行特征选择时，研究选用的最优特征选择方式是基尼指数最小化准则。对于上述样本，基尼指数表示为：

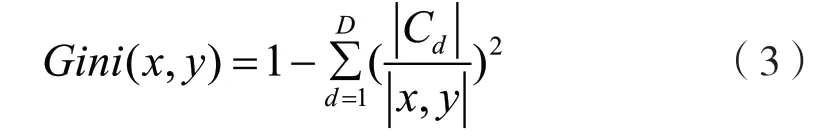
在式（3）中，C d是样本中属于第d类的样本子集，D是类的个数。

1.2 算法数据预处理与舞弊评估设计

现有的上市公司财务舞弊一般情况都为虚假披露盈利，但不同舞弊行为所反应在财务报告上的数据也是不尽相同的［15］。因此研究通过对现有舞弊手段的分析，找出每种手段影响力较大的财务指标，基于此构建指标体系，从而建立判断模型。构建的财务指标体系如图2 所示。

图2 财务舞弊判断模型店财务指标体系示意图

如图2 所示，指标体系分为规模指标、流动性指标、营运指标、盈利指标、每股能力指标、增长指标这六大类。其中规模指标中的二级指标包括资产总计、所有者权益合计、固定资产合计、少数股东权益、营业总收入、营业外收入、营业收入以及少数股东损益；流动性指标包括负债合计、货币资金、短期借款、长期借款、流动负债合计、流动资产合计、流动比率和速动比率；营运指标下的二级财务指标最多，包括应收款账、其他应收款、应付票据、存货、预付款项、预收款项、存货净额、累计折旧、营业总成本、存货周转率、应收款项周转率、流动资产周转率、固定资产周转率、股东权益周转率、总资产周转率和总资产周转天数；盈利指标下的二级指标包括营业利润、归属于上市公司的净利润、利润总额、净利润、资产减值损失、主营利润、投资收益、销售毛利率、销售净利率、营业利润率、无形资产摊销和长期待摊费用摊销；每股能力指标下的二级财务指标有基本每股收益、稀释每股收益、每股收益摊薄和每股净资产；增长指标包括基本每股收益同比增长、营业收入同比增长、营业利润同比增长、利润总额同比增长、净利润同比增长、净资产同比增长、总资产同比增长、营业利润同比增长、净利润增长率、总资产增长率和每股收益增长率这些二级指标。为保证财务指标的全面性，其来源不仅有主要财务指标，还从上市公司财务报表中覆盖了利润表、现金流量表和资产负债表。

作为典型的二分类问题，本次研究选取准确率（accuracy）、精确度（precision）、召回率（recall）、AUC 以及综合计算得出的F 得分（F-score）等指标来衡量模型效果。测试集样本根据真实类别以及预测类别的情况可以划分为真阳（True Positive）、假阳（False Positive）、真阴（True Negative）以及假阴（False Negative）四种情况；在真实类别中，将1记为True，0 记为False；在预测类别中，将1 记为Positive，0 记为Negative。以此为基础建立混淆矩阵：当真实类别与预测类别都为1 时，记为TP，即真阳；当真实类别取0，预测类别取1 时，记为FP，即假阳；当真实类别取1，预测类别取0 时，记为FN，即假阴；当真实类别与预测类别都为0时，记为TN，即真阴。则用混淆矩阵分别表示常用指标如下：

准确率即分类正确的样本在总样本之中的占比，表示如下：

精确率指TP样本在预测为真样本中的占比，表示如下：

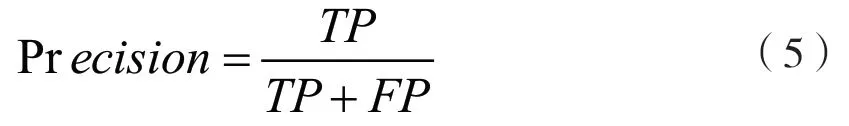
召回率指TP样本在实际为真样本中的占比，表示如下：

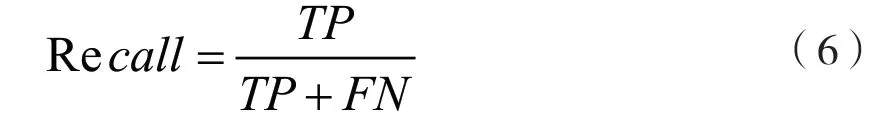
F 得分表示如下：

其中，α表示召回率的权重相对于精准率的倍数，通常取1。

研究继而引入三个指标，真阳率（True Positive Rate）又称敏感度，假阳率（False Positive Rate）表示预测为真而实际为假的样本在所有实际为假的样本中的占比，真阴率（True Negative Rate）即特异度，指预测为假并且实际为假的样本在所有实际为假的样本中的占比。以假阳率为横轴，以真阳率为纵轴，就可以得到反馈模型效果的ROC 曲线。而在ROC 曲线中，曲线下方的面积定义为AUC（Area Under the Curve），则判断模型的方法有两种，其一，曲线越靠近左上角，表示真阳率越高、假阳率越低，则模型所显示出的效果越好；其二，AUC 越大，模型效果越好。真阳率、真阴率以及假阳率分别用混淆矩阵表示如下。

真阳率的表达式如下：

真阴率的表达式如下：

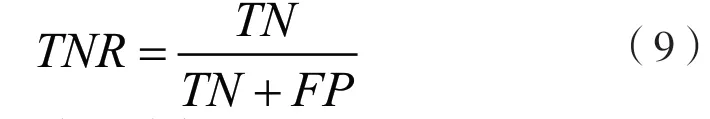
假阳率的表达式如下：

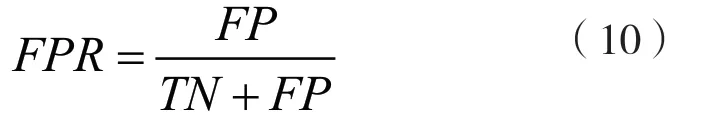
2 模型判断效果对比与实际应用分析

为探索所建立的机器学习算法模型应用于财务舞弊判断的效果，训练和测试样本选用2010—2019 年A 股上市公司年度财务报表所公布的样本作为训练集，将2020 年样本作为测试集，利用所构建的机器算法模型对上市公司财务舞弊概率进行判断分析。研究进行了1000次重复建模，将这些模型分别用于对测试样本的预测，并取其平均值。得到的三种模型的效果计算如表1 所示。

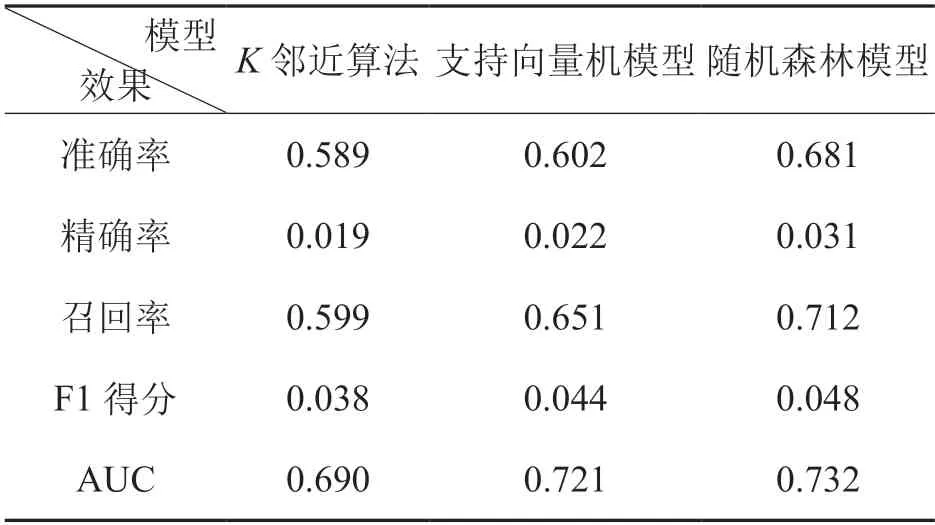
表1 三种模型效果（阈值取值0.5）

从上表可以看出准确率、精确率、召回率、F1得分以及AUC 值这5 个指标的大小排序都为随机森林模型＞支持向量机模型＞K 邻近算法，支持向量机的召回率在三个模型中是最高的，说明其对于舞弊样本的识别能力最好，而三者中对非舞弊样本识别能力最好的是随机森林模型，K 邻近算法对两类样本的识别能力相对比较接近。综上，支持向量机模型和随机森林模型的效果较K邻近算法来说更优。图3 绘出了不同阈值下三种模型的准确率、精确率、召回率和F1 得分曲线。

图3 不同阈值下三种模型的准确率、精确率、召回率和F1 得分曲线

从图3（a）中可以看出，准确率方面，三种模型的准确率都与阈值成正比，当阈值取值范围为［0，0.5］时，KNN 算法模型的准确率高于SVM模型和RF 模型；而随着阈值的增大，RF 模型的准确率在三者中达到最高；当阈值等于0.5 时，三种模型的准确率都高于50%。RF 模型在阈值取值范围为［0，0.2］时，几乎将所有样本错误分类，而在阈值取值范围为［0.7，1］时，将所有样本正确分类。图3（b）显示查全率方面，三种模型的精确率都与阈值成正比，当阈值较小时，RF模型的精确率最高，KNN 算法模型和SVM 模型的查全率随阈值的变化相对平缓；并且，RF 模型的准确率随阈值的变化较为剧烈，且仅在阈值取值范围为［0.3，0.8］时变化。从图3（c）、3（d）可以看出，在阈值取值［0，0.5］时，三种模型的召回率和F1 得分差异不大。RF 模型的召回率和F1 得分在阈值取值为［0.6，0.8］时变化剧烈，其召回率在［0.7，0.8］达到最大值，F1 得分在［0.6，0.7］达到最大值，且明显高于此时的SVM 模型和KNN 算法模型。

随机森林算法模型显示，判断概率在［0.1596，0.1967］之间的公司可以获得大于正盘的股票收益。为进一步验证模型的效果，研究进一步选择部分公司进行时间跨度为一年的股票组合回测，通过对其收益的比较来分析模型效果，如图4 所示。

图4 随机森林模型下舞弊概率最小的公司股票组合一年回测收益率

从图中可以看出，随机森林算法模型所选出的舞弊概率最小的股票组合年化收益为1.59%，远高于概率最大公司21.19%的年化损益，且高于基准收益。同时随机森林模型预测股票走势图与真实走势图十份相近，说明用随机森林算法模型选出的舞弊概率小的股票组合投资收益高、风险小，且该算法模型具有有效性和真实性。

3 结论

研究建立基于随机森林算法的财务报表舞弊判断模型，并对其效果进行评估。结果表明RF模型准确率、精确率、召回率、F1 得分和AUC 值都高于对照组两种算法，达到了0.681、0.031、0.712、0.048 和0.732；在阈值取值范围为［0.7，1］时，RF 模型将所有样本正确分类；当阈值较小时，RF 模型的精确率最高；RF 模型的召回率和F1 得分在阈值取值［0.7，0.8］达到最大值，F1 得分在［0.6，0.7］达到最大值，且明显高于此时的SVM 模型和KNN 算法模型。以上研究说明所建立的基于随机随机森林算法的财务报表舞弊判断模型可用于财务舞弊的判断，证明了机器学习算法在财务舞弊判断研究领域的有效性和准确性。