斜照明式彩色共聚焦测量系统设计及其实验研究
2022-05-28张雅丽尚文键
张雅丽,余 卿,尚文键,王 翀,刘 婷,王 寅,程 方
(华侨大学 机电及自动化学院,福建 厦门 361021)
1 引言
光学检测技术作为测量领域的常用方法之一,主要有白光干涉法[1-2]、激光三角法[3-4]、光栅投影法[5-6]和激光共聚焦法[7-8]等。随着科技的发展,在激光共聚焦技术的基础上,彩色共聚焦技术脱颖而出。彩色共聚焦技术避免了轴向机械扫描带来的耗时和机械运动误差,具有测量速度快、精度高、分辨率高等优点,可用于三维形貌重构[9-10]、粗糙度[11-12]、位移和厚度测量[13-14]等。
近年来,大量学者在彩色共聚焦相关研究领域取得显著成果。在硬件结构方面,2020 年,余卿等人[15-16]在单点彩色共聚焦的基础上,利用光纤束和数字微镜器件(Digital Micromirror Device,DMD)作为光分束器件,分别通过线扫描和一次拍照的方式实现并行测量,大大提高了测量效率。2021 年,张子龙等人[17]提出了两种基于双透镜的CCS 色散物镜初始结构,分别适用于大色散范围和高NA 色散物镜的设计。在算法研究方面,2019 年,卢文龙等人[18]提出了一种混合径向基函数网络方法来表征位移响应。2020 年,LU J F 等人[19]提出了一种自适应模态分解方法,用于色差共焦测厚中超薄材料的多峰提取。2020年,Ryo Sato 等人[20]提出一种跟踪交会法用于基于光纤的双探测器差动共焦探头。
以上关于彩色共聚焦的测量装置均为同轴照明光路,即利用分光镜等光学分光元件,将照明整合到光学系统中,照明光轴和成像光轴均垂直于被测试样。然而,这种光路结构存在一定的局限性,当被测物为高透射材料时,材料不同层的反射信号会产生混叠,系统的信噪比较低,信号串扰大,无法精确获取不同表面的光学信息;同时,由于分光镜的存在,系统的光能利用率仅有复色光源光能的1/4。针对上述问题,斜照明结构系统优势就凸显出来了。2020 年,G.Berkovic 等人[21]设计并改进了一种倾斜入射彩色共焦位移传感器。2021 年,余卿等人[22]设计一种斜照明式的彩色共聚焦光路,实现对透明材料厚度的测量。
然而,现有斜照明系统的成像面光点漂移量较大,测量精度和应用范围受限。因此,本文将现有斜照明系统的“V 字形”结构调整为三轴结构,通过增加调节支路限制光点的漂移,使其可以适应更复杂的测量条件,满足更便捷的数据处理需求,以非垂直角度获取物体的高度及透明材料的厚度特征。
2 系统原理和光路设计
2.1 经典同轴照明式彩色共聚焦原理
同轴照明式彩色共聚焦检测技术原理如图1(彩图见期刊电子版)所示,来自宽频带复色光源发出的复色光通过照明小孔被调制成点光源,通过色散管镜后,不同波长的光束在相同的介质中因折射率不同形成轴向色差,使得不同波长的光聚焦在相应的轴向位置,从而生成一系列波长连续变化的聚焦光斑。这些光束照射在样品表面,被反射后再经过分光镜和检测小孔,并最终由彩色相机接收。需要注意的是,只有聚焦在样品表面的某个波长的光束才能通过检测小孔并被彩色相机接收到,而其他波长的光束则会被检测小孔阻挡,因此在该系统中,检测小孔可以滤除杂散光和离焦光。
2.2 斜照明式彩色共聚焦测量方案
上述光路结构在测量高透射材料,如玻璃等,容易产生信号混叠,系统信号串扰大,信噪比低,无法精确获取不同表面的光学信息。针对这一问题,本文通过在彩色共聚焦系统中引入斜照明结构来解决这一问题。图2(a)(彩图见期刊电子版) 为现有的“V 字型”斜照明结构,倾斜角θ为45°。光束经色散管镜色散后,倾斜照射至样品表面,再通过物镜和色散管镜聚焦并由彩色相机接收。
然而,该光路存在光点漂移问题。具体表现为,当被测物由位置1 移动到位置2 时,聚焦在被测物表面的光斑由绿色变为红色,此时被测物表面反射的光束的中心轴线会发生偏移,从而极易使光束偏离出小孔,造成信号丢失;反映在彩色相机成像面上,即成像光点会产生漂移,如图2(b)(彩图见期刊电子版)所示,容易造成信号无法接收。
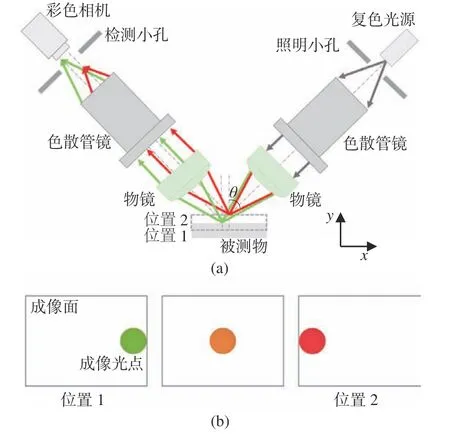
图2 “V 字型”斜照明式彩色共聚焦系统。(a) 系统原理图;(b) 光点漂移示意图Fig.2 Inclined illumination chromatic confocal system with V-shaped structure.(a) Schematic diagram of the system;(b) spot drift diagram
针对这一问题,本文提出一种解决方案,如图3(彩图见期刊电子版)所示。采用平面镜来代替采集装置,可以使被测物沿着y轴移动时,使偏离原光轴的光束原路反射回系统,从而规避了因光路变化造成的光点漂移问题。

图3 平面镜反射示意图Fig.3 Schematic diagram of the reflection by the plane mirror
在上述光路分析基础上,将现有斜照明系统的“V 字形”结构调整为“三轴结构”,通过增加上述调节支路限制光点的漂移,改进后光路图如图4(a)(彩图见期刊电子版) 所示,倾斜角θ为45°。其中,调节支路由物镜2、聚焦透镜以及平面镜组成。
在图4(a)中,宽频带光源发出的光束依次通过小孔1、色散管镜1、分光镜、物镜1,并以45°角入射到被测物表面。光束经被测物表面反射后,经过物镜2 和聚焦透镜到达平面镜表面,光束经由平面镜全反射后,再次通过聚焦透镜和物镜2,并由被测物表面二次反射,然后依次通过物镜1、分光镜、色散管镜2、小孔2,最后由彩色相机接收成像。反映在彩色相机成像面上,当被测物由位置1 移动到位置2 时,可以观察到几乎固定不动的光斑,漂移量可以忽略不计,如图4(b)(彩图见期刊电子版)所示。
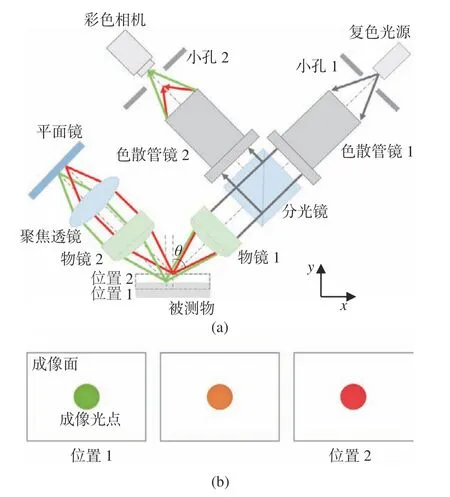
图4 改进后的斜照明式彩色共聚焦测量方案。(a) 系统原理图;(b) 抑制后的光点示意图Fig.4 The improved inclined illumination chromatic confocal measurement system.(a) Schematic diagram of the system;(b) improved spot drift diagram
2.3 斜照明式彩色共聚焦系统的理论分析
斜照明式彩色共聚焦系统源于同轴照明彩色共聚焦系统,而同轴照明彩色共聚焦系统源于传统共焦显微系统。首先,传统共焦显微系统一般采用单色光源照明。根据共焦显微理论,理想情况下系统在共焦位置处的轴向光强响应I(u)和轴向光学坐标u的关系可表示为:

其中,λ为入射单色光的波长,f为透镜的焦距,a为成像透镜的光瞳半径,u为归一化的轴向光学坐标,u可以表示为:
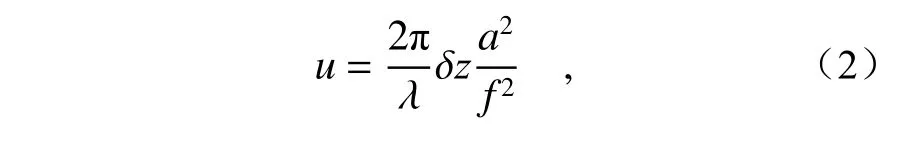
其中,δz为轴向离焦量。结合式(1) 和式(2),可以得到共焦系统的轴向光强响应函数和轴向离焦量相关。如图5(a)所示,被测表面在共焦位置处(δz=0)获得最大光强,并且光强随离焦量的增加而变小。
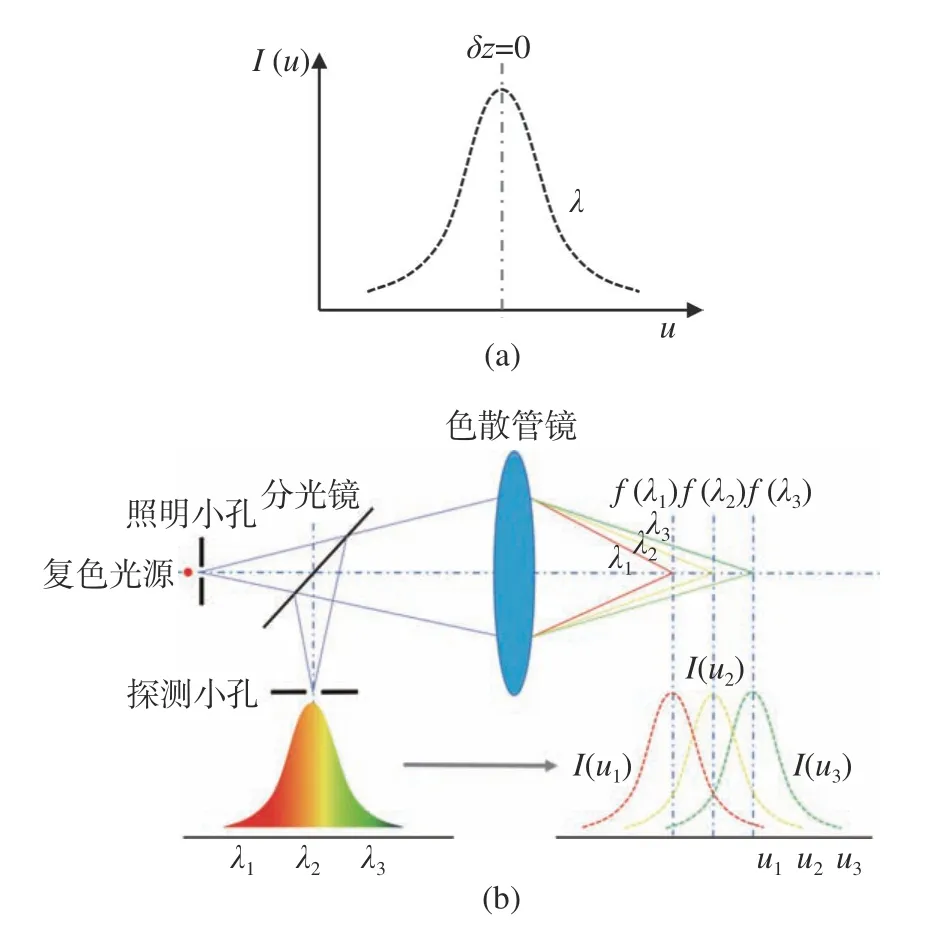
图5 不同系统的轴向光强响应。(a) 共焦系统的轴向光强响应;(b) 彩色共聚焦系统的轴向光强响应Fig.5 Axial light intensity response of different systems.(a) Axial light intensity response of confocal system;(b) axial light intensity response of chromatic confocal system.
在同轴照明彩色共聚焦系统中,一般采用复色光源照明。复色光可看作由许多种不同波长单色光叠加形成,因此其轴向光强响应是所有不同波长单色光的轴向光强响应的叠加。如图5(b)(彩图见期刊电子版)所示,每个不同的颜色波长λi对应一个轴向光强响应函数I(ui),且在其对应的焦点位置处光强信号最大,该光强信号随着轴向离焦量的增加而变小。
在理想的彩色共聚焦系统中,各波长λi与其焦点位置f(λi)呈线性关系,即f(λi)可表示为:

式中,f(λi)表示光点在光轴上的位置,λi表示光点对应的波长,h0表示线性关系的截距,k表示线性关系的斜率。
因此,在同轴照明彩色共聚焦系统中,对于两个不同颜色波长的光点,光轴向间距Δh(λi)可表示为:
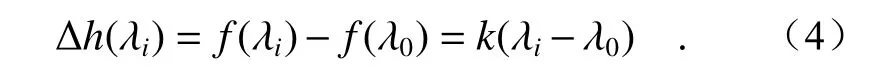
据此引申到斜照明式彩色共聚焦系统中,照明部分与被测物平面之间存在一个倾斜角θ,系统的几何关系如图6(彩图见期刊电子版)所示。
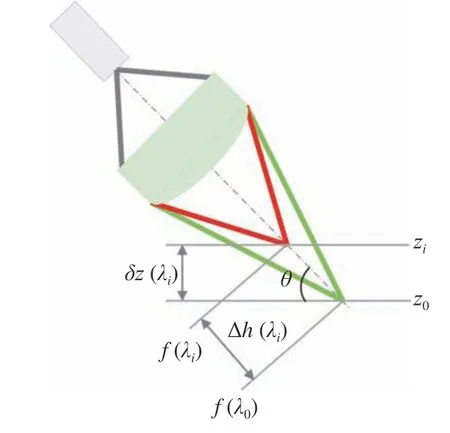
图6 轴向位移与聚焦点位移的几何关系Fig.6 Geometric relation between axial displacement and focal displacement
结合图6,根据三角函数关系可以推导出斜照明情况下聚焦点位移δz(λi)与样品z轴轴向位移Δh(λi)的关系,如下:
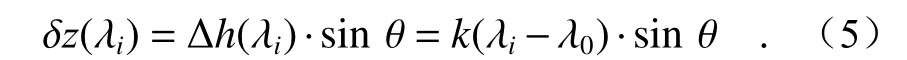
将式(3)、(4)、(5)代入式(1),可得在斜照明式彩色共聚焦系统中,在各种单色光光强一致的前提下,聚焦点处任意波长λi的光强响应函数I(λi)为:

结合本系统中一些具体的已知参数,a为色散物镜的半径,数值为20 mm,k为0.000 2,h0为30 mm,θ为45°。
假设光源在400~700 nm 的各个波长下的强度相同,利用式(1) 分别对450、500、550、600 和650 nm 波长聚焦处的轴向光强响应进行仿真,并以550 nm 波长的光线出射信号强度为标准值对其他波长进行归一化,绘制斜照明式彩色共聚焦系统的归一化光谱光强分布曲线,如图7(彩图见期刊电子版)所示。图7 中的不同颜色波长的彩色曲线代表的是不同轴向测量位置处的光谱光强分布,黑色曲线上的点是根据400~700 nm 各个单色波长的光强峰值得到的。
由图7 可以看出,斜照明式彩色共聚焦系统光谱的谱峰位置随着被测轴向位置的改变而发生移动,不同颜色的峰值波长与被测物轴向位置一一映射,因此,斜照明式彩色共聚焦测量系统具有良好的频谱选择特性,这一理论为后续的实验研究打下可行性基础。
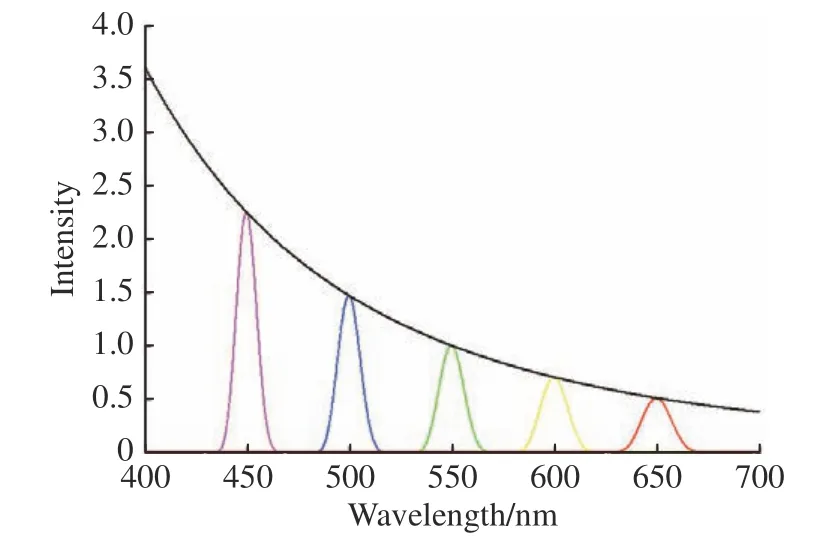
图7 不同波长位置处的光谱光强分布Fig.7 Spectral light intensity distribution with different wavelengths
2.4 颜色转换算法
本文主要通过颜色转换算法来建立被测物位移和颜色信息的对应关系。该方法将图像的颜色信息由RGB 颜色空间转换为HSI 颜色空间,如图8 所示。
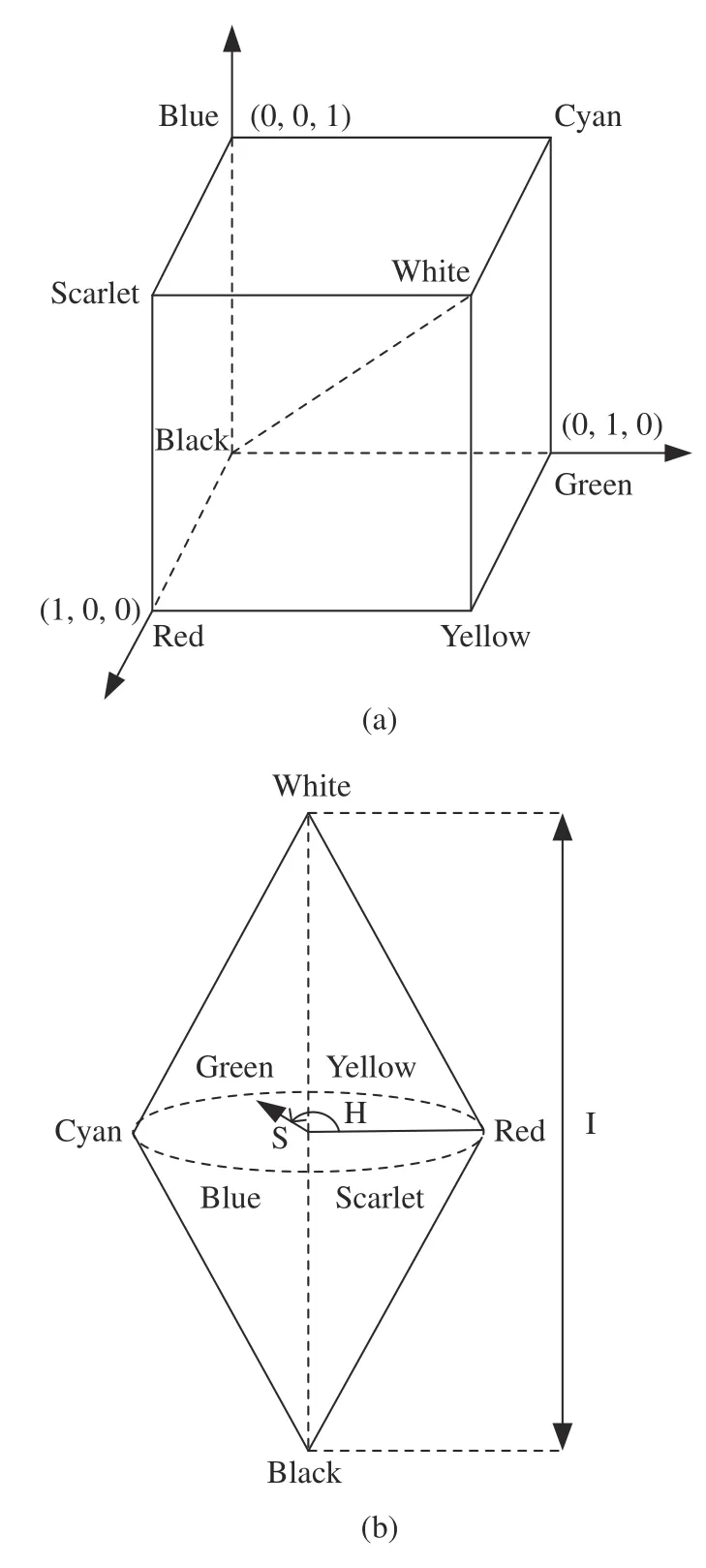
图8 (a) RGB 颜色空间与 (b) HSI 颜色空间Fig.8 (a) RGB color space and (b) HSI color space
在HSI 颜色空间中,H 值与不同颜色对应的波长存在线性关系。因此,通过对图像的颜色空间转换和H 值的提取,可以建立被测物轴向位移与图像颜色的关系,转换函数如下:
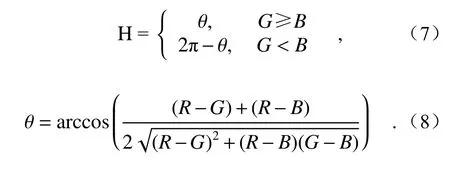
3 系统实验分析
3.1 系统搭建与标定实验
在上述理论分析的基础上,搭建了改进后的斜照明式彩色共聚焦测量装置,如图9 所示。物镜的放大倍数均为10×,NA 值均为0.2。彩色相机的型号为Balser acA2440-35uc。为了建立样品表面位置与图像颜色信息之间的关系,首先进行了标定实验。标定实验采用韦度(WD)的0 级标准量块作为被测物,利用电机驱动使其沿箭头方向直线移动。将移动步距设置为50 μm,记录0~950 μm 位移范围内的20 个位置数据,得到彩色相机成像面的颜色变化结果,如图10(彩图见期刊电子版)所示,利用颜色转换算法计算相应轴向位置处的H 值如表1 所示。

图9 三轴结构的斜照明式彩色共聚焦系统图Fig.9 Inclined illumination chromatic confocal system with a triaxial structure

图10 样品位于不同轴向位置时相机采集到的图像Fig.10 Images obtained by the camera when the specimen is at different axial positions

表1 标定实验数据Tab.1 Calibration of experimental data
根据表1,绘制出H 值与试样轴向位移的关系,如图11(a)所示。选取线性部分进行拟合,如图11(b)所示,线性范围为350 μm,拟合系数R2为0.99 以上,回归线与观测值拟合程度良好。
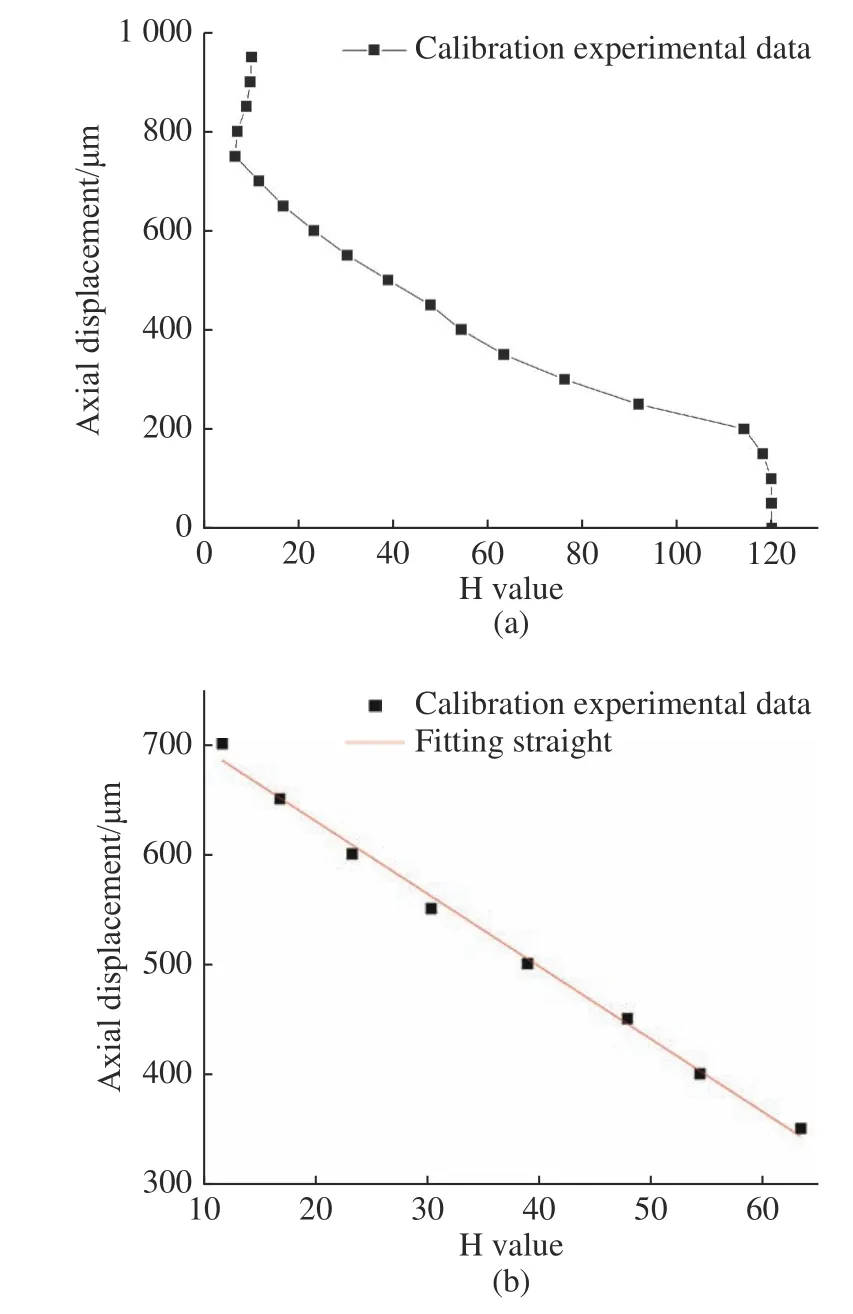
图11 标定实验。(a) 标定实验结果;(b) 线性拟合结果Fig.11 Calibration experiment.(a) Calibration result;(b) linear fitting result
经线性拟合,得到H 值-轴向位移的标定方程为:
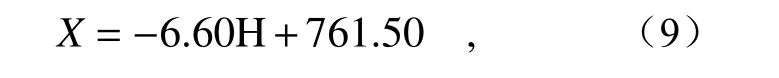
其中X表示轴向位移值,H 表示HSI 空间中相应的颜色H 值。
为了测试该系统的测量精度,首先用标定实验中1.03 mm 和1.08 mm 的标准量块搭建台阶,如图12 所示,该台阶经电感测微仪Tesa TT80 测得其实际高度为56.52 μm。测量过程中,当位移平台沿图9 所示的y轴方向水平移动时,光斑从1.08 mm 的量块表面逐渐移动至1.03 mm 的量块表面,记录分别落在两个量块表面的H 值,如图13 和表2 所示。

表2 台阶实验数据及台阶高度计算结果Tab.2 Experimental data and calculation results of step height

图12 台阶实物图Fig.12 Picture of the step
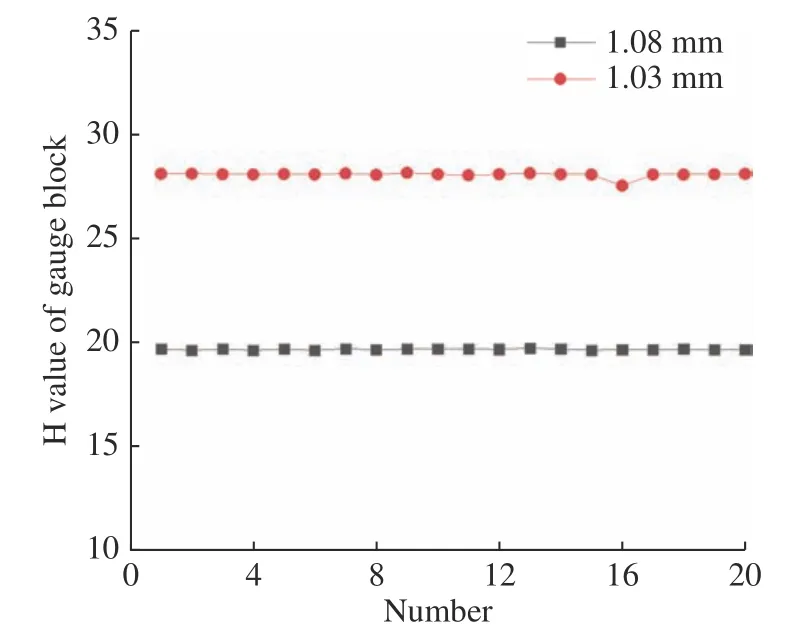
图13 量块表面H 值测量结果Fig.13 H value of gauge block
实验结果表明,20 次重复性测量得到的台阶高度值为55.44 μm,相对误差为−1.91%,3σ 值为0.37,系统的测量精度可以达到微米级别。本文中σ 的计算公式如下:
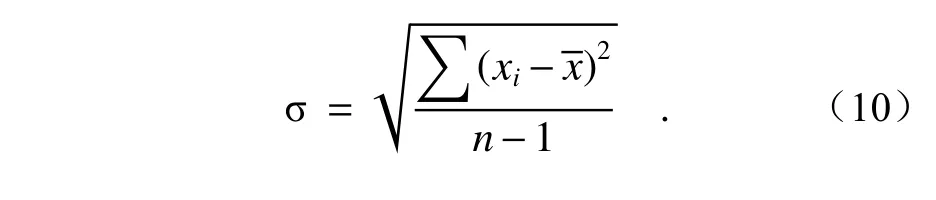
3.2 透明材料厚度测量实验
为了验证系统对透明材料厚度的测量能力,选取透射率为84% (380 nm)~ 90% (717 nm)的帆船牌载玻片作为透明材料进行测量,该载玻片经由电感测微仪Tesa TT80 测得真实值为181.08 μm。实物图如图14 所示,测量得到的颜色示意图如图15(彩图见期刊电子版)所示。图15 中左侧光点为透明材料上表面反射的H 值,右侧光点为透明材料下表面反射的H 值。

图14 透明材料实物图Fig.14 Picture of the transparent glass slides

图15 透明材料测量颜色示意图Fig.15 Color diagram of transparent specimen
同样地,在标定实验的基础上进行20 组重复性测量实验,得到透明材料厚度数据如表3所示。

表3 透明材料实验数据及厚度计算结果Tab.3 Experimental data and calculation results of transparent specimen
根据课题组已推导的透明材料计算公式(11)如下[22],
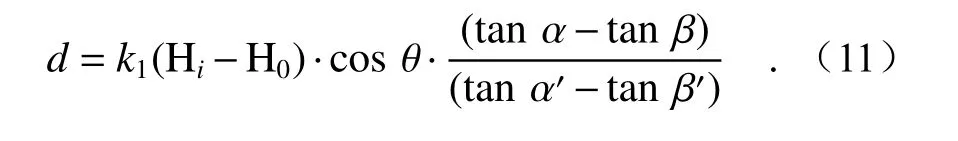
通过计算得到的透明材料厚度值为184.21 μm,相对误差为1.73%,3σ 值为1.69,系统的测量精度可以达到微米级别。
3.3 “V 字型”系统对比实验
为了证明三轴结构的斜照明系统相对于传统“V 字型”结构的斜照明系统对于光点漂移的抑制效果以及抑制后系统性能的提升,我们在相同的实验条件下将调节支路的有无视为变量,搭建相应的“V 字型”照明光路如图16 所示。

图16 “V 字型”结构的斜照明式彩色共聚焦系统图Fig.16 Inclined illumination chromatic confocal system with the V-shaped structure
3.3.1 光点漂移抑制效果对比实验
首先,在其余器件位置等实验条件不变的情况下,通过观察彩色相机在相同轴向位置处的不同成像情况,可以发现两种不同的系统成像面的光点漂移情况如图17 所示。

图17 光点漂移抑制效果对比图。(a)“V 字型”系统;(b) 三轴结构系统Fig.17 Contrast diagram of the spots drift suppression effect.(a) V-shaped structure;(b) triaxial structure
这里,以彩色相机成像面的中间位置作为基准原点,向右为正方向,以每个成像光斑的质心像素点作为中心位置,可以计算得到两种系统的光斑中心位置漂移情况,如图18 所示。通过对比可以发现,三轴结构的斜照明系统产生的成像光点漂移像素量很小,几乎可以忽略不计。
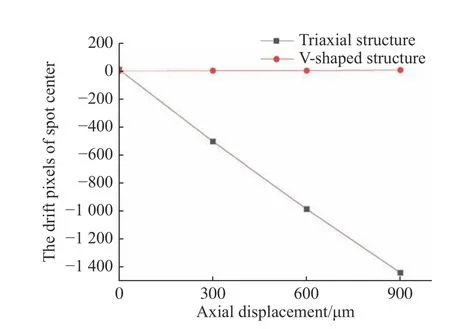
图18 光点漂移的像素计算Fig.18 Pixel calculation of the spot drift
3.3.2 “V 字型”结构系统的性能对比实验
上文提到“V 字型”结构系统的光点漂移严重,容易使光点超出彩色相机的成像范围,这是本系统的改进方向之一。下面通过实验对改进前后的系统性能进行相应的对比分析。
首先,按照3.1 节所述对改进前的系统进行标定实验,实验结果如表4 所示。根据表4,绘制出H 值与试样表面位置位移的关系,如图19(a)所示。选取线性部分进行拟合,如图19(b)所示,其线性范围为600 μm。经线性拟合,得到H 值-轴向位移的标定方程为:
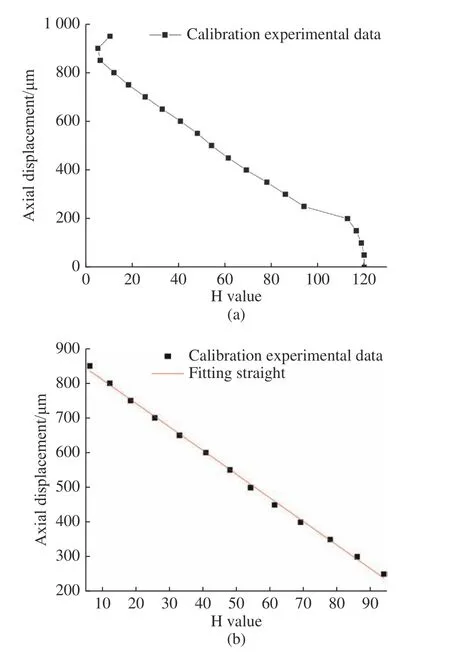
图19 改进前系统的标定实验。(a) 标定实验结果;(b) 线性拟合结果Fig.19 Calibration experiment before improvement.(a) Calibration result;(b) linear fitting result

表4 标定实验数据Tab.4 Calibration experimental data
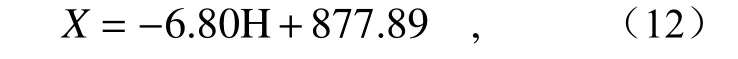
其中X表示轴向位移值,H 表示HSI 空间中相应的颜色H 值。
由于“V 字型”结构系统相较于三轴结构系统,光路折返次数减少两次,因此其测量范围增加约1 倍左右。
其次,为了对改进前后的系统性能作对比,在标定实验的基础上又分别对3.2 节和3.3 节中的台阶和透明材料进行了20 次重复性测量,其中,构成台阶的量块表面H 值测量结果如图20 所示。相同条件下测得台阶高度值为58.75 μm,相对误差为3.95%,3σ 值为1.17。
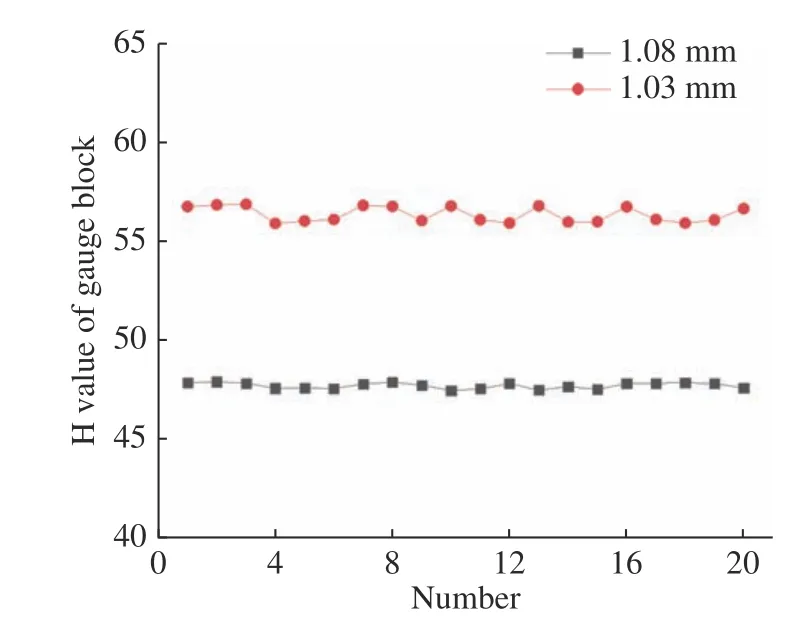
图20 量块表面H 值测量结果Fig.20 H value of gauge block
测量得到透明材料的颜色示意图如图21 所示。相同条件下测得透明材料厚度值为173.03 μm,相对误差为−4.44%,3σ 值为0.66。

图21 透明材料测量颜色示意图Fig.21 Color diagram of transparent specimen
最后,通过台阶和透明材料的测量结果对比可以发现,三轴结构的斜照明系统相较于传统“V 字型”斜照明系统,测量准确度也有所提高,系统性能上得到一定提升。
4 结论
本文提出了一种改进的斜照明式彩色共聚焦测量系统,突破了传统同轴照明彩色共聚焦系统信噪比低和光能利用率低的限制。同时对现有的“V 字型”斜照明系统进行优化,利用平面镜,增加调节支路搭建三轴结构的斜照明系统,从而达到抑制光点漂移的效果。改进后的系统应用范围更广,测量准确度更高,数据处理更为便捷。文中对斜照明系统进行相关理论分析,证明系统具备良好的谱频选择特性,并结合颜色转换算法进行实验验证系统对于台阶高度及透明材料厚度的测量能力。实验结果表明,该系统的轴向测量范围为350 μm,重复性优于1.69,测量相对误差不超过±2%,轴向测量精度可达到微米级。通过与传统“V 字型”结构斜照明系统的对比证明,本文提出的系统具有良好的光点漂移抑制效果,且在系统性能上也有所提升。然而,本文提出的系统体积仍较大,稳定性有所欠缺。未来将简化硬件结构,将系统朝微型化、精密化的方向发展,以进一步提高系统的量测精度和稳定性。
