大规模超环神经网络分岔动力学

张跃中 肖 敏 王 璐 徐丰羽

众所周知,神经网络在信号处理、自动控制、联想记忆、人工智能[1]、生物医学治疗等领域有着广阔的应用前景,这些基本应用在很大程度上依赖于神经网络的动力学特性.由于神经网络动力学是生物生理学和非线性动力学的交叉学科,研究其稳定性、振荡、分岔、混沌和同步等多种动力学行为具有生物学和动力学意义[2].一般来说,神经网络具有大规模的非线性动力学性质和复杂的行为,为进一步把握神经网络的动力学本质,大批研究者将研究重点放在简单的神经网络模型上[3-5],为寻求大型复杂神经网络的研究方案做铺垫.例如,在文献[3]中,作者提出了3 个神经元的神经网络模型;文献[4]研究了7 个神经元的神经网络模型;文献[5]研究了具有双向联想记忆五维神经网络.显然,如果仅仅研究一个简单的网络,一些复杂问题可能会被忽略,并且在现实生物学中神经网络以及网络的构建模型都是错综复杂,多种多样的.因此,本文提出一类大型神经网络的研究是极具理论价值和实践价值.

在如神经网络、生物模型和进化生态学等大多数实际的动态网络中,时间延迟的存在是难以避免的.然而,由于时滞的存在,系统可能变得不稳定,系统的动态行为变得更加复杂.在神经网络中,由于突触中信号传播速度和处理时间的有限性,不同相邻神经元之间的通信存在时滞差异.人们对研究具有时延的神经网络的动力学越来越感兴趣,理论成果也相继发表.因此,以时滞(离散时滞[6]、分布式时滞[7]、多时滞[8]、泄露时滞[9-11]等)作为研究对象,分析神经网络的特性和动力学以及控制时滞系统的动态行为是十分必要和重要的.

在动力系统中,可通过分岔方法获得某些丰富的动力特性,这是无可争辩的.分岔方法的优越性在于能捕捉复杂系统的内在性质,涉及振荡行为出现的分岔可以帮助理解网络中观察到的参数敏感性,并提供有利于网络的信息[12-14].例如,对于带有抑制的环结构遗传模型,其渐近行为得到广泛的检验.大肠杆菌循环抑制网络模型的建立[15]就是很好的体现.分岔的种类也有很多种,其中随着参数的变化,系统在稳定与不稳定之间切换的平衡点被称为Hopf 分岔点[16].近年来,对神经网络有关Hopf分岔分析进行了大量的数学研究,人们可以通过Hopf 分岔的深入而清晰的认识某个网络,可以提供有用的网络信息,为网络的应用提供更多的可能性.因此,研究神经网络的Hopf 分岔具有重要意义.此外,Hopf 分岔可以由延迟诱导的生物系统是如何表现出周期性响应,更准确地说,由时间延迟引起的Hopf 分岔可以得到一些有趣的结果,如延迟与振荡幅度的关系.还有研究表明,这些Hopf 分岔分析有助于生物视觉信息的快速处理,并可用于预测大脑的病理状态.

显然,具有时滞依赖的高维神经网络的动力学特性是值得研究的,但影响其动力学的因素很多,其中网络结构也是关注的因素之一.众所周知,约有1 000 亿个神经细胞组成了人的大脑,每个神经细胞可长出2 000 至数万个树突与其他神经细胞连接.然而人脑的开发仅有1%,倘若能进一步的开发或者未来通过人工神经网络来学习生物神经网络将是极具意义和价值的.在人脑和脊柱中,大量的神经元构成一个大型的复杂神经网络,通过网络的结构特性也可以简单地剖析成放射状网络、链状网络和环状网络等.因此,以结构作为研究点是极具代表性和研究价值的.例如Xiao 等[17]提出了具有辐射状的神经网络模型;Bootan 等[7]和Huang 等[18]研究了具有单环状的神经网络模型.其次,科研者更多提出的是形式单一且结构简单的网络,依旧缺少具有多类网络结构组合的大型网络.为此,本文提出一类融合多种结构的超环神经网络模型.如图1示,由超多环形网络组合的大型神经网络图,即体现了神经网络的环状、辐射状,也可简化到链状形态.此外,研究这些简化的连通性结构的目的是进一步理解具有更复杂连通性的递归网络行为的机制,以及研究复杂网络中相互连接的模式,即网络基序[19],对于了解整个网络的动态行为是非常重要的.

在上述研究基础上,本文提出一类基于时滞诱导且融合了多种结构和高维性的超环神经网络,对该类网络的稳定分析及分岔现象问题进行研究.本文的主要贡献如下:

1)提出一类高维超环神经网络,该网络不仅融合了多类结构,也体现了一般性.

2)针对大型神经网络,选用离散时滞作为分岔参数,讨论其网络所带来的新型稳定性及分岔理论.

3)引用矩阵与线性方程组的图解法,解决一类规则性高维复杂网络模型的特征方程问题.

1 建立结构型高维神经网络模型

本文研究了多时滞诱导的具有n2个神经元组成的一类复杂的神经网络.针对该网络,首先绘制出简化的神经网络模型图(见图1),对应的数学表达式如下:

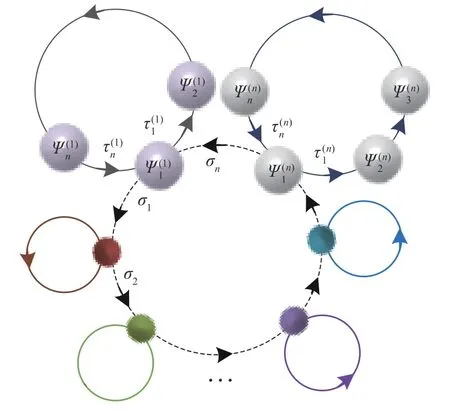
图1 一类融合多种结构的超环神经网络模型图Fig.1 Model diagram of a class of super multi ring neural network fused with multiple structures

注 1.生物神经网络具有多姿多态、复杂多变的特性,仅对辐射状或环状网络模型的研究与实际神经网络还有一定差距.因此,有必要构建一类有机复合多种结构的一般性网络.网络(1)的提出融合了环型和辐射状的结构,并将低维扩展到高维,使其能更准确地描述真实神经网络.

本文主要研究大型神经网络(1)的稳定性和分岔问题.建立网络(1)的分岔条件,并讨论时滞、结构对网络(1)分岔的影响.为推论出网络(1)的有关稳定性和分岔现象的基本结果,需要并可以作以下假设.

假设 1.

显然,由假设1 可得,网络(1) 具有平衡点O(0,0,···,0)1×n2.

注 2.网络(1)是高维多时滞系统,拥有不唯一的平衡点.即,除了平凡平衡点O(0,0,···,0)1×n2外,可能还有其他平衡点.本文重点研究原点O(0,0,···,0)1×n2邻近的局部动力学行为,比如局部稳定性和Hopf 分岔.关于其他平衡点的动态演化行为,可以通过坐标变换将平衡点平移到原点,之后的处理方法类似.因此,仅讨论原点的局部动力学特征是具有代表性的.

假设 2.

注 3.由于神经元间连接强度、突触等因素的影响,信息传输的时间延迟不同.网络(1)很好地体现了信息传输时滞的相异性.本文重点研究神经网络的环状结构.因此,假设2 展现了外环和中心环的时滞和是相等的.这样既可以简化模型分析,又可以很好地保留环状特性.

2 局部稳定性和Hopf 分岔

本节研究时滞对网络(1) 稳定性和分岔的影响,并从数值分析上准确地确定分岔点与时滞的关系式.针对网络(1),基于假设1 可得到在平衡点处线性化模型为

注 4.已知系统的局部稳定性和Hopf 分岔阈值取决于系统的一次项部分.因此,对网络(1)进行线性化处理,期望得到其稳定性条件和分岔判据.

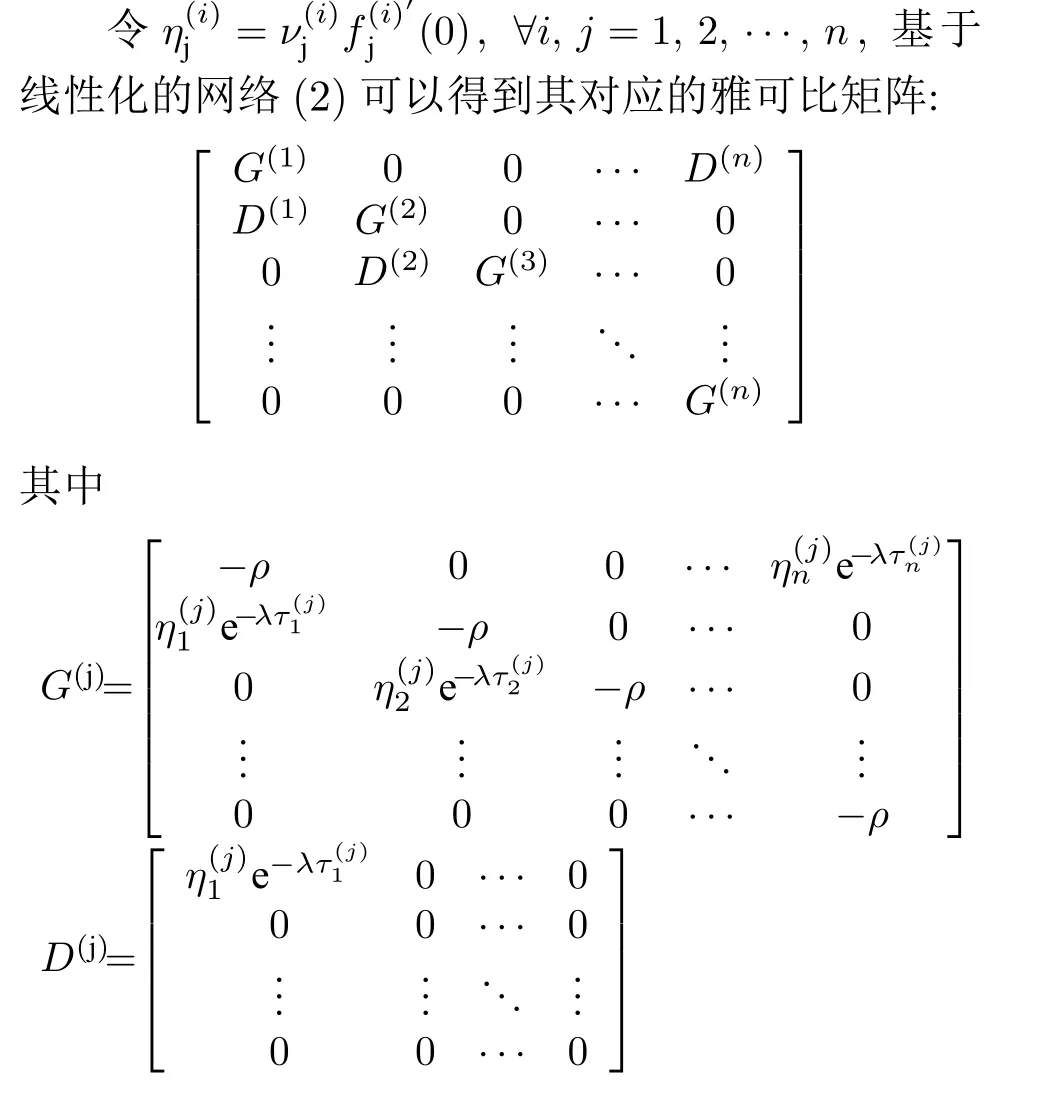
针对该雅可比矩阵,利用矩阵与线性方程组的图解法[20]并给出如下引理.

2.1 无时滞状态

当τ=0 时为无时滞状态,在此状态下判断系统的初始稳定情况.因此,特征方程(3)可退化为:

引理 2.当满足条件ΔI ＞0,(I=1,2,···,n2)时,式(5)的所有根都分布在坐标轴的左半平面.

证明.由赫尔维茨判据[21]可知,若某特征方程各项系数所构成的主行列式及其顺序主子式都为正,则该特征方程的解都是具有负实部的解.因此,利用赫尔维茨判据,由 ΔI ＞0,(I=1,2,···,n2)易得式(5)的所有根都分布在坐标轴的左半平面.

2.2 有时滞状态

由第2.1 节可知,在无时滞状态下可以判断出网络的初始状态是否稳定,进而随着时滞的引入,分析总结出网络稳定性及分岔的条件.首先,在时滞状态下令ξ(λ)=(λ+ρ)neλτ对式(4)进行简化,可得:

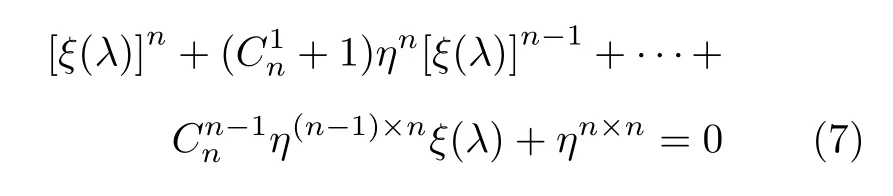
由于ξ(λ)前的系数是已知常数,所以可定义ξj(λ),j=1,2,···,n为式(7)所对应的n个解.其次,为寻找临界值(分岔点),需找取式(7) 的纯虚根,进而假设λ=iω.令ξj(λ)=αj+iβj,∀j=1,2,···,n代入式(7),整理可得:

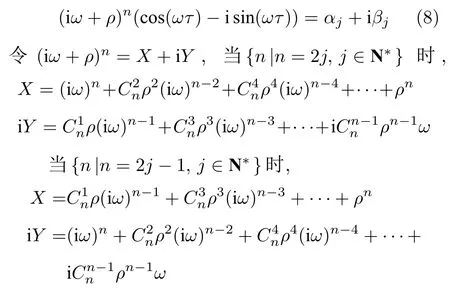
显然,式(8)是一个ω的复值等式,为了解决未知变量ω和τ的问题,可以将式(8)分解成实部部分和虚部部分,拆分的等式如下:

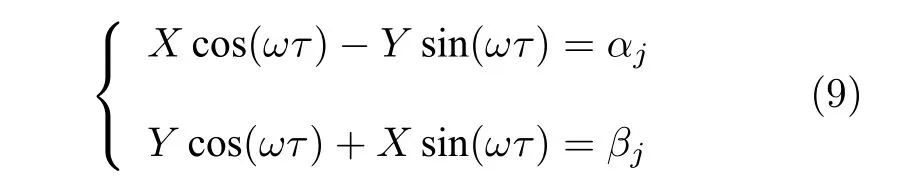
针对式(9),利用克拉默法则容易推得:

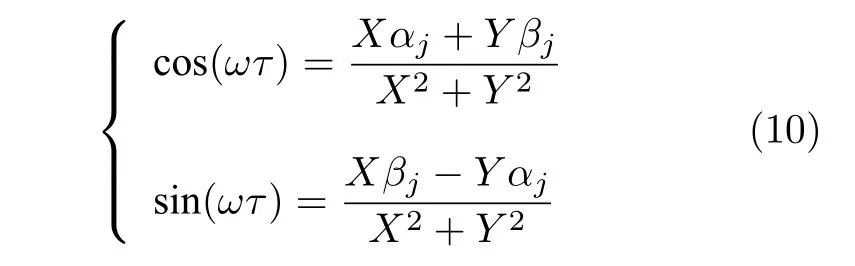
由 cos2(ωτ)+sin2(ωτ)=1 可推得:

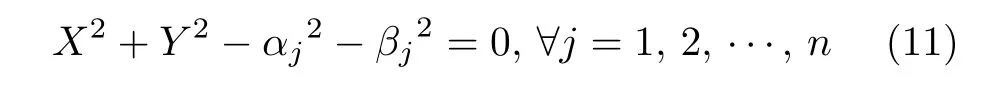
取ε=ω2,对式(11)进行展开整理得:

其中,Ak,∀k=1,2,···,n-1 为式(11)展开式有关ε的系数.在此,定义h(·)函数 :

3 数值算例与仿真

本节使用一个数值例子来仿真验证所得到的理论推导.神经网络中激活函数常用 t anh(·)表示.考虑以下系统:

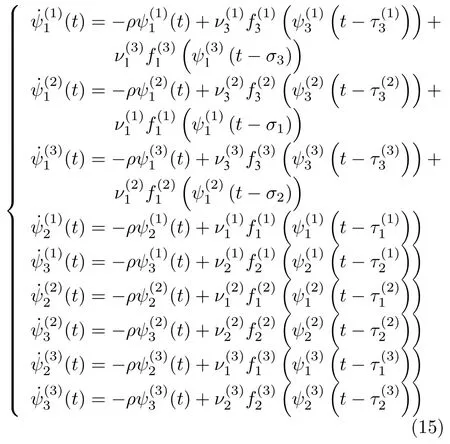
然后,给出数值仿真所需的初始参数(见表1).

表1 网络(15)的初始参数设定表Table 1 Initial parameter setting table for network (15)

本节讨论时滞对网络(15)稳定性和分岔的影响.首先,根据第2 节理论推导出分岔点τ0=3.22 s,其次,验证无时滞时网络(15) 的特征方程子行列式的值是满足引理1 的假设.最后,根据定理1可知,当选取时滞为τ=3.15 s＜τ0时,网络(15)是稳定的,显然图2 的仿真图是对应的,可以看到网络在平衡点附近是渐近稳定的.当τ=3.3 s＞τ0时,仿真结果见图3,网络的平衡点不稳定,并且明显地可以观测到相图中出现了极限环.显然,数值仿真的结果本文的结论是相统一.说明所得的分岔结果是非常精确和有效的.

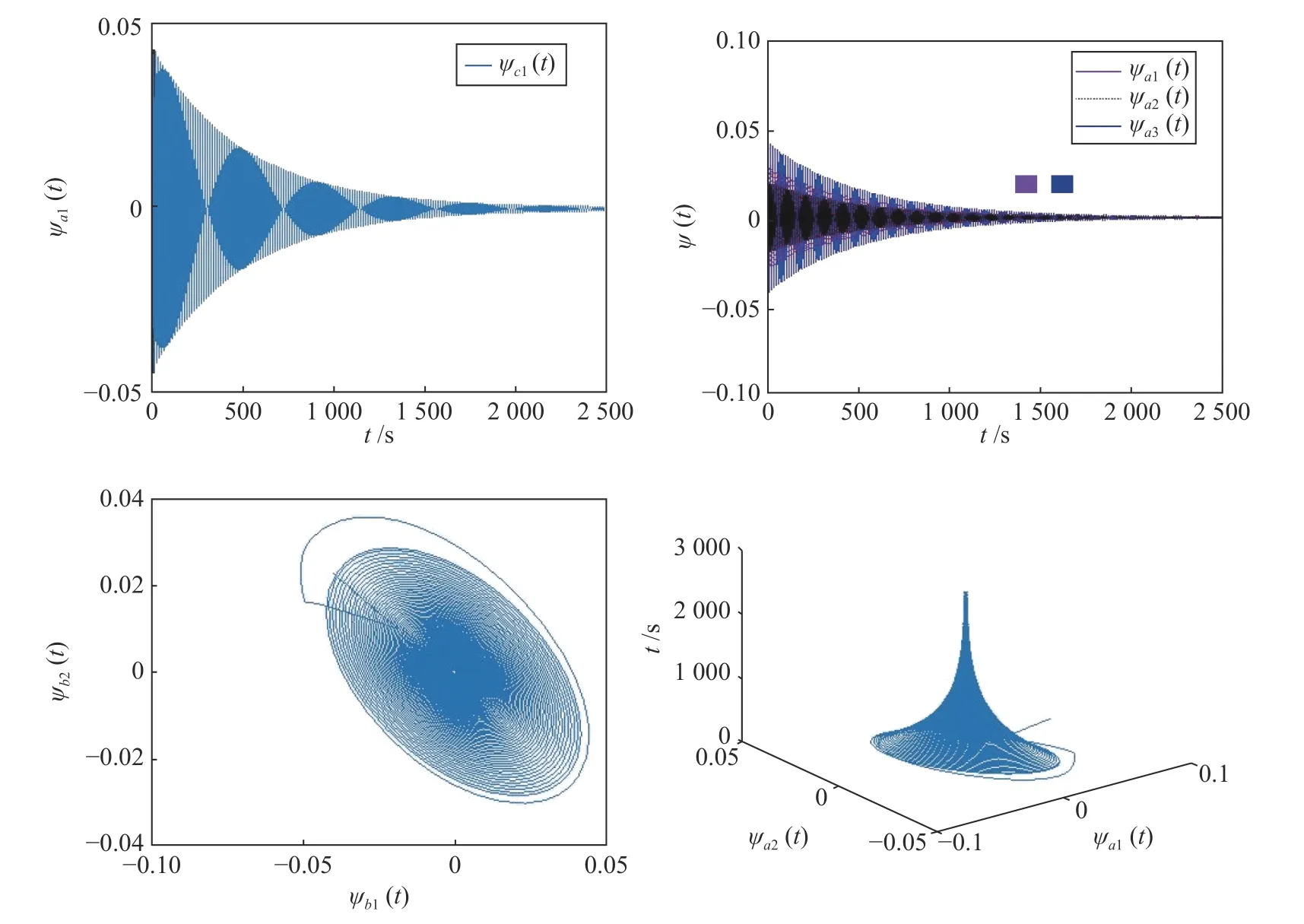
图2 当 τ=3.15 s ＜ τ0时,网络(15)渐近稳定Fig.2 When τ=3.15 s ＜ τ0,network (15)is asymptotically stable

图3 当 τ=3.3 s ＞ τ0 时,网络(15)失稳Fig.3 Network (15)is unstable when τ=3.3 s ＞ τ0

本文研究大规模超环神经网络的动力学演化行为.进一步,通过数值仿真给出环的个数和神经元数量对神经网络分岔的影响规律.选取表1 中的自反馈系数ρ和耦合连接权重,并假设外环神经元个数为3.表2 展现了网络结构对稳定性和分岔的影响.显然,随着环数和神经元数量的增加,分岔点逐渐减小,即稳定阈值变小,Hopf分岔将提前发生.这意味着网络规模越大,环状结构越多,系统的稳定性越差.

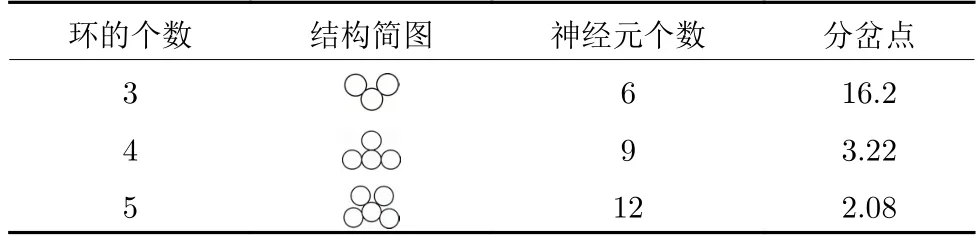
表2 结构变化影响分岔点位置情况表Table 2 Table of the influence of structural change on the location of bifurcation points

4 结论

本文选取时滞作分岔参数,研究了一类大规模超环神经网络的稳定性与分岔动力学.研究重点主要包括以下3 个方面:1)将简单的单环神经网络模型推广到一般的大规模多环网络模型;2)通过分析特征方程根的分布情况,给出了网络的稳定性及产生分岔现象的条件;3)揭示了网络规模和环的个数对网络动力学的影响规律.

超环神经网络模型的提出及研究是具有前瞻性的,此外,未来研究工作的延伸和方向性的指导将更有助于实际神经网络的应用.为此,后续将开展以下工作:1)考虑双向连接及多类型时滞融合的大规模神经网络的分岔动力学;2)将整数阶神经网络推广到分数阶神经网络,研究阶次对动力学的影响;3)设计可行控制策略,优化神经网络的动态演化过程.