一种针对德州扑克AI 的对手建模与策略集成框架
2022-05-28臧一凡兴军亮
张 蒙 李 凯 吴 哲 臧一凡 徐 航 兴军亮
计算机博弈与人工智能的发展一直相辅相成.自人工智能(Artificial intelligence,AI)学科诞生伊始,计算机博弈研究就是AI 技术发展创新的沃土,AI 领域的先驱图灵和香农都曾研发过计算机博弈程序[1].用于测试机器是否具有 “智能”的图灵测试,其实现形式就是通过人和机器之间博弈进行的.智能博弈一直都是衡量AI 技术发展水平的重要评价准则,AI 发展历史上的主要里程碑事件都与计算机智能博弈游戏研究相关.1962 年6 月机器学习之父阿瑟·塞缪尔的西洋跳棋程序战胜美国著名职业选手尼雷、1997 年5 月IBM 公司的超级电脑 “深蓝”战胜国际象棋大师卡斯帕罗夫等,都是AI 学科早期发展历史上重要的里程碑事件.
近年来,计算机的存储与计算能力不断提升,以及各类数据的爆炸式增长与积累,以人工神经网络为主要技术工具的深度学习方法[2-3],因其强大的数据拟合能力与泛化能力,使其在语音识别[4]、图像识别[5]和自然语言处理[6-7]等领域都取得了突破性进展,成功推进了AI 领域由感知智能到认知智能的跨越.如今,AI 领域正在经历从认知智能迈向决策智能的过程,以强化学习与深度学习相结合的深度强化学习方法[8-10],在围棋博弈领域取得了重大突破并成功打败人类顶尖选手[11-15],为完美信息场景下的博弈决策问题提供了有效的方法指导.而智能体如何在其所处状态信息不完全已知的情况下做出准确的决策,是目前AI 领域面临的核心问题.因此,不完美信息博弈场景下智能决策问题的研究和解决,是AI 取得突破的核心前沿领域和重要驱动力.
游戏是一种虚拟的实验环境,具有可控损失的优点,实验成本低且允许实验失败.博弈游戏本身又存在很多难点,具有决策空间复杂、实时高动态、信息不完美等特点[16-17],能够为智能决策问题研究提供一种良好的算法实验环境,是AI 技术绝佳的实验研究平台.不完美信息博弈游戏是指智能体在游戏中只能够获得自身的游戏状态以及公共游戏信息,而无法掌握全部的局面信息[18],例如在德州扑克[19-20]、麻将[21]、斗地主[22]等游戏博弈过程中对手的手牌不可见,因此获得的局面信息是不完美的,这也使此类博弈游戏的研究和解决更具挑战性.
现实生活中,在军事、经济、商业、网络安全等实际场景中的大多问题,均属于不完美信息博弈问题.此类问题的研究和解决往往受到实际环境的成本制约,而将其转化为对博弈游戏抽象模型的求解寻优问题可以大幅降低所需实验成本.因此,以不完美信息博弈游戏为载体的研究,能够为现实问题的解决提供有效的方法论.
本文选择德州扑克游戏作为对不完美信息博弈的主要研究和实验对象,以演化学习方法[23]和深度神经网络相结合完成对智能体的训练,通过在线的对手风格建模和种群策略集成的方法使智能体能够适应对手策略变化,最终实现一种轻量高效并对解决不完美信息博弈问题具有通用性的博弈求解框架.
1 德州扑克游戏
德州扑克游戏规则明晰、玩法多样且趣味性很强,是最受欢迎的扑克游戏之一.德州扑克游戏具有信息不完美、状态和动作空间巨大、对手不确定等特性[24],是不完美信息博弈游戏的典型代表,集中反映人工智能领域的许多核心问题,其研究对于整个人工智能领域的发展有着极其关键的影响,得到国内外诸多研究团队的极大关注并取得诸多进展.
1.1 游戏规则介绍
德州扑克游戏通常采用52 张扑克牌,参与游戏的玩家人数通常限制在2~ 9 人.游戏分为翻牌前、翻牌、转牌和河牌4 个阶段,在翻牌前阶段开始时,每名玩家将获得2 张只有自身能够看到的 “底牌”,之后的3 个阶段开始时桌面上会分别发出3 张、1 张和1 张 “公共牌”.在经过各阶段游戏多次的 “加注/全压”、“跟注/过牌”、“弃牌”等押注圈操作后,若牌局仍存在至少两名玩家没有弃牌,游戏进入 “摊牌”阶段,该阶段各玩家在自己的2 张底牌和5 张公共牌中挑选5 张形成牌组,按照图1 所示的德州扑克游戏牌型大小规则分出胜负,赢家获得桌面上全部筹码.

图1 德州扑克游戏牌型大小规则Fig.1 Texas Hold'em card rules
本文主要针对两人无限注的德州扑克游戏(Heads-up no-limit Texas Hold'em,HUNL)进行方法的实验和验证.HUNL 是指只有两个玩家参与的德州扑克游戏,游戏双方按照游戏位置分为大盲位和小盲位.小盲位在翻牌前阶段首先做动作,其余阶段均为大盲位首先做动作.每局游戏结束时双方交换游戏位置并且重置总筹码量,然后开始下一局游戏.
1.2 相关解决方法介绍
HUNL 方面的研究主要经历从博弈树模型搜索优化逼近纳什均衡策略,到深度神经网络拟合纳什均衡策略,再到深度强化学习自我博弈优化的发展过程.
Slumbot[25]是博弈树模型搜索优化方法的典型代表,其核心是利用反事实遗憾最小化(Counterfactual regret minimization,CFR) 算法[26]在HUNL 中逼近纳什均衡策略.Slumbot 主要算法流程为:首先根据HUNL 规则构建出游戏的博弈树原始模型;然后利用抽象技术[27]将相似游戏状态进行聚类,从而缩减博弈树规模,降低算法计算规模;最后在缩减过的博弈树上进行蒙特卡洛反事实遗憾最小化(Monte Carlo counterfactual regret minimization,MCCFR)算法[28]迭代,最终收敛得到近似的纳什均衡策略.这种方法严重依赖于游戏博弈树模型和人类专家知识进行抽象,并且CFR 算法需要对博弈树上约6.31×10164个状态结点进行不断地采样遍历和迭代优化从而收敛得到纳什均衡策略,即使经过模型缩减后该方法仍需要耗费大量的计算和存储资源,例如Slumbot 在训练阶段需要耗费大于105个CPU 小时的计算资源和TB 级别的存储资源来分别迭代优化和离线保存策略.此外,CFR 算法最终收敛得到的是一种静态的离线策略,所以在对手策略变化时存在无法动态适应和剥削对手等问题.
DeepStack[29]是利用深度神经网络拟合纳什均衡策略方法的典型代表,其核心主要是利用CFR+算法[30]迭代计算出部分游戏状态对应的纳什均衡策略,然后使用神经网络对采样到的 “状态-策略”样本进行拟合,并利用神经网络的泛化能力,估计得到没有采样过状态的策略信息.此类方法的性能主要依赖于采样到的样本数量和神经网络拟合精度,比如DeepStack 需要在每个阶段游戏中至少采样106种游戏状态,并在博弈子树上进行至少103轮算法迭代从而得到神经网络训练样本,这至少需要耗费106个CPU 小时和103个GPU 小时的计算资源,因而该方法需要极其巨大算力支持,导致其运算经济性较差,并且训练样本的存储也需要耗费大量的存储资源.此外,在与对手实际交互过程中,DeepStack 每次决策均需要在博弈子树上进行算法迭代以求解均衡策略,存在决策速度和算法性能的矛盾性问题.
神经虚拟博弈(Neural fictitious play,NFSP)[31]是基于深度强化学习自我博弈优化方法的典型代表,其核心思想是通过自我博弈对战提升策略性能,算法训练过程中博弈双方每次固定其中一方策略,利用强化学习算法通过在线博弈优化另一方策略,交替进行获得策略提升.此类基于强化学习的方法需要不断采样大量的交互数据并保存到经验回放池[32-33],从而给神经网络的训练优化提供样本.NFSP 在训练时需要至少采样约3×107组交互样本,并且强化学习训练存在样本利用率问题.此方法目前仅适用于小规模博弈问题和简化的德州扑克游戏中,在大规模和多人博弈问题中存在算法稳定性差和无法快速收敛到纳什均衡解等问题.
上述HUNL 的主流求解方法均是为得到近似的纳什均衡策略,从而在理论上保证自己不输.但是对于德州扑克这种具有巨大状态和动作空间的不完美信息博弈游戏,求解近似的纳什均衡策略不仅在计算层面是非常困难的,而且计算结果与真实纳什均衡之间的差异也很难衡量.此外,由于在HUNL 中纳什均衡策略的静态特性,智能体只是根据已知信息使用固定响应作为自身策略,忽略了对手行为对自身策略的影响,所以无法根据对手的实际特点发现和利用对手弱点,进而实现自身收益最大化.
此外,演化学习在德州扑克游戏中得到过成功应用,ASHE[34]是此类方法的代表.ASHE 首先根据人类玩家知识定义具有特定策略规则的对手,然后通过智能体种群同时与不同对手进行对打和演化训练,从而不断提升种群对特定对手的适应度.由于ASHE 博弈水平与训练对手的种类及策略水平相关性较强,因此智能体训练时需要面对博弈类型尽量丰富的对手,而该方法中对手智能体是根据常见玩法策略经过人工精心设计得到,使该方法对人类专家知识的依赖较为严重.并且在博弈过程中,ASHE 需要依赖一种规则的决策算法得到其策略,无法端到端完成该过程.
2 方法框架
针对第1.2 节中各类HUNL 主流求解方案所存在的缺点,本文设计了不完美信息博弈求解框架流程图(见图2).本框架将演化学习方法和深度神经网络相结合,通过在线的对手风格建模和种群策略集成使智能体能够适应对手策略的变化.
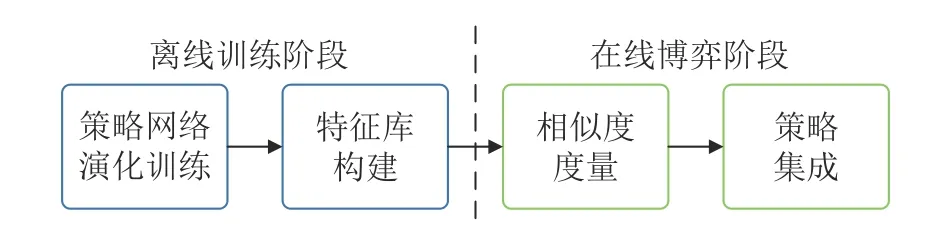
图2 不完美信息博弈求解框架整体流程Fig.2 Overall process of the imperfect information game solving framework
本框架整体分为智能体的离线训练和在线博弈2 个阶段,主要包含以下4 个步骤:
1)首先通过智能体与已知风格的对手博弈交互,完成智能体策略神经网络参数的种群演化训练,获得能够剥削不同风格对手的克制策略网络;
2)然后利用不同克制策略网络重新构建智能体,并分别与其对应克制对手博弈交互,通过在交互过程中收集对手信息来构建出对手特征库;
3)在线博弈阶段,首先对未知对手在线建模,并与对手特征库进行博弈风格的相似度度量,得到博弈风格度量矩阵;
4)然后根据博弈风格度量矩阵对各种克制策略网络的输出进行加权集成,从而获得集成策略与对手进行博弈交互.
2.1 离线训练阶段
智能体的离线训练阶段主要是为了获得能够剥削已知风格对手的策略网络并构建对手特征库.本阶段首先设计含有不同博弈风格的对手池和能够在线建模对手的智能体结构,然后通过智能体与对手池中的不同对手进行博弈交互,从而利用种群遗传算法对智能体策略网络参数进行演化训练.
1)博弈风格建模与对手池设计
为保证集成策略在面对不同对手时均具有一定适应性,每种克制策略应尽量均匀分布在整个策略空间中,因此对手池应为策略网络的种群演化训练提供具有不同典型博弈风格的对手策略.
根据上述要求,首先对德州扑克游戏人类专业玩家的常见策略和博弈风格进行充分调研和总结,最终从德州扑克游戏代表性玩法的 “策略激进度”和 “手牌松紧度” 两个维度出发,在整个策略空间中定义不同风格的对手策略从而构建对手池.“策略激进度”评价玩家在不同牌局状态时动作的概率分布情况,激进类玩家即使在游戏局势不足够有利时,选择加注动作的概率也比较高,而在相同情况下保守类玩家弃牌的概率较高.“手牌松紧度”评价玩家所玩手牌的牌力范围,若玩家只在手牌牌力较大时继续游戏,手牌较小时选择弃牌,则表示其博弈风格比较 “紧”,如果玩家即使在手牌牌力相对较小时也将游戏进行下去,则表明其博弈风格比较 “松”.
根据上述博弈风格的度量方法得到了如图3 所示的对手池策略空间,并将不同风格的玩家策略归类为 “松-弱”、“松-凶”、“紧-弱”和 “紧-凶”四类博弈类型.“松-弱”和 “松-凶”型玩家具有较 “松”的手牌松紧度,其手牌牌力范围一般大于40 %,“紧-弱”和 “紧-凶”型玩家则具有较 “紧”的手牌松紧度,其手牌牌力范围一般小于40 %.“松-弱”和“紧-弱”型玩家具有偏保守的策略激进度,表现出跟注动作较多和加注动作较少等特点,“松-凶”和“紧-凶”型玩家的策略则偏激进,表现出加注动作较多和跟注动作较少等特点.

图3 对手池策略空间与博弈风格类型定义Fig.3 The opponent strategy space and game styles definition
2)智能体结构设计
为获得能在博弈交互过程中建模对手的智能体,本文设计了图4 中右图所示的智能体结构,该智能体主要由特征提取器和策略网络2 个模块组成.

图4 离线训练阶段算法流程及智能体结构Fig.4 The offline training process and the agent structure
特征提取器主要在博弈交互过程中从游戏的游戏牌局上不断收集与对手的历史交互信息,然后统计获得对手在不同牌局状态时的特征信息,并作为对手特征输入智能体策略网络,从而完成对手建模任务.德州扑克是一种参与人之间动作具有先后顺序的动态博弈过程,适合使用博弈树对该类型的博弈进行表示.而特征提取器就是一种与博弈树类似的树形数据结构,树中结点代表不同的游戏牌局状态,结点之间连接的边代表不同的动作,每个结点上都将维护对手历史博弈交互信息的特征值.
牌局状态主要是由两名玩家交互的动作序列决定的.特征提取器的构建是根据游戏历史动作序列进行动态 “扩充”和 “更新”的过程.例如:当特征提取器已经存在动作序列 “加注300/加注600/跟注”,如果另外两局游戏的动作序列分别为 “加注300/加注600/跟注”和 “加注300/加注600/加注900”,那么对于已有的状态结点 “跟注”,特征提取器将只对该路径结点记录的特征进行更新.而对于不存在的状态结点 “加注900”,特征提取器将扩充自身结点.由于德州扑克游戏动作空间巨大,为了控制树形结构的规模,对游戏双方均进行了动作抽象,并按照底池倍数将加注的筹码量映射到以下7 个范围内:(0,0.125)、(0.125,0.375)、(0.375,0.75)、(0.75,1.25)、(1.25,2.0)、(2.0,4.0)、(>4.0).
智能体策略网络主要是完成 “状态特征-动作策略”的端到端映射过程,结构如图4 所示,由对手特征网络、游戏特征网络和策略输出网络三个模块组成,其中对手和游戏特征网络均是由多层长短期记忆网络(Long short-term memory,LSTM)所构成,图中每个LSTM 区块均对应其中一层,而策略输出网络则是由包含多个隐含层的全连接神经网络组成.
博弈过程中智能体每次做动作时,首先根据当前的游戏牌局提取出游戏特征,并根据牌局状态得到在特征提取器中对应结点位置,从而读取得到结点上维护的对手特征.然后将游戏特征和对手特征构建为特征向量,并分别输入对应的特征网络进行特征编码.最后,2 种特征网络输出的编码信息 “拼接”后输入策略输出网络,策略输出网络输出智能体策略并与对手博弈交互.详细特征及编码方式见第3.1 节特征定义部分.
3)种群遗传算法
在德州扑克这种对抗性的回合制不完美信息博弈游戏中,由于对手策略未知并且动态变化,导致深度强化学习算法在这种具有较高随机性环境中的训练难以收敛.遗传算法通过模拟生物界 “优胜劣汰,适者生存”的进化法则,在整个解空间内不断搜索具有最高博弈性能的智能体策略并繁衍新的种群,使得种群适应度得到稳定的提高,最终以轻量化的算法框架获得良好的收敛效果.本文基于遗传算法的思想对智能体种群进行演化训练,训练核心算法流程如图4 所示,主要包括以下3 个步骤:
a)选择.选择是为了筛选并 “淘汰”种群中适应度较低的个体,适应度较高的个体将存活至下一代种群.本步骤首先将种群每个智能体分别与所指定的对手进行博弈交互,然后对每个智能体的适应度进行评估,最后种群内所有智能体将根据其适应度高低进行排序,并按照一定的比例(生存率)淘汰部分智能体.智能体适应度函数为:
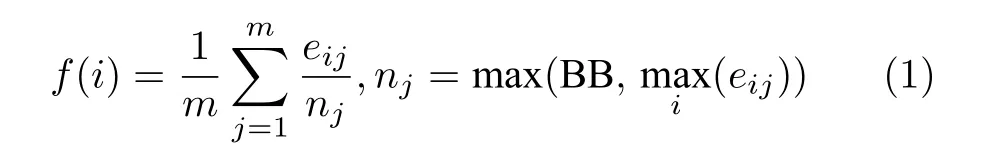
其中,f(i) 为智能体i的平均适应度,m为对手数量,eij为智能体i针对对手j的收益,nj为归一化因子,当智能体的最大收益小于一个大盲注(BB)时,将nj设置为大盲注以避免归一化错误.
b)交叉.交叉是为了将种群内的优势基因(策略网络参数)进行 “繁殖”得到下一代个体.为充分保留种群优势基因,本文将经过选择并生存的智能体进行分层,其中高于生存智能体平均适应度的部分个体将获得 “繁殖权”进行交叉,其余智能体则直接进入下一代种群中并再次进行评估和选择.这种分层方法在有效保留优势基因的同时,能够充分排除游戏随机性因素对智能体性能的影响.按照适应度对具有 “繁殖权”的智能体进行排序,适应度较高的智能体分别与每个适应度较低的智能体 “配对”,“配对”双方进行基因交叉过程,从而不断得到子代智能体基因,直到种群恢复至原始规模.
进一步,提取出 “配对”智能体的策略网络参数并分别将其拼接成参数向量作为交叉的2 种父代基因.基因交叉过程如图5 所示.对于图中2 组父代基因,将其分割成基因片段并按照其所属位置对双方的每组基因片段都按照智能体的适应度比例f(1)和f(2)进行随机选择,最终将所选择的基因片段组合成为新的交叉基因.
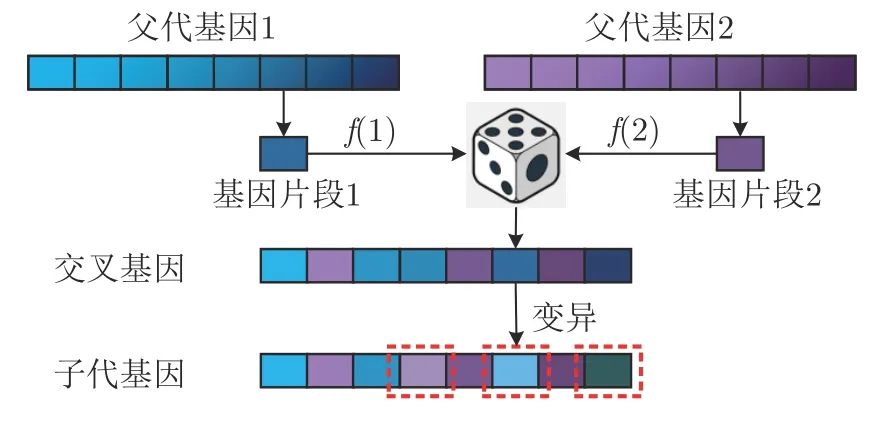
图5 智能体基因交叉变异示意图Fig.5 Crossover and mutation
c)变异.变异为子代基因增加了一定的随机性,从而提高对种群整体适应度的探索能力.变异过程遵循高斯分布,并且随着种群演化的进行,突变率和突变强度(即高斯分布的均值和标准差)线性下降.具体操作步骤是,首先按照突变率对图5中交叉基因的基因片段进行随机选择,所选中基因片段将加上服从该突变率和突变强度的高斯噪声从而得到子代基因,进而最终获得下一代种群.
上述步骤在训练过程中反复进行.随着不断地种群演化迭代,种群的整体适应度将不断提升,最终保存最后一代种群中适应度最高的基因作为智能体策略网络的参数.算法详细流程如算法1 所示.
4)对手特征库构建
为了在线博弈阶段实现对手博弈风格的度量识别,需要对不同对手的历史交互信息进行收集,从而构建对手特征库.对未知对手的博弈风格进行度量时,对手特征库主要用作比对的 “模板”.为此,本文使用训练得到的各类克制策略网络重新构建智能体,并分别与所克制的对手再次进行博弈交互,最终分别保留其特征提取器构建对手特征库.
2.2 在线博弈阶段
本阶段设计了一种对种群策略加权集成的博弈求解框架.该框架在对未知对手的博弈风格度量后,能够根据对手的博弈风格及时调整自身的集成策略,并且在建模置信度较低时,智能体也能使用基础策略网络的输出作为安全策略,从而避免智能体出现重大决策失误.该框架主要分为以下2 个模块:
1)对手博弈风格度量模块
本模块通过对未知风格对手与对手特征库中已知风格对手的博弈风格特征进行相似度度量,从而估计未知风格对手的博弈类型相似度.该模块具体结构如图6 所示.
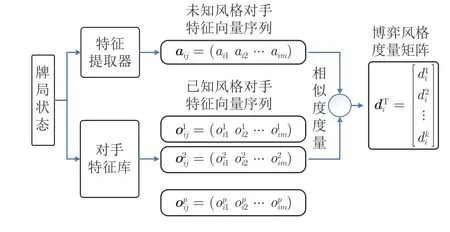
图6 对手博弈风格度量模块Fig.6 Measurement module of opponent's style
算法1.种群遗传算法


具体地,智能体与未知风格对手博弈过程中不断收集历史交互信息并构建特征提取器,从而逐渐提高对手建模可信度.在当前牌局状态对应的对手博弈风格特征达到置信度要求后,智能体将收集本游戏阶段内历史轨迹上所有结点的对手博弈风格特征向量序列,并与对手特征库中不同的已知风格对手的特征向量序列进行 “距离”度量,从而得到未知风格对手与已知风格对手的博弈风格度量矩阵:,(i=1,2,···,8;p=1,2,···,k).其中,k表示已知风格对手的数量,i表示智能体分别位于8 种不同游戏阶段(i=1,2,3,4 分别表示小盲位的4 个游戏押注阶段,i=5,6,7,8 则表示大盲位的4 个游戏阶段),表示未知风格对手在游戏阶段i与已知风格对手p之间博弈风格特征向量的相似度.相似度度量函数为:
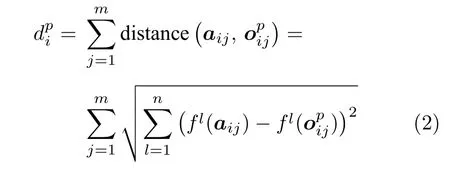
其中,m表示当前牌局状态对应游戏历史轨迹上的结点数量(即对手博弈风格特征向量数量),aij表示未知风格对手在游戏阶段i的第j组博弈风格特征向量,表示已知风格对手p的对应博弈风格特征向量,n表示特征向量维度,fl(aij)表示未知风格对手特征向量aij的第l种特征,fl()表示已知风格对手p对应特征向量的第l种特征.
2)克制策略集成模块
受到集成学习思想的启发,本节设计了如图7所示的种群策略集成模块,该模块中各个策略网络的输出是能够剥削不同风格类型对手的策略,而这些策略只是整个策略空间的一些局部最优解,因此在面对未知对手时并不具备适用性.本文设计的策略集成方法可以将不同克制策略网络的输出通过博弈风格度量矩阵D进行加权集成,从而构建集成策略πint.策略加权集成方式:

图7 种群策略集成模块Fig.7 Integration module of population strategies
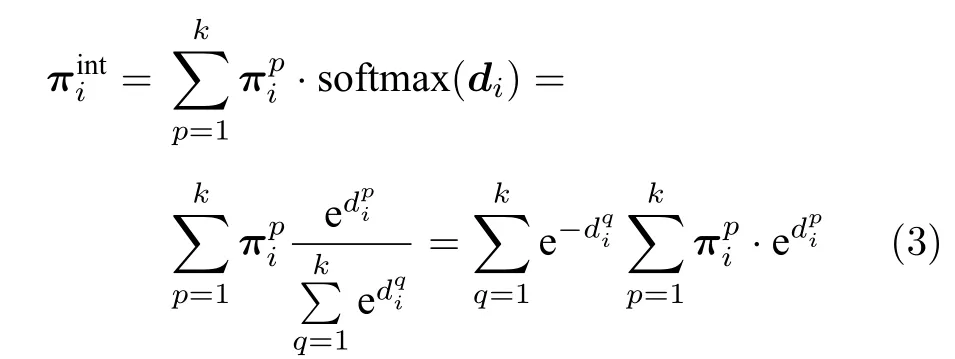
在与未知风格对手博弈交互的初始阶段,由于对手的特征收集累积量较少,因此对手建模的置信度较差,此外对于从未经历或者经历次数较少的牌局状态也会出现该问题.为避免因上述问题而导致决策失误,本节训练得到一个基础策略网络,该策略网络是由智能体与对手池中所有已知风格对手对打和种群演化训练得到的,其输出作为在对手建模置信度较低情况下的安全策略,从而保证智能体博弈性能的 “下限”.
3 实验与结果分析
3.1 实验设置
1)游戏参数设置与性能评价方式
本文所有实验均在2 人无限注德州扑克游戏环境中进行.其中,玩家每局总筹码量为 2×104,小盲注和大盲注分为50 和100,每局游戏结束后筹码重置并且双方交换位置.为评判智能体策略好坏,游戏双方对打 2×104局游戏并使用德州扑克AI 研究领域最为常见的平均每局千分之一个大盲注(Millesimal big blind per hand,mbb/h)作为智能体博弈性能的评价指标.
2)特征定义及编码
本文收集了10 种特征作为策略网络的输入,具体的名称、含义及编码方式如下:
a)访问频率:游戏历史中访问特征提取器中结点的频率,代表玩家在不同牌局状态下所有动作的频率分布信息;
b)弃牌率:特征提取器中当前结点为根的子树上因对手弃牌使游戏结束的频率;
c)摊牌率:特征提取器中当前结点为根的子树上双方玩家均未弃牌而使游戏进入摊牌阶段的频率;
d)期望牌力:特征提取器中当前结点为根的子树上摊牌时对手的平均牌力;
e)同花或顺子:当前公共牌对手同花或顺子的概率;
f)对牌数量:当前公共牌中对牌的数量;
g)游戏轮次:当前游戏所处轮次;
h)手牌牌力:自身当前手牌期望牌力;
i)对手加注额:对手加注的总筹码比例;
j)自身加注额:自身加注的总筹码比例.
其中,前4 种特征由特征提取器直接获得并组成得到对手特征向量,特征向量(例如:[0.143 2,0.483 3,0.652 8,0.118 9])中每一维度分别对应表示:访问频率、弃牌率、摊牌率和期望牌力.而游戏特征则由上述其余6 种特征对应组成,表示当前游戏公共信息和智能体私有信息.
对于对手博弈风格度量模块,本文需要获取特征提取器中本阶段游戏所对应的历史路径.对于其中每个结点本文设计了11 种对手博弈风格特征fl(aij)(l=1,2,···,11) 组成对应的特征向量aij,除了上述所列举的摊牌率和期望牌力,还包括当前牌局状态对手选择弃牌、跟牌/过牌、加注动作的概率(即特征提取器在当前牌局状态对应结点下每条边的访问频率),由于加注动作被抽象为7 种,因此特征提取器每个结点上都将得到一个11 维的特征向量aij.
3)对手设置
为给智能体策略网络种群演化训练提供对手,本文从图4 对手池策略空间中采样得到8 种具有已知风格的对手智能体 (O1,O2,···,O8),每种对手智能体的博弈风格及详细定义如表1 所示.表1 中前4 个对手 (O1,O2,O3,O4)是4 种风格最为明显的智能体,策略较为简单因而具有较高的利用率,在种群演化训练过程中比较容易被剥削.而表1 中后4 个对手 (O5,O6,O7,O8)策略相对复杂且利用率适中,有利于在种群演化训练过程中提高智能体策略的博弈水平.
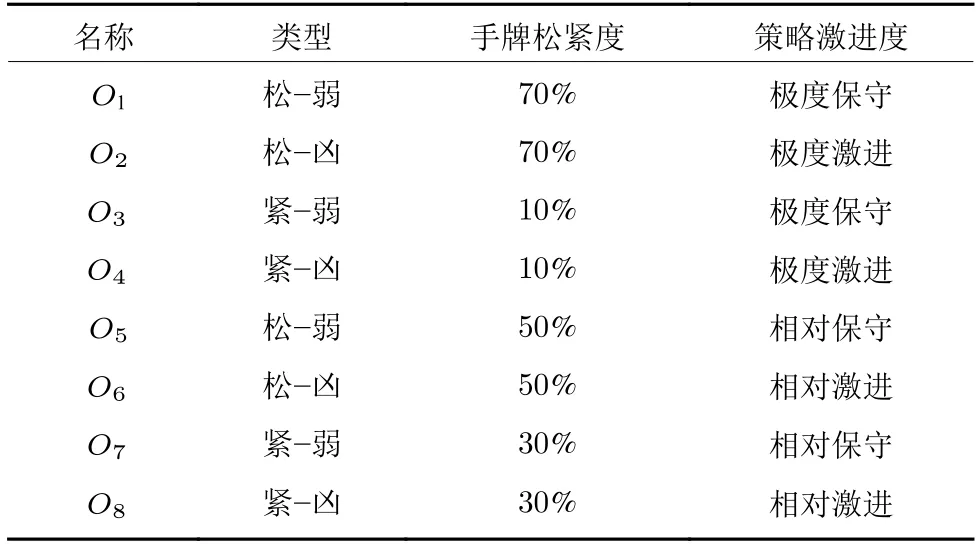
表1 对手智能体博弈风格及定义Table 1 The opponents'play styles and definitions
为验证智能体在对手策略不断变化时的适应能力,本文设计了一个可以进行策略动态切换的对手智能体Orandom,该智能体从对手池策略空间中每隔500 局游戏随机采样一种对手策略作为自身策略.
4)实验参数设置
表2 为策略网络结构和遗传算法训练的相关参数,表2 中数据是经过对算法训练的收敛速度和最终平均适应度水平综合考虑后确定的,各类策略网络均是使用表中所设置参数值进行种群演化训练得到.

表2 策略网络结构与训练参数Table 2 Policy network structure and the training hyper-parameters
基础策略网络通过种群智能体与定义的8 种对手交互训练得到,训练过程中对种群的100 个智能体进行300 代演化训练.每个智能体与单个对手每次对打 104种牌局,并对牌局进行手牌交换后重新对打,从而排除牌局随机性对性能的影响.因此,种群中每一个智能体均与每个对手对打 2×104局游戏后进行适应性评估和选择过程.最终第300 代种群中适应度最高的智能体策略网络保存为基础策略网络.
克制策略网络是通过智能体只与一种已知风格对手进行种群演化训练得到的,训练过程中也对种群的100 个智能体进行了300 代的种群演化训练,然后保存第300 代中适应度最高的智能体策略网络作为一种克制策略网络.因此对于对手池中定义的8 种不同风格对手,最终得到8 个能够分别克制对应对手的策略网络.
为构建对手特征库,首先利用每种克制策略网络重新构建智能体,然后与其克制对手对打 105局游戏,最后将特征提取器分别保存并构建对手特征库.
表2 中策略输出网络隐含层神经元数量和种群生存率2 种参数对算法的稳定性和收敛水平具有较大影响,为确定上述两种参数的合适取值,本文在基础策略网络训练过程中分别对2 种参数进行了网格搜索,参数对比结果见图8 和图9.
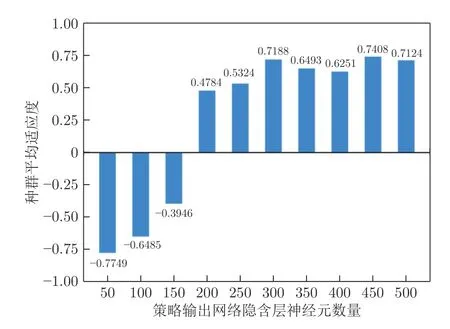
图8 策略输出网络隐含层神经元数量对种群平均适应度的影响Fig.8 The influence of the hidden neurons in policy output network on population fitness

图9 种群生存率对种群平均适应度的影响Fig.9 The influence of population survival rates on population average fitness
从图8 中数据对比可知,策略输出网络隐含层神经元数量的取值会对种群会的平均适应度收敛水平造成一定影响.神经元数目在50 到300 之间取值过程中,随着神经数量的增加适应度水平也在不断提升.当神经元数量达到一定数量后(即300 左右及以上),适应度水平并不会随之一直提升,而是最终达到一定的水平并趋于稳定.从图9 可明显看出,种群生存率对平均适应度的影响出现与图8 类似的变化趋势.说明当所选的参数值超过一定 “阈值”之后,系统性能的收敛水平对参数变化并不敏感.因而,在保证算法收敛水平的前提下尽量使用较少的参数量,根据网格搜索的结果最终分别将上述2 种参数设置为300 和0.25.
3.2 消融实验
1)基础策略网络训练
基础策略网络演化训练时智能体一直与多个对手博弈交互,由于对手具有不同的博弈风格和水平,因此训练过程中与不同对手的交互先后顺序可能会对种群的整体适应度产生较大影响.为最大化种群适应度,本文设计了一种三阶段的训练策略并与其他三种进行对比实验,得到如图10 所示的种群平均适应度变化曲线,其中:训练策略1 中智能体种群在300 代的演化训练时一直同时与表1 中的8 种对手交互;训练策略2 中智能体种群在前100 代演化训练中一直与前4 种对手交互,后200 代则只与后4 种对手交互;训练策略3 中智能体种群在前100 代演化训练中一直与前4 种对手交互,后200代则与8 种对手交互;训练策略4 中智能体种群在前100 代训练中一直与前4 种对手交互,中间100代只与后4 种对手交互,最后100 代则同时与8 种对手交互.
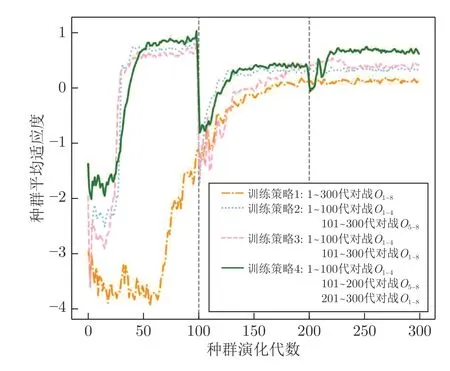
图10 不同训练策略对种群平均适应度的影响Fig.10 The influence of different training strategies on population average fitness
训练策略1 中智能体需要一直同时面对8 种不同风格对手进行对打训练,经过190 代左右的种群演化训练,其平均适应度最终收敛在0.1212 左右.该训练策略在训练过程中与另外两种训练策略相比表现出更大的 “震荡”幅度,而且需要更多的演化代数才能使种群的平均适应度提升并趋于平稳.
训练策略2 采用二阶段的分层训练方法,第1阶段中种群在第30 代左右平均适应度得到快速提升并收敛稳定在0.8515 左右;在第2 阶段中,由于所面对的对手利用率较低,因此种群在第101 代时的策略无法有效剥削此类对手,使其平均适应度也迅速降低至-1.5645.经过第2 阶段的训练,种群在第130 代左右平均适应度最终稳定到0.3312 左右.该训练策略 虽然与训练策略1 相比能够明显提高种群平均适应度收敛速度,但最终的平均适应度却明显低于训练策略4.这表明每次只面对其中4 种对手的分层训练策略可能会使种群在第2 阶段的训练后陷入局部最优,从而失去对前四种对手的克制性.
训练策略3 也采用两阶段的分层训练方法,是在策略2 的基础上更改第2 阶段所面对的对手得到,即后200 代同时面对8 种对手.从曲线对比来看,策略3 最终收敛水平与策略2 并无太大差异,但值得注意的是策略3 在第2 阶段训练开始时的震荡幅度明显强于策略2,训练过程中收敛速度和稳定性明显低于策略2.此外,策略3 与策略4 相比最终并不能达到相近适应度水平.
训练策略4 采用三阶段的演化训练方案,在前200 代的种群演化训练过程中其与策略2 的曲线变化趋势相似,种群的平均适应度最终稳定在0.665 4左右,与另外两种策略相比最终适应度得到较大提升.这表明训练策略4 的三阶段分层训练方式使种群具有较快的收敛速度并且避免陷入局部最优问题,最大化地探索了种群的博弈性能.
由图10 可以看出,训练策略4 能使种群平均适应度较快地收敛到更高的水平,因此本文将其作为基础策略网络的种群演化训练策略.
2)在线博弈阶段消融实验
为验证在线博弈阶段种群策略集成框架中不同模块的作用,本节对其进行消融实验,结果见表3,其中Slumbot1http://www.slumbot.com/是世界计算机扑克大赛中2 人无限注德州扑克组冠军智能体,代表纳什均衡策略智能体,并作为本实验对照组,表3 中每组实验数据均表示不同智能体面对某种对手时的评估性能,例如智能体Abase与对手O1的评估结果是1 000 mbb/h,表示经过 2×104局游戏的对打评测后,结果表明Abase博弈性能优于O1.
Atar为克制策略智能体,其构建分别使用了不同的克制策略网络,主要用于分别评估每种克制策略网络对其所克制对手的剥削性能.因此,表3 中第1 行评测数据均是某种对手与对应克制策略智能体的评估结果,比如第1 行中第1 组数据代表对手O1的克制策略博弈性能为999.92 mbb/h.由测评数据可以看出,各克制策略均能有效克制对应类型的对手.由于克制策略只能针对一种对手,所以此类评测数据可视为本文提出的种群策略集成框架智能体在面对对手池中已知对手时的性能 “上界”.
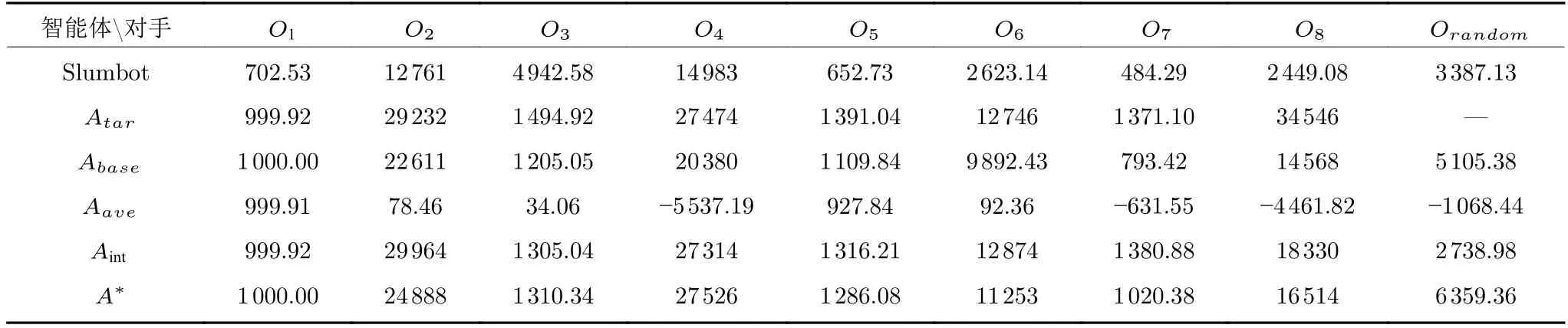
表3 消融实验结果(mbb/h)Table 3 Ablation study results (mbb/h)
Abase为基础策略智能体,其构建只使用基础策略网络,用于单独评估基础策略网络的性能.测试数据表明Abase在单独面对已知的不同对手时均具有相对良好的博弈性能,这验证了基础策略网络所采用的三阶段分层种群演化训练方式,既能保证种群博弈性能得到快速提升,又能避免因为不同训练阶段面对不同对手所造成的克制策略 “遗忘”问题.此外,Abase与动态策略对手Orandom的评测结果为5 105.38 mbb/h,这说明即使对手策略变化时基础策略也具有一定的适应性,所以基础策略网络的输出可以作为建模置信度较低时的安全策略.
Aave为克制策略网络静态集成的智能体,其策略是直接将各个克制策略网络的输出进行 “加和”得到的(即博弈风格度量矩阵为均匀分布),主要用于探究在没有安全策略和对手博弈风格度量矩阵的情况下直接进行策略集成时智能体的性能表现.从Aave、Atar及Abase的实验结果对比可以看出,这种直接对局部最优解 “加和”的集成方法,失去了克制策略原有的剥削性能,使智能体即使在面对已知对手时也无法保证其博弈性能.此外,Aave与动态策略对手Orandom的评测结果为-1 068.44 mbb/h,说明在面对对手变化时,Aave由于没有对手相似度的度量模块,导致其不具有对动态策略的适应性.
Aint为没有基础策略作为安全策略的动态集成策略智能体(即在Aave的基础上加入对手博弈风格度量模块),用于评价在只使用对手博弈风格度量并进行策略集成时智能体的性能表现.通过Aint与Aave的实验数据对比可以发现,在使用博弈风格度量矩阵将克制策略进行加权集成后,Aint的博弈性能相比Aave得到显著提升,这说明Aint的集成策略保留了各克制策略的剥削性能.在面对策略随机变化的对手Orandom时,Aint的测评结果明显低于其在面对8 种已知对手时的平均性能,这说明在对手策略变化时,Aint由于由于没有基础策略作为安全性保障,因此容易因建模置信度低而造成决策失误.
A*为本文提出的种群策略集成框架所对应的智能体.相比于智能体Aint,A*虽然在面对已知对手时性能表现略低于Aint,但是因其拥有基础策略网络模块作为安全策略,使得在面对动态策略对手Orandom时A*的性能均明显优于Aint和Abase,这体现基础策略网络可以有效减缓可能出现的决策失误问题.此外,从分别面对Orandom时的评测结果来看,A*的性能为6 359.36 mbb/h,明显高于Slumbot 对应的3 387.13 mbb/h,这说明即使在面对对手策略变化时A*相比传统的纳什均衡策略也能够更好地剥削对手,保证自身能够有良好的博弈性能.
3.3 性能对比
1)算法博弈性能
为评估智能体A*的实际博弈性能,本节将其与第1.2 节所述4 种方法、知识AI 和Orandom分别对打测评,结果见表4,其中知识AI 是5 种基于人类专业玩家策略的规则智能体,该类智能体具有动态的策略和完备的人类常见打法,可以模拟人类玩家行为,表格中知识AI 的评测数据均是与五种人类规则AI 对打 2×104局游戏后的平均结果.
从表4 可以看出,智能体A*、ASHE、NFSP 和知识AI 分别在面对目前具有最强性能的Slumbot 和DeepStack 时,评测统计结果说明这种利用CFR 算法求解的近似纳什均衡策略极难被剥削.智能体A*在面对知识AI 时评测统计结果达到229.64 mbb/h,与ASHE 和Slumbot 分别对应的-13 mbb/h 和52.43 mbb/h 相比得到大幅度性能提升,另外在面对Orandom时智能体A*同样具有最好的性能表现.

表4 博弈性能对比结果(mbb/h)Table 4 Performance comparison results (mbb/h)
为评估不同方法智能体在博弈过程中策略的动态变化情况,本文记录了智能体A*、ASHE、Slumbot 和DeepStack 分别与Orandom测评过程中的收益变化情况,博弈性能变化曲线如图11 所示.数据从第5 000 局游戏开始,每隔500 局游戏统计一次前5 000 局的平均博弈性能得到的.可以看出,Slumbot 和DeepStack 这种典型的纳什均衡策略智能体,在面对动态策略对手Orandom时由于策略的静态性使其不具备动态适应性.智能体A*和ASHE 能够不断收集交互数据从而建模对手,使其均具有一定的适应能力,但由于智能体A*能够通过策略集成策略框架来根据对手实际风格特征针对性地适应对手,使其相对ASHE 具有更加强大的动态适应性.
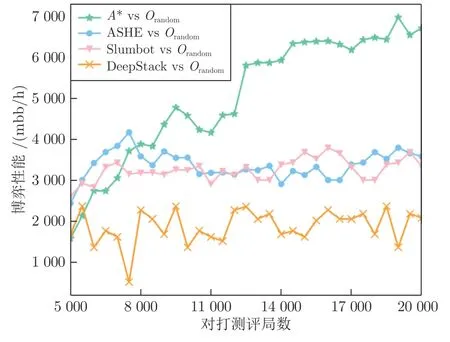
图11 对打测评过程中博弈性能变化Fig.11 The change of game performance in the evaluation process
上述实验可以有效说明,本文所提出的博弈求解框架,在博弈交互过程中可以不断建模对手从而获得一定的适应性,并相比已有方法能够大幅提升面对不断变化的对手策略时的博弈性能.实验结果也验证纳什均衡策略所存在的严重限制智能体剥削性问题,使其在对手策略变化时无法最大化自身收益.
2)算法轻量性
为评估本文所提出博弈求解框架的轻量性,本节对比不同算法分别在训练和测评2 个阶段的资源需求,包括存储资源需求、计算资源需求以及测评的动作响应时间.详细对比数据如表5 所示,表5数据均来自原始论文以及复现时的实际数据.
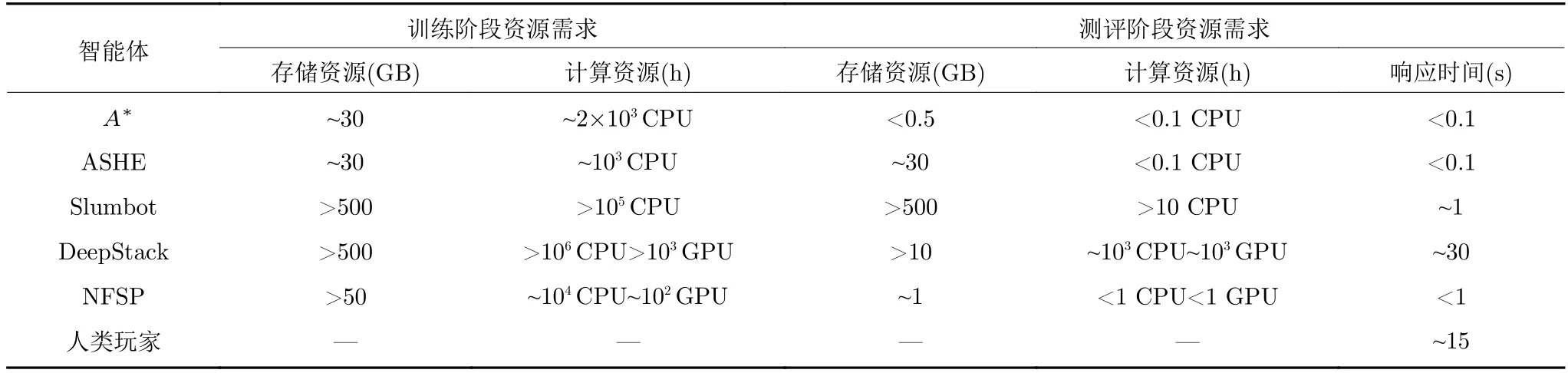
表5 算法轻量性对比Table 5 Light-weight comparison
对于训练阶段,从存储资源需求来看,Slumbot 和DeepStack 由于需要使用CFR 相关算法求解并保存纳什均衡策略,因此需要500 GB 以上的存储资源,NFSP 则需要50 GB 以上的内存资源将不断采样到的交互数据保存到经验回放池,而智能体A*和ASHE 仅需要约30 GB 的存储资源来离线保存牌力数据.从算法计算资源需求来看,智能体A*略高于ASHE 的计算资源需求(小于2 倍),仅需一台无GPU 的常规计算机使用约2000 个CPU小时的计算量,远低于Slumbot、DeepStack 和NFSP 这种需要大规模计算机集群进行分布式计算求解的智能体.在对打测评阶段,智能体A*对每一局游戏的实际牌力进行在线解算,在不牺牲响应速度的前提下有效降低对存储资源的需求,使其对存储和计算资源的需求量均小于其他智能体.最终,智能体A*能够以平均小于0.1 秒的动作响应时间进行博弈交互,远低于DeepStack 和人类玩家.
综上所述,本文提出的博弈求解框架能够在较少计算和存储资源的情况下保证自身博弈性能和响应速度,相比其他已知求解方法更具有轻量性优势.
4 结论
本文提出了一种针对两人无限注德州扑克这种典型大规模不完美信息博弈问题的博弈求解框架,具有轻量高效并能快速识别和适应对手策略变化等优点.该框架首先基于演化学习方法对智能体进行种群演化训练得到剥削不同风格对手的克制策略网络,然后对未知风格对手进行在线建模和风格度量,最后采用种群策略集成最大化剥削和利用对手.
针对基础策略网络的种群演化训练过程,本文探讨了4 种不同的训练策略对种群平均适应度的影响.通过对比,本文的三阶段分层训练方式能有效提升训练速度和种群平均适应度.在线博弈阶段的消融实验中,本文验证了不同模块的作用.实验数据表明,本文提出的种群策略集成框架能有效度量未知对手的博弈风格,并调整自身集成策略来提升收益.由评测结果可得,本博弈求解框架智能体A*在分别面对动态策略的对手Orandom和人类规则的知识AI 时,其博弈性能明显强于基于纳什均衡策略的智能体.这说明相比纳什均衡策略,即使对手策略发生变化A*也能够更好地剥削对手,保证自身良好的博弈性能.综上所述,本文提出的不完美信息博弈求解框架能够有效建模未知对手并度量其所属风格,利用克制策略的加权集成与对手交互,有效提高智能体在面对不同对手时的剥削性能.
本文提出的博弈求解框架具有一定的通用性,该框架不仅适用于德州扑克这一特定游戏环境,还可以为实际生活中的诸多不完美信息博弈问题提供一种可行的解决思路.未来值得进一步探索的问题包括强化学习在本框架中的应用方式以及本框架在多人德州扑克游戏中的拓展问题等.
