数据驱动的保证收敛速率最优输出调节

姜 艺 范家璐 柴天佑

在实际的控制器设计问题中,通常是希望将被控对象的输出跟踪给定的设定值或给定的期望轨迹,即实现输出跟踪.对于前者,PID 控制器[1]、模型预测控制器[2]是一类经典的解决方案.对于后者,该问题通常可以建立成一类输出调节问题[3-6],该问题的目标通常包括两部分,设计稳定的控制器使得输出信号与给定参考轨迹的误差是渐近稳定的,并且能够完全可以克服外部系统所产生扰动信号对系统所产生的影响.然而,解决输出调节问题通常依赖于已知的精确模型参数,而在一些特殊情况下该要求是难以满足的.

针对模型未知的被控对象的输出跟踪问题,一些专家学者提出了基于自适应的控制方法,如模型参考自适应控制[7]、无模型自适应控制[8]、神经网络自适应控制[9],这些方法可以在部分模型知识未知的情况下,很好的实现输出跟踪.而在有些情况下,控制器目标需要使得最小化给定的性能指标,同时希望系统的动态性能满足一定要求,这使得需要设计最优自适应控制器.

为解决最小化给定的性能指标问题,一些专家学者提出了基于强化学习的自适应控制方法,该方法通过与未知被控对象的交互来更新控制策略,使得控制器是最优的.对于跟踪问题,主要有两类基于强化学习的方法,一类是将跟踪问题定义为一类最优二次型跟踪问题,另一类是基于输出调节理论的最优输出调节问题.利用前一类方法,文献[10-11]与文献[12-15]分别解决了连续与离散线性系统的最优跟踪控制问题,文献[16]与文献[17-19]分别解决了连续与离散非线性系统的最优跟踪控制问题.利用后一类方法,文献[20-23]与文献[24-26]分别解决了连续与离散线性系统的最优输出调节问题,文献[27]与文献[28]分别解决了连续与离散非线性系统的最优输出调节问题.上述方法是基于状态反馈与策略迭代的方法,而对于系统状态难以在线测量的系统,上述方法不能直接应用,针对这个问题,文献[29]与文献[30]分别设计了基于输出反馈的控制器解决了最优跟踪控制问题与最优输出调节问题.对于动态性能要求,文献[31]针对单无人机对单目标的环航跟踪问题,设计了飞行轨迹快速收敛到期望航迹的控制器.文献[32]通过设计状态反馈和动态输出反馈控制,研究了机器人系统的有限时间控制问题.然而,上述文献需要利用系统的动态模型参数来设计合适的Lyapunov 函数.

为了使系统的动态特性满足预先给定的要求,同时实现最优自适应控制,本文提出保证收敛速率的数据驱动线性离散系统最优输出调节方法,该方法不需要部分模型知识,与文献[24-25]中的方法与被控对象相比,该算法不需要稳定的初始控制律,同时输出方程中输入到输出的前馈增益矩阵不等于0,利用在线的状态数据、输入数据,或者在线的输出、输入数据求解得到基于状态反馈与输出反馈最优的输出调节器,并保证跟踪误差的收敛速率满足预先给定的要求.

本文结构如下:第1 节给出离散线性系统的最优输出调节问题描述,第2 节与第3 节分别进行基于状态反馈与输出反馈的自适应最优输出调节器设计,第4 节给出设计方法的收敛性与系统闭环稳定性分析,第5 节利用仿真实验验证本文设计方法的有效性,第6 节为结论.

1 控制问题描述

考虑如下受扰动的线性离散系统

传统的输出调节问题的控制器设计目标为使得跟踪误差e(k) 是渐近稳定的,即 l imk→∞e(k)=0.本文目标为利用外部系统数据w(k),系统输入u(k),系统状态x(k)或系统输出y(k)设计最优输出调节器,使得跟踪误差e(k)是渐近稳定的,同时期望跟踪误差e(k)的收敛速率快于γ-k,其中γ＞1.该问题可以定义为求解如下问题.

问题1.针对被控对象(1)～ (2),对应的外部系统为(3)～ (4),设计控制器u(k)使得跟踪误差满足

为解决该问题,根据输出调节理论[3,33],该问题的输出调节方程为

其中,X∈Rnx×nw与U∈Rnu×nw为输出调节方程的待求解未知数.利用Kronecker 积,输出调节方程(7)～ (8)可写为

基于假设2 可知,Γ 是行满秩的,输出调节方程(7)～ (8)是有解的[33].基于该解,并同时考虑控制器设计要求为使得跟踪误差e(k)的收敛速率快于γ-k,定义新系统为

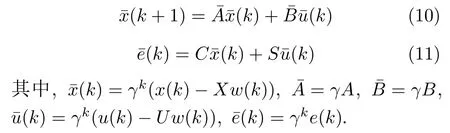
基于新系统(10)～ (11),建立如下最优控制问题与约束最优化问题.通过求解该问题,可以保证式(6)成立,即跟踪误差e(k)的收敛速率快于γ-k,该性质将会在闭环系统分析部分进行证明.

问题2[34].针对系统(10)～ (11),给定Q≥0,R ≥0,设计基于状态反馈与输出反馈的最优控制输入,使得如下性能指标最小

2 基于状态反馈的自适应最优输出调节器设计

本节在被控对象状态方程(1)中矩阵A、B、D、E未知、被控对象输出方程(2)中矩阵C、S与F已知的情况下,设计数据驱动的基于状态反馈的最优自适应输出调节器.首先给出基于状态反馈的最优输出调节器的解,之后利用该解的求解形式,设计数据驱动的基于值迭代的自适应最优输出调节器.值得注意的是,由于本节所设计的是基于状态反馈的最优输出调节器,因此需要利用状态计算跟踪误差,故矩阵C、S与F已知的假设是合理的.

2.1 基于状态反馈与模型的最优输出调节器

利用该式可以得到输出调节方程(7)～ (8)的解X和U.

以上为基于模型的输出调节方程(7)～ (8)的求解,与文献[32]直接求解输出调节方程不同,式(20)中的求解方法将会为第2.2 节中自适应控制器设计提供指导.

然而,直接求解Riccati 方程比较复杂,针对此问题,该小节利用基于值迭代的算法求解,其收敛性性质见如下引理.

算法1.基于模型的值迭代状态反馈最优输出调节算法

证明.文献[37]给出了当S=0 时的收敛性证明,本文将简述S0 时的收敛性证明.首先将式(28)与式(26)定义为

注3.对于基于策略迭代的算法[24-25,38],其初始控制律K0要求矩阵是稳定的,即A-BK0的特征值在以原点为圆心,半径为 1/γ的圆内,当矩阵A,B已知时,选择满足该条件的初始控制律K0是很容易的,然而,当矩阵A、B未知时,初始控制律的选择则更加严格.因此,本文使用基于值迭代的算法,该算法的初始控制律K0可以是任意的,同时该算法不用重复求解Lyapunov 函数[24-25,38].

以上为基于模型的问题求解方法,该求解方法将会为下一节中自适应控制器设计提供指导.

2.2 基于状态反馈与强化学习的自适应最优输出调节器

可将式(41)转化为如下方程组

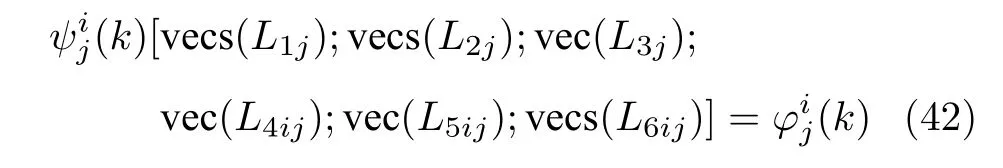
当在线数据满足一定要求时,上述方程组可由最小二乘方法求解.如下引理给出了方程组(42)具有唯一解的条件.

引理 2.方程组(42)可解并具有唯一解,当且仅当

当引理2 成立时,方程组可以由下式求解,为

同时考虑式(30)与式(31)可得

以上为反馈控制增益Kj的在线计算过程,该部分将介绍如何在线求解输出调节方程(7)～ (8)的解X和U,基于式(17)可得

利用上式,可将输出调节方程(7)～ (8)写为

其中

利用矩阵行变换,可以将式(47)重写为类似式(19)的形式,进而可以利用式(20)进行求解得到输出调节方程(7)～ (8)的解X和U,最后利用式(29)得到前馈增益.至此,基于状态反馈与强化学习的自适应最优输出调节算法如下.

算法2.基于状态反馈与强化学习的自适应最优输出调节算法

初始化:选择任意的初始控制律K0,终止条件常数ε＞0,半正定矩阵P0,矩阵序列Xi ∈Rnx×nw与Ui ∈Rnu×nw,j←0,i←0;

最优反馈控制律在线计算:利用如下迭代算法计算最优反馈增益,在区间 [k,k+s] 利用控制输入为u(k)=-K0x(k)+n(k),其中n(k)为控制输入中添加的探测噪声,s为使得引理2 满足的数;

1) 利用式(43) 计算得到L1j,L2j,L3j,L4ij,L5ij,L6ij;

2) 利用式(44)计算Pj+1;

3) 判断 ‖Pj+1-Pj‖＜ε是否成立,如果成立则停止迭代,并利用式(45)计算得到Kj,反之重复上述两步,并令j←j+1;

前馈增益在线计算:令i←i+1,重复计算得到所有L4ij直到i=m+1,进而利用式(24) 进行求解得到输出调节方程(7)～ (8)的解X和U,最后利用式(29)得到前馈增益.

注4.值得注意的是,中仅含有过程数据,因此,该值在迭代过程中对于固定i仅需要计算1 次,相较于基于策略迭代的方法,本文方法虽然迭代步数多,但每一步所需要的计算量却小一些.

注5.对于序列,由于并不参与过程迭代,Kj仅需要在Pj收敛后计算1 次.因此,在该算法过程中u(k)并不需要进行在线更新,因此该方法是一类离线策略,相较于在线策略,该方法可以保证计算结果是无偏的[39-40].

注6.探测噪声n(k)的加入是为了使得引理2的条件满足,达到充分激励的效果.通常选择为白噪声或者正弦函数等.

3 基于输出反馈的自适应最优输出调节器设计

本节在被控对象(1)～ (2)中矩阵A、B、D、S、E、C与F未知、在lU已知的情况下,设计基于输出反馈的最优自适应输出调节器,首先利用历史的输入输出数据设计重构状态[29-30,41],之后设计基于值迭代的输出反馈自适应最优输出调节器.

3.1 状态重构

3.2 基于输出反馈与强化学习的自适应最优输出调节器

由式(29) 可知,最优输出调节问题可由如下控制输入求解

上式的Riccati 方程难以直接求解,基于式(55)与动态方程

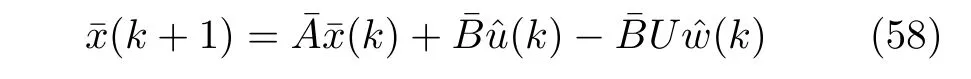
可得

可将式(59)转化为如下方程组

当在线数据满足一定要求时,上述方程组可由最小二乘方法求解.如下引理给出了方程组(60)具有唯一解的条件.

引理3.方程组(60)可解并具有唯一解,当且仅当

当引理3 成立时,方程组(60) 可以由下式求解,为

至此,基于输出反馈与强化学习的自适应最优输出调节算法如下.

算法3.基于输出反馈与强化学习的自适应最优输出调节算法

4 算法收敛性与闭环稳定性分析

本节进行所设计的状态反馈与输出反馈自适应最优输出调节算法的收敛性分析与基于所设计的最优输出调节器的闭环系统稳定性分析,如下两个定理分别给出了收敛性结论与稳定性结论.

5 仿真实验

本节进行所提算法的仿真实验研究,首先介绍仿真实验对象与实验参数,之后分别进行基于状态反馈的仿真实验与基于输出反馈的仿真实验.

5.1 仿真实验对象与实验参数

考虑如下受扰动的线性离散时间系统

5.2 基于状态反馈的仿真实验

探测噪声n(k)为白噪声,被控对象的初始状态为x(1)=[1 2]T与w(1)=[2 1]T.由引理2 可知,求解公式(42)至少需要15 组数据,故s需大于14,仿真实验中选择s=17.

仿真结果如图1～ 3 所示,图1 表示基于状态反馈的输出y(k)与参考信号yd(k)的轨迹,由该图可知本文所提方法能够在系统矩阵A,B,D,E未知时实现自适应输出调节,图2 表示基于状态反馈的 ‖Pj-P*‖与 ‖Kj-K*‖的误差轨迹,由图可知经过13 步迭代算法收敛,图3 表示基于状态反馈的误差e(k)与γ-ke(k0)的对比曲线,实验结果表明所设计的控制器能够使得跟踪误差收敛快于γ-k.

图1 基于状态反馈的输出y(k)与参考信号yd(k)轨迹Fig.1 Trajectories of the output y(k) and the reference signal yd(k) via state feedback

图2 基于状态反馈的 ‖Pj-P*‖与‖Kj-K*‖误差轨迹Fig.2 Trajectory of the error between ‖Pj-P*‖and‖Kj-K*‖via state feedback

图3 基于状态反馈的误差e(k)与 γ-k e(k0)对比曲线Fig.3 Comparison curve of e(k) and γ-k e(k0) via state feedback

5.3 基于输出反馈的仿真实验

本小节进行基于状态反馈的仿真实验,仿真实验中,初始控制律

终止条件常数ε=80,半正定矩阵P0=0,探测噪声n(k) 为白噪声,被控对象的初始状态为x(1)=[1 2]T与w(1)=[2 1]T.由引理3 可知,求解式(60)至少需要45 组数据,故s需大于44,仿真实验中选择s=64.

仿真结果如图4～ 6 所示,图4 表示基于s 输出反馈的输出y(k)与参考信号yd(k)的轨迹,由该图可知本文所提方法能够实现自适应输出调节,图5表示基于输出反馈的的误差轨迹,图6 表示基于输出反馈的误差e(k) 与γ-k e(k0)的对比曲线,实验结果表明所设计的控制器能够使得跟踪误差收敛快于γ-k.

图4 基于输出反馈的输出y(k)与参考信号yd(k)轨迹Fig.4 Trajectories of the output y(k) and the reference signal yd(k) via output feedback

图5 基于输出反馈的 ‖-‖与‖-‖误差轨迹Fig.5 Trajectory of the error between ‖-‖and‖-‖via output feedback

图6 基于输出反馈的误差e(k)与 γ-ke(k0)对比曲线Fig.6 Comparison curve of e(k) andγ-ke(k0)via outputfeedback

5.4 对比仿真实验

本小节进行对比仿真实验,其中对比方法选用文献[24] 方法,对比实验的参数选择为Q=1,R=30,收敛速率γ=3.由于文献[24]中的方法无法求解输出调节方程(7)～ (8)的解X和U,对比实验中求解X和U均使用本文的方法.对比方法中的初始控制策略为稳定的.对比仿真结果如图7表示,实验结果表明,与对比方法相比,在相同的权重矩阵参数下,本文所设计的控制器使得跟踪误差收敛快于γ-k,而对比方法计算得到的控制器使得跟踪误差收敛慢于γ-k.

图7 对比仿真结果Fig.7 Comparison of simulation results

6 结束语

本文针对具有未知动态与收敛速率要求的受扰离散线性系统的输出调节问题,提出了基于状态反馈与输出反馈的自适应最优输出调节算法,该算法不需要稳定的初始控制律与部分模型知识,利用在线算法求解得到最优的输出调节器,同时还能够保证跟踪误差的收敛速率满足预先给定的要求.本文的后续工作将着重于研究基于动态反馈的输出调节算法,以克服对部分模型知识的要求.