太沙基地基极限承载力系数的进一步讨论

程国勇，王兆源，刘大海

（1.中国民航大学交通科学与工程学院，天津 300300；2.深圳市地质局，广东 深圳 518023）

条形基础的太沙基地基极限承载力理论[1]是最具代表性和应用最广泛的地基承载力理论，其地基极限承载力计算通式为

式中：Nq、Nc、Nγ为地基承载力系数；q 为基础两侧外荷载；c 为土体粘聚力；γ 为地基土重度；B 为基础底面宽度。

文献[1-2]给出了基底完全光滑及完全粗糙情况下Nq和Nc的确切解析式如下

式中：ψ 为基础下刚性核两侧边与水平面夹角；φ 为摩擦角。 但其对于Nγ仅给出了含有待定系数的准解析式如下

式中kpγ为被动土压力系数，需经试算确定。

文献[3-8]给出了基底特定情况下Nγ的经验公式或基于经验公式的数值表。在基底完全光滑条件下（ψ=π/4+φ/2），常见的经验公式如下

在基底完全粗糙条件下（ψ=φ），常见的经验公式不仅包括式（5），还有其他经验公式如下

从式（5）～式（8）可以看出，以上这些经验公式差别较大且相互间可能存在矛盾，对公式的来历、考虑因素等缺乏系统的阐述而难以深究。 这种状况给地基承载力理论的学习及应用带来不少困惑。 文献[9-10]对Nγ的确切表达式进行了研究，并给出了基底完全粗糙条件下Nγ的解析解和基底一般粗糙条件下的完整解析解如下

但经进一步的严格理论分析发现，式（9）及式（10）在推导过程中存在疏漏。

根据上述分析，基于极限平衡原理对太沙基地基极限承载力这一经典问题重新进行了严格理论分析，对以往研究的不足进行了纠正并与相关文献资料进行了对比，进一步促进太沙基地基极限承载力理论的学习和应用，并为相关研究工作提供参考或借鉴。

1 地基极限承载力的理论分析

1.1 参数说明

参数说明如表1 所示。

表1 参数说明Tab.1 List of parameters

1.2 原理

本研究仍采用太沙基地基极限承载力理论的3条假定[1-2]：

（1）基础底面粗糙，刚性核与两侧面与水平面夹角为ψ；

（2）不考虑基底以上基础两侧土体抗剪强度影响，仅将其看作均布荷载；

（3）地基中滑动土体分为三角形压密区（刚性核）、朗肯被动区以及对数螺旋线过渡区。

太沙基理论计算图示如图1 所示。

图1 太沙基理论计算图示Fig.1 Calculation scheme of Terzaghi’s formulas

从图1 中可看出，当地基发生破坏时，土体沿bde和bd′e′滑动，和是对数螺旋曲线，de 和d′e′是直线，与水平面的夹角等于，即ade 及a′d′e′区为朗肯被动区。 从图1 中可得到三角形压密区（刚性核）aa′b 与对数螺旋曲线过渡区a′bd′之间分界线段a′b 长度，计算公式如下

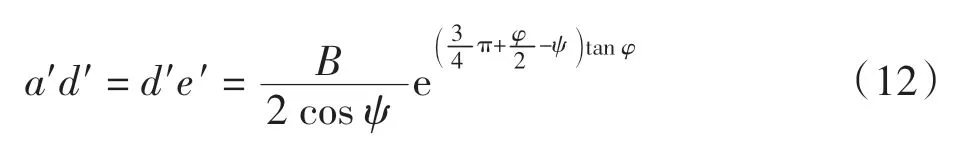
取aa′b 为隔离体，受力分析如图2 所示。

图2 刚性核受力分析Fig.2 Analysis of rigid core force

根据几何条件可知Ep与竖直方向夹角为ψ-φ，根据静力平衡条件可得

从式（13）可以看出，只要求出了Ep，则地基的极限承载力就可确定。

1.3 刚性核侧面被动土压力Ep 的求解

从上述分析可知， 地基极限承载力qu求解的关键在于首先要求得Ep。为便于求解，取a′bd′e′为隔离体， 并分解为以下3 种情况分别求解Ep的反作用力及

仅考虑地基土自重情况下（即q=0、c=0、γ ＞0），隔离体a′bd′e′受力情况如图3 所示。

图3 重力引起的被动土压力Fig.3 Passive earth pressure caused by gravity

从图3 中可看出，G1、G2分别为朗肯被动区a′d′e′及对数螺旋线过渡区a′d′b 的重力；滑动面上反力分布为三角形且分别与各自的法线夹角为φ。分别求隔离体a′bd′e′所受外力对于a′的力矩（以顺时针为正）。

1）G1对于a′点力矩Mγ1（顺时针）

G1对于a′点力矩Mγ1（顺时针）可表示为

式中G1可表示为

2）G2对于a′点力矩Mγ2（逆时针）

G2对于a′点力矩Mγ2（逆时针）可表示为

式中Rr可表示为

仅考虑基础两侧外荷载作用（即q ＞0、c ＞0、γ ＞0）情况下，隔离体a′bd′e′受力情况，如图4 所示。

图4 外荷载引起的被动土压力Fig.4 Passive earth pressure caused by load

式中

2）外荷载q 对a′点的力矩Mq2（顺时针）

Mq2可表示为

仅考虑土体粘聚力c 时（即q=0、c ＞0、γ=0）情况下，隔离体a′bd′e′受力情况如图5 所示。

图5 粘聚力引起的被动土压力Fig.5 Passive earth pressure caused by cohesion

滑动面上土体粘聚力c 对于a′点的力矩（顺时针）表示为

1.3.4 被动土压力汇总

上述3 种情况分别求得的被动土压力进行叠加，即

1.4 地基承载力系数的计算

根据刚性核的受力分析，将式（33）代入式（13）并整理可得

根据式（1）可得Nq、Nc、Nγ3 个承载力系数。

1.5 对比分析

从上述分析过程可以看出，依据太沙基地基极限承载力理论最初的假设及计算模型，经严格理论推导可得到3 个承载力系数的确切表达式。 其中：Nγ与当前文献研究均不同， 而Nq和Nc两个系数的表达式和相互关系表述与所有土力学教材或文献完全一致。

将本研究所得Nγ与当前文献经验公式或数值进行列表对比，如表2 所示。

表2 文中Nγ 公式与当前文献经验公式或数值对比Tab.2 Comparsion of the Nγ formula in this thesis with empirical formulas or statistics in cited works

2 结语

本研究从太沙基地基承载力这一经典课题出发，通过数学推导的方法得出3 个地基承载力系数的解析解，拓宽了原有理论的适用范围，提出结论如下。

（1）从太沙基地基极限承载力理论基本假设及计算模型出发，经严格力学分析可得到承载力系数Nγ的确切表达式而不必附加其他条件，例如待定系数、试算等。 对此问题的澄清不仅对太沙基地基极限承载力理论的完备有学术价值，对地基极限承载力理论的学习、工程应用及学术研究也有参考价值。

（2）在以前类似研究的基础上重新推导得到Nγ的表达式，纠正了以前研究过程中的漏项及笔误，并通过了反复校核。 基于相同假定及计算模型同步推导得出的另外两个承载力系数Nq和Nc与当前所有土力学教材或文献完全一致，也从侧面间接印证了所求Nγ表达式的正确性。

（3）由于基本假定及计算模型等方面与实际情况的差异，理论推导得到的Nγ未必能直接用于工程实践，需要利用实测数据进行修正，与此问题的理论探究并不冲突。将文中Nγ表达式与其他经验公式或数值表进行列表展示也仅为便于应用和理解，相互之间并不能相互验证或纠正。