一种融合优化选择策略的差分粒子群算法

张德华，郝昕源，张妮娜，魏 倩，刘 英

(1.河南大学 计算机与信息工程学院，河南 开封 475004；2.武警综保中心运维室，陕西 西安 711700)

在分布式多传感器多目标数据融合系统中，传感器系统偏差配准的目标是准确估计并校正传感器的固有系统偏差，为其后续的信息融合以及数据处理提供技术保障，其偏差配准质量将直接影响多传感器多目标数据信息融合系统的性能与可靠性。

传统的系统偏差配准算法有：① 基于最小二乘配准算法，这种算法忽略了测量误差，把误差完全归于系统误差，且计算量也会随着数据增多而剧增[1]；② 基于极大似然算法，该算法只解决了二维模型，采用地球投影，存在模型不准确的问题[2]。为了解决此问题，KARNIELY等[3]提出了用神经网络算法进行系统偏差配准，由于采用梯度下降算法，存在收敛速度慢、易陷入局部最小值以及出现“锯齿”现象等问题[4-6]。研究者不断探索新的有效的网络训练方法，有研究者提出了用粒子群算法(Partide Swarm Optimization，PSO)与网络相结合的算法，但粒子群算法本身又存在进化后期种群多样性缺失的问题[7-8]。为了克服这个问题，有人提出将差分进化算法与粒子群算法(Differential Evolution Particle Swarm Optimization，PSO-DE)相结合[9-14]，但此方法在两个种群全局最优适应度值相差较小时，会出现不必要的信息交流误差。

针对上述问题，笔者提出了一种融合优化选择策略的差分粒子群算法(Optimal Selection Particle Swarm Optimization-Differential Evolution-Weigthed Networks，OSPSO-DE-WN)。首先构建一个用于计算系统偏差的权值网络(Weighted Network，WN)；然后对其网络连接权值进行优化，得到最优网络连接权值，再将其输入到权值网络，根据构造的适应度函数，计算出最优系统偏差；最后用其配准目标的传感器量测。

1 权值网络系统偏差估计模型

笔者所提OSPSO-DE-WN算法首先构建一个用于计算系统偏差的WN系统模型，然后用融合优化选择策略的全局最优位置算法优化更新网络连接权值估计，进而得到最优系统偏差估计值。权值网络系统偏差估计模型结构如图1所示。

图1 权值网络模型图

图1中包含开始层、中间层和结束层的权值网络，网络连接权值将层与层连接起来。将网络输入值输入到开始层，通过权值网络的相关加权及非线性运算，将信息从开始层到中间层、然后再到结束层进行层层传递，在网络结束层将网络输出值进行输出。权值网络的各层均由若干个端点组成，其中开始层和结束层的端点数由网络输入和网络输出的维数决定，中间层的端点数是根据经验确定的。

假设有A类和B类传感器量测点迹分别为Zi和Tz，表达式为

Zi=T+Bi+ni，i=1，2，…，M，

(1)

Tz=T+TB+Tn，

(2)

其中，T为目标参考真实点迹，Bi和TB为传感器系统偏差，ni和Tn为随机噪声，Zi代表第i个A类传感器的量测值，M代表传感器的总个数，Tz代表B类传感器的量测值。

A类传感器精度较低，B类传感器精度较高(TB和Tn值极小)，将B类传感器量测作为目标参考真实状态，A类传感器量测数据作为待配准量测。WN系统偏差配准的实质就是将A的量测映射到B上。当随机误差远小于系统偏差(即ni≪Bi，Tn≪TB)时，随机误差可以被忽略，也就是要求网络实现Zi=T+Bi逼近Tz=T+TB；若将A类传感器量测Zi作为网络输入，则系统偏差Bi也就是Zi-Tz为网络输出。网络的输入和输出可由如下描述：

网络输入为Zi=(xi(k)，yi(k))，k=1，2，…，N，i=1，2，…，M。

(3)

网络输出为Bi=Zi-TZ=(xi(k)，yi(k))-(x(k)，y(k)) 。

(4)

而权值网络模型结构的数学描述为

(5)

(6)

(7)

⋮

(8)

(9)

综上所述，网络最终输出值可表示为

(10)

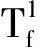
2 OSPSO-DE-WN算法框架

OSPSO-DE-WN算法主要包括两部分：① 用带有优化选择策略的全局最优位置算法优化更新最优网络连接权值估计；② 利用权值网络计算系统偏差值，进而得到最优系统偏差估计值。具体的OSPSO-DE-WN算法框架如图2所示。

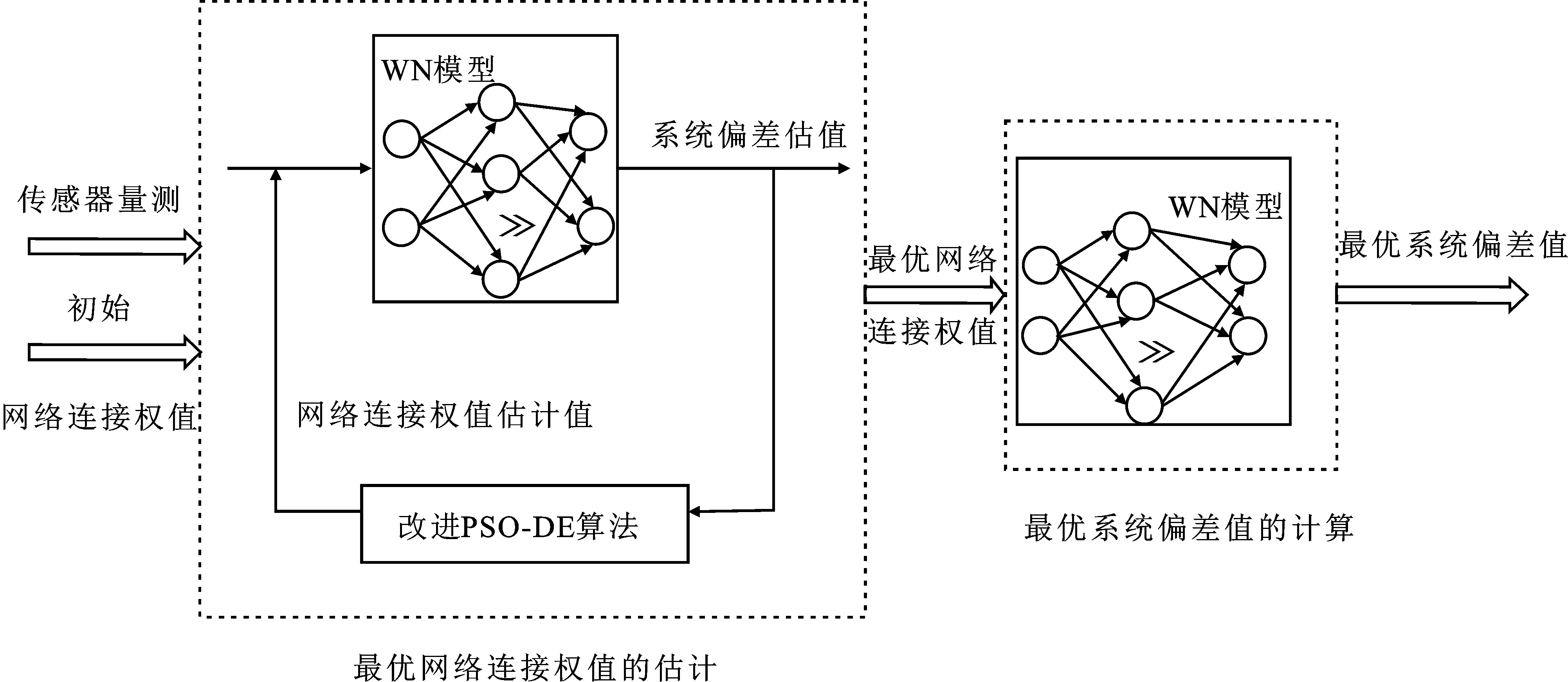
图2 OSPSO-DE-WN算法框架

由图2可知，首先取某时刻的传感器对目标的量测值输入到权值网络，计算出对应的系统偏差值；然后，将系统偏差值输入到文中所提算法中，通过递推学习更新，得到此时刻最优的网络连接权值；最后，将最优的网络连接权值输入到权值网络，计算出此时刻最优的系统偏差估计值。

3 融合优化选择的全局最优位置选择

融合优化选择策略的全局最优位置选择如图3所示。

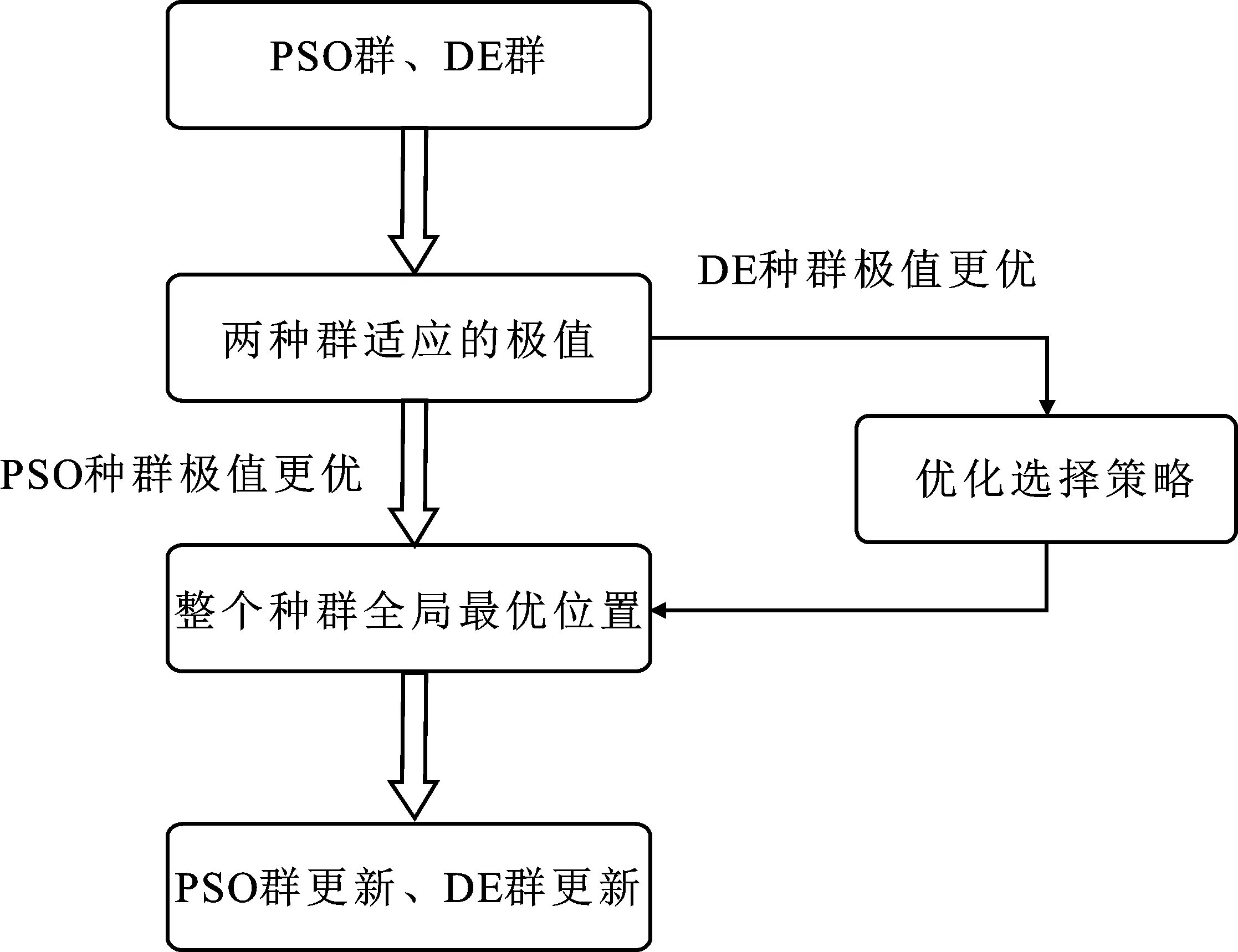
图3 融合优化选择策略的全局最优位置选择

首先，计算每个种群中个体的适应度值并从中选出各种群中的最优个体，若PSO算法种群最优个体优于DE种群，则可直接确定整个种群的全局最优个体，即用PSO算法种群的最优个体作为整个种群的全局最优位置进行整个种群的更新；若DE种群最优个体优于PSO算法种群最优个体，则需要启动优化选择策略来确定整个种群的全局最优位置，即需计算2个最优个体适应度值的差值Df；然后判断Df是否大于所设阈值df，若Df>df，则用DE种群最优个体作为整个种群全局最优位置，否则仍用PSO种群最优个体作为整个种群全局最优位置。这样避免了在2个最优个体适应度值相差较小情况下，利用DE种群最优个体进行更新，不仅能加快收敛速度、节省算法运行时间，同时减小了信息交流误差。

(11)

由式(11)知，Et越小，种群分布越不均匀；Et越大，分布越均匀，种群多样性越好。故差值阈值函数df的公式可设定为

(12)

(13)

同时为了评价粒子优劣，笔者构造了一个适应度函数。适应度值越小，说明参考真实值与系统偏差估计越接近，估计出的系统偏差越准确。在系统偏差配准中，目标是得到最优系统偏差估计。为此可构造包含系统偏差估计和参考真实系统偏差在内的适应度函数：

(14)

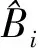
4 仿真实验与结果分析

为了说明笔者所提OSPSO-DE-WN算法在不同轨迹上的可行性及有效性，分别选取在二维平面内作非机动运动和机动运动的目标进行仿真验证。

4.1 仿真场景及参数设置

目标的运动方程以及量测方程如下所示：

X(k+1)=FX(k)+μ(k) ，

(15)

Z(k)=HX(k)+B(k)+φ(k) ，

(16)

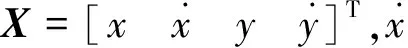
仿真场景1：假设目标在二维平面内作非机动运动，则非机动运动目标的状态转移矩阵表示为

(17)

量测矩阵表示为

(18)

其中，T为采样间隔，设置为2 s。X方向上的速度设置为3 m/s，Y方向上的速度设置为4 m/s。目标状态量X(k)的初始值X(0)设置为[100 m 3 m/s 200 m 4 m/s]T。X和Y方向上的传感器系统偏差值分别设置为-3 m、5 m。

仿真场景2：假设目标在二维平面内作机动运动，则机动运动目标的状态转移矩阵表示为

(19)

量测矩阵表示为

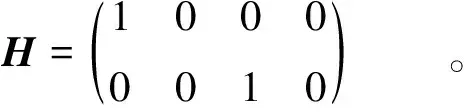
(20)

场景2中，w表示转弯因子。T为采样间隔，取为0.1 s。X(k)的初始值X(0)设置为[200 m 8 m/s 100 m 2 m/s]T，X和Y方向的系统偏差值分别设为-6 m、8 m。在1～100 s，目标右转弯运动，w取值为0.18 rad/s，在101～200 s，目标左转弯运动，w取值为-0.2 rad/s。

表1给出了OSPSO-DE-WN算法中各仿真参数的符号及其具体设置值。

仿真实验采用蒙特卡罗仿真形式，仿真次数设置为50次。采用的仿真环境为Intel i5，主频为3.30 GHz，内存为4.00 GB，仿真软件为Matlab R2014a。

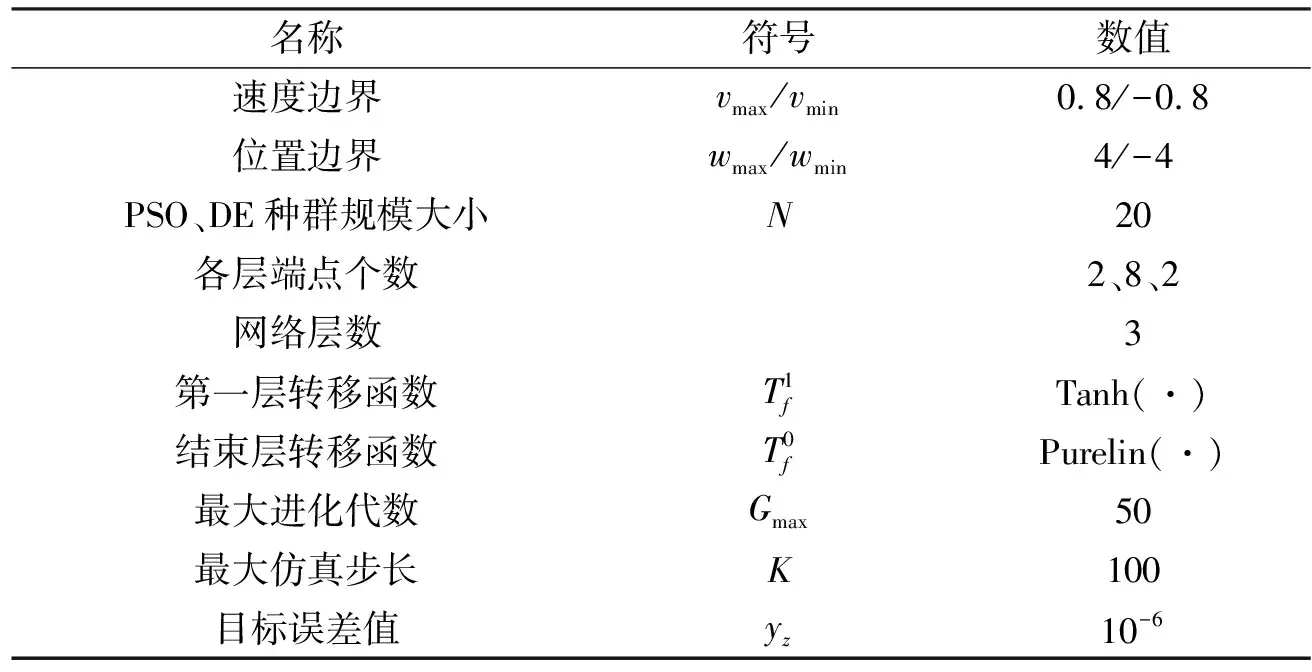
表1 仿真参数设置

4.2 仿真结果及分析

为了证明笔者所提OSPSO-DE-WN算法的有效性和优越性，基于前述所设置的仿真场景和参数，并以系统偏差估计的均方根误差值(RMSE值)作为算法精度的衡量指标，同时选择PSO算法优化WN(PSO-WN算法)、PSO-DE算法优化WN(PSO-DE-WN算法)在非机动运动目标以及机动运动目标两种场景下进行对比分析验证。

首先，验证种群多样性以及个体适应度。以式(11)种群分布熵为衡量种群多样性的指标，以式(14)适应度函数为衡量最优个体适应度指标。其仿真结果如图4和图5所示。

从图4可以看出，随着算法进化代数的增加，笔者所提OSPSO-DE-WN算法的熵值在进化代数为18的时候有一次微小的下降，之后几乎稳定不变。这不仅说明OSPSO-DE-WN算法比PSO-DE-WN算法和PSO-WN算法的种群分布更均匀，也说明OSPSO-DE-WN 算法的熵值是最大的，其种群多样性更加丰富。

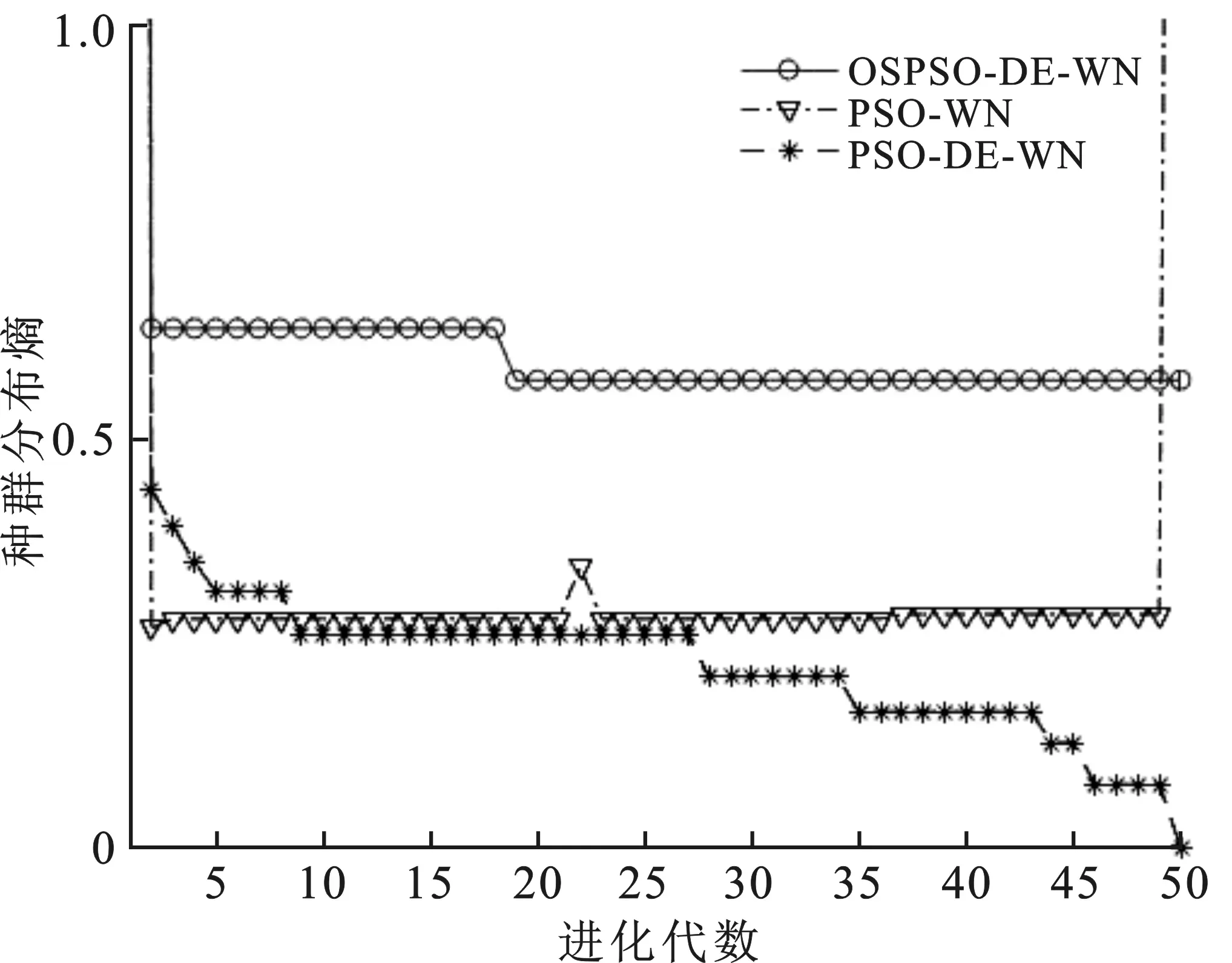
图4 种群分布熵变化曲线

从图5可以看出，OSPSO-DE-WN算法要比PSO-DE-WN算法和PSO-WN算法收敛速度快，而且经过50次的迭代进化，PSO-WN算法得到的最优个体适应度值为0.001 1；PSO-DE-WN算法得到的最优个体适应度值为4.763 1×10-4；OSPSO-DE-WN算法得到的最优个体适应度值为2.019 4×10-5。由式(14)适应度函数可知，适应度值越小，估计出的系统偏差值越接近于参考真实系统偏差值。这验证了OSPSO-DE-WN算法搜索到的适应度值最小，最接近真实系统的偏差。

非机动目标情况下，将作非机动运动的目标的量测值输入到OSPSO-DE-WN算法、PSO-DE-WN算法和PSO-WN算法中，估计出系统偏差值，如图6～图9所示。

图6和图7分别为目标非机动运动下3种算法在X方向和Y方向上的实际输出系统偏差值与参考真实系统偏差值的曲线图。3种算法在X和Y方向上估计出的系统偏差最终均趋于期望输出系统偏差值-3 m和5 m。PSO-WN算法在1～45 s之间出现明显波动，45 s之后基本稳定于参考真实系统偏差值附近。PSO-DE-WN算法在1～35 s之间出现明显波动，35 s之后基本稳定于参考真实系统偏差值附近。从图6和图7均可以看出，OSPSO-DE-WN算法大约在2 s时收敛迅速，之后并逐渐收敛于真实系统偏差值附近。这充分说明OSPSO-DE-WN算法成功避免了两种群在最小适应度值相差较小时，因信息交换出现的不必要信息交流误差，同时也使得收敛速度更快，其运行时间也更短。

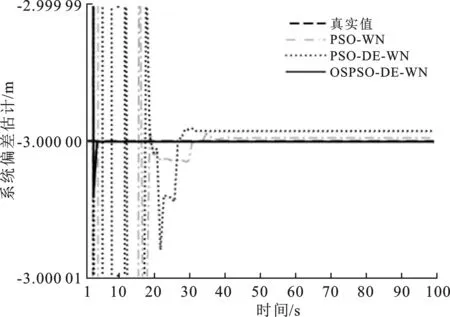
图6 X方向上的系统偏差估计值

在蒙特卡罗仿真次数为50次，以及上述给定的仿真环境下，给出了3种算法的算法耗时，如图8所示，同时也给出了3种算法收敛步长的比较，如图9所示。

图8 3种算法的耗时

从图8可以看出OSPSO-DE-WN算法的运行时间要比PSO-WN算法、PSO-DE-WN算法的短；从图9看出，OSPSO-DE-WN算法的收敛步长最小，进一步证明了笔者所提OSPSO-DE-WN算法的收敛速度要比PSO-WN算法和PSO-DE-WN算法的快。

根据前述结果得出传感器系统偏差估计值，利用该估计值对传感器的量测值进行系统偏差配准。非机动运动目标下3种算法配准前后的轨迹图如图10所示。系统偏差估计的平均均方根误差如图11所示。

图10 非机动运动目标配准前后轨迹

从图10和图11中可以看出，笔者所提算法在具有前述优越性能的情况下，在非机动运动目标下配准后的轨迹比PSO-DE-WN算法和PSO-WN算法更加接近于参考真实轨迹。由图11可以更直观地看出，OSPSO-DE-WN算法在X和Y方向上系统偏差估计的平均RMSE值与PSO-WN算法以及PSO-DE-WN算法相比，数量级减少了一个数量级即101，这证明了在非机动运动目标场景下笔者所提OSPSO-DE-WN算法的精度要高于PSO-WN算法和PSO-DE-WN算法的。

机动目标情况下：将作机动运动目标的量测值输入到OSPSO-DE-WN算法、PSO-DE-WN算法和PSO-WN算法中，仿真结果如图12～图17所示。

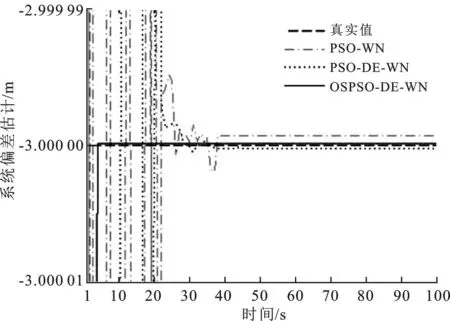
图12 X方向上的系统偏差估计值

图12和图13分别表示机动运动目标下3种算法在X方向和Y方向上的实际输出系统偏差值与参考真实系统偏差值的变化曲线图。可以看出，3种算法在X和Y方向上估计出的系统偏差最终均趋于期望输出系统偏差值-3 m和5 m。PSO-WN算法在1～25 s之间出现明显波动，25～40 s之间轻微波动，40 s之后基本稳定于参考真实系统偏差值附近。但由于PSO-DE-WN算法融合了DE算法和PSO算法，使种群的多样性增加，算法收敛速度变快。从图12和图13中也可以看出，在1～24 s之间出现波动，31 s之后基本稳定于参考真实系统偏差值附近。OSPSO-DE-WN算法大约在2 s时收敛迅速，之后稳定于参考真实系统偏差值附近。这充分说明OSPSO-DE-WN算法即使在机动运动目标情况下，也能有效避免两种群在最小适应度值相差较小时，因信息交换出现的不必要信息交流误差，同时运行时间也更短即收敛速度更快。

设定蒙特卡罗仿真次数为50次，在前述仿真环境下，从图14给出了3种算法的算法耗时，同时图15也给出了3种算法收敛步长。从图14可以看出，OSPSO-DE-WN算法的运行时间为266.4 s，要比PSO-WN算法和PSO-DE-WN算法的短。从图15看出，OSPSO-DE-WN算法的收敛步长要比PSO-WN算法和PSO-DE-WN算法小得多。这进一步验证了OSPSO-DE-WN算法的收敛速度最快。

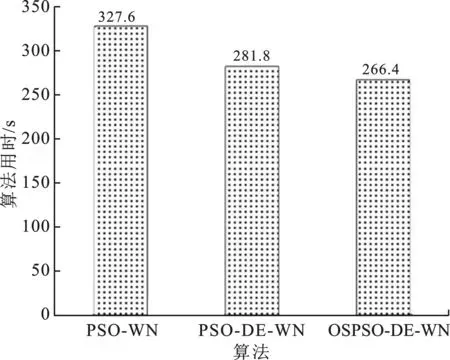
图14 3种算法的耗时

根据文中前部分得出的传感器系统偏差估计值，利用该值对传感器的量测值进行系统偏差配准。目标机动运动下3种算法配准前后的轨迹如图16所示。

从图16中可以看出，笔者所提算法在具有前述优越性能的情况下，在机动运动目标下配准后的轨迹比PSO-WN算法、PSO-DE-WN算法更加接近于参考真实轨迹，使得系统偏差配准能够更好地进行。从图17可以更直观地看出，OSPSO-DE-WN算法在X和Y方向上系统偏差估计的平均RMSE值与PSO-WN算法以及PSO-DE-WN算法相比，数量级减少了一个数量级即101，这充分说明在机动运动目标场景下，OSPSO-DE-WN算法的精度高于PSO-WN算法以及PSO-DE-WN算法的。

图16 机动运动目标配准前后轨迹

5 总 结

针对系统偏差模型难以构建、粒子群算法出现种群多样性变小和PSO-DE算法出现信息交流误差的问题，笔者提出了一种带有优化选择策略的差分粒子群算法优化权值网络的系统偏差配准——OSPSO-DE-WN算法。该算法首先构建了一个用于计算系统偏差的权值网络，然后采用改进的优化策略对WN网络连接权值进行优化更新，最后得到系统的最优偏差估计。实验结果表明，该算法适应度值最小，无论在非机动运动目标还是机动运动目标运动场景下，都可有效提高种群多样性并避免信息交流误差，极大提高了收敛速度以及运算精度。