适用于BOC及其衍生信号的无模糊跟踪算法

孙希延，宋少杰，纪元法，梁维彬，李有明

(1.桂林电子科技大学 广西精密导航技术与应用重点实验室，广西壮族自治区 桂林 541004；2.国家与地方卫星导航定位服务联合工程研究中心，广西壮族自治区 桂林 541004)

随着卫星导航技术的发展和推广，卫星通信频带信号激增，频带拥挤、信号间的射频干扰、导航系统间的不兼容问题越来越严重，二进制偏移载波调制信号作为解决方案被提出[1]。由于二进制偏移载波调制信号具有窄相关主峰和频谱分裂特点，相比传统的BPSK信号跟踪精度更高，抗多径性能也更加优良。但是，由于二进制偏移载波调制信号相关函数的多副峰特性，造成了二进制偏移载波调制同步过程中具有严重的跟踪模糊问题，对定位精度有很大的影响。因此，如何能够在消除二进制偏移载波调制信号的模糊性的前提下，又能保留其窄相关主峰特性，提高跟踪精度和抗多径性能，已经成为当前导航领域的研究热点[2-3]。

二进制偏移载波调制信号具有许多优点，但其自相关函数的多峰特性使得导航接收信号的跟踪更加困难。为了解决这个问题，近年来的相关研究提出了许多优秀的成果。如文献[4-6]中的单边带算法，该方法的思想是将二进制偏移载波调制信号分为多个类BPSK信号，分别进行处理，然后进行非相干积累，如文献[5]中的BPSK-like算法。利用该方法虽很好地消除了相关副峰，但也牺牲了二进制偏移载波调制信号的窄相关主峰特性。文献[7-8]中的无模糊检测算法，如Bump-jump和DET(Double Estimation Technique)算法等都是通过增加相关器数量来检测二进制偏移载波调制号同步过程中出现的跟踪模糊现象。这种方法需要较长的检测和恢复时间，不适用于弱信号。文献[9-11]中的边峰消除技术(Side-pesk Cancellation，SC)，利用局部辅助信号进行特定的组合算法来实现对相关副峰的消除或抑制，保留或生成一个新的单主峰相关函数。例如ASPeCT算法，但该方法仅适用于sin-BOC(n，n)信号；SCPC边峰消除算法虽适用于任何二进制偏移载波调制信号，但牺牲了二进制偏移载波调制信号的窄主峰特性。

为了实现对二进制偏移载波调制信号的无模糊跟踪，笔者提出一种子函数组合相关的无模糊跟踪算法。利用笔者提出的形状码向量表示出自相关的各个子函数，然后将子函数通过重构规则进行组合，得到无旁峰干扰的新的相关函数。仿真表明，这种方法能有效地适用于对BOCs(m，n)和CBOC(6，1，1/11)信号的跟踪。

1 二进制偏移载波调制相关特性及形状码

1.1 二进制偏移载波调制信号模型

二进制偏移载波调制基准信号的数学表达式为

SBOC(t)=c(t)s(t) ，

(1)

其中，c(t)为伪随机码，s(t)为信号副载波。

伪随机码c(t)的数学表达式如下：

(2)

其中，{Ci}表示第i个码片的符号值，Ci∈(-1，1)；Tc为伪码码片的宽度；PTc(t)是周期为Tc，幅值为1的矩形脉冲信号。

方波副载波将伪随机码扩频符号分为N份，每份长度为Ts=Tc/N，因此副载波s(t)的数学表示为

(3)

其中，Ts是副载波半周期，PTs(t)是周期为Ts、幅值为1的矩形脉冲信号；N表示二进制偏移载波调制信号中一个伪码长度所对应的副载波半周期个数；dj∈{1，-1}(j=0，1，…，N-1)，对于正弦或者余弦调制二进制偏移载波调制信号，dj取值可以不一样。

MBOC信号的功率谱由占比10/11的BOC(1，1)信号的功率谱和占比1/11的BOC(6，1)信号的功率谱组合而成。CBOC(6，1，1/11)是MBOC信号的一种实现形式，由基准sine-BOC(1，1)和sine-BOC(6，1)信号以一定的功率比例组合而成，

(4)

1.2 BOC形状码向量

将式(3)中的dj∈{1，-1}(j=0，1，2，…，N-1)定义为形状码，由形状码组成的向量dj∈{1，-1}(j=0，1，2，…，N-1)，称为形状码向量。对于正弦型(BOCs)和余弦型(BOCc)信号可以用不同的形状码向量d表示，如图1所示。

(5)

1.3 通用互相关函数

结合式(2)和式(3)以及上述形状码向量的定义，可以得到统一的BOC基带信号的数学表达式还可以表示为

(6)

根据形状码向量的概念，假设任意两路扩频信号BOC的子载波调制信号分别为

(7)

其中，s1(t)和s2(t)具有相同的fs和N，形状码向量和可以不同，因此，具有理想相关特性的PRN序列的直接扩频信号的相关函数可表示为

(8)

根据方波自相关函数的特性[12]：

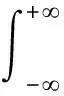
(9)

其中，ΛTs(τ)为中心在零点、底边宽度为2Ts、幅值为1的等腰三角函数。因此式(8)可以表示为

(10)

同理，结合式(3)，CBOC(6，1，1/11)信号的副载波可表示为

s(t)=w1sBOC(1，1)(t)+w2sBOC(6，1)(t) ，

(11)

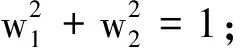
(12)

(13)

2 算法分析

2.1 无模糊跟踪算法分析

根据式(10)二进制偏移载波调制类信号相关函数的通用公式，二进制偏移载波调制自相关函数是由多个形状码图形组合得到的图像。对于BOCs(m，n)调制信号，其形状码向量为d=[1 -1 1 … -1]N，其中N=2m/n，结合式(10)相关函数，可得到以矩阵形式表示的BOCs(m，n)的自相关函数：

(14)

图2 BOC(1，1)信号自相关函数组成

从式(14)可以看出，BOCs(m，n)自相关函数的表达式中包括多个三角函数ΛTs，其中任意三角形Λ(τ-kTs)的峰值在相邻三角形Λ(τ-(k-1)Ts)的零值处。相关函数的任意两个峰值之间是分段线性的。以BOCs(1，1)自相关函数为例，根据式(14)，可得其形状码向量是dj1=[1，-1]和dj2=[1，-1]，对应的相关组合为：dj10·dj20·ΛTs，dj11·dj21·ΛTs，dj10·dj21·Λ(τ+Ts)和dj11·dj20·Λ(τ-Ts)，分别记为L1，L2，L3和L4。BOCs(1，1)的相关组合如图2所示。

图2中L1和L2完全重合且关于Y轴对称，L3和L4也关于Y轴对称，且L1和L2的两斜边分别与L3，L4的两斜边平行，所以L1+L3和L2+L4在幅值上完全相同。将L1+L3记为C1，L1+L3记为C2，结合图2，可得组合相关C1和C2的具体形状。

结合上述推导过程可知，式(14)矩阵中，主对角线上的形状码向量构成的三角形关于Y轴对称，关于主对角线对称的任意两队形状码向量组成的图形也关于Y轴对称。对于BOCs(m，n)信号，将主对角线下方的形状码向量进行相加，记作C1，主对角线上方进行相加，记作C2。可以得到组合后的图形C1和C2关于Y轴对称。可表示为

RC1(τ)=RC2(τ)

(15)

结合上述分析，给出的BOCs(1，1)的BOCs(2，1)的组合相关函数C1和C2，如图3(a)所示。

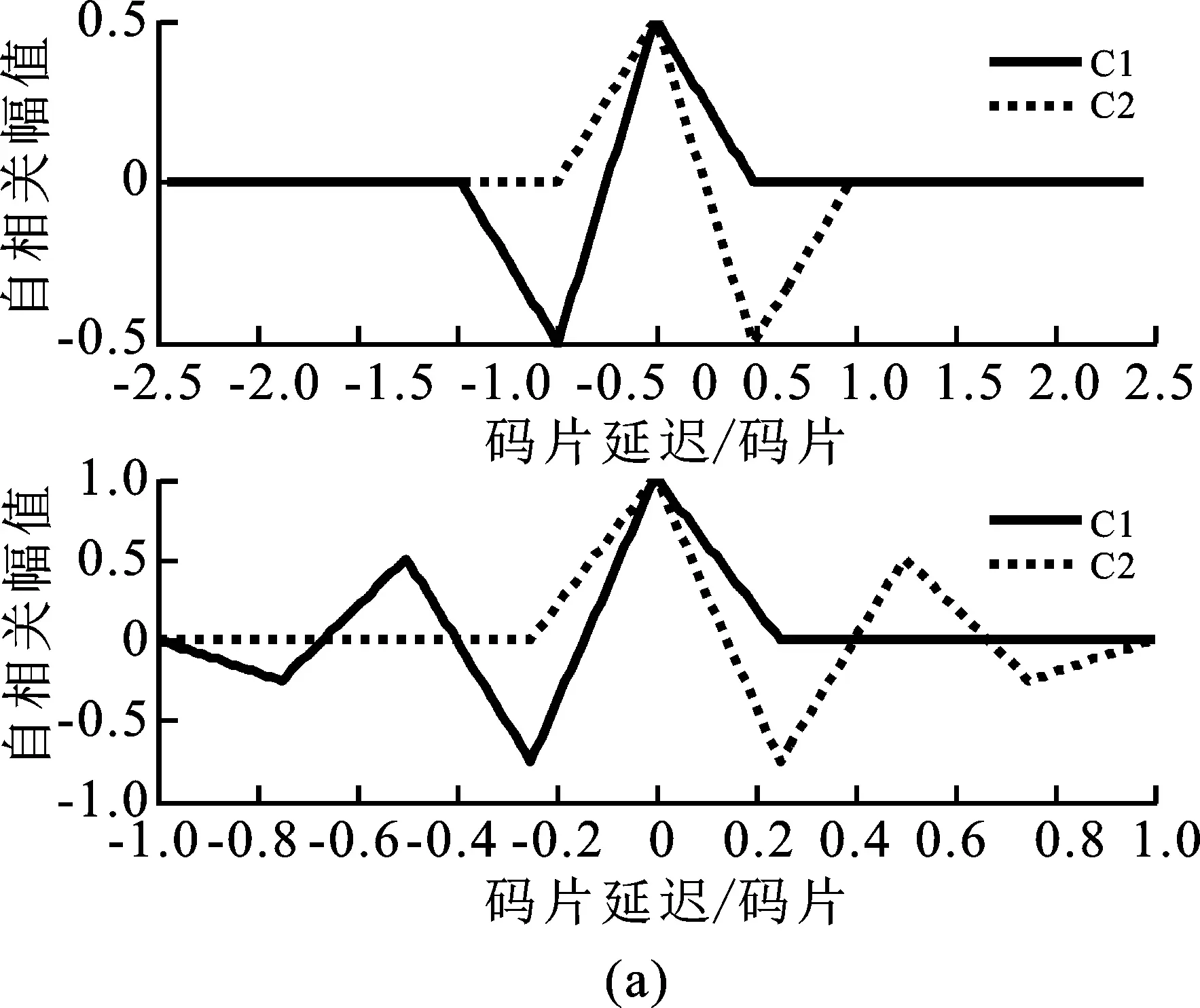
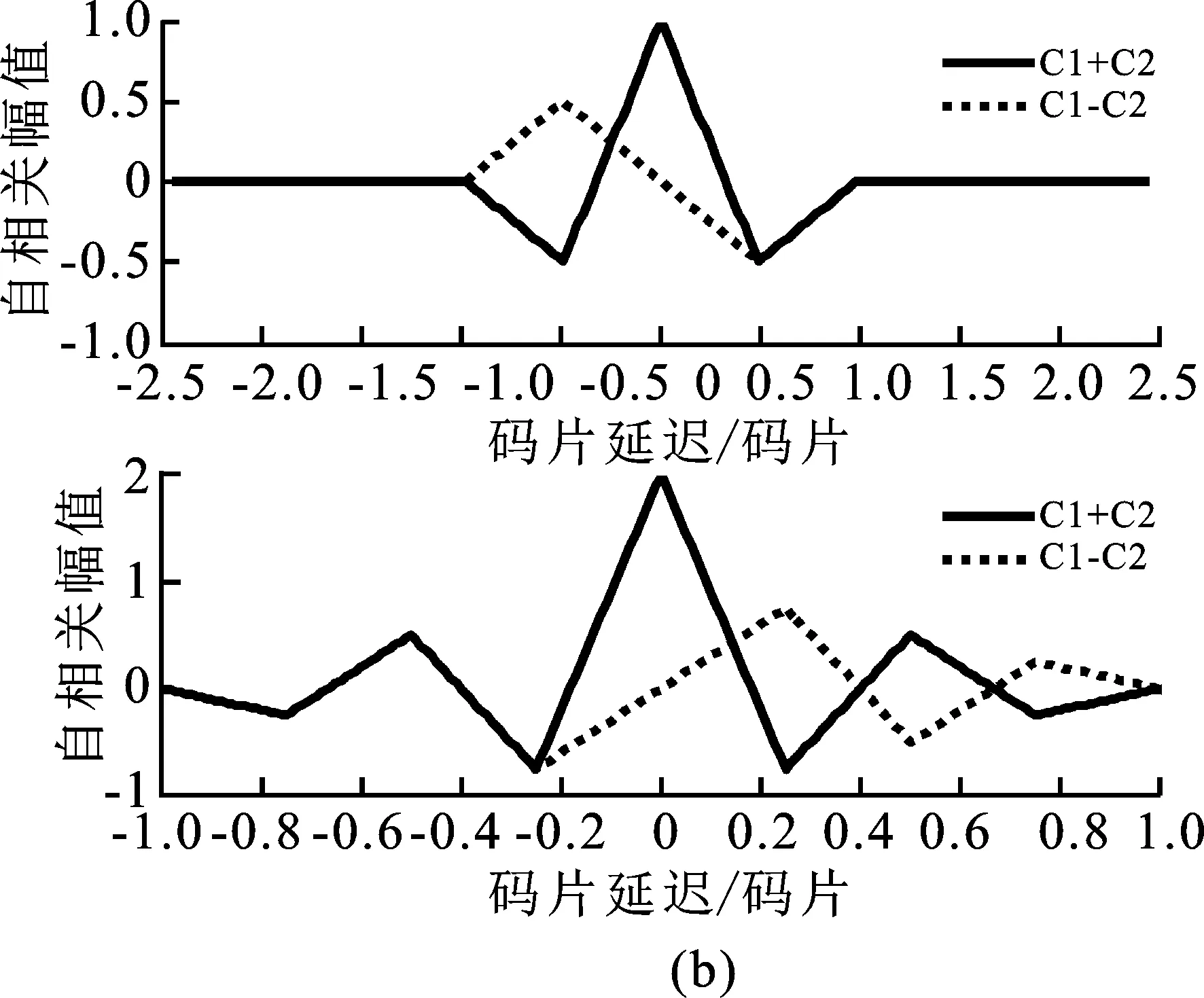
图3 BOC(1，1)的BOC(2，1)子相关组合函数、子相关函数向量组合以及重构相关函数

从图3(a)可以看出，BOC(1，1)的BOC(2，1)的组合相关函数C1，C2都关于Y轴对称，且二者C1和C2的波峰峰值相等。该特性将作为去除二进制偏移载波调制信号模糊性的重要支点。将相关函数C1，C2进行数学上的相加相减，可得到如图3(b)所示的向量图形组合。图3(b)中，C1+C2是BOC信号自身的相关函数，对于BOC(1，1)，0码片处只存在一个窄主峰，且±0.5码片处副峰幅值相等；同样地，对于BOC(2，1)，0码片处也只有一个主峰，其余副峰的幅值也相等。根据该特性，设计重构相关函数可表示如下：

Rp=|RC1|+|RC2|-|RC1-RC2| ，

(16)

根据重构的相关函数的表达式，可得到二进制偏移载波调制信号的重构相关函数，如图3(c)所示。

BOCs(m，n)信号的无模糊跟踪算法也可以用在CBOC(6，1，1/11)信号无模糊跟踪上，以原CBOC信号的伪码构造两路本地信号，通过笔者提出的重构规则得到仅保留主峰的相关函数。构造出的2路本地信号的表达式分别为

(17)

利用CBOC(6，1，1/11)信号的生成原理以及上述二进制偏移载波调制信号本地码的设计原理，可将CBOC(6，1，1/11)信号的生成信号波形表示为

(18)

式(18)中的dj(e1)，dj(e2)和dj(o1)，dj(o2)分别对应地是BOC(6，1)和BOC(1，1)，由二者根据设计原理设计出的4路本地码，w1和w2是CBOC基带信号中组成副载波的BOC(6，1)和BOC(1，1)的比例值。因此，构造的本地码的形状码向量为

(19)

(20)

通过式(20)可以发现RE(τ)和RO(τ)关于Y轴对称，即RE(τ)=RO(-τ)。结合文中提出的重构相关方法，对CBOC进行仿真，可得到无模糊相关函数如图4所示。

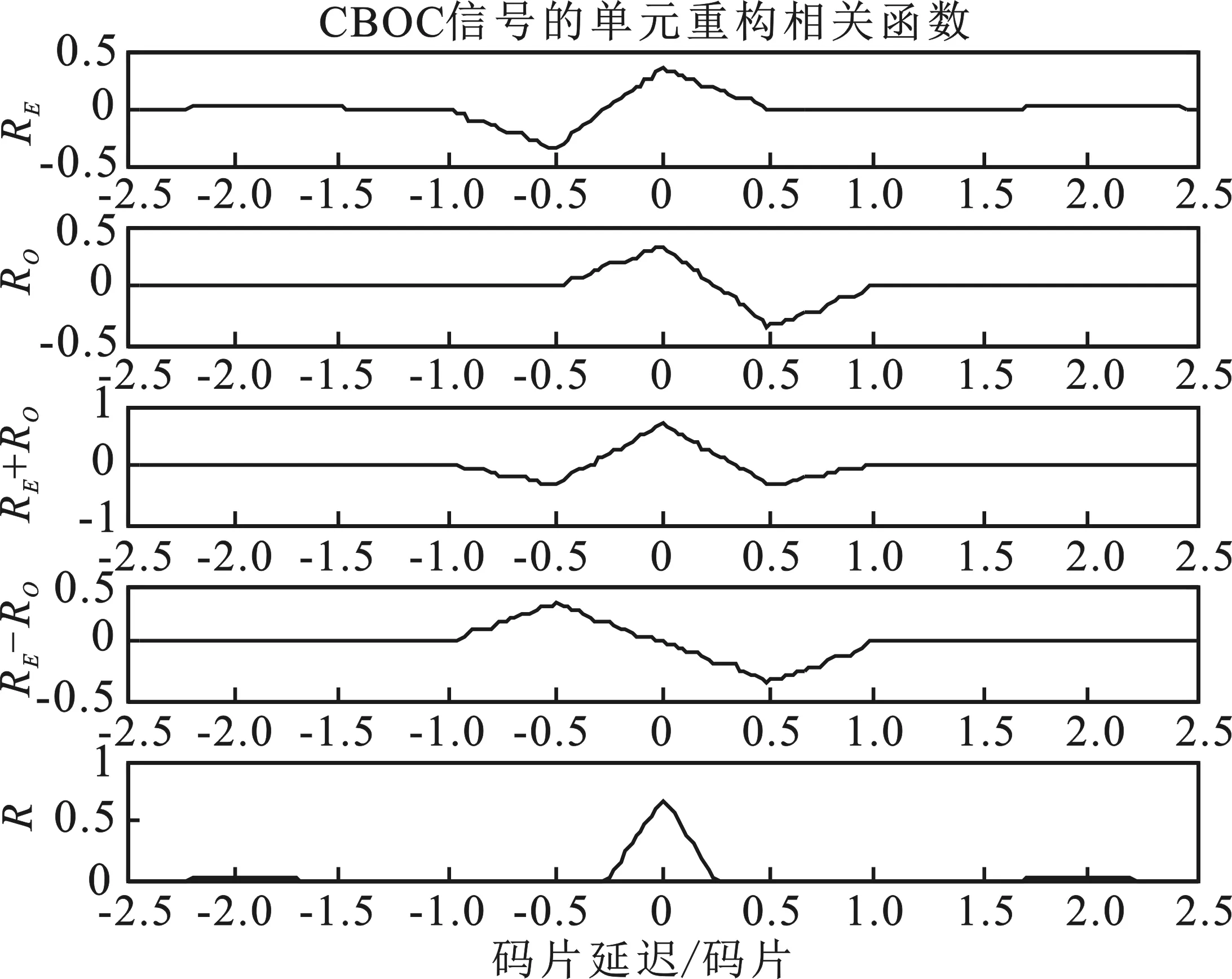
图4 CBOC(6，1，1/11)信号相关重构过程

从图4中可以直观地看出，仿真图中显示的波形和推导的结果一致，RE(τ)和RO(τ)在相同的码相位处，副峰的幅值也相同，再利用式(16)所述的重构方法，得到了一个完全消除边峰的新相关函数，并且主峰更加窄，保留了CBOC信号本身的优势。

2.2 改进后的跟踪环路结构

图5为笔者基于调制信号形状码向量的跟踪算法的码跟踪环路结构，与传统的延迟跟踪环路(DLL)相比略有不同。在正交和同相支路中需额外增加4个相关器，通过本地产生的辅助信号，可以得到改进后的可实现无模糊跟踪的非相关鉴相输出函数。对接收到的中频信号进行载波剥离的同时，码跟踪环路产生二进制偏移载波调制信号和辅助信号的超前和滞后版本。本地码与接收信号进行相关后，通过码鉴相器和数控振荡器(NCO)对本地码相位进行调整，实现对二进制偏移载波调制信号的精准跟踪。相比传统的码跟踪环路结构，减少了滤波电路，结构有了简化，硬件的实现复杂度也有所降低。

图5 码跟踪环路结构

3 仿真分析

3.1 去模糊有效性

为了验证文中模糊消除方法的通用及有效性，仿真以BOC(1，1)，BOC(2，1)和CBOC(6，1，1/11)信号为例，同时采用ASPeCT[10]算法，SCPC[13]算法和BPSK-like算法[5]进行对比。仿真结果表明，BPSK-like算法和SCPC算法虽然可以消除信号的边峰，但是牺牲了二进制偏移载波调制信号的窄相关主峰特性，得到的相关函数曲线也极不平滑，这会影响信号的跟踪精度。ASPeCT的主峰相比原相关变窄，但相关函数的副峰并未完全消除，在信号较弱的情况下，容易产生误捕误锁问题，影响导航接收机的定位精度。相比之下，文中方法不仅完全消除了边峰，还保留了调制信号的窄相关优势。

图6所示为归一化自相关函数的对比。

(a) BOC(1，1)

3.2 鉴相曲线

假设接收机前端带宽无限大，将鉴相器相关间隔设置为0.1Tc。对比算法采用ASPeCT，BPSK-like和Unit Correlation[6]。仿真结果表明：使用传统EMLP(Early Minus Late Power)方法的鉴相曲线均存在较多稳定的误锁点。ASPeCT算法能消除误锁点，但只适用于BOC(1，1)和CBOC(6，1，1/11)信号。BPSK-like和Unit Correlation对3种调制信号均有效，但二者的斜率增益[14]均小于传统EMLP和文中的算法，斜率增益越大，信号的跟踪抖动精度和抗噪声性能就越高。文中的跟踪算法，在消除模糊跟踪点的同时，加强了信号的抗噪性能。

图7所示为鉴相函数的对比。

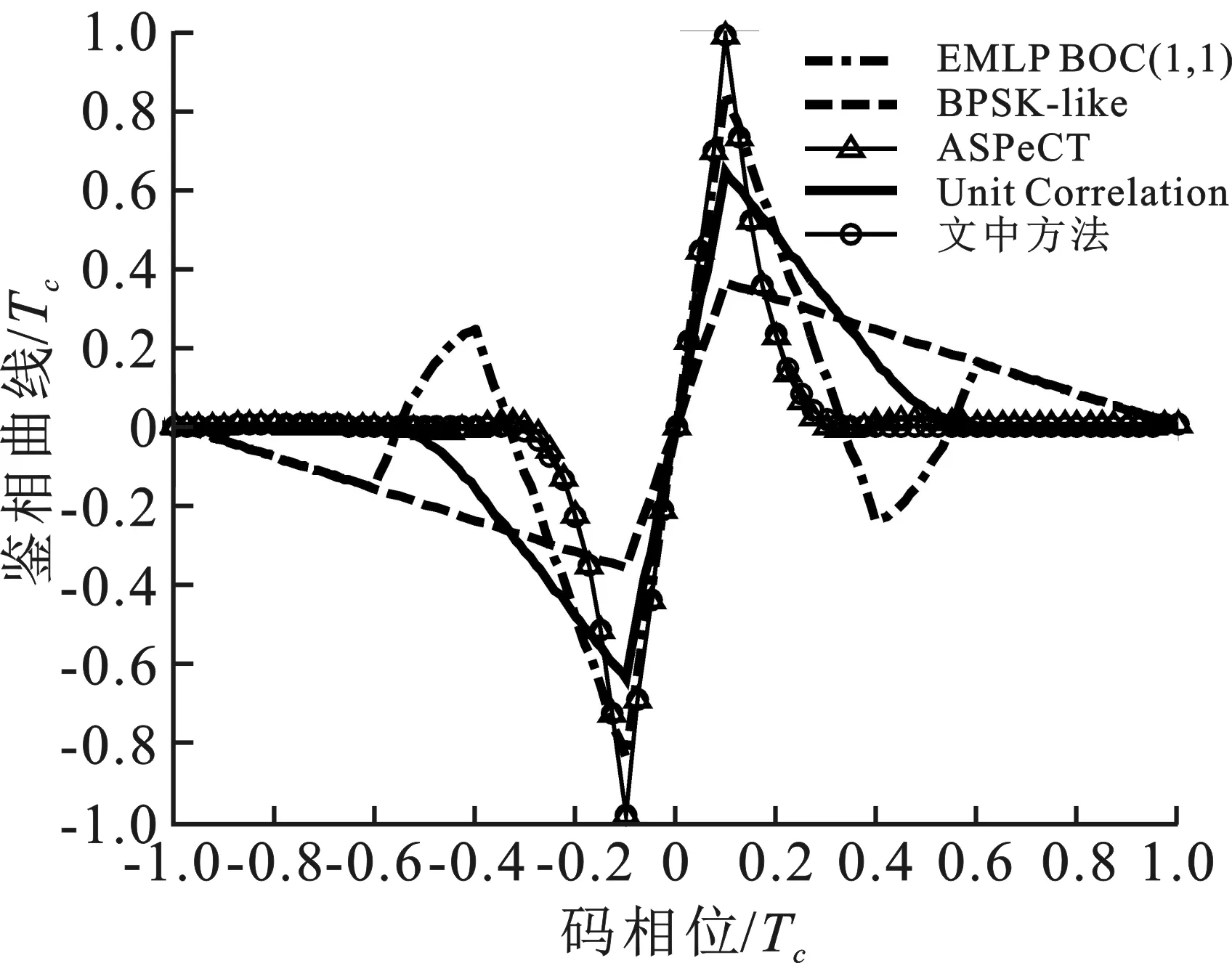
(a) BOC(1，1)

3.3 抗噪声性能

热噪声是造成跟踪误差的另一个主要原因，码跟踪环路误差标准差也是衡量信号跟踪算法抗噪声性能的重要指标[15]。设置单边带带宽BL为1 Hz，Tcoh相干时间为1ms，相关器间隔d为0.1Tc。采用传统EMLP，ASPeCT，BPSK-like和Unit Correlation与文中算法作对比。从节3.1的仿真分析中可得ASPeCT算法不适用与BOC(2，1)，故在此不多做分析。从图10中可以看出，相同条件下，BPSK-like算法和SCPC算法的码跟踪误差较大，对于BOC(1，1)，BOC(2，1)信号，EMLP，ASPeCT和Unit Correlation算法得到的结果与文中算法最为接近，且对于CBOC(6，1，1/11)信号，Unit Correlation算法的码跟踪误差略小于文中所提算法，码跟踪性能良好。这主要是因为信号相关的窄主峰特性保留，得到了较高的鉴相增益。相比于BPSK-like，对于BOC(1，1)，BOC(2，1)和CBOC(6，1，1/11)信号，采用笔者提出的算法后，码跟踪误差标准差分别减少了0.045Tc，0.031Tc，0.078Tc，说明这种方法的抗噪声性能较好。

图8所示为码跟踪误差的标准差对比。

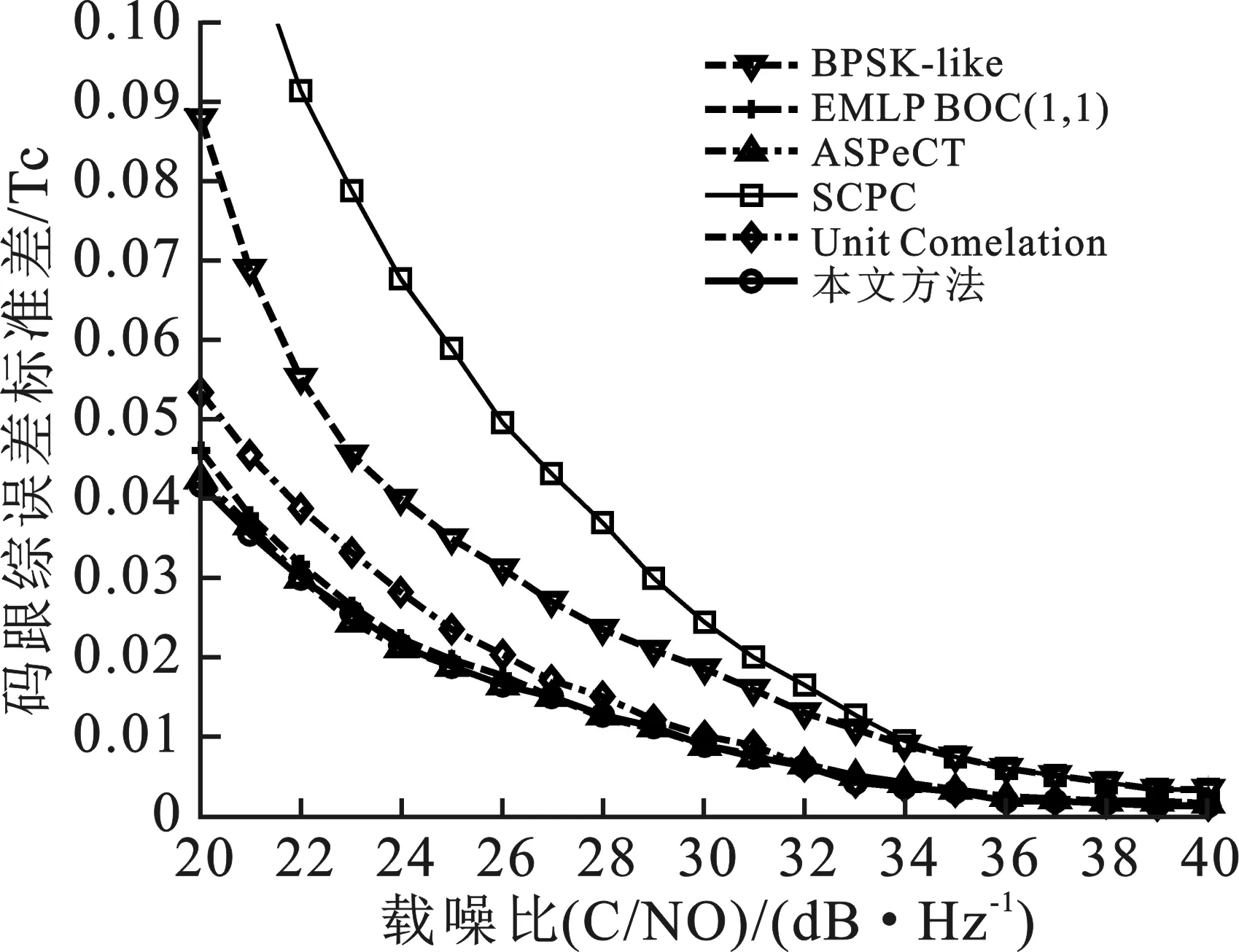
(a) BOC(1，1)

3.4 计算复杂度分析

在跟踪过程中使用笔者所提跟踪算法，可节省大量计算。对接收信号进行采样，数据点N为818 400，多普勒搜索的范围为±10 kHz，搜索步骤设定f=500 Hz，因此多普勒搜索的频点为fbin=21。对比试验中的单元相关算法和文中所提算法需要5次快速傅里叶变换运算，2次复数乘法和2次实数乘法运算[6]。ASPeCT和SCPC需要8次快速傅里叶变换运算、4次复数乘法和2次实数乘法[10]。BPSK-Like方法需要6次快速傅里叶变换运算、1次复数乘法和4次实数乘法[16]。根据快速傅里叶变换的属性，有NlbN复数乘法和NlbN复数加法。一次复数乘法等于实数和2个实数加法的4次乘法，一个复数加法是实数的2次加法。总计算的比较详见表1。

表1 算法运算量对比

从表1可以看出，笔者所提跟踪算法及单元相关的总计算量约为ASPeCT算法的41.46%，约为BPSK-Like算法的57.32%。

4 结束语

笔者对二进制偏移载波调制信号相关函数多峰特性引起的误捕误锁问题进行研究，提出了一种适用于BOC(m，n)和CBOC(6，1，1/11)信号的无模糊跟踪算法。该跟踪算法通过提出的形状码向量推导二进制偏移载波调制信号的通用相关函数模型，然后得到调制信号的自函数表达式，再将子相关函数以文中提出的无模糊相关重构规则进行组合，得到边峰完全消除的窄主峰相关函数。相比传统的跟踪算法，笔者提出的跟踪算法在去模糊有效性，鉴相输出特性，抗多径性能等方面体现出了良好的性能。这为新一代导航系统与DOA、三维成像、雷达等系统的应用结合提供了一个先决条件。