索引边缘几何卷积神经网络用于点云分类

周 鹏，杨 军

(1.兰州交通大学 电子与信息工程学院，甘肃 兰州 730070；2.兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070)

随着激光雷达、RGB-D深度相机等三维扫描设备的广泛应用，点云数据获取更加便捷，针对点云数据的高效识别和分类已成为计算机视觉领域亟待解决的问题。以卷积神经网络为代表的深度学习模型在二维图像识别领域取得了巨大的成功。然而，由于点云模型具有无序性、稀疏性、数据有限性等特点，使得采用深度卷积神经网络进行处理存在一定难度。一些研究将其转换为体素[1-2]后使用卷积神经网络进行处理，但转换过程会带来量化损失、局部特征信息丢失、计算效率低等问题。QI等[3]提出了可直接处理无序点云的PointNet模型，其采用多层感知机提取每个点的高维特征，在特征空间维度上使用最大池化进行特征融合，进而提取出点云的全局特征描述符用于三维模型分类。然而，PointNet仅关注点的全局特征，缺乏捕捉局部细粒度特征的能力。QI等[4]改进了PointNet，提出的PointNet++模型，在局部点云范围内迭代使用PointNet提取多尺度特征。该网络虽然考虑到点云的局部区域特征，但没有考虑到点与点的位置关系，缺乏捕捉各个点之间几何特征的能力，且PointNet++计算复杂度高，耗费更多的时间和硬件资源，限制了其在轻量化网络环境中的应用。

5G时代的来临和移动互联网的快速发展，为便携设备提供了更为广阔的应用领域。对基于移动设备的三维模型识别与分类的应用，不仅要求构建的轻量级神经网络具有架构精简、训练参数少、运行速度快等特点，而且要确保具有良好的识别分类性能。为提高小型嵌入式设备的处理能力，需要同时满足存储空间、功耗和运算速度的要求，设计适用于便携式设备的轻量化深度神经网络架构是解决该问题的关键，也逐步得到了学术界和工业界的广泛关注[5]。闫林等[6]提出一种采用双路神经网络的轻量级模型，避免了多尺度学习引入的复杂结构和计算，挖掘了全局特征和局部细粒度特征，但该模型通过手动设置近邻点参数，限制了算法对不同数据的适配能力。白静等[7]提出面向点云模型分类的深度网络原型，通过控制变量法完成网络参数设置及优化，形成结构紧凑、参数合理的网络模型，但其无法很好地捕捉由度量空间引起的局部结构问题，因而限制了该网络对精细场景的识别和对复杂场景的泛化能力。文献[8]采用全密集连接方法将网络的所有卷积层互连，提高了特征的利用率，减少了每一层的参数大小，该网络对大目标点云分类效果较好，但对小目标点云容易造成误分类。文献[9]提出一种无反馈的点跳跃框架PointHop，通过描述符来表示点及点上单跳邻居之间的关系。为控制与点相关联的属性向量维度过快增长，引入Saab Transform[10]对每个PointHop单元的属性降维。该架构虽然在训练时间上大幅缩减，但网络模型参数数量过多，易导致模型复杂度增加。文献[11]提出了一种树形结构的无监督的特征学习模型PointHop++，每个叶子节点对应一个标量特征，并根据特征的判别能力，引入交叉熵准则对特征进行自动排序，但该网络将点云数据一次性输入训练，导致内存占用过大，训练时间过长，难以实现轻量化。文献[12]通过度量相邻点之间的距离关系，采用边缘卷积(Edge Convolution，EdgeConv)操作，一定程度上提高了网络识别性能，但它仅考虑一个差值特征，忽略了邻居点与中心点的方向问题，无法捕捉更抽象的深层语义特征信息。

鉴此，笔者提出基于索引边缘几何卷积神经网络进行点云分类，该网络在具有良好分类准确率的同时实现了轻量化。主要创新点和贡献有：

(1) 在PointNet网络的基础上，设计轻量化网络结构原型。对网络原型中“非敏感层”结构进行裁剪，设置末尾卷积层的通道数为输入层采样点个数，达到与复杂深度网络模型接近的匹配准确率。

(2) 考虑到不同特征空间之间的差异，在每一层定义新的局部区域。进行边卷积之前，先根据k近邻确定新的局部区域，再加入相邻点之间的向量方向，使局部信息损失进一步降低。

(3) 构建索引边缘几何卷积神经网络，将不同卷积层的输出特征映射并进行索引跳跃连接，有效避免了深度神经网络的梯度消失和梯度爆炸的问题，得到信息丰富的边缘向量。

1 点云特征提取

传统的点云特征提取方式，通常是为了解决特定领域的问题而设计的，很难推广到新的特征提取任务。基于深度学习的点云特征提取可分为基于点的提取方法和基于树的提取方法[13]。 前者直接将原始点云作为深度学习的输入；后者首先使用一个k维树(kd-tree)结构对点云进行规则化处理，再将处理后的数据提供给深度学习模型。Geo-CNN[14]对每个点及其局部邻域应用一种称为“GeoConv”的类卷积运算，在提取中心点与相邻点的边缘特征时，通过逐步扩大卷积的接受域，以分层提取特征并保持沿层次的点的几何结构。考虑到点间的方向信息，计算点投影到极坐标的值，再与两点之间的距离进行加权求和，解决了局部特征提取不全的问题。

1.1 基于边缘卷积的特征提取

基于边缘卷积的特征提取使用k近邻的方式定义离某点最近的k个点为邻近区域。首先提取中心点与邻近点之间的边特征，然后在边特征上进行卷积操作。距离中心点Pxi最近的邻域点集为{j：(i，j)∈ε}，与之相关的有向边集合为 {(i，ji1)，…，(i，jik)}。边缘特征定义为eij=hθ(Pxi，Pxj)，其中，hθ是使用可学习参数θ构成的非线性函数，在hθ操作上添加一个非对称聚合操作Ψ，得到边缘卷积第i个顶点的特征输出：

(1)

将中心点的特征、中心点与邻域点的特征差串联后输入多层感知器(Multi Layer Perceptron，MLP)，使边特征融合点之间的局部关系和点的全局信息，即hθ(Pxi，Pxj)=hθ(Pxi，Pxj-Pxi)。在得到n个边特征之后，进行最大池化得到该局部区域的单一特征，通过这种方式叠加多层卷积，逐层提取、整合局部信息。

边缘卷积层局部邻域图的构造由多层感知机实现。对相邻点的边缘逐层卷积时，每一层都会输出新的点云图结构和特征空间，得到新的局部区域。引入点间差的方法，考虑了点之间的几何相关信息，解决了PointNet和PointNet++架构中局部特征提取不全的问题，然而存在忽略点的方向信息的问题，所以笔者提出索引边缘几何卷积神经网络(Index Edge Geometric Convolutional Neural Networks，IEGCNN)。

1.2 索引边缘几何卷积神经网络的特征提取

图1 点云的极坐标表示

索引边缘几何卷积神经网络IEGCNN在边缘卷积网络中加入点的方向信息，用极坐标系对三维点云进行建模，将边缘网络架构中点与点之间的关系投影到三维坐标系。计算极坐标投影到不同坐标轴的值，并与两点之间的距离进行加权求和，得到当前点的特征值。

如图1所示，在极坐标系中设Pxj的坐标为(x，y，z)，对点Pxj进行三维坐标投影运算，得到其所在卦限的投影长度和夹角：

(2)

其中，Plj表示向量(x，y，z)的模长度，Pd表示投影长度，Pθ表示夹角。

假设一个F维点云含n个点{Px1，Px2，…，Pxn}∈RF，在F维点云中，n表示点的个数，F表示通道数。IEGCNN卷积层的输入为n×Øin，输出为n×Øout，Øin和Øout分别表示每一个点特征的输入和输出的维度。对于每个点，根据k近邻(k-Nearest Neighbor，kNN)算法和网络超参r构造局部球形邻域(r表示球形邻域半径式(3))，可构造以Pxi为中心点的球形邻域N(Pxi)，得到若干个邻域点后计算出中心点Pxi的特征输出Pxi′(式(1))，再计算中心点的特征向量(式(4))，其中，权值矩阵MF的维度为Øin×Øout。

N(Pxi)={Pxj|‖Pxj-Pxi‖≤r} ，

(3)

(4)

其中，f(pi| (l))表示pi点在l层的特征向量，MF表示用来提取中心点特征的权值矩阵，w(Pxi，Pxj，r)表示中心点Pxi和不同的邻域点Pxj之间的距离加权，其随‖Pxj-Pxi‖单调递减。随着半径r的增大，球形邻域的感受野逐渐增大，与中心点的权重函数w(·)的差异也会减小，其中w(Pxi，Pxj，r)=(r-‖Pxj-Pxi‖)2。h(Pxi，Pxj)表示边特征，是该网络架构中最重要特征的提取部分。在3D欧式空间中，向量可以表示为3个正交基的投影，投影的模长表示在对应方向上的“能量”，因而可将边特征投影到3个正交基上，使用不同的权值矩阵提取各个方向的边特征，再将3个方向的特征重新聚合以维持欧式几何结构。基于极坐标的边特征计算公式如下：

(5)

其中，D表示Pxi与Pxj所在的象限的三个正交基的集合；Md表示与方向相关的权值矩阵，用来提取不同方向的边缘特征；cos2(Pθ)为系数，用以保证特征聚合时其和为1。

2 网络原型设计与精简

根据网络轻量化的原则，在PointNet的基础上，设计网络结构原型如图2所示。

通过简化网络结构，使网络仅包含基本的卷积层、池化层和全连接层，实现网络轻量化。为提取到点云的全局特征，采用最大池化层进行特征提取，设置卷积核大小为1×1。由于全连接层的每一个点都与上一层的所有点相连，综合了前几层的特征，因而全连接层的参数个数在整个网络架构中最多，对全连接层参数个数和节点数的精简是实现网络轻量化的重要步骤。在网络优化过程中，为探究某一层的参数对网络性能的影响，可保持其他层的参数与网络原型一致。

本实验以ModelNet40为基础数据集，通过以下流程确定网络结构和参数。

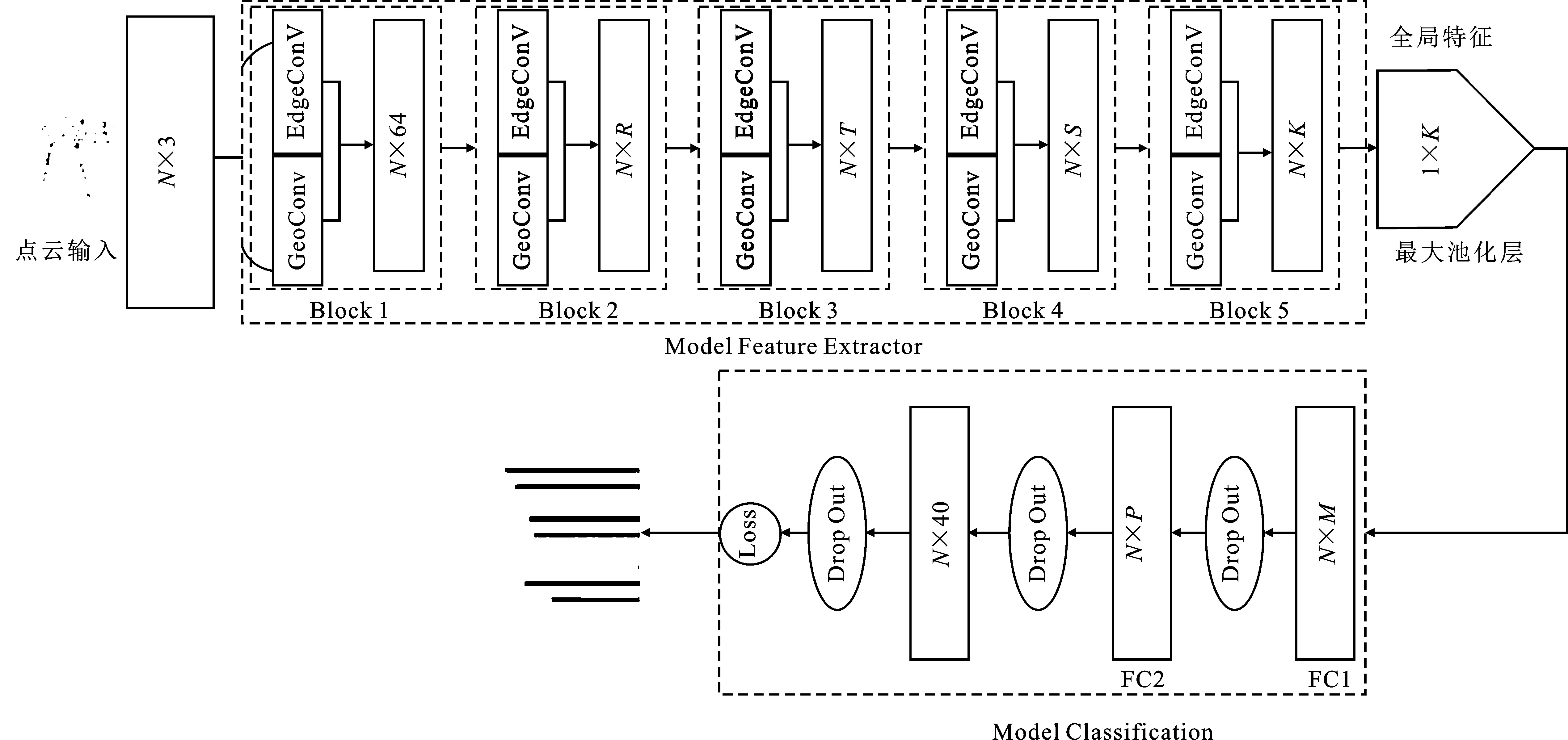
图2 网络结构原型

2.1 确定网络敏感层及卷积层个数和通道数

为精简网络结构，减少网络参数，去除了空间转换网络(STN)。设定R、T、S、K、M和P分别为64、64、128、1 024、512和256，得到原型实验结果。首先固定全连接层节点参数，调整T，S，K，M及P的参数值进行测试，实验共分为4组(表1)。第1组G1用来测试网络敏感层与非敏感层，通过逐步降低T和S的取值，分析实验结果的准确率，发现T和S的取值对网络整体性能影响很小，如图3所示。

由式(6)得出，IEGCNN网络通过多个卷积层计算h的值，τ的值由单个特征融合及最大池化操作计算，f的大小则与最大池化层和全连接层数量相关。通过逐层增加卷积层通道数实现对特征的深层提取。首层通道数的大小决定了整个网络模型通道数的设置。这意味着首层卷积层、池化层和全连接层是网络模型中的敏感层，直接影响着模型的整体性能。Block 3和Block 4在整个模型中的位置不与输入层和最大池化层直接相连，其改变对网络的整体性能影响不大，因而推断其为非敏感层。实验结果也验证了推论的合理性。

经过测试，精简模型能达到与网络原型相当的分类效果，在ModelNet40数据集上，训练42 min(0.7 h)时，准确率已趋于稳定，如图4所示。

图3 网络原型中的非敏感层测试图

2.2 确定全连接层个数和节点数

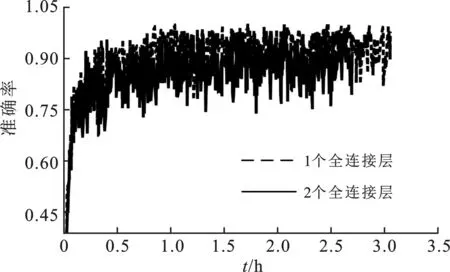
图5 全连接层数量与分类准确率关系

全连接层在整个网络中包含的参数最多，耗费更多的GPU资源。在卷积层确定后，通过调整全连接层个数和参数以确定最佳结构。首先确定全连接层的个数，通过对表1中G2组No.4与No.5、G1组No.3与G3组No.7进行分析，当全连接架构层数取1层时的分类准确率高于取2层时。图5为全连接架构分别为2层和1层的分类准确率变化曲线，因而确定全连接层为1层。其次，确定全连接层取不同参数时网络在训练集上的分类准确率。

由表1中第4组数据G4可以看出，固定其他参数，K过小，网络不能有效地拟合训练数据；当通道数达到固定值后，再增加通道数并不能带来新的性能提升，反而会造成网络参数量的快速增加，当K的取值与采样点的个数保持一致时分类效果最佳，故设置K为1 024，如图6所示。

表1 参数取值与分类结果(ModelNet40数据集)

图6 参数K与分类准确率关系

2.3 确定第1层、第2层卷积通道数

该模型输入的点云为欧氏空间中点的子集，采用多层卷积对点云特征提取的过程，就是逐层抽象，不断精炼知识的过程。通道数可以让每一层学习到更加丰富的特征，其带来的计算量是呈平方数增长的。对于任意一个模型来讲，浅层的通道数是一个非常敏感的系数，涉及到后续卷积层通道数的设置。首层通道数如果设置过小，特征的捕获能力将大幅下降，单纯增加网络深度会导致梯度弥散或梯度爆炸，而通道数的增加会带来计算量呈平方数的增长。

对第1层卷积层的通道数进行实验后发现，当通道数取值为64时效果最佳，取值32时分类性能较弱，取值128和256时分类性能不再提升。

第2层卷积层位于两个卷积层之间，不与输入层及池化层直接连接。为使点云特征维度逐步增大，架构中各个卷积层通道数采取逐步增大的方式进行，第2层的通道数设置应大于等于第一层通道数，小于等于第3层通道数。在该网络框架中，通过网络架构精简操作，去掉了第3、4层卷积层，第2层直接与第五层 Block 5 卷积层相连，因而第2层的通道数应设置为64与1 024之间。通过实验数据分析，准确率Accuracy的值随R的变化呈现出正态分布规律，当R取值为128时，Accuracy达到最大值，这也符合点云特征提取过程中特征维度递增的规律。从表1中G3组数据No.6至No.9，G4组数据No.13可以得出，当R取128时，分类准确率最高，如图7所示。

图7 参数R与分类准确率关系

2.4 设置索引跳跃链接

该网络架构以模块化方式处理点云数据，根据不同块之间的几何位置关系将特征进行合并及传递。本文提出一种索引跳跃链接(Index Hop Link，IHL)来记录各个层的位置信息，根据索引信息将不同层的输出特征映射并进行跳跃连接。为使网络对点云输入数据保证排列不变性，采用对称函数方法，具体定义为

f(Px1，Px2，…，Pxn)=μ·λ·d·τ(h1(G1)，h2(G2)，…，hn(Gn)，…hN(GN)) ，

(6)

其中，Pxn表示原始输入的点云，μ表示对特征通道融合，λ表示最大池化操作，d表示进行dropout操作，τ表示全连接操作；Gn表示第n层的特征输出，GN表示网络特征提取层的最后一层，Gn与GN在模型大小和排序方式上是不同的，通过hn进行索引、排序以及池化操作。

2.5 模型损失函数

网络模型采用交叉熵(CrossEntropy Loss)计算损失函数，它主要用来度量同一个随机变量中两个不同概率分布间的差异性，即真实概率分布与预测概率分布之间的差异。交叉熵值越小，说明模型的预测效果越好。交叉熵H(p，q)定义如下：

(7)

其中，p(x)表示样本的真实分布；q(x)表示模型的预测分布，可以通过反复训练q(x)，使得q(x)的分布逼近真实分布p(x)。

2.6 模型优化方法

采用Adam法(Adaptive moment estimation)进行优化。该方法对每个参数梯度的一阶矩阵估计和二阶矩阵估计动态调整每个参数的学习率，利用动量和自适应学习率来加快收敛速度；经过偏置校正后，每一次迭代学习率都有确定范围，模型参数规模稳定。

综上所述，笔者构造的索引边缘几何卷积神经网络IEGCNN模型结构如图8(a)所示，共包含5层。

(1) 输入层： 网络输入数据为包含有n个点的点云数据，表示为一个N×3的矩阵。

(2) 卷积层：包括Block 1、Block 2和Block 3，共3层。第1层为(64，3，1)，其中，64表示通道数，卷积核尺寸为1×3，步长为1×1；第2层为(128，1，1)；第3层为(1 024，1，1)。

(3) 池化层：位于第三层卷积之后，采用最大池化，得到一个1×1 024维的张量。

(4) 全连接层：以1×1 024维的张量为输入，通过全连接层得到1×256维度张量输出，为防止过拟合，在该池化层后加入DropOut层并设置大小为0.5。

(5) 输出层：k维的输出层和损失层(k表示输出类的个数)，将模型分类结果进行输出。

由于点云数据中每个点均由三维坐标(x，y，z)构成，相邻点之间的关系是随机的，没有确切的关联，因此，将步长设置为1×1以保持点间关系的独立性。

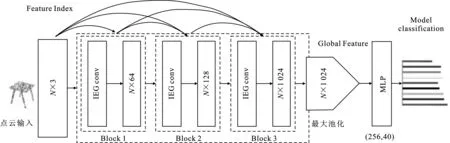
(a) 模型结构

(b) 向量分解

图8(b)描述了在三维坐标系中通过向量分解对点之间的几何结构进行建模的过程。首先将边缘特征沿3个正交方向分解，采用与方向相关的权重来提取方向信息，然后根据向量的方向对其进行聚合，构造点Pxi和点Pxj之间的边缘特征，再通过聚合函数f(p| (l))计算p点在l层的特征向量。

根据模型结构，计算IEGCNN网络的参数量，如表2所示。其中，n表示三维点的个数，k表示模型分类的个数。包括偏置项在内，共有(404 096+257k)个参数，在ModelNet40上约为0.61 M，在ModelNet10上约为0.41 M，其参数的数量和点云的输入规模n没有直接关系。该网络具有较好的鲁棒性，能适应不同规模的点云数据。此外，该模型的训练时间与输入点云的规模为线性关系，区别于MVCNN[15]网络对应的二次方增长和体素方法[17]随尺寸的三次方增长。

表2 IEGCNN参数量计算

通过索引特征传递，使当前索引从前一层的特性中提取新特性，结合前一层的特征计算边缘，可以有效避免深度神经网络的梯度消失和梯度爆炸的问题，从而得到信息丰富的边缘向量。

目前，处理点云的方法采用ModelNet40或ModelNet10数据集最为普遍。该模型直接处理点云数据，对点云的采样过程借鉴了PointNet，不同的是在特征提取过程中通过加入点的方向信息，引入索引边缘卷积的方法，使特征提取更加充分。通过表1的多组实验可以看出，所确定的模型参数在4组的实验过程中均取得最佳表现，在处理ModelNet点云过程中具有较好的普适性。该模型使用k近邻方式采样，模型参数在KITTI、SEMANTIC3D、D3DIS等实景数据集中普适性较弱；具体原因在结论部分进行说明。

3 实验结果与分析

3.1 实验环境

笔者选择ModelNet作为分类实验数据集。ModelNet是Princeton大学公开的三维模型分类标准数据集，共有662类12 715个分类模型，分为ModelNet10和ModelNet40两类。ModelNet10包含10类共4 899个模型，其中3 991个训练样本和908个测试样本；ModelNet40包含40类共12 311个模型，其中9 843个用于训练模型，2 468个用于测试。使用该类划分方式进行测试的结果称为实例准确率。如果将每个类别测试目录前20个模型作为测试集，训练目录前80个作为训练集进行划分测试，则其测试结果称之为类别准确率。本实验选取实例准确率为测试结果。

本实验的硬件环境为Intel Core i9-9900k CPU+GTX2080Ti (11GB显存)GPU，软件环境为Ubuntu18.04+CUDA 10.0.130+cuDNN7.4.2+Tensorflow1.13.2+Python2.7。实验过程中，设置采样点数为1 024，batch_size为16，learning_rate为0.001，momentum默认值为0.9，decay_rate为0.7；为方便与其他网络架构进行对比，设置最大迭代次数max_epoch为默认的250次。

3.2 实验结果分析比较

表3为不同模型分类方法的比较，下划线“_”标记数据的为参考文献作者测试的分类结果，波浪线“～”表示近似值。文中方法在ModelNet40上取得了约92.78%的分类准确率(表中用粗体字表示)，在ModelNet10上的分类准确率约为94.2%(表中用粗体字表示)，参数个数为0.61M，在同等参数个数情况下，取得了最好的成绩。高于所有的基于多视图分类网络和大部分基于体素和点云的分类网络。以下对实验结果进行分析和讨论：

1) 与基于多视图融合网络比较

基于多视图融合的方法利用多个不同固定视角的投影将渲染图输入到卷积神经网络中，卷积神经网络从投影渲染图中进行单视角特征提取，输入要求为连续模型。而文中的IEGCNN网络模型以稀疏、无序的点云作为输入，网络模型更加轻量化，参数仅约占基于Multi-view的0.4%，在ModelNet40和ModelNet10上分类准确率分别比Pairwise网络提高了约2.08%和1.4%，这说明IEGCNN能很好地学习点云模型的本质特征。

2) 与基于体素网络比较

基于体素的网络由于发挥了深度学习的优势，网络层数可以搭建得更深，网络结构可以更加复杂，体素化实现了在三维模型上直接做卷积与池化操作，但是限于分辨率的问题，会丢失三维模型的局部细节，卷积操作所消耗的时间资源更多。笔者提出的方法分类准确率仅比众多体素方法中的VRN Ensemble低，在ModelNet40和ModelNet10数据集上分类准确率分别下降了约2.76%和2.94%。

VRN Ensemble训练基于体素的可变自动编码器，该网络在ResNet的基础上进行设计，深层的ResNet可以看做是不同深度的浅层神经网络的集成，ResNet通过跳跃连接，增强了梯度的流动。基于体素的网络充分发挥了深度学习的优势。该网络层数深达45层，网络架构复杂，随着深度的增加，网络可以通过许多非线性映射和改进的特征表示来更好地近似目标函数。综合以上原因，基于VRN Ensemble的网络分类准确率高于文中方法，但该网络训练中需要对三维体素模型进行编码和解码操作，训练时间最长，需要 6天。同时，基于体素的深度学习网络均无法直接应用于无序、稀疏的点云模型，需要繁杂的体素化操作。笔者设计的网络模型仅包含3层卷积层和一个全连接层，可以快速地直接处理点云。网络参数约占VRN Ensemble方法的0.7%。文中方法卷积层为3层，VRN架构的卷积层为45层，在轻量级和实时性方面均占有优势。

3) 与PointNet的比较

笔者设计的网络架构，网络参数约占PointNet的1%。使用ModelNet40和ModelNet10数据集，分类准确率分别提高了约3.58%和1.12%。IEGCNN比PointNet(Vanilla)的网络参数约降低了0.19 M，但分类性能在ModelNet40和ModelNet10上分别提升了约5.58%和2.24%。实验结果表明，本网络架构在以原始点云作为输入的网络中，能满足分类准确率和轻量化的需求。

4) 与LDGCNN和DGCNN的比较

IEGCNN相比DGCNN的分类准确率提高了约0.58%，网络参数约占DGCNN的30%。虽然在ModelNet40上分类准确率比LDGCNN模型约低0.12%，但卷积层个数约占LDGCNN的60%，训练时间约为LDGCNN模型的1/3。所以，单纯地增加通道数量和全连结层的个数，并不一定能提高网络架构的整体性能。

5) 与3DmFV和Point2Sequences网络的比较

3DmFV把费舍尔向量作为卷积神经网络的输入，将点云体素化为标准的三维网格，解决了点云的无序性问题。由于费舍尔向量在计算的时候使用体素化网格，其计算量大，内存消耗也大，通过人工特征提取的方式，会导致信息的损失。Point2Sequences是一种基于循环神经网络的模型，采用一种点云序列学习模型，通过捕获点云局部区域内不同区域之间的相关性，将所有局部区域的特征输入到一个循环神经网络的编码-解码器中，实现区域特征的聚合。笔者提出的IEGCNN网络在ModelNet40上，分类准确率比3DmFV 提高约1.68%，比Point2Sequences提高约0.18%，但是在ModelNet10上，比3DmFV和Point2Sequences分别降低了约1%和1.1%，原因是本架构舍弃掉了传统的特征转换层，卷积层个数、全连接层的个数和节点数大幅降低。在ModelNet10数据集中，由于训练样本和测试样本的分布模式、模型数量的限制，导致没有充分提取点云模型的特征。

表3 不同算法在ModelNet数据集上的分类结果

6) 精简模型普适性分析

该网络模型的框架基于PointNet设计，考虑到PointNet及PointNet++网络结构中局部特征提取不充分的问题，提出引入点的方向信息的方法，结合边缘索引跳跃链接，缩减网络规模，减少模型中卷积层的个数，逐步改变各个卷积层通道数量，确定最佳模型参数。网络结构的精简，从理论上，对分类准确率会造成一定降低。作为对卷积网络裁剪造成准确率降低的补偿，文中将第2层卷积层(Block 2)的通道数由原模型的64提升到128，优化特征提取流程，采用索引特征传递，使特征丢失减少，提取更加全面。由实验数据分析，精简后的网络模型能快速处理整个点云模型，在降低参数量的同时，分类精度有所提高，具有很强的普适性。

4 结束语

笔者提出一种层级特征提取框架来解决点之间局部几何结构建模的问题。通过分析PointNet、PointNet++及DGCNN等点云模型及其在局部特征提取方面的特点，提出索引边缘几何卷积神经网络IEGCNN，从每个点及其邻域提取特征，计算中心点和其邻域范围内点的距离，并在边缘卷积网络中加入点的方向信息，将边缘网络架构中点与点之间的关系投影到三维坐标系，并分解为3个正交基，根据边缘向量与基向量之间的夹角、中心点与邻域点的距离进行特征聚合，从而对两点之间的几何结构进行建模。IEGCNN将卷积层减少至3层，为每层的输出建立索引并传递至其他所有层，在同等规模参数量和通道数的网络架构中取得了最好的分类效果。在训练和识别时间上大幅缩短，具有快速处理点云数据的能力。该工作不仅在分类任务上取得了较好的效果，也为解决目标检测网络实时性问题提供了思路，在可移动设备部署及实时处理方面具有广阔的应用前景。实验中发现，笔者提出的方法存在以下不足：

(1) 使用的k近邻采样法，存在依赖训练样本，很难适应大规模数据集的问题，对k值的选择还需进一步优化。

(2) 笔者采用基于均匀采样的点云进行训练，而实际场景中的点云往往是疏密不同的，这会导致实际场景点云中准确率降低。这可通过动态调整局部区域采样点数量来优化。这都是需要继续研究的方向。