功率受限CR-NOMA协作V2X中断性能分析
2022-05-28乔宇航张良梅贺玉成
乔宇航,张良梅,贺玉成,2,周 林,2
(1.华侨大学 厦门市移动多媒体通信重点实验室,福建 厦门 361021;2.西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)
在高速发展的信息时代中,人们对移动通信提出了更高的需求,渴望更丰富的带宽资源。车联网(Vehicle to Everything,V2X)系统是实现万物互联的关键组成部分,然而在车辆拥堵或信息交互频繁的情况下,同一时间内巨量用户接入导致的信息拥堵将大幅提高资源碰撞的可能性。非正交多址(Non-Orthogonal Multiple Access,NOMA)技术在提高过载率,避免资源碰撞,满足V2X场景低时延高可靠性需求方面很有前景[1-2]。NOMA技术不再局限于资源的正交分配,而是通过引入可控干扰,以增加接收机的复杂度为代价,实现相同时频资源上的多用户通信[3]。此外,车辆高速移动导致的载波频率偏移(Carrier Frequency Offset,CFO)效应对NOMA影响较小,是NOMA技术应用于V2X网络的另一大技术优势[4]。
文献[5]将NOMA技术用于V2X网络以缓解资源拥堵,针对组播/广播NOMA-V2X网络考虑了全双工(Full Duplex,FD)和半双工(Half Duplex,HD)两种中继协作方案,并以最小化所有用户可达速率为标准,提出了一种基于二分法的最优功率分配策略。文献[6]提出了基于FD-NOMA的分散式V2X系统模型,分析并推导了系统容量的高精度近似表达式。文献[7]提出了一种适用于全双工NOMA-V2X网络的路边单元(Road-Side Unit,RSU)选择方案,将中继选择引入NOMA-V2X网络以提高系统遍历容量。目前,在大多数针对协作NOMA网络的研究中,功率分配策略通常取决于中继到用户的信道质量。文献[8]针对多中继协作NOMA网络,提出根据用户服务质量(Quality of Service,QoS)需求决定功率分配与串行干扰消除(Successive Interference Cancellation,SIC)顺序,研究了信道质量较差用户的中断性能,并推导了其中断概率的闭式解。文献[9]针对多中继协作NOMA网络,分别推导了两阶段中继选择(Two-Stage Relay Selection,TSRS)和最大-最小(max-min)中继选择下两NOMA用户中断概率的闭式解,证明了TSRS方案在改善用户中断性能方面的优越性。
为次级用户提供动态频谱接入的认知无线电(Cognitive Radio,CR)是另一种在提高频谱效率方面有前景的技术[10]。已有研究表明,NOMA技术与CR体制的结合(CR-NOMA),可极大提高接入主用户(Primary User,PU)频谱的次级用户(Secondary User,SU)数量,从而大幅提升系统吞吐量[11]。未来存在大量潜在活动设备且可互为中继的增强型车联网(Enhanced V2X,E-V2X)将是协作CR-NOMA技术主要应用场景之一。因为对潜在活动设备而言,固定的频谱授权方式会导致频谱资源利用率低下。文献[12]针对底层模式的协作认知NOMA网络,考虑了次级网络中继与用户无法利用SIC将多址干扰理想消除的情况,对此推导了两个次级用户中断概率的精确解,并通过渐近分析获得了次级网络源节点发射功率与噪声温度限(Interference Temperature Constraint,ITC)无限大时次级用户中断概率的渐近表达式。文献[13]针对存在两个次级用户的单中继协作CR-NOMA网络,考虑近用户充当远用户的全双工/半双工解码转发中继,在近用户最大发射功率受ITC约束下,推导了FD-CR-NOMA网络远用户中断概率的解析式。
此外,对于能量开销依赖于电池储备的传统中继设备,能够实现持续充能的无线携能通信(Simultaneous Wireless Information and Power Transfer,SWIPT)技术可有效延长其电池使用寿命[14]。另一方面,已有研究表明,能够同时进行无线信息与能量传输的SWIPT技术可有效提高通信系统的频谱效率[15]。SWIPT的技术特点使其在能量效率与服务质量要求严格的NOMA-V2X网络中具有极大的应用前景。文献[16]针对多中继协作SWIPT-CR-NOMA网络,研究了主网络空闲状态时的次级用户中断性能,在保证主网络用户所受干扰在可接受范围的基础上,推导了TSRS方案下两个次级用户中断概率的闭式解。文献[17]研究了NOMA技术在支持同步无线信息与能量传输的单中继协作认知网络中的应用,推导了系统中断概率与两个次级用户中断概率的精确表达式。研究结果表明,与OMA相比,NOMA技术可以提高采用SWIPT的协作认知网络中断性能,但SU中断概率依旧较高。在文献[17]的基础上,文献[18]假设次级网络中继与用户均受到来自主网络源节点的白噪声干扰,并基于此假设推导了各次级用户中断概率的精确解。
笔者将NOMA技术应用于V2X系统,研究了采用SWIPT技术的多中继协作认知NOMA-V2X网络在TSRS方案下的中断性能。与文献[16]未考虑主网络源节点不同,笔者考虑主网络源节点处于非静默状态。具体表现为:认知中继同时接收来自次级网络源节点的叠加信号与主网络源节点的干扰信号,使用功率分裂的SWIPT协议从两个信号中采集能量。最优中继在主网络信号干扰下解码次级网络源节点广播的叠加信号,并仅利用采集自主次网络源节点的能量,向所有次级用户转发再编码信号。推导了两次级用户在主网络信号干扰情况下的中断概率近似解。结果表明,与同样考虑SWIPT-CR-NOMA网络中主网络干扰的文献[18]方案相比,在次级用户中断性能方面,笔者提出的方案更优。
1 系统模型
系统设计考虑更为切合实际的场景,即主网络处于非空闲状态时,利用底层CR技术为SU提供机会式通信,通过中继选择来搭建最优两阶段中继链路,既要满足信道质量较差用户的特定目标速率,又要为信道质量较好用户提供尽可能大的传输速率。
系统模型如图1所示,由主网络和次级网络两部分构成:主网络包括拥有授权频谱的一个源节点PS和一个用户车辆PU,均为单天线配置;次级网络包括在同一频谱进行机会式通信的一个源节点S、N个半双工中继车辆Rn(n∈{1,2,…,N})和两个用户车辆Ui(i∈{1,2}),共计N+3个单天线设备。由于深度衰落或建筑阻碍,S必须在中继协助下才能与Ui通信,其中Rn采用功率分裂的SWIPT协议采集并存储能量,且在第一次执行SWIPT前无能量存储。所有信道均建模为统计无关的非频选Rayleigh衰落信道,信道系数可表示为hjk~CN(0,λjk)(jk∈{SP,SRn,RnP,RnUi,PRn,PUi})。为方便计算,假定Rn与Ui具有统计特征相同(均值为0、方差为σ2)的加性复高斯白噪声。每个通信过程包括如下两个时隙。

图1 系统模型
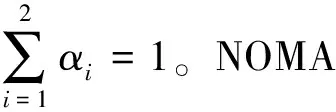
(1)

Rn对接收信号功率按照能量分裂参数ω∈[0,1]进行分割,部分用于信息解码,其余用于能量采集,用于信息解码的信号可表示为
(2)
其中,nRn为Rn的加性复高斯白噪声。
SIC算法按照功率分配降序对各信号分量逐次判决和消除,因此Rn依次检测信号x1与x2的信干噪比可相应表示为
(3)
(4)
其中,ρS=PS/σ2,ρP=PP/σ2。
根据SWIPT协议,Rn可采集的能量表示为
(5)
其中,η表示能量采集效率,0<η<1,由于接收噪声nRn强度过小,式(5)忽略了从中采集的能量。
为简化推导,不考虑编译码电路的能量消耗,由式(5)可推得Rn的可达转发功率峰值:
(6)
并根据式(1),式(6)改写为
(7)
第二时隙,Rn在成功解码各个用户信号的前提下,生成再编码叠加信号(PRnα1)1/2x1+(PRnα2)1/2x2向Ui转发,其中PRn为Rn在干扰温度限约束下的实际发射功率:
(8)
Ui接收信号来自主次网络两个源节点(主网络源节点信号为干扰信号),可表示为
(9)
其中,nUi为Ui处的加性复高斯白噪声。
为采用SIC技术,U1与U2均需首先检测发射功率较大的信号x1,相应的信干噪比可统一表示为
(10)
其中,ρRn=PRn/σ2。

(11)
根据系统设计思想以及上述公式,TSRS方案的设计分为如下两步:
(1) 构建中继子集Sr:其成员能够成功检测信号x1和x2、并保证U1与U2亦能成功检测信号x1,在所有中继已知全局信道状态信息的前提下,Sr可表示为
Sr={Rn:En,1≤n≤N} ,
(12)
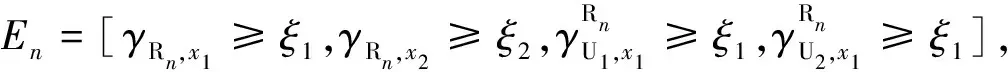
(2) 最优中继选择:当Sr非空集时,以最大化U2传输速率为准则,在Sr中挑选最优中继Rn*为
(13)

2 中断概率公式推导
当用户无法接收到自身期望信号,或无法自接收信号中成功解码自身期望信号时,用户发生中断事件。由TSRS方案的设计步骤(1)可知,U1仅当无中继提供转发服务即Sr为空集时发生中断。由式(12)和式(13)可知,U2在两种情况下发生中断:第一种情况与U1相同,即|Sr|=0;第二种情况为U2无法从Rn*转发信号中成功检测信号x2,即|Sr|>0且γn*<ξ2。
假定N个中继紧密聚集,同一源节点或用户节点到不同中继的信道相互独立且统计特征相同,即λSRn=λSR,λRnU1=λRU1,λRnU2=λRU2,λRnP=λRP,λPRn=λPR,可推得如下定理1和定理2。
定理1U1的中断概率为
(14)
其中,P1=P{En},表示任一中继Rn属于Sr的概率。最终推得
(15)
其中,函数fX1n(t)、fX2n(t)、f1(t)、f2(t)分别由式(32)、式(33)、式(43)给出(证明见附录A)。
定理2U2的中断概率为
(16)
其中,P2表示U2可从接收的Rn*再编码信号中成功解码信号x2的概率,最终推导得出
(17)
其中,函数f3(t)和f4(t)分别由式(47)和式(48)给出(证明见附录B)。
上述P1和P2的表达式中所使用的中间变量由变量组列出。
变量组1:计算P1和P2的中间变量。
κ1=ξ1/(α1-ξ1α2)(1-ω),μ1=ξ1/(α1-ξ1α2) ,
κ2=ξ2/α2(1-ω) ,μ2=ξ2/α2,
κ3=max{κ1,κ2} ,μ3=max{μ1,μ2} ,
φ=ηω,ρQ=Q/σ2,
3 数值结果与分析

图3给出功率分配因子α1对Ui中断概率影响的仿真结果。由式(3)、式(4)、式(12)可推出,当α1≤ξ1α2时,所有中继均无法成功检测信号x1,两种方案下Ui均必然发生中断,因此图3中每条曲线的左侧均存在一个临界点α1≤ξ1/(1+ξ1)=1-2-2R1=0.67。当α1>ξ1α2=0.67时,随着α1的增大,两种方案下Ui中断概率均表现为先减后增。这是因为中继使用SIC技术时,其提供解码转发服务的前提为成功检测所有信号,而增大α1会在提高Rn检测x1成功率的同时也提高Rn检测x2的失败率,因此,Ui中断概率存在极小值。另一方面,TSRS方案下Ui中断概率受α1影响较文献[18]的更大。
图4给出能量分裂参数ω对Ui中断概率影响的仿真结果。首先可以观察到,Ui中断概率在ω=0与ω=1时均为1,这是因为在功率分割SWIPT协议中,信息解码与采集能量任一部分能量为0均会导致Rn无法向Ui转发叠加信号。在图示区间内,TSRS方案下Ui中断概率较文献[18]体制下波动更大,但整体趋势均为先减后增。因为ω的增大虽然会提高中继转发再编码信号的发射功率峰值,但同样会降低中继成功解码所有用户信号的概率,因此存在最优能量分裂参数进行性能折中,但使不同用户达到最优性能的ω不同。在上述默认参数设置下,在选择最优ω时,TSRS方案较文献[18]可将Ui中断性能提升10~20 dB。
图5给出TSRS方案下Ui中断概率与中继规模N的关系曲线。可以发现,N对Ui中断概率影响巨大,Ui中断概率随N的增大而线性降低。因此TSRS方案下提高可供选择的中继数量是提升Ui中断性能的有效方法,但对不同用户中断性能提升效果存在差异。在笔者设置的参数下,U1中断性能提升较大。

图4 Ui中断概率与ω的关系曲线

图6 Ui中断概率与ρQ的关系曲线

4 总 结
笔者研究了两阶段中继选择方案在联合无线携能传输与中继选择的底层认知NOMA-V2X网络中的应用,考虑了主网络干扰下的两次级用户场景,对两次级用户中断概率近似表达式进行了推导。研究结果表明,在参数设置合理的情况下,文中方案可将次级用户中断概率在现有方案(如文献[18])的基础上降低10 dB以上。另一方面,在上述默认仿真参数下,提升可供选择的中继数量是提升系统中断性能的有效手段,在未来车队编排等存在大量中继机会的场景中,笔者提出的方案具有实际应用价值。
附录A
由中继信道模型可知任一中继Rn∈Sr的概率P{En}均相等,记为P1=P{En},因此用户U1的中断概率由式(14)的第一个等式可改写为
(18)
根据式(3)、式(4)、式(10)和式(12),可将En整理为(中间变量如变量组1所示):
(19)
(20)
(21)
(22)

(23)
(24)
由式(19)、式(23)和式(24)整理得Δ11、Δ12、Δ21和Δ22为
(25)
(26)
(27)
(28)
(29)
由式(22)分别推导X1n和X2n的概率分布函数为
(30)
(31)
其中,Ei(x)为指数积分函数[19],中间变量如变量组2所示。
进一步可推得X1n和X2n的概率密度函数为
(32)
(33)
其中的中间变量如变量组3所示。
式(25)~式(28)中Δ11、Δ12、Δ21和Δ22的积分表达式为
(34)
(35)
(36)
(37)
式(34)~式(37)的积分难以获得准确解,根据Gauss-Chebyshev求积公式[20],可将其近似为
(38)
(39)
(40)
(41)
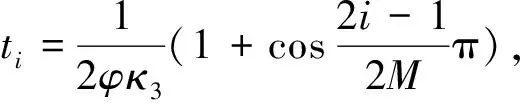
(42)
(43)
附录B
当|Sr|=0时,式(16)的第一项已由定理1推得;当|Sr|>0时,式(16)的第二项由中继信道的独立同分布假设可推得为
(44)
其中,P{γn<ξ2|En}为Sr中任一成员无法使U2成功检测信号x2的概率,由式(13)推导如下:
1-P{E′n}/P{En}=1-P2/P1,
(45)

P2的推导与P1类似,根据式(46)最终可推得P2表达式为式(17),其中f3(t)和f4(t)的表达式为
(47)
(48)
其中,计算f3(t)和f4(t)的中间变量如变量组4所示。
变量组2:计算FX1n(t)和FX2n(t)的中间变量。

a5=φρP(μ3+1) ,
b1=(ρQλSR/μ3ρPλSPλPR)exp[(κ3λSP+ρQλSR)/μ3ρPλPRλSP] ,
b5=(ρQλSR/ρPλSPλPR)exp[-ρQλSR/ρPλSPλPR] ,

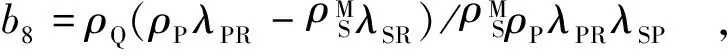
b10=μ3/φρP(μ3+1) ,b11=ρQλSR/ρPλSP+κ3/ρP(μ3+1) ,

b14=1/φρP,b15=ρQλSR/ρPλSP。
变量组3:计算fX1n(t)和fX2n(t)的中间变量。
c1=(a1/φa3)exp[(a1a2-a3)κ3/a1a3]+(a1a2/φa3a4)exp[-a4κ3/a3] ,
c2=a2/φa3,c3=1/φa1,
c4=1/φa4,c5=-(a1/φa3)exp[a2κ3/a3-κ3/a1] ,
c6=1/φa1a5,c7=κ3/a1a5,
c8=1/a5,d1=b1b2eb3-b4,
d2=b3-b4,d3=b5b6,
d4=b9b10,d5=b9b11,
d6=b5b7e-b8,d7=b6+b7,
d8=b5b9b10e-b9b11,d9=b6+b9b10。
变量组4:计算f1(t)、f2(t)、f3(t)和f4(t)的中间变量。
θ1=μ1ρPλPU1/λRU1,θ2=μ1ρPλPU2/λRU2,
θ3=μ1(λRU1+λRU2)/λRU1λRU2,θ4=ρQλRU1/μ1ρPλPU1,
θ5=ρQλRU2/μ1ρPλPU2,
θ6=(μ1(λRU2+λRU1)λRP+ρQλRU1λRU2)/ρQλRU1λRU2λRP,
θ7=(μ1λRU2+μ3λRU1)/λRU1λRU2,θ8=μ3ρPλPU2/λRU2,
θ9=ρQλRU2/μ3ρPλPU2,
θ10=((μ1λRU2+μ3λRU1)λRP+ρQλRU1λRU2)/ρQλRU1λRU2λRP。
