一种新的传感器节点分布式定位算法

徐莎莎，周 芳，李杨剑，蒋俊正，3

(1.桂林电子科技大学 信息与通信学院，广西壮族自治区 桂林 541004；2.桂林电子科技大学 生命与环境科学学院，广西壮族自治区 桂林 541004；3.桂林电子科技大学 广西无线宽带通信与信号处理重点实验室，广西壮族自治区 桂林 541004)

无线传感器网络(Wireless Sensor Networks，WSN)是由大量微小的传感器构成的自组织网络[1]。无线传感器网络中传感器节点可以检测监控区域中的物理信息并进行数据处理，并将处理后的数据以无线通信的方式传送到基站[1]。无线传感器网络有许多应用，如医学应用中的病人检测[2]，环境应用中火山检测[3]，家庭应用中用水检测等[4]。在上述广泛应用中，检测到的信息需要与传感器节点的位置结合起来，才能提供更有效的数据信息。因此，可以在传感器中嵌入中国北斗卫星导航系统(BeiDou navigation Satellite System，BDS)模块或全球定位系统(Global Positioning System，GPS)模块。但这些模块成本高，功耗大，无法适用于大规模的无线传感器网络。因此，选择少量的传感器节点嵌入中国北斗卫星导航系统或全球定位系统模块，这些传感器节点称为锚节点或已知位置(Location-Aware，LA)节点，可以获得较精确的位置信息，其他传感器节点则称为未知位置(Location-Unaware，LU)节点[5]。之后采用测距技术，如接收信号强度(Received-Signal-Strength，RSS)、到达时间(Time-Of-Arrival，TOA)、到达角(Angle-Of-Arrival，AOA)等测得无线传感器网络中传感器节点之间的距离[5]。然后使用定位算法估计出无线传感器网络中LU节点的位置。

目前，已有很多定位算法被提出。从数据处理角度，可以将定位算法分为集中式定位算法和分布式定位算法。集中式定位算法将定位所需信息通过多跳的方式传递给存储、计算能力较强的中央处理器进行处理。文献[5]将定位问题归结为无约束的优化问题，并采用修正牛顿法进行求解，得到了较好的定位精度和定位速率。但该算法计算复杂度较高。文献[6]提出了一种集中式定位算法，将定位问题采用半正定规划松弛的方法进行求解，将结果作为初始值，进而采用梯度下降法得出LU节点的位置，提高了定位精度。总之，集中式定位算法使用了全部的定位信息，定位精度较高，但通信代价也较高。离中央处理器较近的传感器需要传输大量的信息，会较早地消耗完电量，导致整个无线传感器网络无法工作。而且，集中式定位算法计算复杂度较高，导致扩展性较低，无法在大规模无线传感器网络中使用。而分布式定位算法使用传感器节点自带的处理器，对收集到的局部信息进行处理，有效降低了通信代价和计算复杂度，具备良好的扩展性，可用于大规模无线传感器网络。文献[7]将非凸的定位问题松弛为凸的二阶锥规划问题，利用LU节点及其邻居信息，设计分布式二阶锥规划定位算法进行求解。该算法可用于大规模无线传感器网络中，但定位精度较低。文献[8]提出了一种分布式定位算法，在每个LU节点上，将非凸的定位问题松弛为凸的定位问题，并使用梯度法进行求解，在通信半径较小的情况下也有较好的定位效果，降低了通信代价。但该算法需要将LU节点部署在LA节点的凸包中，才能有好的定位精度。文献[9]将无线传感器网络划分为子图，每个子图满足提出的刚性条件，用多维标度算法对每个子图定位，再将局部坐标映射到全局坐标系统。该算法所需的LA节点数目较少，且划分的子图数目较少，定位精度较高。但当通信半径较小，子图无法满足刚性条件时，无法定位。文献[10]提出了一种基于超级节点的分布式传感器节点定位算法，该算法将LA节点作为超级节点，对无线传感器网络进行子图划分，并进行求解。该算法有较好的定位精度，但该划分方法难以保证划分的子图能覆盖所有节点。

为了使定位算法有较高的扩展性和定位精度，能够有效用于大规模无线传感器网络中，笔者提出了一种新的分布式定位算法。首先将无线传感器网络看作一个图模型，将整个图分解为部分重叠的子图，进而将定位问题分解为一系列子图中的优化问题。然后提出一种分布式定位算法，迭代地求解LU节点位置。每次迭代包含两个关键步骤：一是LU节点位置估计，使用Barzilai-Borwein梯度法求解子图中小规模优化问题，得到子图中LU节点的估计位置；二是子图融合，对部分重叠的子图进行融合，从而得到LU节点的估计位置。笔者所提算法与集中式定位算法相比，有近似的定位精度，并通过对算法计算复杂度分析，表明这种算法计算复杂度更低，可用于大规模无线传感器网络中。与分布式定位算法相比，笔者提出的算法有更高的定位精度，而且对部署区域边界的LU节点也有较好的定位效果。

1 定位问题的描述

1.1 图模型

无线传感器网络是自组织网络，可以通过无向图G=(V，E)来描述。其中，V=V1∪V2，V1={1，2，3，…，n}表示无线传感器网络中LU节点集合；V2={1，2，3，…，m}表示无线传感器网络中LA节点集合；E={eiλ，eij}，(i=1，2，3，…，n；j=1，2，3，…，n；λ=1，2，3，…，m)表示节点之间边的集合。其中，eiλ表示LU节点i与LA节点λ之间可以直接通信；eij表示LU节点i和LU节点j之间可以直接通信。由于受到传感器节点功率的限制，传感器节点只能与通信半径R内的节点直接通信。这样可以将无线传感器网络构成的无向图划分为部分重叠的子图，采用以LU节点为中心将WSN划分为部分重叠的子图：

(1)

Gs=(Vs，Es) ，

(2)

图1 子图分解示意图

其中，Vs=Vs1∪Vs2，Vs1表示子图Gs中LU节点的集合，Vs2表示子图Gs中LA节点集合，Es表示子图Gs中节点之间边的集合。如图1所示，传感器节点分布在[-0.5，0.5]2单位区域内，其中，圆圈表示LU节点，实心菱形表示LA节点，虚线圆表示以LU节点为圆心，R为半径，划分出的部分重叠的子图。

1.2 定位问题的归结

在监控区域Rd(d≥1)维空间中部署大量的传感器节点，这些节点构成无线传感器网络。无线传感器网络中共有N个节点，其中有m个LA节点，n个LU节点。考虑传感器节点部署在d=2的二维欧几里得空间中。LA节点位置表示为aλ，λ=1，2，3，…，m；LU位置表示为xi，i=1，2，3，…，n。LU节点i与LU节点j之间的欧氏距离表示为dij，dij=dji[8]；LU节点i与LA节点λ之间的欧式距离表示为diλ。假设传感器节点的最大通信半径为R，则对于每个LU节点i定义两个集合：Ni={j，dij≤R，j=1，2，3，…，n}和Mi={λ，diλ≤R，λ=1，2，3，…，m}，其中Ni表示在通信半径R内，可以直接和节点i通信的LU节点邻居集合；Mi表示在通信半径R内，可以直接和节点i通信的LA节点邻居集合。定位问题可以描述为：利用m个LA节点的位置信息、节点的邻居信息和节点之间带噪声的距离信息，估计出n个LU节点xi(i=1，2，3，…，n)的位置。因此，WSN中节点定位问题可以归结为一个无约束的优化问题[5-6]：

(3)

其中，ωij和ωiλ是权重。因为dij和diλ是带噪声的测距，因此给可信度较高的测距设置较大的权重；反之，给可信度较低的测距设置较小的权重[5-6]。

2 分布式定位算法

2.1 子图内定位问题的描述

根据节1.1，将无线传感器网络构成的无向图以LU节点为中心划分为部分重叠的子图后，可以将定位问题式(3)近似地重新构造为

(4)

其中，Es为子图Gs中节点之间边的集合，dij和diλ分别为子图Gs中LU节点之间以及LU节点与LA节点之间的距离。使用RSS技术测得的距离包含噪声，噪声模型如式(5)、式(6)所示[6-8]。且LA节点即使加上GPS模块，由于受到电离层误差、对流层误差等多种误差的影响，得到的LA位置也是有噪声的，噪声模型如式(7)所示[7]。

dij=‖xi-xj‖2|1+τ1εij| ，

(5)

diλ=‖xi-aλ‖2|1+τ1εiλ| ，

(6)

(7)

式(4)中ωij和ωiλ是子图Gs中根据节点之间距离的反比取的归一化权重。两个节点之间相距越近，使用RSS技术测得的距离可信度越高[11]，应赋予较高权重，反之，应赋予较低权重[5，10]。权重分别为

(8)

(9)

(10)

(11)

其中，

A=(ei1-ej1)(ei1-ej1)T+(ei2-ej2)(ei2-ej2)T，

(12)

(13)

(14)

(15)

(16)

式(4)可以改写为

(17)

fs(x)的梯度向量∇fs(x)为

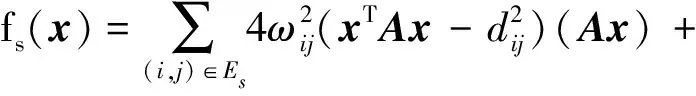
(18)

2.2 子图求解

2.2.1 初始定位

在获得WSN中节点之间测距信息后，采用简单的极大似然估计法获得LU节点的估计值[12]。目的是为了得到好的初始值。

假设D点为LU节点，坐标为(x，y)，在D点的通信半径R内有m个LA节点1，2，3，…，m，坐标分别为(x1，y1)，(x2，y2)，(x3，y3)，…，(xm，ym)。使用RSS测距法测得D点至m个LA节点的测距分别为d1，d2，d3，…，dm。则测得的距离与D点坐标和m个LA节点坐标之间有以下关系：

(19)

将前m-1个方程与第m个方程相减，得到以下方程组：

( 20)

式(20)可写为矩阵形式：

AX=b。

(21)

最小二乘解即为LU节点D的估计值：

(22)

在实际情况中，传感器节点随机部署，且受到通信半径R的限制，很难保证每个LU节点都有3个及以上的LA邻居。因此，笔者使用以下规则估计LU节点的初始位置：① 当LU节点有3个及以上的LA邻居时，使用最大似然估计法计算LU节点的初始位置；② 当LU节点有低于3个LA邻居时，将距离LU节点最近的LA节点的位置作为其初始位置；③ 当LU节点没有LA邻居时，将传感器节点分布区域的中心作为LU节点的初始位置，这样最大的初始定位误差为区域对角线的一半。

2.2.2Barzilai-Borwein梯度法

将无线传感器网络划分为部分重叠的子图后，子图中定位问题式(4)规模远小于原定位问题式(3)的规模，而且使用极大似然估计法可以得到较好的初始值。因此，可以用简单的梯度法进行优化求解，梯度法中步长的选择会影响收敛速度[13]。采用Barzilai-Borwein梯度法，不需要进行线性搜索，仅使用当前点和前一次迭代点的信息确定步长。在每次迭代中，只需要少量的存储和简单的梯度计算，降低了计算量。而且与传统的最速下降法相比，很大程度上加快了梯度法的收敛速度[13]。梯度法迭代公式如下：

xk+1=xk-αk∇f(xk) 。

(23)

可将上式写为

xk+1=xk-Fk∇f(xk) ，

(24)

其中，Fk=αkI。利用拟牛顿法割线方程的性质[14]，求解以下最小二乘问题：

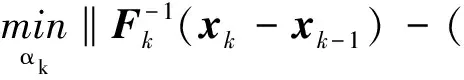
(25)

可以得到步长

(26)

如果k=0，则通过回溯直线搜索法确定步长α0，设置参数μ=0.2，β=0.5，α0=1，若下式成立，则令α0=βα0，继续循环，直到下式不成立：

fs(xk+α0Δxk)>fs(xk)+μα0∇fs(xk)TΔxk。

(27)

综上所述，子图中使用Barzilai-Borwein梯度法进行优化求解的步骤如下：

(1) 使用极大似然估计法，粗略获得LU节点的初始值，提取子图Gs中LU节点的位置xk，作为初始值。设k=0，表示第k次迭代；

(2) 计算搜索方向qk：qk=-∇fs(xk)；

(3) 计算步长：如果k=0，则通过回溯直线搜索法确定步长α0；否则通过式(27)计算步长αk；

(4) 更新子图Gs中LU节点位置：xk+1=xk+αkqk；

2.3 子图融合

在构建图模型时，将WSN构成的无向图G以LU节点为中心分解为n个部分重叠的子图。如图1所示，同一个LU节点会位于不同的子图中。因此，对每个子图优化求解后，对于相同的LU节点会有不同的估计值。需要对子图进行融合，从而得到每LU节点的估计值。而且可能会出现某个子图由于可用的信息较少，导致估计出的LU节点位置误差较大的问题。子图融合可以有效地降低这部分节点的误差，从而提高整体WSN的定位精度。子图融合公式如下：

(28)

经过上述分析，分布式定位算法的整体流程如算法1所示。

算法1分布式定位算法。

准备工作：将N个传感器随机部署在检测区域内，其中有m个LA节点，n个LU节点，通信半径为R。以LU节点为中心，通信半径内与LU节点直接相连的节点为邻居节点，构成一个子图。从而将WSN划分为n个部分重叠的子图。令t=0。

输入：使用节2.2.1中采用的极大似然估计法及相关规则，对LU节点进行粗略的初始定位，定位结果为p(t)。将其作为步骤(1)中进行优化求解的初始值；

(1) 采用节2.2.2的Barzilai-Borwein梯度法对划分好的子图进行优化求解；

(2) 采用节2.3提出的子图融合的方法，对部分重叠的子图进行融合，得到第t+1次迭代的定位结果p(t+1)；

输出：p(t+1)作为最终定位结果。

2.4 计算复杂度分析

3 仿真结果及分析

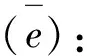
(29)

表1 实验参数的设置与说明

实验3为了研究文中算法在不同网络规模和噪声情况下的定位效果，本次实验节点分布区域为[-0.5，0.5]2，改变节点总数N、通信半径R、LA位置噪声因子τ2进行仿真，并与文献[5，7-8]进行对比。仿真参数设置和定位结果如表2所示。可以看出，在相同规模的无线传感器网络中，对LA位置添加噪声后，各算法的定位精度均会下降。在小规模无线传感器网络(N<500)中，文中算法与文献[5]提出的集中式定位算法相比，有近似的定位精度，但在大规模无线传感器网络(N≥500)中，集中式定位算法便无法定位，而文中算法仍有较好的定位精度，而且与文献[7-8]提出的分布式定位算法相比，在相同的仿真参数下，始终有更好的定位精度。综上所述，笔者提出的分布式定位算法有良好的扩展性，可有效用于大规模的无线传感器网络中，并且有较高的定位精度。

图2 不同锚节点数目下的平均定位误差

表2 文中算法与文献[5，7-8]算法在不同参数下实验结果对比

4 结束语

针对无线传感器网络定位精度较低、扩展性不高问题，笔者提出了一种分布式定位算法。首先将整个无线传感器网络构成的无向图分解为部分重叠的子图，并构造出子图的优化问题，然后采用笔者所提算法进行优化求解。求解的过程包括子图内的位置估计和部分重叠子图的融合。仿真实验证明，与现有集中式定位算法相比，有较高的扩展性，可有效用于大规模无线传感器网络。与现有分布式定位算法相比，有更高的定位精度。可见笔者提出的算法具备一定的优势，可以为无线传感器网络的经济、高效、实用性发展提供可靠的技术支持，进而促进无线传感器网络在环境科学、医疗健康等多个领域的应用。