农村三产融合背景下基于ARIMA 模型对陕西省农村就业人数的分析与预测

□杨 艳，雷咪咪

（1.陕西学前师范学院数学与统计学院，陕西 西安 710100；2.西安财经大学统计学院，陕西 西安 710100）

1 研究背景

农村一二三产业融合发展，是社会经济发展到一定阶段的必经之路。《中共中央关于制定国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建议》提出优先发展农业农村，全面推进乡村振兴，推动农村一二三产业融合发展。2021 年底中央农村工作会议强调要聚焦产业促进乡村发展，深入推进农村一二三产业融合，大力发展县域富民产业，推进农业农村绿色发展，让农民更多分享产业增值收益。

陕西是华夏农耕文化的重要发祥地之一，农耕文化历史悠久，农业资源丰富多样，农业科技力量雄厚，特色产业优势突出，农村经济发展平稳。根据《陕西省统计年鉴2021》的数据可知，2020 年底陕西省总人口3 955 万人，其中城镇人口2 478 万人，占总人口的62.66%；乡村人口1 477 万人，占37.34%。陕西省经济发展势必会改变就业形势，各产业的就业规模、就业结构及就业质量都会发生变化。从陕西省农村实际情况看，一二三产业融合尚存在资金、技术、人才等一系列问题。随着工业化、城镇化迅速发展，农村劳动力“空心化”、老龄化、人才支撑不足等问题加剧。农业就业岗位少，农民收入增长缓慢，很多农村青壮年劳动力离开农村，严重影响了三产融合经济效应的充分发挥。三产融合在推动经济增长的同时，也产生了就业创造和就业消失效应。因此，研究农村一二三产业融合的就业效应，对“十四五”期间补齐陕西省农村发展短板、全面推进乡村振兴具有积极意义。其中，陕西省农村劳动力市场发展、农村劳动力资源优化配置与当前农村一二三产业融合进程息息相关。

本研究利用ARIMA 模型对1998—2017 年陕西省农村就业人口序列进行分析和建模，进一步研究三产融合背景下陕西省农村的就业效应，为当地经济发展提供参考。

2 ARIMA 模型

2.1 ARIMA 模型概述

ARIMA 模型是将非平稳时间序列通过差分运算转化为平稳时间序列，然后利用平稳时间序列的建模方法，对经过差分后的平稳序列拟合ARMA 模型。利用这种建模思路所拟合的模型称为求和自回归移动平均模型，记为ARIMA 模型。

ARIMA 模型结构：若序列{x}可以通过阶差分转化为平稳时间序列，即{x}={△x}是一个平稳时间序列，且可以拟合一个平稳可逆ARMA（，）模型，则序列{x}可以拟合如下形式的模型。

式中：Φ()=1--…φB，Θ()=1--…θB。

具有上述结构的模型称为求和自回归移动平均模型，记为ARIMA（，，）。移动平均自回归模型（ARIMA）是一类常用的时间序列模型，精度较高，适合短期预测，可以用来分析时间序列的随机性、平稳性等特征，从而选择适当模型进行预测。

2.2 ARIMA 模型建模步骤

获得观察值序列，检验时间序列是否是平稳的时间序列。如果是平稳的，进一步检验该序列是否是白噪声，如果不是白噪声序列，则可以拟合ARMA 模型。建模过程如图1 所示。

图1 ARIMA 模型建模流程图

3 基于ARIMA 模型对陕西农村就业人数的分析与预测

3.1 数据来源

根据国家统计局网站上提供的数据，从1978 年起开始有农村就业人数的记录。从《陕西省统计年鉴2021》中收集整理了1978—2020 年陕西省乡村就业人数的时间序列，见表1。

由表1 的数据可知，从1978 年起，陕西省农村就业人数迅速增长，1994 年起增速减缓，2000 年开始小幅回落，2003 年起又开始稳步增长，从2006 年开始再次回落，2009 年起基本保持逐年递减的趋势。

由于统计指标的调整，陕西省农村就业人数从1999 年开始有了具体的产业分类统计数据。根据研究需要，本研究从表1 中截取了1998—2017 年的时间序列进行数据分析与预测。

表1 1978—2020 年陕西省乡村就业人数

3.2 ARIMA 模型分析

3.2.1 数据的处理与分析

平稳性检验是构建ARIMA 模型的首要步骤。首先对陕西乡村就业人数的时间序列进行平稳性检验。利用adf.test 函数进行ADF 检验，经ADF 检验发现，Dickey-Fuller=0.741 411，值为0.99，在5%置信水平下拒绝原假设，说明此序列是非平稳序列。结合图2陕西省乡村就业情况的时序图可知，数据前期呈上升趋势，随后呈现持续下降趋势，因此需要对数据进行平稳化处理。使用R 语言，运行的ADF 检验结果如下。

图2 陕西省乡村就业情况时序图（1998—2017 年）

3.2.2 平稳化处理

对一阶差分后的新序列进行平稳性检验，经ADF检验后，发现=0.019 34，通过了稳定性检验，结合图3 陕西省乡村就业人数一阶差分时序图可知，一阶差分后的序列是平稳序列，不存在单根问题，因此ARIMA（，，）模型中的参数=1。使用R 语言，运行的ADF 检验结果如下。

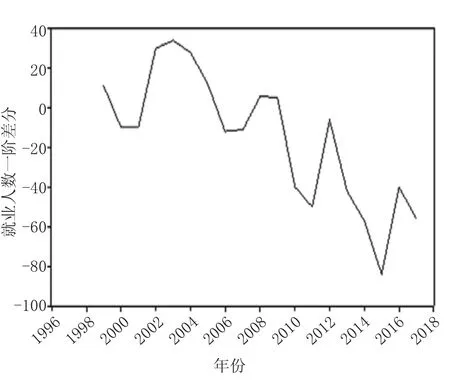
图3 陕西省乡村就业人数一阶差分时序图（1998—2017 年）

3.2.3 序列白噪声检验

白噪声检验的原理：如果延迟6 阶和延迟12 阶的LB 统计量的值均小于0.05，则可以判断此序列是一个非白噪声序列。经过检验，由差分获得的平稳序列为平稳非白噪声序列。使用R 语言进行白噪声检验的结果如下。

3.2.4 模型识别

对平稳非白噪声序列进行建模。根据自相关图和偏自相关图来选择模型，对一阶差分后的序列进行自相关（acf）和偏自相关（pacf）分析，并绘制出自相关系数（ACF）和偏自相关系数（PACF）图，见图4。

根据图4 可知，滞后阶数逐渐增加时，自相关系数（ACF）逐渐减小趋近于0；偏自相关图在1 阶后减小到0，故选择ARIMA（1，1，0）模型。在R 语言环境下，使用ARIMA 函数的具体建模过程如下。

图4 自相关系数（ACF）和偏自相关系数（PACF）图

3.2.5 模型检验

合理的模型其残差应该满足均值为0 的正态分布。绘制正态Q-Q图并进行模型残差自相关系数分析。

构建的模型残差理论分位数和样本分位数绝大多数落在线上，见图5，说明残差近似均数为0 的正态分布。

图5 正态Q-Q 图

进一步进行残差白噪声检验（Ljung-Box 检验），残差为纯随机序列即白噪声，Ljung-Box 检验发现所有值＞0.05，拒绝原假设，即可认为残差的自相关系数为0，模型ARIMA（1，1，0）可以比较好地拟合本数据。在R 语言环境下，对模型ARIMA（1，1，0）的残差序列进行白噪声检验，结果如下。

3.2.6 模型拟合和模型预测

利用SPSS 软件拟合陕西省乡村就业人数真实值和ARIMA 模型拟合值的趋势，发现ARIMA（1，1，0）模型的趋势与真实值趋势差别不大，大多数真实值都落在拟合值95%的置信区间中，较好地拟合了陕西省乡村就业人数，见图6。

图6 模型拟合图

利用ARIMA（1，1，0）模型预测2018—2020 年陕西省乡村就业人数，显示乡村就业人数都在ARIMA模型预测值95%置信区间内，预测结果见表2。实际值与预测值的平均相对误差为5.817 7%，表示这个模型能较好地预测趋势效果，可以较好地把握陕西省乡村就业人数的趋势。

表2 ARIMA（1，1，0）模型乡村就业人数预测值

4 结论

对1998—2017 年陕西省乡村就业人数时间序列进行分析并建立模型。因为1998—2017 年陕西省乡村就业人数的时间序列非平稳，故而使用Box-Jenkins法建立ARIMA 模型。根据所建立的ARIMA（1，1，0）模型，对陕西省农村就业人数进行预测，达到了较好的短期预测效果。通过对陕西省农村就业人数的时间序列进行分析，可以从就业规模的角度反映陕西省农村一二三产业融合的就业效应，为进一步研究提供方法和思路，也有助于在地方制定经济发展目标时提供决策依据。