可变径刮管器结构设计及测试

王晓，李清涛，刘传刚，刘景超，邢洪宪，王尧，邓晗，姚智翔

中海油能源发展股份有限公司 工程技术分公司（天津 300452）

0 引言

刮管器是重要的套管内壁清洁工具，其性能的好坏在完井作业中对工作液清洁、管柱下入摩阻、封隔器密封、钢丝作业、储层保护等有重要影响。目前常用的刮管器多为单一工作内径的刮管器，仅能在一种内径的井筒中进行刮管清洗作业[1-4]。当需要清洗的井段为两种不同内径时，则需要更换不同的刮管器。由于海上油田刮洗的位置通常在2 000~3 000 m深度，更换刮管器需要耗费大量的时间，严重影响了海上作业效率。

设计了一种可变径刮管器，适用于159.4~220.5 mm（7"~95/8"）套管的刮管需求，并对其核心结构板簧进行了优化设计。基于理论分析和有限元数值模拟方法，研究了滑套可变径刮管器板簧结构的力学性能，并通过功能实验与理论、数值模拟结果进行对比，验证了理论研究的准确性。相关研究方法和结论可为新型可变径刮管器的设计提供参考。

1 系统构成与结构设计

1.1 工作工况

海上油田套管根据设计差异，不同位置通常有不同的尺寸。其中一种较为常见的结构为上部220.5 mm（95/8"）套管，下部159.4 mm（7"）套管，如图1所示。当进行刮管清洗作业时，需要先下220.5 mm的刮管器，刮洗完成后，起出刮管器，更换159.4 mm的刮管器，再次下入井中，进行刮洗作业。由于刮洗的位置普遍较深，通常在2 000~3 000 m深，更换刮管器需要耗费大量的时间。

图1 海上常见套管结构示意图

可变径刮管器在220.5 mm和159.4 mm套管内都可以作业，即可以刮完220.5 mm的套管后，直接刮洗159.4 mm套管，一次完成220.5 mm和159.4 mm套管的刮洗作业，如图2（a）、（b）所示。根据相关使用要求在220.5 mm和159.4 mm套管内时，板簧的弹力需要控制在300~1 300 N。

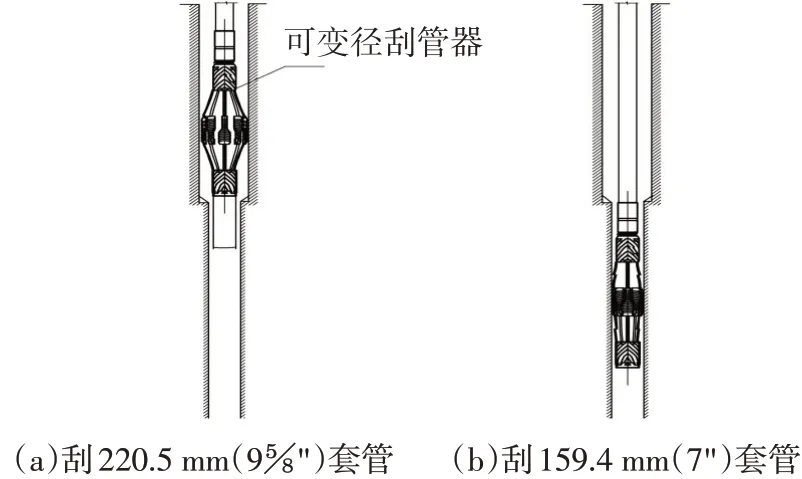
图2 可变径刮管器刮套管示意图

1.2 可变径刮管器基本结构

可变径刮管器的主要结构如图3所示，主要由芯轴、上接头、弹簧、固定栓、板簧、刮刀组成。板簧的两端安装在固定套上，对板簧起到固定和约束作用，刮刀片安装在板簧的中央。其中，板簧是可变径刮管器的核心部件，其主要作用是通过板簧压缩后产生的反力作用在卡瓦，使卡瓦贴紧套管壁，板簧反力的大小直接决定了刮管器刮削力的大小。板簧结构的设计是影响刮管器设计的核心因素，需要根据使用工况对板簧结构进行详细的分析及优化设计。

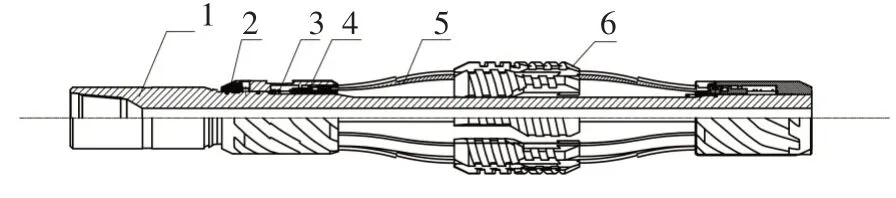
图3 可变径刮管器主要部件构成示意图

2 可变径刮管器板簧结构受力理论分析及优化设计

2.1 板簧结构受力分析

板簧结构是一种常见的弹性结构，普遍应用于汽车、建筑等领域，具有力学性能稳定、强度高等优点[5-8]。为了满足大变径的需求，设计采用了弓形的结构，如图4（a）所示。可变径刮管器主要通过径向位移载荷作用下的弹性变形来实现刮削和变形功能，其板簧结构可简化为一端固定，一端简支的梁结构进行受力分析。压力载荷施加于板簧结构中间位置，板簧结构及截面形状如图4（b）所示。

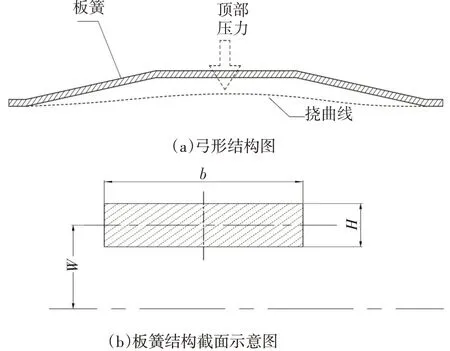
图4 变径刮管器板簧结构示意图

板簧截面惯性矩I为：

根据简支梁挠度与载荷力公式：

式（1）、式（2）联合可得，板簧在工作状态中受到的顶部压力P为：

同时,对于刮管器存在：

所以：

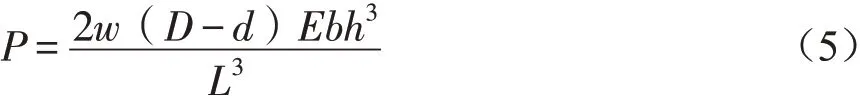
式中：b为板簧宽度，mm；h为板簧高度，mm；P为板簧的顶部压力，N；L为板簧长度，mm；E为板簧材料弹性模量，MPa；w为板簧径向方向的压缩距离，mm；D为刮管器的外径，mm；d为对应套管的内径，mm。

刮管器工作工程中刮削力F为：

式中：F为所有板簧刮削过程的轴向力，N；n为板簧的数目；μ为刮板与套管间的摩擦系数。

2.2 板簧结构优化设计

板簧结构所用材料为60Si2Mn，弹性模量为2.06×1 011 Pa，泊松比为0.3，板簧长度1 000 mm，其截面宽度为22 mm，厚度为5 mm，板簧的压缩高度需要设计计算，而板簧的高度通过刮管器的外径进行控制。根据上述公式计算求得刮管器外径对板簧支反力的影响关系，如图5所示。

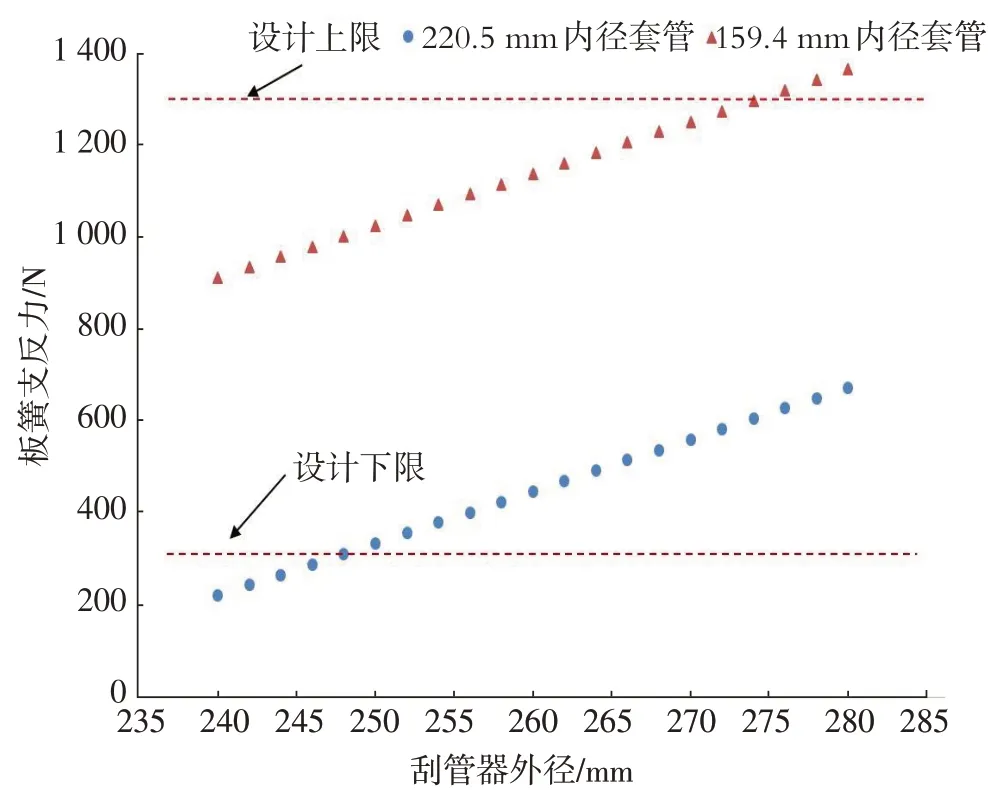
图5 变径刮管器板簧支反力随外径变化曲线

根据设计要求，刮管器的板簧在220.5 mm和159.4 mm套管内，板簧的弹力需要控制在300~1 300 N。由图5可知，在220.5 mm和159.4 mm套管内刮管器板簧的支反力均随着外径的增大线性增大。当外径大于247 mm时，板簧支反力大于300 N；当外径小于274 mm时，板簧支反力小于1 300 N。因此刮管器的外径D应满足247 mm≤D≤274 mm。考虑到支反力过大容易造成板簧变形，取刮管的外径为260 mm。

3 可变径刮管器板簧有限元分析

3.1 可变径刮管器板簧模型建立

为了更加准确了解板簧的支反力及变形情况，检验其强度是否满足要求，目前主要通过有限元法建立其模型，模拟计算在工作状态下板簧的变形情况及应力分布[9-10]。

主要步骤如下：①根据确定的板簧基本结构及尺寸建立板簧的三维模型，并在板簧的顶部设置一个矩形压块，模拟套管对板簧的压缩作用，板簧和压块之间设置接触对。②在板簧的两端施加滑动约束，压块上施加向下的位移荷载，模拟计算不同外径的套管对刮管器板簧的压缩作用。对所有结构划分网格，划分网格后的模型如图6所示。在压缩过程中，板簧的变形较大，计算采用大变形的非线性求解器。

图6 板簧的网格模型和接触设置

3.2 数值模拟计算结果分析

运行求解得到板簧在5、20、35、50 mm压缩距离下表面的Mises应力分布和变形情况，计算结果汇总应力云图如图7所示。

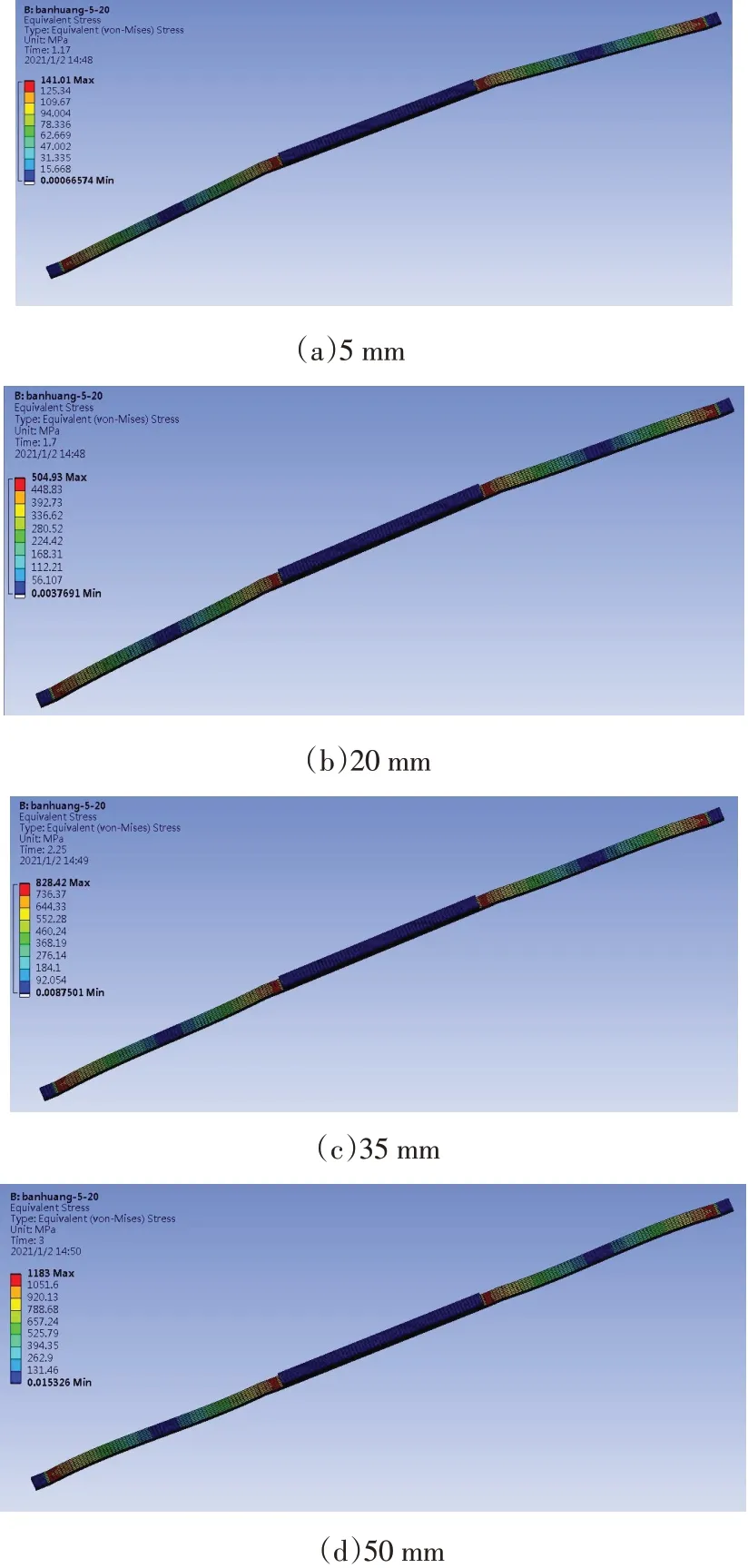
图7 不同压缩距离时板簧表面Mises应力云图

当压缩距离为5、20、35、50 mm时，板簧表面最大Mises应力主要发生板簧的根部，其最大值分别为141、504、828、1 183 MPa。板簧的材质为合金弹簧钢60Si2Mn，屈服强度1 274 MPa，表面各处的应力均小于其屈服强度，不会发生屈服变形，说明板簧的强度满足要求。

3.3 结果对比分析

对数值模拟结果进行后处理，得到不同压缩距离时板簧的支反力和表面最大Mises应力,并计算板簧在不同压缩距离下支反力的理论值，汇总对比如图8所示。

图8（a）为不同压缩距离时板簧的理论与数值模拟支反力对比图，两者的变化规律完全一致，计算结果非常接近，数值模拟计算结果略大于理论计算。以压缩距离为50 mm时为例，支反力的理论计算值与数值模拟值分别为1 133 N和1 210 N，误差仅6%。

图8（b）为不同压缩距离时板簧的最大表面应力随压缩距离的变化情况，其分布几乎成线性规律。在设计的压缩行程内，板簧的表面Mises应力始终小于板簧的屈服强度，不会发生屈服变形，满足设计要求。

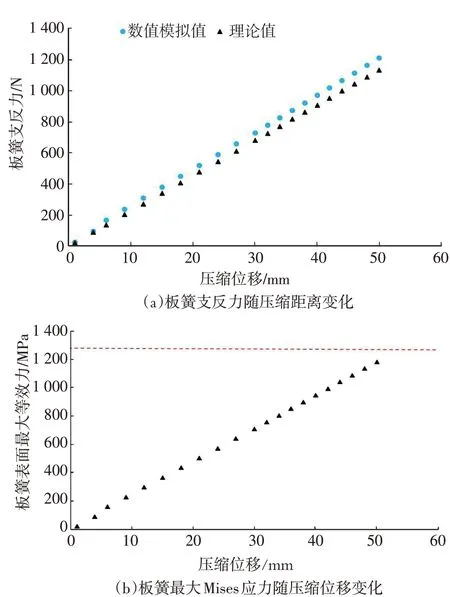
图8 不同压缩距离时板簧支反力和最大Mises应力变化

4 实验测试及现场应用

4.1 实验测试

为了进一步验证设计的准确性和可靠性，需要对加工好的刮管器板簧结构进行试验测试。测试过程如图9所示，将板簧及固定套安装在一根轴上，轴的尺寸与刮管器芯轴的尺寸保持一致。测试使用的为TWL型拉压试验机，加载方式为位移控制加载，加载速度为50 mm/min。压力试验机的压头作用在板簧的中部，通过电脑记录板簧的压缩位移和支反力变化。

测试得到板簧的压缩位移和支反力变化如图9（b）所示，在压缩过程中板簧的支反力随压缩位移线性增加，与理论及有限元分析一致。当压缩位移为50 mm时，实验测得的支反力为1 250 N，其数值模拟计算为1 210 N，理论计算结果为1 133 N。与实验测试结果相比，理论计算结果与数值模拟计算结果分别比实验测试结果小9.36%和3.20%。可见数值模拟计算的准确性略高于理论计算结果，并进一步验证了设计计算的合理性。

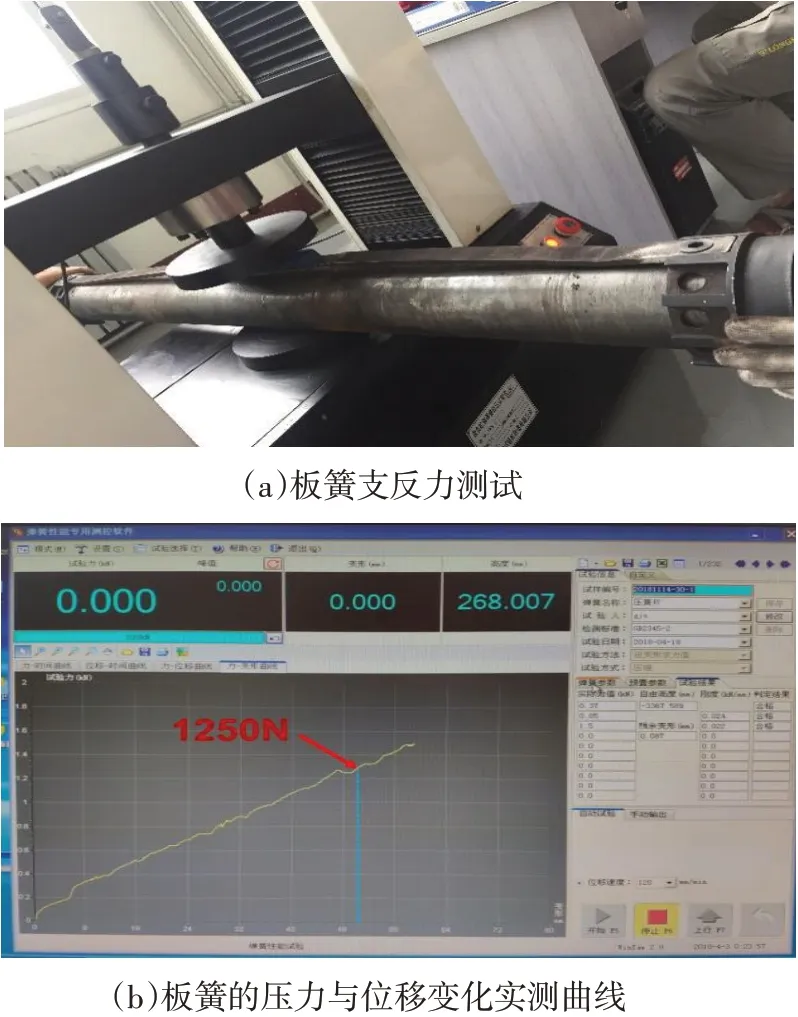
图9 板簧的实验室测试

4.2 现场应用

可变径刮管器取得实验测试成果后，开始在海上油田常规套管井和防腐套管井应用。目前已经成功应用于渤海、南海等多个海域，使用超过数十口井次。工具出井后没有出现变形、断裂等情况，并取得了良好的刮管效果。

5 结论

1）设计了可用于159.4~220.5 mm（7"~9⅝"）套管的可变径刮管器，对设计的可变径刮管器板簧结构进行了理论分析，得到了板簧支反力和长度、宽度、压缩高度等结构参数的规律，并初步优化了结构尺寸。

2）对可变径刮管器板簧结构建立了三维有限元模型，分析发现板簧表面最大Mises应力随压缩距离线性增大，且达到最大设计压缩距离50 mm时，最大Mises应力为1 183 MPa，小于其屈服强度，满足设计要求。

3）对可变径刮管器板簧结构进行了实验测试和对比分析，发现当压缩位移为50 mm时，实验测得的支反力为1 250 N、数值模拟结果为1 210 N，理论分析计算结果1 133 N，理论计算结果与数值模拟结果与实验测试结果分别相差9.36%和3.20%。验证了计算分析的合理性。

通过多次现场应用验证了设计的合理性，能够显著提高现场刮管洗井的工作效率，也为其他尺寸可变径刮管器的设计提供参考。