常压低温环境下抛物面薄壁结构热平衡特性分析
2022-05-27张良俊张婉雨陈燕地杜懿岑吴静怡
杨 光,张良俊,张婉雨,陈燕地,杜懿岑,吴静怡
(1.上海交通大学 制冷与低温工程研究所,上海 200240;2.上海市空间飞行器机构重点实验室,上海 201108)
0 引言
航天器在轨运行期间,由于周期性地经过日照区和阴影区,外部热流和温度会发生剧烈的变化[1-3]。航天器中广泛采用的太阳能帆板、天线等结构件,将不可避免地在较大的温度梯度作用下产生热应力,发生屈曲、变形甚至振动。天线等结构件是航天器载荷的重要组成部分[4],其表面的非均匀温度分布会造成天线型面精度不同程度的变差,可以认为,天线等结构件的热变形对航天器在轨运行的安全性和可靠性有着重要的影响[5-7]。此外,随着航天器电子通信性能和精度要求的不断提高,对天线的型面精度、张力均匀性的要求也越来越高[8]。
国内外学者针对空间天线的热-结构特性做了大量研究。刘国青等[9]对航天器高稳定结构热变形进行仿真分析,并采用非接触式测试方法进行验证,结果显示,在轨结构热变形为2~30 μm。麻慧涛等[10]针对抛物面天线开展外热流、温度场、热变形和热应力场等机热一体化集成分析,得出了对空间结构设计有指导意义的结论。张惠峰等[11]采用热辐射-热传导理论,对天线不同在轨位置下的温度情况进行仿真计算,发现阴影区的温度梯度较大,对抛物面天线不利。Dicarlo等[12]通过简化模型,实现了对昼夜温差与天线表面温度间关系的预测。Guo等[13]分析了天线在轨时的热流变化规律,计算了天线受热流变化影响产生的热变形,研究了热环境下天线电信号的失真情况。以上研究凸显了航天机构热变形研究的重要性。
在地面上利用空间环境模拟试验系统开展相关试验是进行热变形研究与预测的重要手段。以低温氮气/氦气为工质的常压热环境试验系统具有传热效率高、成本低等优势,近年来得到了广泛的应用和发展[14]。但在地面试验环境中航天器的传热机制与空间状态无法完全一致。为了明确地面环境带来的影响,并将试验数据进行等效性修正以反映实际空间在轨状态,必须对常压低温环境下航天器的热平衡以及温度分布特性进行研究。本文以刚性薄壁抛物面天线结构为对象,定量分析其在地面常压热环境模拟试验空间中的耦合传热特性。以明确在不同的外热流、等效导热系数以及辐射系数条件下,抛物面表面温度分布、体平均温度和温度标准差等温度特性,在此基础上,获得对流、导热、辐射传热的热流平衡以及抛物面压力特性等关键数据。
1 模型与方法
1.1 物理模型
航天器常压热环境模拟试验系统的高/低温循环流程如图1所示。计算区域为试验舱体及其内部的抛物面薄壁天线,如图2所示。抛物面形状方程为x2+y2=2z。端面圆周直径为R1,壁面厚度为Δ1。

图1 航天器常压热环境模拟试验系统示意图Fig.1 Schematics of a typical thermal environment test system for spacecraft

图2 试验舱体及其内部的抛物面天线结构物理模型图Fig.2 Schematic diagram of physical model used in simulation
由液氮气化产生的低温氮气从舱体顶部入口均匀流入,从底部出口流出,形成均匀稳定的低温环境;舱体内壁面假设为恒温,Tw=180 K,与试验舱体内的低温送风相结合,形成对流-辐射耦合传热。为了模拟外部热流对抛物面结构传热的影响,在其下表面施加均匀的热流进行加热。抛物面辐射系数εk、下表面施加的热流密度Q、固体的等效导热系数λ为影响抛物面结构传热的关键物理量。系统内结构件的尺寸如表1所列。
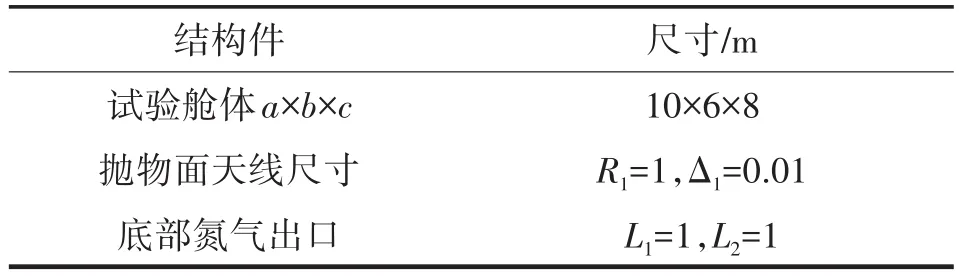
表1 系统内结构件尺寸表Tab.1 Dimensions of key structures in the system
1.2 数学模型和计算方法
以典型的低温保温工况为例进行分析,当试验舱体的氮气入口温度T0=150 K,入口雷诺数Re为9 500时,气体流动状态属于三维空间内的湍流对流传热问题。雷诺数表示如下:

式中:x、y、z为笛卡尔系统坐标轴,m;u、v、w为各方向的速度,m·s-1;U为矢量速度,U=(u,v,w);p为压力,Pa;t为时间,s;T为温度,K;c为比热容,J·kg-1·K-1;λ为导热系数,W·m-1·K-1;qr为内热源的发热量,W/m2;S1和S2为方程求解中设置的源项。
计算过程中,模型采用Lam-Bremhorst低雷诺数k-ε湍流模型。试验舱体壁面处采用无滑移速度边界条件。将抛物面天线结构的导热系数简化为各向同性。由于氮气辐射能力极弱,因此仅考虑壁面与抛物面天线间的固体间辐射传热,假设壁面为理想灰体,即辐射系数等于吸收系数。计算过程中考虑氮气的物性参数随温度变化,数据来自REFPROP数据库。将固体壁面分为N个离散的单元,并计算各单元间的辐射传热,过程如下:
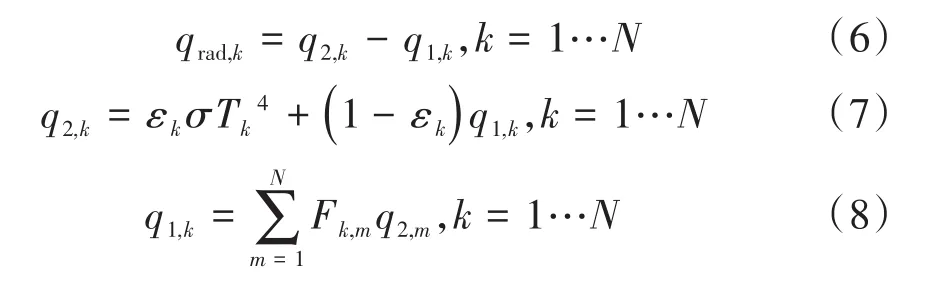
式中:εk为辐射系数;k是单元编号;下标1为输入;下标2为输出;q2,k为第k个单元的输出热量,W/m2;q1,k为第k个单元的输入热量W/m2;两者的差是第k个单元的净辐射量,qrad,k;Fk,m是第m和第k个单元间的角系数(无量纲)。
为了定量分析不同边界条件下抛物面薄壁结构的热平衡特性,给出几个温度参数定义。

式中:S为表面积,m2;V为体积,m3;下标i为单元编号;下标j为表面编号;Tavg,j为第j个表面的平均温度;Tj,i为第j个表面上的第i个单元的温度,K;Ti为空间内第i个单元的温度,K;Tavg为固体体积平均温度,K。表面和体积平均温度用于反映抛物面结构的热平衡特性;温度标准差σ用于反映抛物面结构的温度分布均匀程度,该数值能体现出对热变形的影响。
1.3 网格无关性检验与模型准确性验证
为了保证在计算准确度的同时控制计算成本,进行网格数量的无关性验证。因研究内容主要为抛物面天线温度及其相关特性,在相同的边界条件下,选择抛物面天线的体平均温度作为指标进行验证,结果如图3(a)所示。当网格数高于200万以上时,不同网格下的温度计算结果基本一致,相对误差小于1%,因此选择网格数目为270万的非结构化网格进行计算,且近壁面第一层网格节点相对厚度(Y+)小于5,网格偏斜率小于0.6。
仿真分析之前,利用实际试验数据对计算模型的准确性进行了验证,具体试验流程已在前期工作中进行了介绍[15-16]。图3(b)为在送风流量8 000 m3·h-1,送风温度195 K时,由试验舱体内15个温度测点所获得的温度标准差随时间的动态变化。可以看出,在约900 s的降温时间内,仿真结果与试验数据的趋势一致,平均相对误差在10%以内,证明了上述 计算模型具有较高的准确性。

图3 网格数量无关性与模型准确性验证Fig.3 Grid independence and model accuracy verifications
2 结果与讨论
2.1 壁面辐射传热的影响及抛物面表面的传热平衡
当无外热流时,在不同的抛物面表面辐射系数条件下,上下表面以及体平均温度的变化如图4所示。随着辐射系数从0提高到1,表面及体平均温度呈单调性上升,但不显著,仅提升约0.7 K。抛物面温度分布均匀,且下表面的温度始终略高于上表面。

图4 不同辐射系数下抛物面温度变化Fig.4 Variation of average temperature of the parabolic antenna under different radiation coefficients
图5为抛物面上下表面由不同传热途径产生的传热量变化。在无外热流加入的条件下,抛物面的上表面温度始终低于壁面温度,因此净辐射传热始终为从壁面传至抛物面表面,因此辐射传热量为负值。抛物面上表面受下沉气流冷却,因此该表面的对流传热量为正值。随着辐射系数增大,上表面温度上升,与周围流体温差增大,对流传热量也增大。而对于下表面,当辐射系数为0时,抛物面传热平衡体现为:下表面附近流体以对流方式吸热,热量通过热传导传递至上表面,再经对流传至上表面流体。当辐射系数逐渐增大时,下表面温度逐渐升高,直至升高到εk≥0.4时,下表面温度高于周围流体温度,其对流换热量为正值,即通过下表面向周围流体传热,传热量随辐射系数的增加而增大。

图5 不同辐射系数下抛物面上下表面热流平衡Fig.5 Heat flow equilibrium on the upper and lower surfaces of parabolic antenna
图6为抛物面上下表面温度标准差随辐射系数的变化情况。在无外热流条件下,上下表面温度标准差基本一致,均低于0.04 K。随着辐射系数增大,温度标准差呈现先减小再增加的趋势,并在εk=0.2时降低至极小值。其原因是在εk=0.2时,辐射传热导致抛物面的表面温度更接近周围温度,从而分布更均匀;而辐射系数继续增大时,表面温度升高,与周围环境流体间的温差增大,表面温度均匀性逐渐变差。
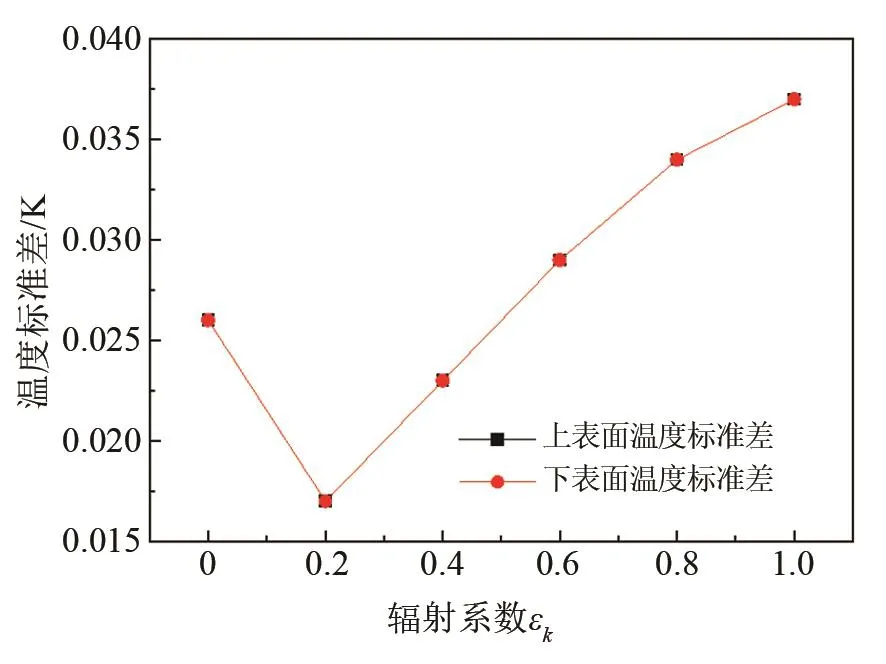
图6 不同辐射系数下抛物面上下表面温度标准差Fig.6 Standard deviation of temperature for the upper and lower surface of the parabolic antenna under different radiation coefficients
2.2 抛物面表面施加热流对温度分布的影响
当对抛物面下表面施加密度为0 W·m-2、250 W·m-2、500 W·m-2和 1 000 W·m-2的外热流时,试验舱体中心截面上的温度分布如图7所示。随着加热功率增大,气体空间的等温线分布规律几乎不变,表明加热抛物面对试验空间整体热流的流动形态与温度分布特征的影响较小。

图7 不同外热流密度下试验舱体中心截面上的温度分布Fig.7 Temperature distribution at the central plain under different external heat fluxes
图8为在抛物面天线下表面施加密度为0 W·m-2、250 W·m-2、500 W·m-2和1 000 W·m-2的外热流时抛物面天线的温度分布。在没有外热流条件下,抛物面上最高温度位于其几何中心的凹面处,最低温度位于远离中心的位置。随着外热流密度增大,抛物面表面温度逐渐升高,温度梯度增大,温度沿中心轴呈中心对称分布,靠近圆周区域的径向温度梯度大于靠近圆心区域处的温度梯度。

图8 不同外热流密度下抛物面天线的温度分布Fig.8 Temperature distributions of parabolic antenna under different external heat flux
图9为在抛物面天线底面施加不同密度的外热流时,抛物面天线的平均温度变化曲线。可以看出,抛物面上下表面及体平均温度随着热流密度增加呈近似线性升高,斜率约为0.02 K·m-2·W-1。此外,上下表面温度几乎保持一致,在1 500 W·m-2热流密度时温度偏差为0.5 K。

图9 不同外热流密度下抛物面天线的平均温度变化Fig.9 Variation of average temperature of the parabolic antenna under different external heat fluxes
图10为不同外热流密度下抛物面上下表面热流平衡情况。从图中可以看出,随着外热流增大,辐射传热所占比例逐渐小于对流传热,这是由于参与辐射的抛物面与试验空间侧壁面的温差较小,而与周围流体的温差较大。尽管外热流施加至抛物面的下表面,但抛物面上表面的对流换热量始终大于下表面,其原因有两个方面:第一,低温氮气是自上而下冷却试验空间及抛物面的;第二,上表面周围被加热的流体更容易受浮升力作用形成自然对流或混合对流场,而下表面受热的流体仅能沿着表面流向四周,不利于对流传热。
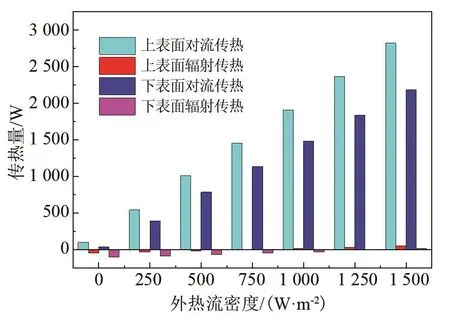
图10 不同外热流密度下抛物面上下表面热流平衡情况Fig.10 Heat flow equilibrium on the upper and lower surfaces of parabolic antenna under different external heat fluxes
图11为不同外热流密度下抛物面上下表面的温度标准差变化。随着施加的外热流从0 W·m-2增加到1 500 W·m-2,上下表面的温度标准差呈线性增大,由0.1 K升至约1.5 K。下表面温度标准差始终小于上表面。表明施加热流会导致抛物面表面对流换热强度增大,进而导致其温度均匀性变差。

图11 不同外热流密度下抛物面上下表面温度标准差变化Fig.11 Standard deviation of upper and lower surface temperature of parabolic antenna under different external heat fluxes
图12为不同外热流密度下抛物面所受到的气体净压力变化。在浮升力的作用下,顶部低温氮气下沉,在抛物面天线四周形成绕流,气流对抛物面总体压力朝下,在无外热流作用下约为14 N。施加外热流后,抛物面温度升高,其表面处的流体受热上浮,对抛物面起到向上提升的作用。因此向下的合力随热流密度的增大而减小,在外热流为1 500W·m-2时降至11.6 N。

图12 不同外热流密度下抛物面所受净压力变化Fig.12 Vatiation of pressure on the paraboloid under different external heat fluxes
2.3 抛物面等效导热系数对温度及传热的影响
针对具有不同等效导热系数的抛物面结构,当下表面施加外热流1 000 W·m-2时,抛物面的温度分布如图13所示。导热系数较小时,热量传递需要更大的温差,因此抛物面整体的温度梯度大。温度分布特征体现为靠近中心区域的径向温度梯度较小,而靠近圆周区域有较大的温度梯度。相反,当等效导热系数较大时,整体温度梯度小,径向温度梯度更均匀。

图13 不同等效导热系数下抛物面天线的温度分布Fig.13 Temperature distributions of parabolic antenna under different equivalent thermal conductivities
图14为对下表面施加外热流1000 W·m-2时,不同等效导热系数下抛物面天线的平均温度变化趋势。可以看到,当等效导热系数为2 W·m-1·K-1时,上下表面间的温度差为10 K。随着等效导热系数增加,上下表面的平均温度逐渐趋于同一值。此外,抛物面结构的体平均温度也随等效导热系数的增加呈单调减小的趋势。
图15为下表面施加外热流1000 W·m-2时,不同等效导热系数下抛物面天线的温度标准差变化。当等效导热系数为2 W·m-1·K-1时,抛物面上下表面的温度标准差分别为3.6 K和2.8 K。随着等效导热系数增大,温度标准差显著下降,在200 W·m-1·K-1时降至约1 K,表明增大抛物面天线的等效导热系数有助于提高表面温度分布的均匀性。
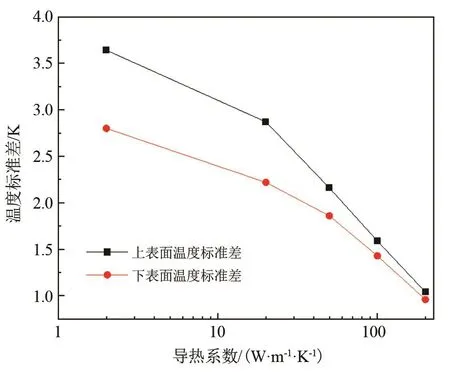
图15 不同等效导热系数下抛物面天线的温度标准差变化Fig.15 Standard deviation of temperature of the parabolic antenna under different thermal conductivities
3 结论
本文针对常压热环境试验系统低温试验舱体内的刚性薄壁抛物面天线结构,通过数值模拟与试验验证定量研究其在低温耦合传热条件下的热平衡与温度分布特性。主要结论如下:
(1)辐射传热对抛物面天线热平衡影响较小,当辐射系数在0~1间变化时,抛物面天线的体平均温度仅上升0.5%,上下表面温度标准差变化0.02 K。但辐射传热会影响整体的热平衡特性,当εk<0.4时,下表面通过对流传热从周围流体吸热;而当εk≥0.4时,下表面通过对流传热向周围流体放热。
(2)加热抛物面表面对试验空间整体热流流动形态与温度分布特征的影响不显著,但对抛物面本身的温度分布有着决定性影响。随着外热流密度增大,抛物面表面温度呈线性升高,温度标准差增大,温度分布沿中心轴旋转对称。外热流增加至1 500 W·m-2时,上下表面温度标准差变化约1.5 K。
(3)等效导热系数的大小影响抛物面内的热传导过程和温度均匀性。相同条件下,导热系数越大,抛物面整体温度越低,同时,下表面的温度差减小,表面和径向温度分布更均匀。
在后续的研究工作中,将进一步考虑抛物面天线导热系数的各向异性以及外热流的非均匀性等参数对其热平衡与热变形特性的影响规律。
