基于贝叶斯优化的SVM-Xgboost移动支付风险预警模型

李保安, 张雨祺，李培峦

(1.河南科技大学 数学与统计学院, 河南 洛阳 471023；2.洛阳职业技术学院，河南 洛阳 471000)

0 引言

作为互联网信息技术所衍生的新兴产物，移动支付具有高效、快捷、便携、便利等优势，给人们的生活带来了便捷，也推动着社会经济和其他行业的进步。但同时，移动支付的发展过程也产生了政策风险、法律风险、资金安全风险等诸多问题，这些问题均可能对用户造成资金损失，因此，寻找一种能够对移动支付交易记录进行风险侦测的方法至关重要。

由于移动支付仍属于较新事物，故相应研究文献相对较少。文献[1]基于粒子群算法优化对支持向量机(support vector machine,SVM)进行改进，用于对电子商务移动支付风险进行预测。文献[2]使用层次分析法对农村移动支付风险因素进行了研究分析。文献[3]提出使用数据挖掘相关技术，对多维电子商务移动支付风险的时间序列进行分析，构建了预测模型。文献[4]先使用威胁模型(spoofing tampering repudiation information disclosure denial of service elevation of privilege，STRIDE)建立指标体系，再使用模糊综合评价法对移动支付交易进行风险评估。文献[5]对移动支付存在的风险进行分类并确定权重后，使用反向传播(back propagation，BP)神经网络对移动支付的整体风险评价程度进行了预测。文献[6]以银联手机闪付为例，将各种风险分类后，使用层次分析法建立各级指标体系，并使用内容效度比进行指标检验，最后建立了神经网络进行训练验证和风险预测。以上对于移动支付风险研究多是从移动支付本身存在的风险因素进行研究分析，而对于移动支付交易记录存在的风险侦测相关研究较少。

极端梯度提升树(extreme gradient boosting，Xgboost)算法属于Boosting集成，是基于传统梯度提升算法的改进，具有防止过拟合效果好、运算速度快、效率高等优势，近年来应用广泛，发展良好，不少学者对其进行了改进。文献[7-8]使用随机森林对Xgboost算法进行了改进，使其在回归预测上的精度得到了提升。文献[9]使用改进网格搜索调参改进Xgboost算法用于个人信用评估。文献[10]使用粒子群优化改进Xgboost模型用于高速公路服务区交通量的预测，预测性能得到提升。文献[11-12]使用代价敏感激活函数改进Xgboost算法用于处理不平衡数据分类方法，增强了Xgboost算法对不平衡数据的处理能力。文献[13-15]利用贝斯优化Xgboost调参提高其预测性能。综上，大部分对于Xgboost算法的改进是使用不同的优化算法对其寻参调整的改进，且仍存在一定的不足，如在利用遗传算法和随机森林对Xgboost算法改进时，使用遗传算法对两模型权重进行优化的过程中。以均方误差为目标函数,未兼顾到其他评价指标[7];使用代价敏感激活函数对Xgboost算法进行改进用于处理不平衡数据分类方法时，对误分类代价的设置过程进行了简化，但导致了模型性能的下降[11]。

SVM作为传统的机器学习算法，已有相当多的研究和改进，文献[16-18]均是对SVM进行参数寻优等改进，提高其预测准确率后应用于解决各种问题。另外，贝叶斯优化是机器学习中常用且较好的调参方法，具有比传统网格搜索更快的运行速度及性能，已有研究使用贝叶斯优化对Xgboost[13-15]、极限学习机[19]、LightGBM[20]模型调参优化，优化后的模型预测准确率都有较大幅度的提升。

为了解决现有技术的不足，综合上述模型及算法的优势，本文提出一种基于贝叶斯优化的SVM-Xgboost组合模型，用于移动支付交易记录风险侦测方法。该模型使用贝叶斯优化分别对SVM和Xgboost的参数组合进行寻优，再将优化后的两模型使用堆叠法进行组合。经验证，该组合模型预测性能较改进前的模型性能均有所提升，能够准确地对移动支付交易记录进行风险侦测。

1 基于贝叶斯优化的SVM-Xgboost组合模型

本文利用贝叶斯优化，将SVM算法与Xgboost算法进行组合,将两种不同的学习方法进行组合，可以结合两种方法的优点。

1.1 建立SVM模型

SVM是一种基于统计学习理论的通用算法，根据结构风险最小化原理进行建模，主要原理是根据数据分布，选择最大边缘化的超平面将数据分开，即两类数据中距离该平面最近的点到该平面距离最远的超平面。

具体过程如下：

步骤1：将数据集分为训练数据集和测试数据集。

步骤2：训练数据样本为(xi,yi)，共m个样本，其中，xi为第i个样本的属性集，yi为类别标号。设存在一个超平面可将样本分开，该平面可表示为：w·x+b=0，其中，w和b为模型参数。使用特征空间的φ(x)代替x，则可表示为w·φ(x)+b=0。

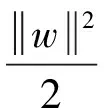
(1)

其中:σ为径向基宽度参数。

其对偶优化问题为：

(2)

(3)

步骤4：对该对偶优化问题求解，得最优超平面的w和b,即可得到SVM决策函数为：

f(x)=w·φ(x)+b。

(4)

1.2 基于贝叶斯优化的SVM模型

贝叶斯优化算法[21]利用贝叶斯优化原理，选择概率代理模型对目标函数进行拟合。

随机选择一组参数，将训练数据集代入该模型进行训练，并使用贝叶斯优化算法进行参数调整，得到基于贝叶斯优化的SVM模型,具体过程如下：

步骤1：本文选择树结构概率密度估计(tree structure probability density estimation,TPE)作为概率代理模型进行贝叶斯优化。

定义

(5)

p(c|q)即模型损失函数为q时超参数为c的条件概率，即后验概率。

首先，根据已有的数据选取一个损失函数的阈值c*；然后，对大于阈值和小于阈值的数据，分别学习两个概率密度估计t(c) 和u(c)。

步骤2：本文选择预期改进(expected improvement,EI)作为采样函数进行概率密度估计，并计算先验数据集中每个超参数的后验分布：

(6)

其中：q*=min{(c1,f(c1)),…,(ci,f(ci))}；p(c)为c的先验概率；p(q|c)为c的似然概率。

(7)

最大化采集函数，则u(c)/t(c)最小时，得到一个新的超参数值c**，将该值重新代入SVM模型中，再次拟合t(c)和u(c),选出最大EI值对应的超参数值，直到迭代结束，这里设置迭代次数为100次，最终选择100次迭代中SVM准确率最高的参数组合。

步骤4：将寻找到的最优参数组合记录下来，代入SVM模型中，可得到基于贝叶斯优化的SVM模型。

1.3 建立Xgboost模型

Xgboost算法是由文献[22]设计的，是基于传统梯度提升算法的改进。传统梯度提升算法基本原理是根据当前模型损失函数的负梯度信息来训练新加入的弱分类器，然后将训练好的弱分类器以累加的形式结合到现有模型中,得到最终预测模型。

具体过程如下：

步骤1：确定Xgboost模型迭代训练的目标函数为：

(8)

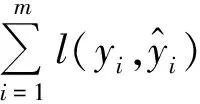
(9)

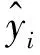
(10)

其中：Ω(fk)为第k棵树的模型复杂度；T为所建决策树的叶子数量;ω为所建决策树第j个叶子节点上的预测分数，也称作叶子权重；γ、λ为惩罚系数，默认γ=0、λ=1。

步骤2：训练模型，每一次迭代，就在目标函数中加入一个新函数，第t轮，则加入新函数ft(xi)，使得目标函数降低最多，故第t轮的目标函数为：

(11)

用泰勒公式展开取前3项，进行化简，最终化简结果为

(12)

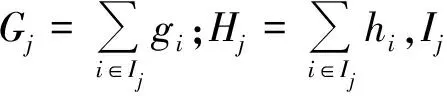
步骤3：求目标函数最小值，即对目标函数求偏导使其等于0，求出ωj表达式，并将其代入目标函数中，得目标函数表达式为：

(13)

根据表达式直接探索到最优树结构，即能够使目标函数降低最多的函数ft(xi)，并可求出最小值。

步骤4：最后，求得最终样本数据的预测值：

(14)

即每次迭代所得预测结果之和，由于采用逻辑回归的损失函数，故最终预测结果表示分类概率，为[0，1]的任意一个数。

1.4 基于贝叶斯优化的Xgboost模型

随机选择1组参数，将训练数据集代入该模型进行训练，并使用贝叶斯优化算法进行参数调整，得到基于贝叶斯优化的Xgboost模型，具体步骤与贝叶斯优化SVM相似，详细过程见1.2。

1.5 基于SVM-Xgboost的组合模型

采用堆叠法将两模型进行融合，建立基于SVM-Xgboost的组合模型，将训练数据集代入模型进行训练后，代入测试数据集，得到最终预测结果，具体模型融合过程如下：

步骤1：将上述两个模型在训练数据集上所产生的结果作为新的训练集,使用逻辑回归模型对其进行训练,也就是将上述两模型的答案作为输入，通过逻辑回归给上述两个模型的答案分配权重。

步骤2：将测试数据集导入上述两个模型，分别得到预测类别概率值，作为新的测试集。

步骤3：使用步骤1训练好的逻辑回归模型，将步骤2得到的特征值代入该逻辑回归模型，进行预测，得出最终测试集上的预测类别或概率。

算法具体流程图如图1所示。

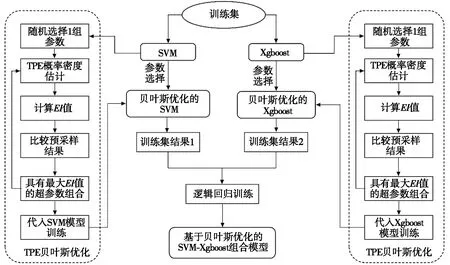
图1 算法流程图

2 实证分析

2.1 模型实验数据

实证数据集来源于kaggle平台，共有1 048 575条数据，其中1 142条数据有风险，类别标签为1，其余为无风险数据，类别标签为0。由此可知，该数据集比例极不平衡，但这与现实生活相符，因为移动支付风险交易为一类“小概率大风险”的事件。该数据集包含10个属性列，1个标签列，属性列包括时间、交易类型(X1)、交易金额(X2)、交易发起方姓名、交易前本金(X3)、交易后本金(X4)、交易接收方身份、交易前接收方本金(X5)、交易后接收方本金(X6)、单次交易是否超过20万(X7)、标签列为交易风险(Y)，具体类别变量及含义如表 1 所示。

表1 类别变量及含义

2.2 数据预处理

该数据集不存在缺失值和重复值，删除无关变量如时间、交易发起方姓名、交易接收方身份。由于该数据集中数据量充足，但出现风险的数据过少，数据极不平衡，故采用随机欠采样的方式对数据进行采样预处理，即随机删除大样本数据量，保留小样本数据，使得两类数据达到平衡，并将数据集的70%作为训练集，30%作为测试集。

2.3 建立模型

2.4 实验评价指标

将测试数据集代入建立好的基于贝叶斯优化的SVM-Xgboost组合模型中，进行检验，检验指标包括准确率、召回率、接受者操作特性(receiver operating characteristic,ROC)曲线及ROC曲线下的面积(area under curve,AUC)值。准确率表示预测正确的样本数占总样本数中的比例，召回率表示模型正确预测的交易记录存在风险的样本数占所有实际交易记录存在风险的样本数，AUC值为ROC曲线与X轴和Y轴在右下方围成的面积，该值越大则模型预测性能越好。具体计算如下：

(15)

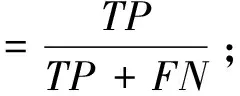
(16)

ROC曲线及AUC值。

其中：TP是实际为正样本且预测为正样本的样本数；TN是实际为正样本且预测为负样本的样本数；FP是实际为负样本但预测为正样本的样本数；FN是实际为正样本但预测为负样本的样本数。

2.5 实验结果对比与分析

分别运用训练好的未改进的SVM、贝叶斯优化的SVM、未改进的Xgboost、贝叶斯优化的Xgboost和贝叶斯优化的SVM-Xgboost对测试数据集进行预测，预测结果如表2所示，ROC曲线如图2所示。

表2 模型结果

由表2可知：基于贝叶斯优化的SVM-Xgboost组合模型的准确率为97.3%，该模型较单个模型在准确率上分别提升17.4%、0.8%，即模型分类预测的准确性有较大提升；召回率分别提升40.7%、3.0%，即样本中有风险的记录被预测正确的比率有较大提升；AUC值分别提升16.4%、0.8%，可见基于贝叶斯优化的SVM-Xgboost模型对于移动支付风险侦测具有良好性能。

图2 ROC曲线

ROC曲线如图2所示，图2中，横坐标为假正率，即预测为正的负样本数与负样本实际数之比；纵坐标为真正率，与召回率计算公式相同，表示模型预测正样本数占所有实际正样本数的比例。该曲线越靠近左上角则模型性能越好。由图2可知：基于贝叶斯优化的SVM-Xgboost模型ROC曲线更靠近左上角，性能更好。

3 结束语

本文通过建立基于贝叶斯优化的SVM-Xgboost模型对移动支付交易记录是否存在风险进行侦测，其中所使用的贝叶斯优化相较于传统的网格搜索和随机搜索效率更高，且具有不容易陷入局部最优的特点。Xgboost算法运行效率更高，泛化能力更强，且具有良好的防止过拟合效果。SVM是基于统计学习理论的通用算法，使用核技术，使其处理非线性问题功能强大，其算法结构简单，易于操作，3者进行结合，建立基于贝叶斯优化的SVM-Xgboost组合模型能够使三者的优势进行融合，得到更好的移动支付风险侦测模型，可以进一步改善预测效果。

该模型可用于移动支付领域交易风险的侦测，可以根据交易类型、交易金额、交易前本金、交易后本金等变量来推测出该笔交易是否存在风险，可以及时给予用户反馈提醒，提高用户警惕，及时追回支付金额，减少用户经济损失。