面向配送中心选址问题的改进型重心法

严毅　邓超　王有福　李艳淇　马俊杰

摘  要：选择合适的配送中心可以提高运输效率，选址问题的传统求解方法为重心法，随着物流业的发展，重心法劣势逐渐凸显出来，包括选址需求点位置坐标不能准确被获取，理论距离与实际距离误差较大，运费计算过程存在偏差。通过引入非直线系数解决了传统重心法理论距离与实际距离误差问题，以最小成本为目标提出一种改进型的重心法。采用改进型重心法使选址结果更加精准，成本节约5.06%，研究成果可为选址问题提供理论依据。

关键词：物流工程;配送中心;选址;最小成本;重心法

中图分类号：F252.14    文献标识码：A

Abstract： In order to choose the appropriate distribution center can improve the efficiency of transportation， the location problem of the traditional method is heavy loading， with the development of the logistics industry， the center of Gravity method location demand point coordinates cannot accurately capture， theory of distance and the actual distance error is larger， the freight calculation process there is a deviation， such as disadvantage highlighted gradually， with the minimum cost as the objective proposed a modified Gravity method， the error between theoretical distance and actual distance of traditional barycenter method is solved by introducing non-linear coefficient. The improved center of Gravity method is adopted to make the site selection result more accurate， and the cost of the example in this paper is reduced by 5.06%. The research results can provide theoretical basis for the site selection problem.

Key words： logistics engineering; distribution center; site selection; minimum cost; Gravity method

0  引  言

近年來，物流系统已经成为企业的第三利润源泉，而配送中心是物流系统的枢纽，配送中心的选址问题一直是影响物流系统发展的关键，其承接供应方和需求方，合理设置配送中心可以提高运输效率，降低物流成本。重心法是一种较实用的选址方法，其主要有两个优势：第一，原理简单，所用的数据较少;第二，具有连续选址的优点，选址过程所受的限制较少。王勇等[1]使用重心法来解决农村物流网点的位置问题;吴坚等[2]在选址上把遗传算法与重心法进行了对比;朱晓敏等[3]把重心法选址的优点作了深入讨论。由此可见，重心法是研究配送中心选址问题的主流方法。

然而该方法有几个问题：其一，各个需求点的位置坐标是人工确定的，既不方便又不准确;重心法假设运输距离为直线距离，理论距离与实际距离误差较大;运输量与运费通常为非线性关系，传统重心法计算运费计算过程存在偏差;不同地区配送中心的建设成本往往会随当地的政策、地价和交通情况而变化，传统重心法需求函数考虑的因素不够全面。国内外学者基于其他方法对配送中心选址问题进行了研究，赵韦等[4]描述了粒子群优化算法的求解过程，建立了一种配送中心成本服务模型;刘安业[5]以供应链管理思想为基础，分析了物流配送中心优化决策和车辆调度问题;凌晨捷[6]通过贪婪启发式模型研究配送中心选址问题;李昌兵等[7]基于层次分析法与遗传算法相结合的双层规划模型求解选址问题;Linda[8]基于混合0～1整数规划法分析了选址的影响因子，在多品种双层库存系统中针对单一产品仓库的选址问题提出了非线性混合整数规划模型;Steven[9]基于可接受的服务水平条件下，提出了逐次逼近的求解算法;胡刚等[10]建立了适用于第三方物流企业的选址线性规划模型。

1  模型的建立

重心法的基本原理是把各个物流需求点看作存在一个平面内的，再将每个需求点的需求量当作物体的质量，算出该物体系统的物理重心，即物流配送中心。重心法将待求点的位置坐标看成变量，放在平面直角坐标系中，然后表示出待求点与需求点之间的理论距离，再将该距离分别与需求量、运费相乘的乘积之和作为需求函数，计算出函数的最小值即可。建模的准备工作包括以下几个方面：

第1步：根据经验或者企业的要求，确定要进行选址的地区，初次确立的地区范围往往比较大，将其划分为更小的需求点，这个需求点要求精确到城市的某个区，统计这些需求点的个数。

第2步：运用地理信息系统查询每个需求点的具体经纬度坐标，选取合适的坐标原点建立平面直角坐标系。GIS技术隶属于地理信息系统，可以精准地得到某些地区的经纬度。将每个地点的名称输入地理信息系统，通过空间查询功能即可得到它的经纬度[11]。

第3步：确定各需求点对商品的需求量，确定各需求点运输该商品时需要的运输费用。运输费用一般都不固定，会根据其他的某些因素而产生变化，假设在某一段时间，商品的运输费用不会发生变化。

第4步：求初始解，假设在选址过程中，存在n个需求点，令这些需求点的坐标为^X，_Y，需求量分别为 Wi=1，2，3，…，n。待求的物流配送中心，最优位置坐标为^X，_Y;r为待求点到各个需求点i的运输费率，传统重心公式求得物流中心的初始坐标为^X，_Y。

X= （1）

Y= （2）

本文将传统方法进行优化，配送中心选址问题隶属于最小成本问题，这里考虑运量运输成本，配送中心的不变成本和可变成本。在传统重心法中，需求点i到待求点的距离是用直线来代替的， 由于这样误差比较大，所以引入非直线系数C，非直线系数能够将需求点i到待求点的直线距离d转换成运输距离D，与现实情况会更相近。

D=Cd （3）

d= （4）

总费用H的需求函数为：

H=W·D·r+S·μ （5）

S为物流配送中心的仓库面积，μ为物流配送中心单位建设费用和经营费用，将式（3）视为关于X和Y的二元函数，要使得H最小，必须满足：

==0 （6）

==0 （7）

可求得物流配送中心的坐标为：

X= （8）

Y= （9）

式（6）、式（7）中含有X和Y，在第4步中已经求出，直接代入即可。

第5步：通过迭代求得最优解。将求得物流中心的初始坐标X，Y代入式（1），计算出运输距离D和总费用H;将D代入式（4），求出改善后的物流配送中心坐标X，Y;重复以上计算过程，直到计算出的配送成本值变化非常小为止。

第6步：确立配送中心具体位置。经过几次迭代之后，将计算所得的坐标值，利用地理信息系统转换查询功能，能够找到该坐标值对应的实际位置。最后根据现实状况，决策者做出必要的调整。

2  模型应用

某公司生产工厂离销售市场非常远，长距离配送成本压力大，且该公司没有物流运输系统，产品的运输依靠与物流公司配合完成，产品时效性问题严重，导致缺货、断货和送货不及时的现象时有发生，难以满足客户需求。该公司拟通过设立京津雄区域配送中心来缓解工厂仓配压力，以更好地满足客户终端配送需求。依据前文提出的改进型重心法对配送中心选址问题进行求解。

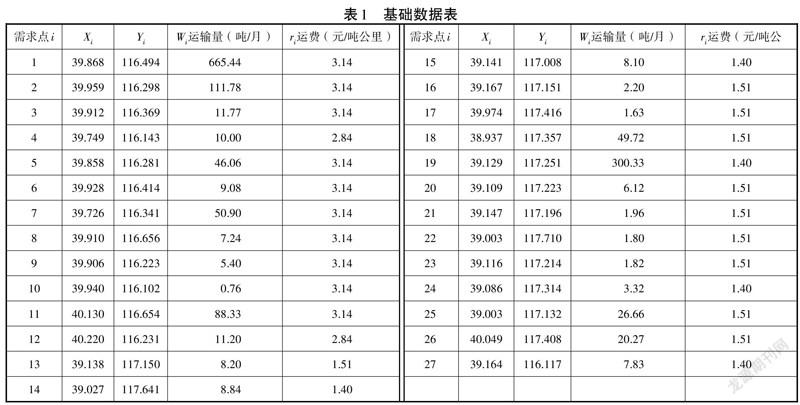
根据该公司在京津雄地区的客户订单特点，以区县级别进行划分为27个区域，每个区域作为一个需求点，统计每个需求点的需求量。因为在不同地区交通运输条件不同，运费有较大的差别，为计算简便，调用该公司的历史数据进行求解。基础数据如表1所示：

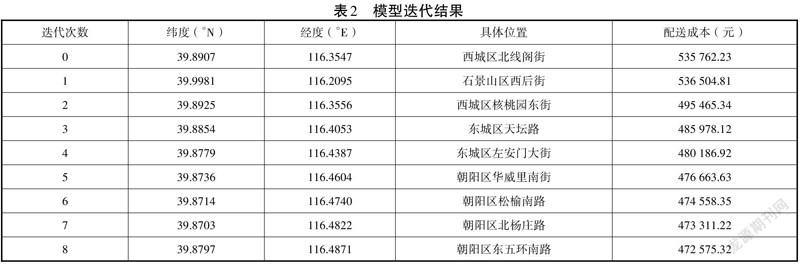
将得到的基础数据代入式（1）和式（2），用傳统重心法计算出初始解，得到的经纬度坐标分别为116.3547，39.8907，位于北京西城区西线阁街。通过查阅城市交通道路的非直线系数C，北京为1.4，天津为1.35，其他地区为1.3[12]。再将初始解代入式（3）、式（8）和式（9）进行迭代计算。物流配送中心的坐标及配送成本计算结果如表2所示。

经过8次迭代之后，配送成本的变化已经非常小，可以忽略不计，即得出需求函数的最优解所在位置，经度39.8797°N， 116.4871°E，用地理信息系统转换后，查询到最优的地址在北京东五环南路，该位置附近有北京马驹桥物流产业园，产业园交通便利，具有十分充足的仓储资源。

由于配送中心选址问题隶属于最小成本问题，所以比较总成本即可。在上述计算过程中，已经使用了传统重心法，该方法得到的最优解位于北京西城区北线阁街，此处的配送成本为535 762.23元，仓储成本为120 000元，所需的总费用为655 762.23元。而优化后的重心法得到的最优解位于北京马驹桥物流产业园，配送成本为472 575.32元，仓储成本为150 000元，所需的总费用为622 575.32元，成本节约5.06%。显然，优化后的算法总费用更低，该方法具有实际价值。

3  结  论

本文提出更为改进型的重心法求解配送中心选址问题，并对把改进型的方法与传统方法进行对比，结果表明，改进型的重心法提高了选址精度，节约物流成本。改进后的重心法具有以下几个优点：地理信息系统查询得到的经纬度相比于普通方法更准确，以此计算后的结果误差较小;考虑了不同地区的交通情况，引入了非直线系数，将待求点和需求点之间的直线距离改为了更接近现实的运输距离;目标函数加入了配送中心的可变成本和不变成本，考虑因素更为周全。然而，改进型的重心法输入变量较多，未来将研究相关参数获取方法。

参考文献：

[1] 王勇，韦俊，姜涛，等. 物流配送中心选址数学模型的研究和优化[J]. 科技资讯，2020（2）：1-2.

[2] 吴坚，史忠科. 基于遗传算法的配送中心选址问题[J]. 华南理工大学学报，2004（6）：3-4.

[3] 朱晓敏，张兆强，乔魏乾. 基于重心法与物流量预测的物流园区选址[J]. 物流技术，2011（4）：3-5.

[4] 赵韦，李文峰，梁晓磊. 基于粒子群算法的多配送中心选址研究[J]. 武汉理工大学学报，2012（6）：2-3.

[5] 刘安业. 基于供应链管理的物流配送中心选址与车辆调度优化[D]. 哈尔滨：哈尔滨工业大学（博士学位论文），2009.

[6] 凌晨捷. ZARA公司的中国配送中心选址问题研究[D]. 上海：上海交通大学（硕士学位论文），2014.

[7] 李昌兵，杜茂康，曹慧英. 基于层次遗传算法的物流配送中心选址策略[J]. 计算机应用研究，2012（1）：3-4.

[8]  Linda K N， Mark T. Integrating inventory impacts into a fixed-charge model for location distribution centers[J]. Transportation Research Part E， 1998（5）：3-4.

[9]  Steven J E， Russell D. The interaction of location and inventory in designing distribution on systems[J]. IIE Transaction， 2000（3）：4-6.

[10] 胡刚，王淑琴，李铁柱，等. 针对第三方物流企业的物流配送中心选址模型[J]. 公路交通科技，2002（4）：4-9.

[11] 张建勋，韩宝明. 一种改进的区域物流配送中心选址方法[J]. 物流科技，2007（1）：9-12.

[12] 易华，张文杰. 北京市配送中心的选址研究[J]. 北京交通大学学报，2006（5）：5-7.