基于连续反演算法的时滞补偿控制综述

马永浩，张 爽，何修宇，刘志杰

1) 北京科技大学人工智能研究院，北京 100083 2) 北京科技大学自动化学院，北京 100083 3) 北京科技大学顺德研究生院，佛山 528399

时滞系统，通常称之为具有后效应或停滞时间的系统[1]. 相别于一般系统，时滞系统的一个本质特征是它的未来发展取决于系统的当前状态和过去状态. 时滞特性不可避免地存在于许多实际工程中[2]，例如：电力系统[3]、网络传输系统[4]、航天飞行器[5]、化学反应过程[6-7]. 时滞特性产生的主要原因是在系统信息获取、传输以及控制决策、执行等过程所需耗费必要的时间. 以常见的反馈控制系统为例，部件的物理结构限制或采集信号和控制信号的长距离传输等因素会导致传感器到控制终端和控制终端到执行器等通道上存在时滞现象. 而在网络控制系统中，在系统输出、控制输入等信息在系统组件(传感器节点，控制器节点，执行器节点等)间的交换过程中，通信网络媒介的引入会不可避免地产生滞后现象，导致系统具有时滞特性. 时滞现象的存在通常会影响系统的动态性能，如系统的响应时间和操作精度，甚至会导致系统的不稳定. Datko等指出任意小的时滞都能导致一维双曲型偏微分方程(Partial differential equations, PDEs)不稳定[8-9]. 因此，时滞系统的研究具有重要的理论意义和实际应用价值，是数学、控制等领域的热点研究问题之一. 针对时滞系统的研究由来已久，并取得了丰硕的研究成果[10-14]，其中，在无穷维系统中也具有广泛且深入的研究，如波方程[15]和薛定谔方程[16].

目前，常见的时滞补偿控制方法主要有：Smith预估控制[17-18]和有限谱配置法(Finite spectrum assignment, FSA)[19-21]等. Smith预估控制通过引入Smith预估器，将时滞部分有效地转移到了闭环控制之外，即消除了闭环传递函数的特征方程中存在的时滞特性，处理后的系统可按常规的控制器设计方法来设计，该方法的优点在于将含有时滞特性的设计问题转化为不含时滞特性的设计问题，使问题得到简化. 然而，该种方法严重依赖准确的数学模型，一旦模型和对象不匹配，Smith 预估器就无法得到理想的性能，甚至可能导致系统的不稳定. 另外，Smith 预估器对时滞参数非常敏感. 那么，Smith预估器只适用于非滞后部分稳定的输入时滞系统，对非滞后部分不稳定的情形却无能为力. 有限频谱配置法首先预估出一个超前的状态（超前量恰好等于输入滞后的时长），然后将得到的超前状态用于反馈，以便补偿输入滞后的影响，从而保证闭环系统是有限维的，这个维数恰好就是原系统的维数，并在此前提下实现全部特征值的任意配置. 该方法存在一个显著的不足：在闭环系统的稳定性分析中，合适的Lyapunov-Krasovskii函数的选取存在很大的难度，因为整个闭环系统包括有限维的系统状态和无限维的执行器状态. 为了克服这一不足，Krstic和Smyshlyaev研究了具有单输入时滞特性的有限维系统，创新性地引入分布式状态向量来描述执行器的状态，采用一阶双曲型PDEs表示系统中的时滞特性，将具有时滞特性的原系统映射为不具输入时滞特性的ODE-PDE级联系统，并引进连续反演算法降低Lyapunov-Krasovskii函数构造的难度[22].

本文尝试对基于连续反演算法的时滞补偿控制思路进行简洁的阐述，并针对其近年来的研究成果展开详细的介绍及分析，探讨时滞补偿控制的未来发展方向.

1 时滞系统分类

目前，根据时滞特性在系统中出现的不同位置，时滞系统主要可分为输入时滞系统、输出时滞系统、状态时滞系统等. 下面将简要介绍这三类时滞系统.

通常情况下，状态时滞系统仅部分状态量存在时滞现象. 特别地，针对具有部分状态时滞特性的系统，可直接在原系统上应用连续反演算法，而不需要采用双曲型PDE描述系统中的状态时滞特性.

2 基于连续反演算法的时滞补偿控制方法概述

在文献[28]中，Smyshlyaev和Krstic提出了面向PDEs的反演法. 该方法是针对PDE系统构造边界控制器和观测器的特定工具[29-31]，在处理ODE系统和PDE系统的时滞补偿特性时都具有它的独特优势. 以有限维系统为例，基于连续反演算法的时滞补偿控制方法的主要步骤如下：

步骤一

引入分布式状态向量描述时滞特性可获得ODE-PDE级联系统，如系统(5)和(8). 针对ODEPDE级联系统，通过增加或移除特定的附加项后得到期望的稳定目标系统. 具有输入时滞或输出时滞特性的目标系统表达式如式(11)所示：变换，得到相对应的时滞补偿控制律.

3 面向输入时滞的基于反演法的时滞补偿控制

由于系统控制决策的创建和执行通常需要一定的处理时间和响应时间，时滞特性在实际系统的输入部分非常常见. 近年来，基于连续反演算法的时滞补偿控制方法在处理时滞系统的已知和未知输入时滞特性过程中，取得了良好的时滞补偿效果和控制效果[32-34].

3.1 面向时滞大小已知的时滞补偿控制

针对输入时滞已知的情况，Krstic与Smyshlyaev首次将连续反演算法应用于具有单输入时滞特性的ODE系统. 文中结合李雅普诺夫直接法提出了具有指数稳定性的目标系统，通过构造合适的反演变换函数和逆变换函数证明原闭环系统的稳定性[22]. 基于上文的研究，Krstic进一步分析了系统初始值对系统稳定性的影响[35]，并提出了具有逆最优特性的预测反馈控制律[36]. 不同于已有研究结果[23]，上文在控制设计中构造了一个低通滤波器，该控制律能够保证小时滞非匹配(Delay mismatch)情况下系统的指数稳定性，提升了系统的鲁棒性. 特别地，针对具有时变输入时滞特性的ODE系统，即 φ =d(t)，所引入的一阶双曲型PDE方程也具有时变特性，其对应反演变换函数的核函数也是时变的. 因此，证明闭环系统的稳定性时也需要构造时变的李雅普诺夫函数[37].

Tsubakino等面向具有多输入时滞特性的ODE系统，针对每个输入具有不同时滞大小，需对应引入具有不同空间域的描述时滞特性的一阶双曲型PDE方程. 进一步，文中针对获得的ODE-PDE级联系统构造了面向PDEs的类反演变换函数(Backstepping-like transformation)，并分析了系统的稳定性[38]. Bekiaris-Liberis和Krstic针对具有多输入分布式时滞的ODE系统，引入了面向PDEs的前馈-反演变换(Forwarding-backstepping transformation)，将原系统变换为期望的稳定目标系统，并结合二次型李雅普诺夫泛函证明了目标系统的指数稳定性；通过求解变换过程中变换函数和逆变换函数证明原系统的稳定性[39]. 在文献 [40-42]中, 作者进一步针对具有时变单输入时滞线性系统、定常多输入时滞线性系统和定常单输入时滞非线性系统研究了系统的逆最优特性.

Krstic针对具有输入时滞特性的反应-扩散PDEs系统，利用变量代换将具有时滞特性的原PDEs 系统映射为不具有时滞特性的PDE-PDE级联系统. 文中结合反演法设计了时滞补偿反馈控制，并给出了闭环系统精确的解析解[43]. Gu和Wang在文献[43] 的基础上进一步考虑了输出跟踪问题，利用连续反演算法，可以将PDE-PDE 级联系统映射为目标误差系统，该目标系统是以规定的速率指数收敛，在映射过程中可以得到对应的状态反馈控制器[44]. Qi等将时滞补偿控制方法进一步拓展到具有输入时滞特性域内分布式控制器的反应-扩散PDE系统[45]. Liu等指出，文献[22]所提出的时滞补偿控制不适用于无穷维系统，因为当系统为无穷维时，算子为无界算子[46]. 即使控制输入属于控制空间，经过算子的作用，也可能不在状态空间里. 针对该问题，Liu等提出了一种新的可逆反演变换，利用伴随理论得到所对应的时滞补偿控制律，使得具有输入时滞的无限维系统稳定. 此外，作者将历史函数向量的 约束条件从文献[43]中的 h ∈H1(-D,0;Hu)扩展到 h ∈L2(-D,0;Hu). Krstic研究了具有输入时滞特性和抗阻尼效应弦系统的时滞补偿控制[47]. 不同于反应-扩散PDE 方程，弦系统的最高阶导数为2阶，描述系统时滞特性的分布式状态量属于空间. 针对弦PDE系统的时滞补偿控制设计则具有很大的挑战性.

上述文章中提出的控制策略都是边界控制，与分布式控制比较具有一定的优势，如工程上较易实现. 然而，针对时滞分布参数系统，由于边界控制器的设计需要系统过去时刻的状态量，属于无穷维控制器，在实际系统中实现具有一定的难度.

3.2 面向时滞大小未知的时滞补偿控制

上述文献中针对系统中时滞失配的问题，提出了具有逆最优特性的时滞补偿控制方法，然而仅考虑了系统中小时滞失配的情况. 在很多实际系统中时滞特性的精确值是难以获得的，针对未知时滞大小系统的时滞补偿控制是亟需解决的问题. 近年来，将连续反演法与自适应相结合，在不确定时滞系统的未知时滞补偿控制方面取得了较为丰硕的研究成果[48-51].

Krstic和Bresch-Pietri针对具有未知输入时滞的不稳定ODE系统，首次提出了基于全状态反馈的自适应时滞补偿控制方法[52]. 不同于处理时滞大小已知的情况，该论文结合转换函数w(x,t)=U(t+D(x-1))将原系统转换为ODE-PDE级联系统. 该转变函数有利于获得与定常时滞大小相关的线性PDE方程，具体的表达形式如式(14)所示：

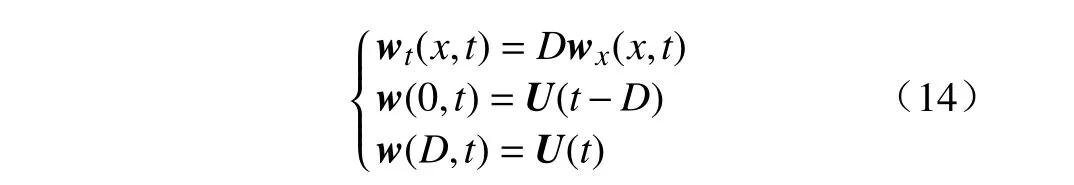
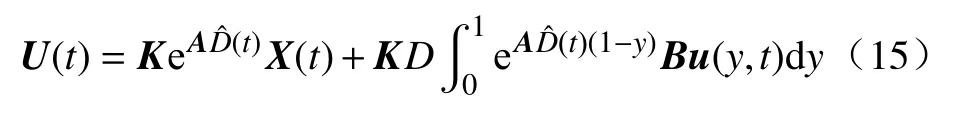
不同于处理离散输入时滞特性，处理分布式输入时滞特性的难点在于：分布式控制矩阵可能包含未知函数或未知参数. 为解决输入时滞特性和分布式控制矩阵的不确定性，文献[56]结合基于参数减少的参数变换(Reduction-based change of variable)和前馈反演变换方法求得对应的目标系统，控制率和更新率，以及针对该系统提出相应的自适应控制.

4 面向输出时滞的基于反演法的时滞补偿控制

输出时滞是输入、输出、状态三类时滞特性中较为容易处理的一种时滞特性. 处理该时滞的总体思路是通过构造合适的观测器获得当前时刻系统状态的近似值，以证明误差系统是收敛的.Krstic和Smyshlyaev面向具有定常输出时滞特性的ODE系统，通过参数变换求得ODE-PDE 级联系统，并提出了一种新型观测器来估计原系统的未知状态量[22]，如式(16)所示：

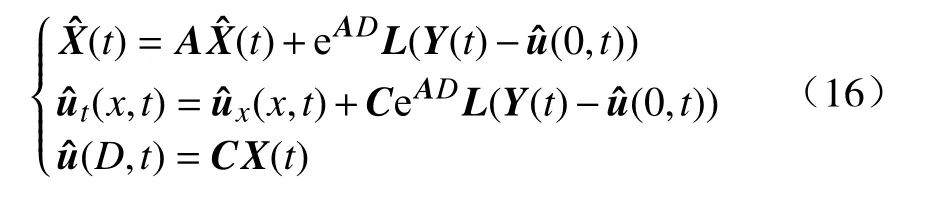
结合实际系统和观测器所得的误差系统，进一步利用反演变换方法将误差系统映射为预设的稳定目标系统，从而分析构造观测器对实际系统的精确跟踪性能. 与传统的仅估计系统状态的输出时滞补偿观测器[57-58]相比，该文所设计的观测器是一个全状态观测器，不仅估计系统状态，还估计传感器状态. Sanz等将该观测器的设计思路拓展到具有输出时变时滞特性的线性时变系统的时滞补偿控制研究中[59]. Wang等面向具有时变输出时滞特性的矿用电缆升降机系统，设计了一个全状态观测器，并结合连续反演算法获取了PDE-ODE-PDE级联系统[60]. 特别地，该论文采用两次反演变换所得到的描述目标系统特性的PDEs均为一阶双曲型类型，并保证了时滞状态PDEs和ODE之间的相互耦合关系转变为级联关系. 文献[61]研究了具有定常输出时滞ODE-PDE-ODE双曲型系统，利用末端ODE系统具有时滞的输出状态构造一个全状态观测器，进一步利用频域分析法和连续反演算法设计基于观测器的输出反馈控制策略.在该控制策略下，系统指数收敛. Pinto等结合连续反演算法与滑模控制，解决了具有时变输出时滞特性和未知外界扰动的线性时滞系统的稳定性问题[62].

然而，文献[22]和[59]所设计的观测器存在一个明显的缺点：无法处理充分大的输出时滞特性. 为了有效解决输出时滞系统中的大时滞问题，文献[63-64]提出了一种新的观测器，即链式观测器. 链式观测器的总体思路为：设定大输出延时为D秒，则链式观测器构造了m个子观测器，其中，每个子观测器包含一个预测器来预测总大输出延时中D/m秒内系统的状态量. Ahmed-Ali等结合链式观测器与类反演变换方法提出了基于PDEs的新型观测器，有效解决了具有任意大输出时滞非线性定常系统的状态估计问题和稳定性问题[65].

5 面向状态时滞系统的基于反演法的时滞补偿控制

Hashimoto等首次将连续反演算法应用于具有部分状态时滞特性的反应-扩散方程中[28]. 不同于处理输入、输出时滞特性，处理部分状态时滞特性，不需要采用一阶双曲型PDE方程来描述状态时滞特性，而是直接采用Volterra 映射将原系统变换为期望的目标系统. 进一步地，该论文采用了半群理论和Lyapunov-Razumikhin来分析目标系统的稳定性. Kang和Fridman采用连续反演算法来处理具有部分状态时滞特性的带Neumann-Dirichlet边界条件的反应-扩散方程[66]. 该论文还同时考虑了输入饱和特性，并利用Halanay不等式和Lyapunov直接法来证明了闭环系统的指数稳定性，给出了原系统吸引域的精确界值，进一步给出了保证目标系统稳定的LMI（Linear matrix inequality, 线性矩阵不等式）条件，该条件是与时滞大小相关的. Kang和Fridman面向具有状态时滞特性的线性[67]和非线性[68]薛定谔方程，采用连续反演算法提出了相应的边界约束时滞补偿控制律.

6 未来发展趋势

总体而言，基于连续反演算法的时滞补偿控制方法证明简单，易于获得闭环系统精确解等. 然而，相关的研究主要集中在ODE系统，PDE系统的相关研究还是很少，特别是时滞大小未知的研究，如表1所示. 连续反演算法的时滞补偿控制方法仍然存有很多问题有待进一步的研究：

表1 目前PDE时滞补偿控制研究内容Table1 Current research content of PDE time-delay compensation control

(1) 目前，针对时滞特性的研究主要集中于解决某种单一的输入时滞、输出时滞以及状态时滞特性. 然而针对两种或三种时滞耦合的研究很少.因此，针对多种时滞特性同时存在的时滞补偿控制设计也有待进一步研究. 多种非线性特性同时存在的相关研究[69]能够给该方面的研究提供一点启示.

(2) 基于反演法的自适应时滞补偿控制研究主要集中在ODE系统，然而针对PDE 系统的自适应时滞补偿控制仍处于空白阶段. 基于连续反演法针对时滞大小未知的PDE时滞系统的自适应时滞补偿控制研究是未来发展的重要方向之一. ODE系统自适应时滞补偿控制[52]和传统的PDE系统的自适应控制[70]均可为PDE时滞系统的自适应时滞补偿控制研究提供策略借鉴.

(3) 基于反演法的时滞补偿控制的研究对象局限于抛物线型的反应-扩散方程，然而针对其他类型分布参数系统的相关研究几乎没有. 主要是因为，以抛物线型的反应-扩散方程为代表的抛物线型方程的时间偏导数为一阶，该类型方程的大部分特征根都位于实轴，而波方程等双曲线型方程的时间偏导数则是二阶，它们的大部分特征根都位于虚轴，导致可逆变换的设计难度增加. 将基于反演法的时滞补偿控制拓展于双曲线型分布参数系统的时滞补偿控制研究也是未来发展的重要方向之一. 通过变量代换，可以将二阶的方程变换为两个级联的一阶方程[71]，这为双曲线型方程的研究提供了一个思路.

7 结束语

本文基于连续反演算法的时滞补偿控制方法的基本原理进行概述，并从输入、输出和状态三类时滞特性的时滞补偿控制的最新进展进行了简单的阐述和评价. 虽然基于连续反演算法的时滞补偿控制研究取得了一系列丰硕的成果，但是存在时滞类型单一，研究对象局限于基本的数学方程等问题，缺乏对仿生扑翼飞行器[72-74]、多旋翼机[75]和加油机软管[76]等实际系统的时滞补偿控制研究，如何设计有效的基于连续反演算法的时滞补偿控制方法，降低实际分布参数系统的时滞特性的影响是未来的研究方向.