剪力柔性梁格法在π梁斜拉桥中的应用研究

宋文锋，庞芝炯

(重庆中煤科工工程技术咨询有限公司，重庆 400042)

0 引言

有限元法是目前应用最广的斜拉桥分析方法，且具有计算方便快捷、精度较高，同时可以与规范衔接，因此可满足桥梁结构的力学行为分析研究。由于不同的有限元建模方法有不同的特点，因此在利用有限元方法对斜拉桥结构进行力学行为分析时，需要根据精度和需要解决的问题选择模型离散。结构有限元建模一般分为以下四种方法：单梁法、梁格法、板壳单元法和三维实体单元法。梁单元法无法得到内力的横向分布，板壳元法和实体元法模型复杂，计算费用高，数据处理烦琐；梁格法因其计算方便、费用经济，在工程分析中广泛应用。

1 梁格理论

1.1 梁格法

梁格法是E.c.Hambly[1]提出的一种简便实用的分析方法，把复杂结构模拟成一个纵、横交叉的空间梁格体系，其力学模型符合结构的实际受力情况，可以直接得到结构的内力与变形，即考虑了荷载作用下结构沿纵向产生的弯曲和整体扭转，还考虑了整个截面的横向变形，为斜拉桥π梁结构分析计算提供了一种较实用的理论方法。

1.2 梁格法基本原理

将实际结构的刚度(如抗扭刚度和弯曲刚度等)用梁格刚度等效代替，在相同荷载下挠曲线相同，因两者结构特性上的差异，等效梁格的内力近似等效实际结构的内力[2]。梁格法建模的关键：

1)等效梁格与实际结构纵向弯曲等效，横向梁格中性轴与实际结构同一高度。

2)梁格刚度与实际结构刚度等效，同时对纵、横向梁格的剪切面积和抗扭惯性矩进行修正。

π梁断面采用双纵梁式模型，在梁格力学模型简化时，边梁的面积和抗弯刚度与实际结构等效性，且竖向抗弯刚度提供的约束扭转刚度与实际结构等效性[3]。

2 工程概况

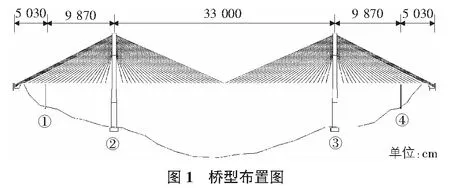
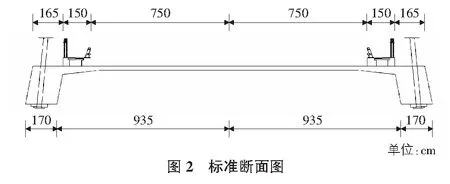
某特大桥桥跨布置为(149+330+149) m浮体系PC斜拉桥，边跨距索塔中心线98.7 m处设置辅助墩如图1所示，主梁采用C50预应力混凝土π梁，梁高2.3 m，板厚0.25 m，纵肋底部宽1.7 m，梁顶部全宽21.3 m，底部全宽22.1 m，每6 m设置一道0.25 m的横隔梁；索塔为倒Y型，采用C40钢筋混凝土及预应力钢筋混凝土箱形截面，塔高121.5 m，其中上塔柱高33 m、下塔柱高55.5 m、中塔柱高33 m；斜拉索采用扇形布置，共计212根，边跨与中跨各设52对拉索，除边跨最外端4对拉索间距为0.7 m外，其余斜拉索索距均为6 m，同时在塔中设置了1对外拉索，斜拉索采用φ7镀锌钢丝，标准强度1 600 MPa；桥面宽：1.5 m人行道+15 m车行道+1.5 m人行道=18.0 m，如图2所示。大桥设计荷载为汽车-超20级、挂车-120，人群-3.5 kN/m2。

3 挠度、应变控制截面测点布置

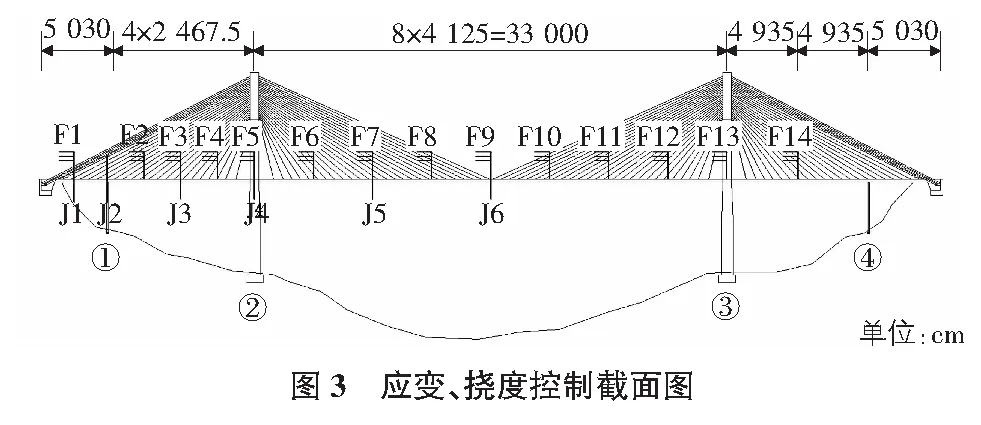
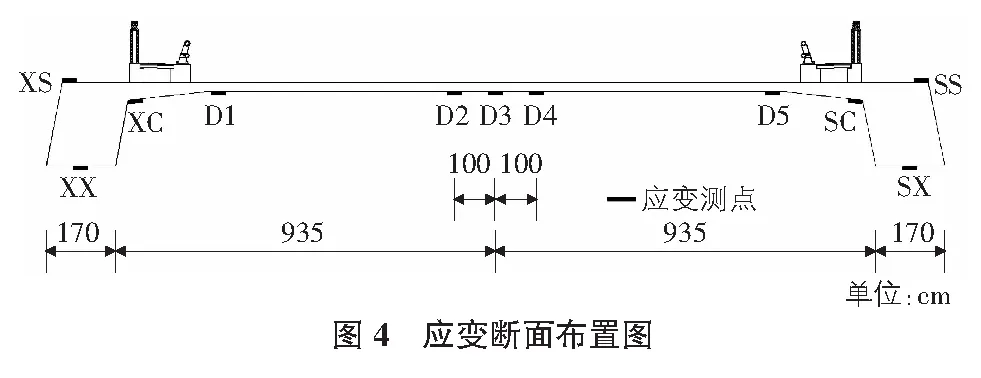
根据斜拉桥的受力特点确定桥梁的内力和挠度控制截面，通过控制截面的实测值以验证剪力柔性梁格法计算分析斜拉桥的准确性，实用性。应变控制截面划分如下：左侧边跨跨中截面J1、辅助墩中心1.4 m截面J2、次边跨跨中截面J3、主塔中心截面J4、主跨L/4截面J5、主跨跨中截面J6；挠度控制截面为F1～F14，如图3所示，控制截面的断面布置如图4所示。

4 结构有限元模型

为了验证剪力柔性梁格法的双纵梁应用在π梁斜拉桥上的精确程度，梁格法模拟如下：

1)纵横向梁格：将π梁对中划分近似实现“共同中性轴”的纵向梁格，并在每个节段交界处设置虚拟横梁，同时对在0号块处和桥台处应加密梁格。

2)索塔采用空间梁单元，截面与实际索塔截面相同，且索塔横梁采用共节点或刚性连接模拟。

3)斜拉索采用只承受拉的桁架单元模拟，拉索与主梁及主塔均采用刚性连接[4]。

4)边界条件：索塔、辅助墩采用一般支承中的固结模拟，桥台处4个盆式支座，采用一般支承模拟，主塔及辅助墩处2个盆式受压支座采用弹性连接。

根据以上梁格模拟原则，依托工程采用空间有限元分析软件Midas Civil建立全桥结构有限元模型如图5所示，主梁采用双纵梁梁格模型，其中836个纵梁单元和419个横梁单元；斜拉索采用受拉桁架单元，共212个；索塔和辅助墩采用梁单元，共160个。

5 理论与实测结果分析

根据控制截面的弯矩等效及内力影响线布载的原则，确定试验荷载，全桥共设6个工况，分别为J1，J2，J3，J4，J5，J6，以验证结构有限元模型的准确性。

5.1 主梁应力对比分析

在试验荷载作用下实测π梁的应变，并根据弹性模量将应变转换为应力，同时对实测值与理论值进行分析对比，以验证剪力柔性梁格法计算π梁斜拉桥的精确性及实用性。各工况试验荷载作用下的应力增量如表1所示。

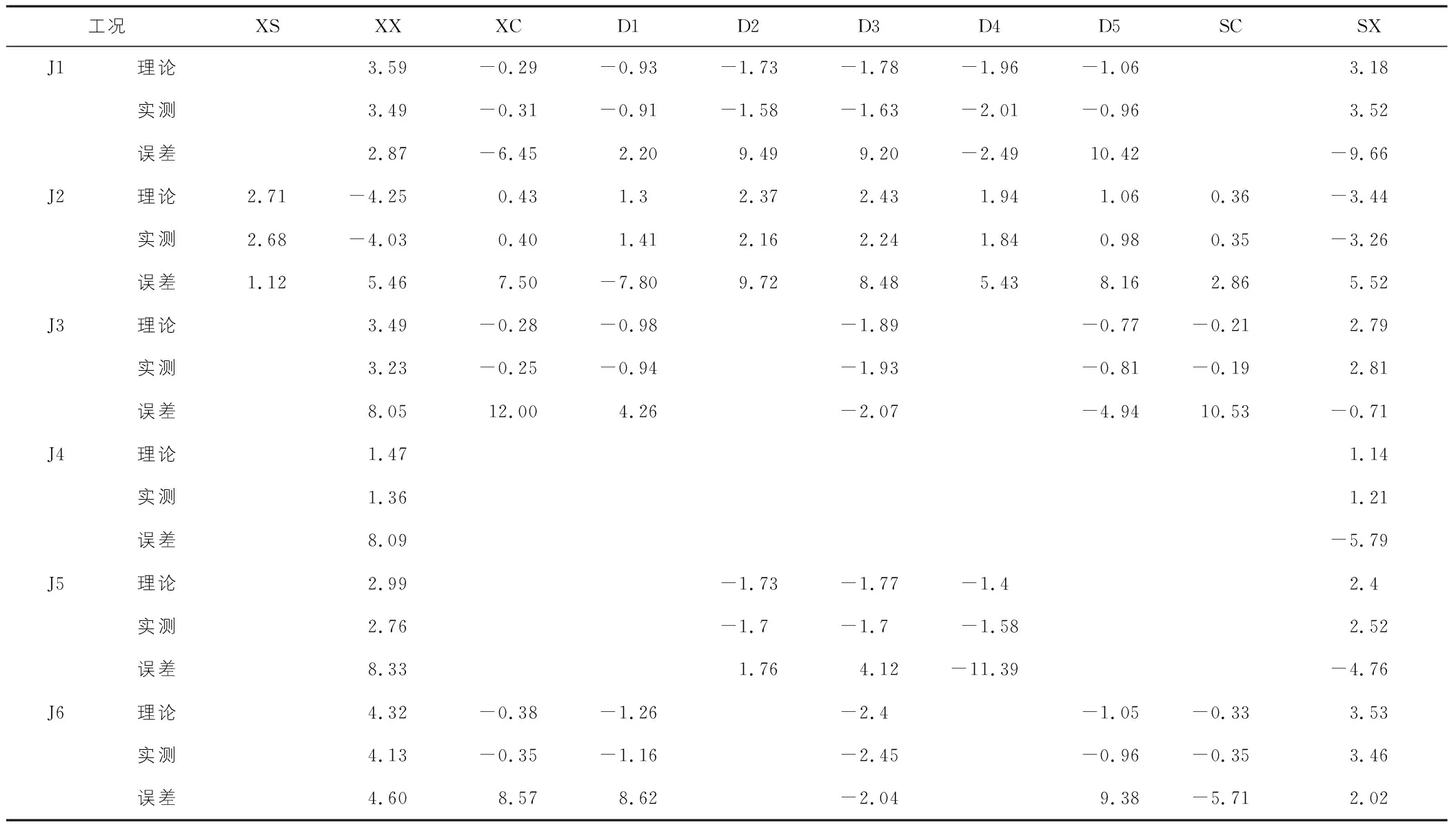
表1 试验荷载作用下混凝土应力 MPa

通过以上对比分析可知：梁格模型的计算结果可以准确地反映出试验荷载作用下斜拉桥π梁的正应力分布，且理论较接近实测值，最大误差仅11.39%，同时也验证了双纵梁模型影响线的准确性及可靠性。

5.2 主梁挠度分析

在试验荷载作用下对π梁挠度的实测值与理论值进行分析对比，也是验证剪力柔性梁格法精确与否的最基本原则之一。各工况试验荷载作用下的挠度增量见表2。

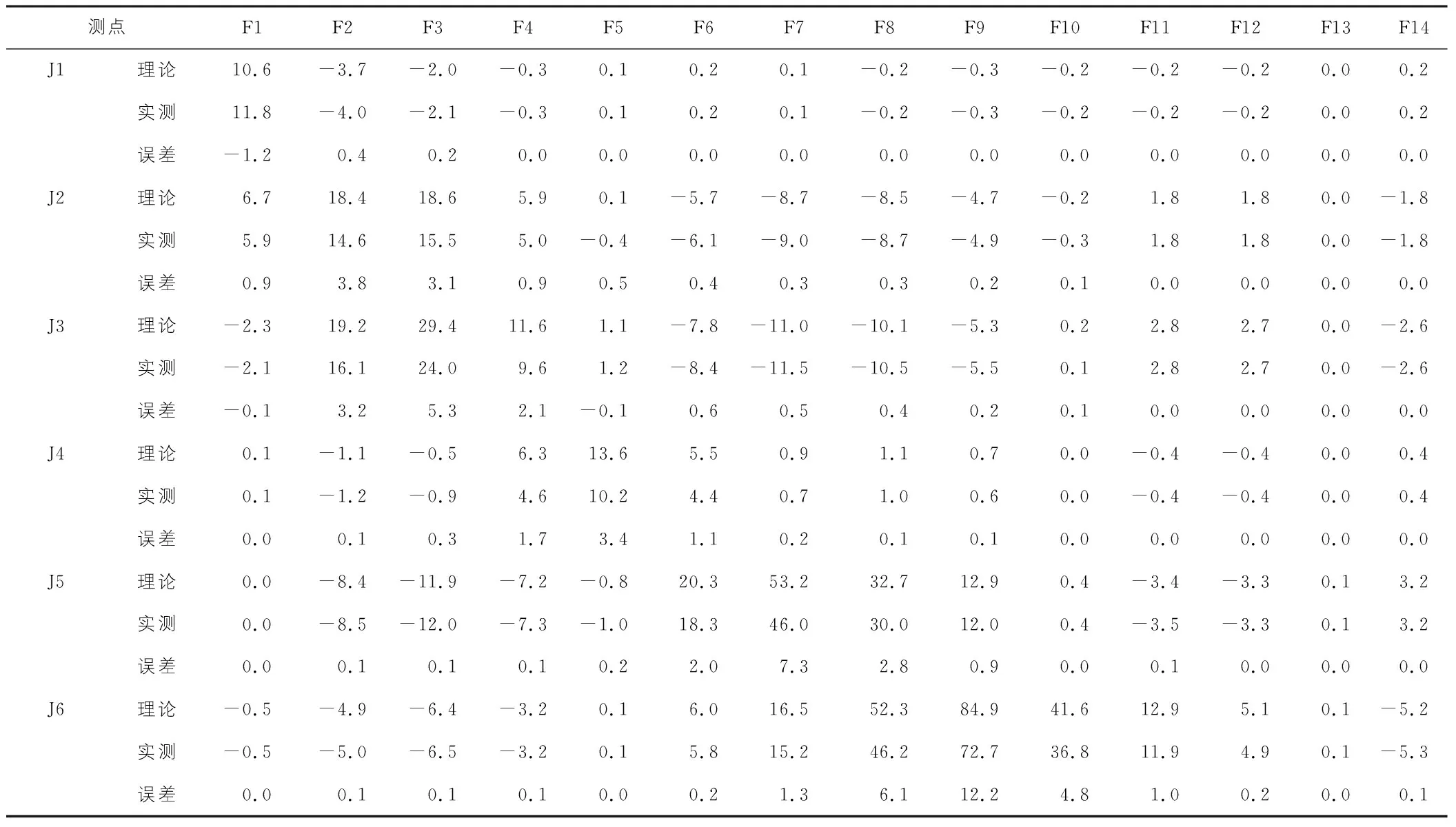
表2 试验荷载作用下桥梁挠度 mm

通过以上挠度对比分析可知：双纵梁梁格模型的计算结果可以准确地反映出试验荷载作用下斜拉桥π梁的挠度变化，且理论较接近实测值，最大误差仅12.2 mm，验证了剪力柔性梁格法在π梁斜拉桥计算中的合理性，为同类斜拉桥的结构力学行为分析提供借鉴[5]。

6 结语

通过剪力柔性梁格法对依托工程进行有限元结构分析，并根据控制截面弯矩等效及内力影响线布载的原则，确定试验荷载，最后通过试验荷载作用下的理论值与实测值进行分析对比，得出如下结论：

1)双纵梁梁格模型的计算结果可以准确地反映出试验荷载作用下斜拉桥π梁的正应力分布及挠度变化，且理论较接近实测值，应力最大误差仅11.39%，挠度最大误差仅12.2 mm。

2)π梁对中划分近似实现“共同中性轴”的纵梁及每个节段交界处设置虚拟横梁的梁格模型可满足π梁斜拉桥受力分析的工程精度要求。

3)双纵梁结构的内力影响线与依托工程的结构内力影响线基本相符。

4)剪力柔性梁格法的双纵梁模型可以准确地把握π梁斜拉桥的力学行为，计算结果安全可靠，为类似π梁斜拉桥结构的力学行为分析提供参考。