铁路集装箱客车化开行停站方案与箱位预分综合优化模型研究
2022-05-25谢旭申
赵 娟 ,刘 畅,谢旭申,卫 刚
(1.北京交通大学 交通运输学院,北京 100044;2.中国铁路经济规划研究院有限公司 运输研究所,北京 100038;3.中国铁路北京局集团有限公司 货运部,北京 100860;4.中国铁路设计集团有限公司生产经营中心,天津 300308)
1 概述
提高铁路货运竞争力,吸引货物运输“公转铁”是落实国家运输结构调整的重要举措。根据前期市场调研,铁路相对公路在货物运输时效性方面缺乏优势。因此,在将成本控制在一定范围的前提下,提高铁路货运的时效性是提高铁路货运竞争力的关键。造成铁路货运时效性差的重要原因之一是运输途中需要在编组站进行有调中转作业。有调中转作业具有消耗时间长且时间波动性大的特点,当一股货流途中需要多次有调中转作业时,其时间消耗及运输时间的不确定性会大大增加,从而导致铁路运输时效性大大降低。
针对上述问题,我国业内专家提出了集装箱班列客车化开行的模式,该模式的基本含义为:货物统一装入集装箱,使用固定平车车底+集装箱运输,列车沿途不解体;中途停站采用侧线停车、利用吊装设备完成集装箱于列车与侧线旁堆场的“乘降”和转移,取消列车中途的解体、调车、编组、货场取送等环节;实现货物运输客运化的组织模式,初期运用于白货物流市场,逐步扩大到无铁路专用线的大宗货运市场[1]。通过初步论证,该模式具有显著的成本优势、时效性优势和物流模式优势,能够创造可观的经济效益。关于集装箱班列客车化开行,相关学者开展了大量理论研究。武兵[2]分析了我国集装箱运输的主要问题,提出了集装箱运输客车化发展的建议并探讨了实施条件和办法。柴甜甜等[3]基于对不同特点集装箱货流所对应开行条件的分析,提出了集装箱班列开行方案优化算法,并以北京—广州为例进行了算例分析。李云涛[4]分析了物流中心之间班列开行的各种影响因素,论述了不同等级集装箱班列的开行条件,并构建了集装箱班列开行方案评价指标体系。文全林[5]分析了铁路集装箱运输各环节的作业流程,建立了网络化条件下的集装箱班列客车化开行方案优化模型。徐利民等[6]针对我国铁路集装箱运输组织现状,研究了三级网络结构下的不同等级节点间集装箱班列开行问题。魏玉光等[7]系统论述了集装箱旅客化快捷运输系统,通过该系统实现集装箱运输旅客化、网络化、班列车底固定化、集装箱设备设施前置化、集装箱运输时间快捷化、集装箱托运客票化、货物运输物流化。夏阳等[8]以快速集装箱列车为研究对象,借鉴旅客列车开行方案的编制方法,结合货物运输的特点,考虑箱流守恒、箱流中转及箱流运到期限等约束,建立新型集装箱系统开行方案的整数线性规划模型,并设计自适应大邻域搜索求解算法。郑平标等[9]从打造货物班列产品体系、构建专业化载运装卸设备体系、强化班列产品运输组织、创新班列产品经营管理模式等方面提出铁路货物班列规模化发展对策。李文晖等[10]设计了涵盖基础层、作业层、感知层、传输层、分析层和决策层的智慧箱管总体架构,提高了铁路集装箱作业的自动化、智能化程度。于剑[11]系统阐述了我国铁路集装箱多式联运在运输价格、运输时效、服务便捷性等方面存在的问题,提出提升运输时效、改进运输服务质量、完善多式联运市场环境等对策建议。
上述研究成果对集装箱班列客车化开行的理论研究起到了积极的推动作用。总体而言,目前既有的集装箱班列客车化开行方案优化模型大多聚焦于列车的开行、停站方案优化,对箱位预分方案鲜有涉及。对于有中间停站的集装箱班列而言,停站方案和箱位预分方案的优劣都是影响列车收益的重要因素。如果站站都停必然会影响列车的时效性,降低运输产品吸引力,所以需要设计合理的停站方案使列车在尽可能多地满足沿线运输需求的同时保证时效性。沿线站点箱位分配原则是在列车装载能力基础上,根据货物运距长短,优先满足长途货流,不合理的箱位分配可能会使短途箱流占用列车箱位,长途箱流的运输需求得不到满足,导致列车运输能力的浪费,降低列车收益。因此,在明确列车的始发终到站后,对停站方案和箱位预分进行合理优化是保证列车收益的重要工作。由于箱位的预分和列车停站方案是紧密联系的,因而将两者纳入同一个模型进行综合优化更有利于寻找全局的最优解。本次研究将针对列车起讫点确定的情况,优先满足长途流,放弃部分短途流需求,满足铁路收益最大化目标。同时为保证列车时效性,设计了停站次数约束,将停站次数限制在一定合理范围内,构建了数学模型,对列车沿途的停站方案和各站的箱位预分方案进行综合优化,并通过算例验证模型的有效性。
2 模型构建
为方便模型的构建,本节引入虚拟弧作为辅助手段构造广义服务路网,假定某列集装箱班列从S1站始发开往Sn站,中途经过S2,S3,…,Sn-1共计n-2个备选停站,针对该情形构建广义服务网络。广义服务网络示意图如图1所示。
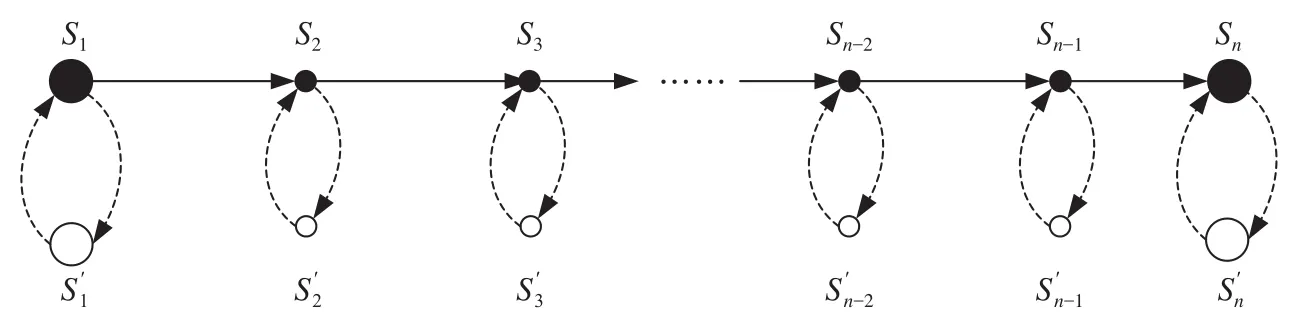
图1 广义服务网络示意图Fig.1 Schematic diagram of generalized service network
在图1中,黑色实线和黑色实心点表示实际的线路和节点,即物理弧和物理节点,黑色虚线和空心点表示虚拟节点和虚拟弧。虚拟弧可以被理解为集装箱的装卸过程,而物理弧则表示集装箱的运输过程。例如在物理网络上由S2运至Sn的运输过程,在广义服务网络上则为从的运输过程,其完整的运输径路为构建模型时将主要通过对虚拟弧的处理实现对停站方案的优化。以S2节点为例,当列车不经停该点时,通过在模型中向弧S2)和加载惩罚项的形式表示该弧处于“断开”的状态,则始发的货物无法发运;当列车经停S2时,通过在模型中向 虚 拟 弧赋予表示实际意义的权重(例如费用)表示该弧处于“连通”状态,则始发的货物可以发运,具体可以发运的数量(即分配的箱位数量)则需要从铁路收益最大化的角度出发,通过模型计算得出。
根据上述建模思路,定义模型所需的各类集合、参数、函数和决策变量,模型符号定义如表1所示。
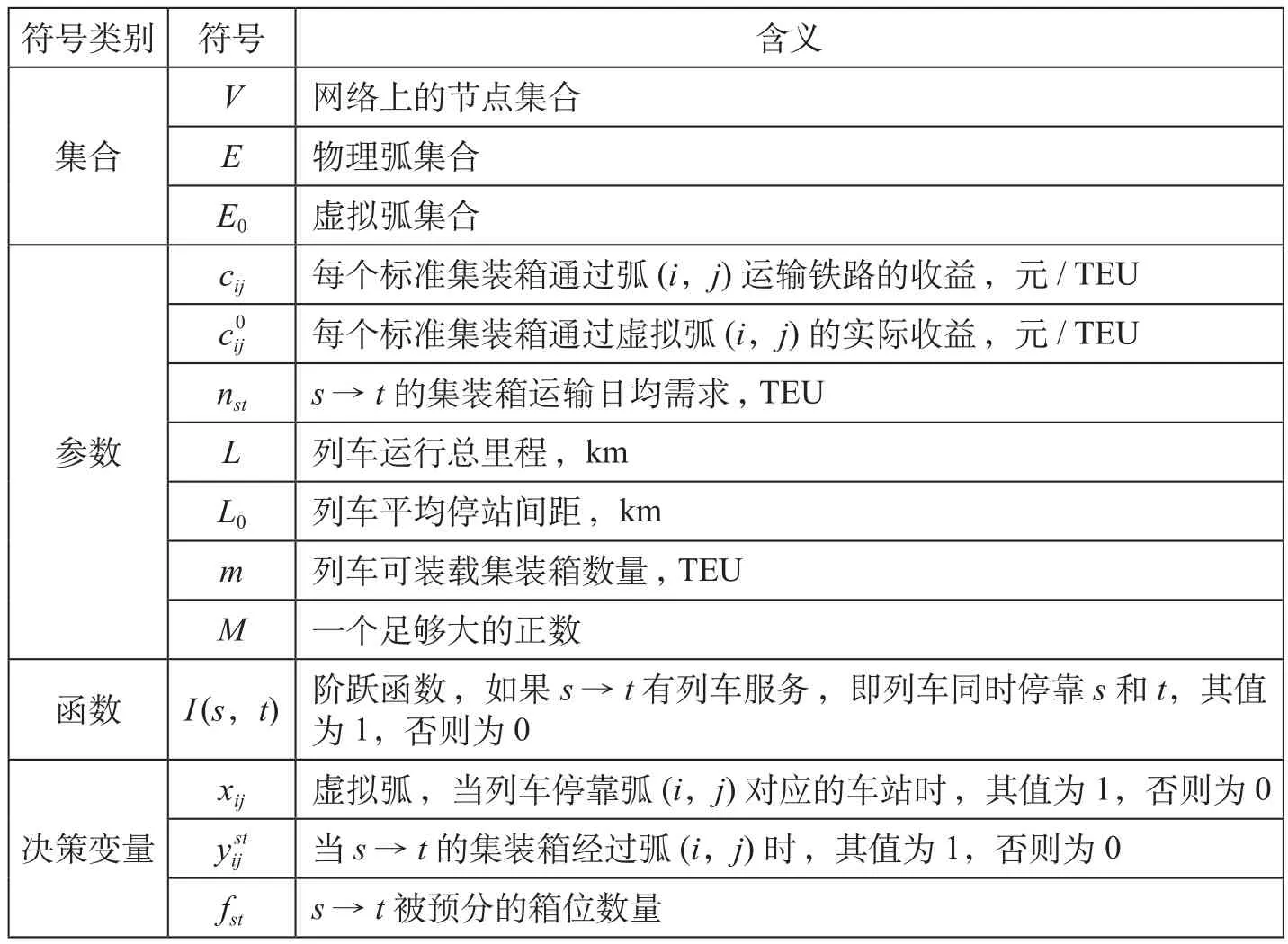
表1 模型符号定义Tab.1 Definitions of model symbols
根据上述参数定义,分步骤构建模型。
2.1 目标函数
模型以列车开行的总收益Z最大化为目标⑴构建函数。
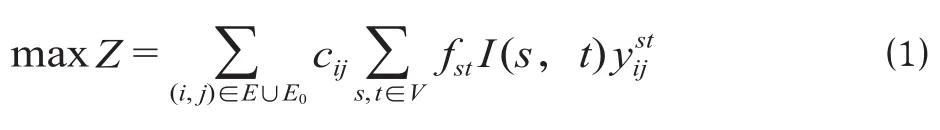
2.2 虚拟弧对称性约束
由于虚拟弧表示集装箱的装卸过程,均为成对的形式出现,因此每一对虚拟弧对应的决策变量取值均应相等。
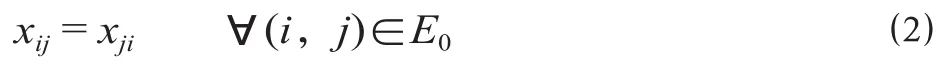
2.3 虚拟弧惩罚约束
针对所有虚拟弧,当虚拟弧对应的车站有列车经停时,相应的xij=xji= 1,此时相应虚拟弧的权重为其实际收益,当虚拟弧所对应车站没有列车经停时,相应的xij=xji= 0,此时相应的虚拟弧的权重包含惩罚项M,为后续约束条件构造提供基础。

2.4 停站次数约束
为保证货物运输的时效性,列车中途停站次数应有一定限制,故根据列车运行总里程以及适宜的平均站间距构造停站次数约束。

2.5 流量守恒约束
为保证各OD间运输径路的完整性,需构造以下约束保证各OD间集装箱运输所经由节点的流量守恒。
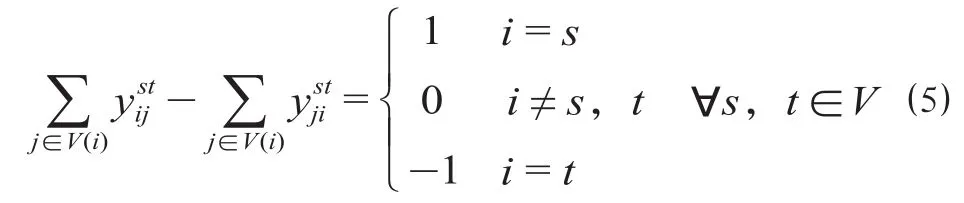
2.6 规避环形径路约束
由于模型以效益最大化为目标函数,而网络中的虚拟弧呈现闭环模式,为防止求解过程中出现虚拟弧重复取值为1的情况,设置以下约束条件使特定车站对应的虚拟弧至多有1个可以取值为1。
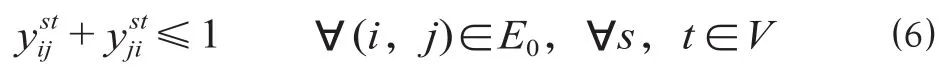
2.7 能力约束
由于列车装载集装箱数量有限,因此设置能力约束使列车在各个区段装载集装箱数量均在能力范围内。
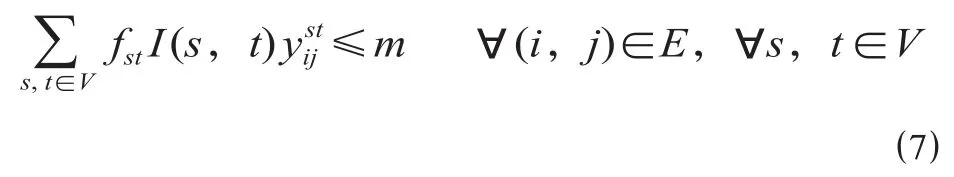
2.8 预分箱位数量约束
构造如下约束条件表示s→t预分的箱位数量应不大于总运输需求量。

2.9 变量取值范围约束
根据参数定义,fst的取值应为自然数,xij和均为0-1变量,用数学形式表达如以下各式所示。

从上述构造过程中可以看出,目标函数以及能力约束表达式中均存在非线性项因此该模型是非线性混合整数规划模型。该类模型采用商业求解器很难在可接受的时间范围内获得满意解。另外,针对该类模型在设计高性能优化算法时也有一定的局限性。因此,需要采用线性化方法将模型转化为线性规划模型,使模型可以被商业软件以较快的速度求解,同时也为开发高性能算法创造便利条件。
3 模型线性化处理
3.1 I (s,t)的线性化处理
引入辅助决策变量zst(zst∈ {0,1})和K,其中K为一有限大的正数,K<M,构造如下辅助约束条件。
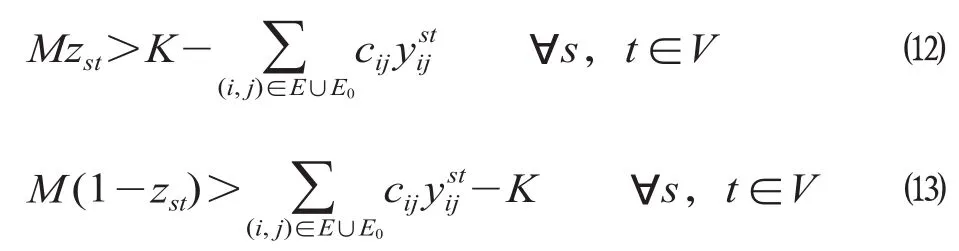
上述约束条件含义如下:当s→t的运输径路经过了有列车服务车站所对应的虚拟弧,即其经过的虚拟弧不包含惩罚项M,那么对于该运输需求那么公式 ⑿ 可化为Mzst>0,由于zst∈ {0,1},所以zst= 1;当s→t的运输径路经过了无列车服务车站所对应的虚拟弧,即其经过的虚拟弧包含惩罚项M,那么对于该运输需求由于K<M,那么公式⒀可以化为M(1 -zst)>0,由于zst∈ {0,1},因而zst= 0。通过以上分析可以看出,无论是哪种情况,总有I(s,t) =zst。因此,模型中的可等效代换为
第一次代换:引入辅助决策变量αst(αst∈N),构造以下辅助约束条件。

与公式 ⒁ 和公式 ⒂ 同理 ,在公式 ⒃ 和公式 ⒄的作用下,无论何种情况,总有因此,可等效代换为
至此,模型实现完全线性化,线性化后的完整模型如下。
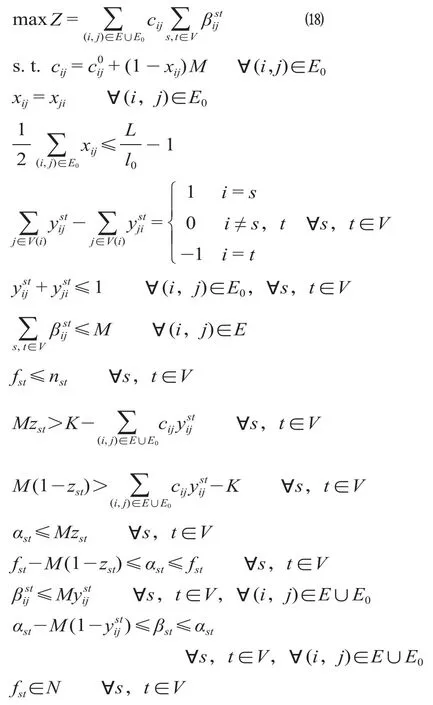
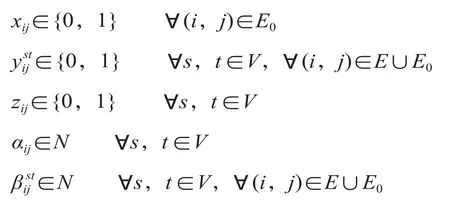
线性化后的模型可以采用高效求解软件求解,同时也有利于编写高性能求解算法。
4 算例分析
本节构造包含9个点的算例进行求解实验以验证模型的有效性,算例示意图如图2所示。
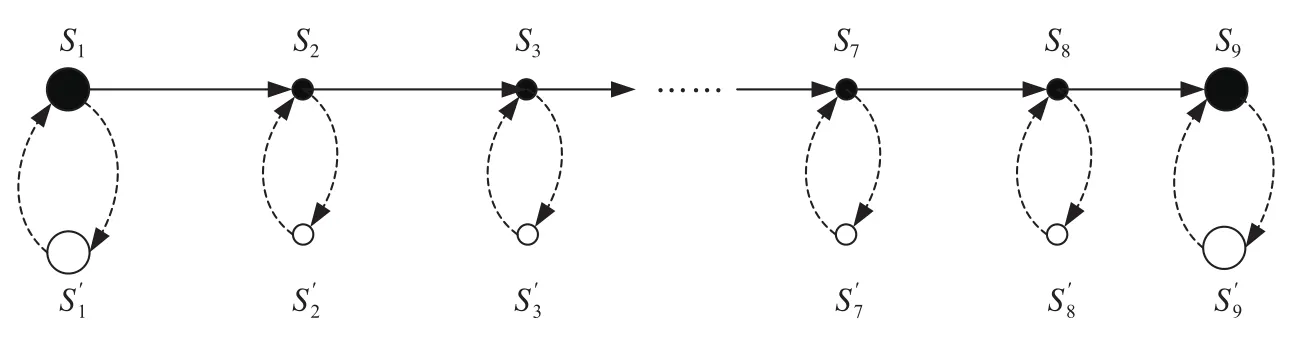
图2 算例示意图Fig.2 Schematic diagram of calculation example
算例输入的运输需求(nst)数据如表2所示。
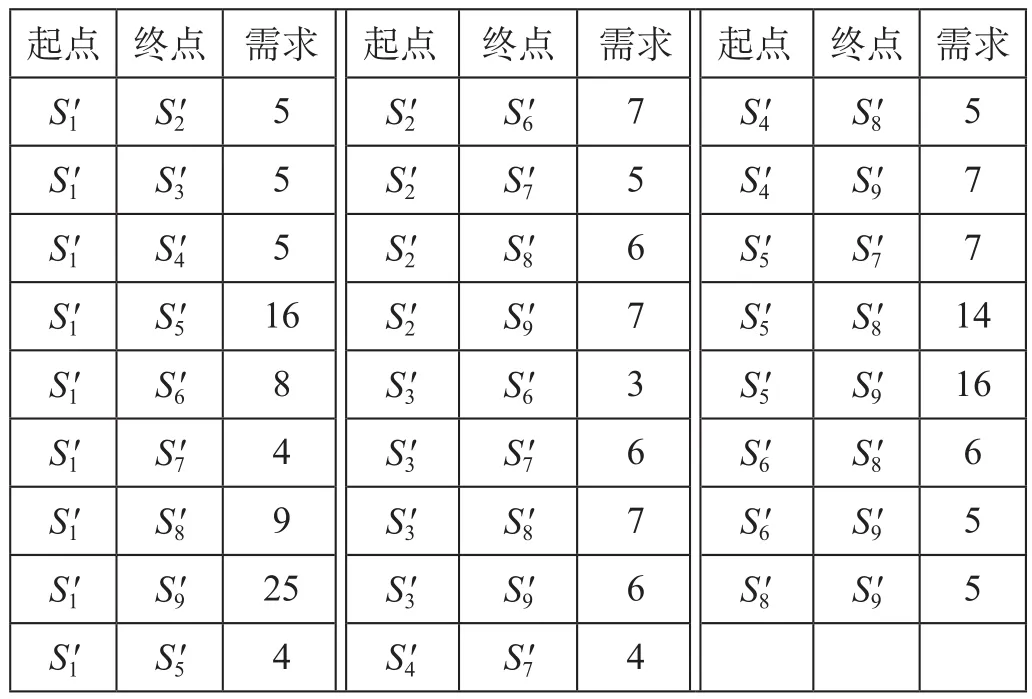
表2 运输需求(nst)数据 TEU/dTab.2 Transportation demand (nst) data
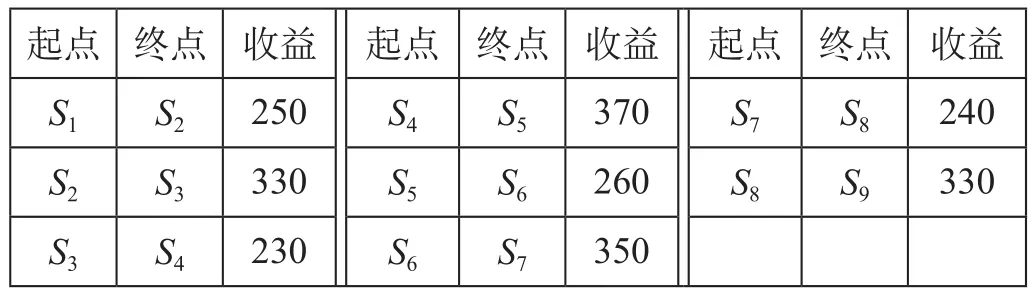
表3 各物理弧单位标准集装箱运输收益(cij) 元/TEUTab.3 Standard container transportation revenue of each physical arc unit
其他参数取值:L= 750;l0= 150;m= 80。
将上述各数据代入模型,运用商业求解软件lingo进行求解,得到求解结果如下。
列车停靠站点:S2,S3,S4,S7,S8。
有列车服务的OD间箱位分配数量如表4所示。
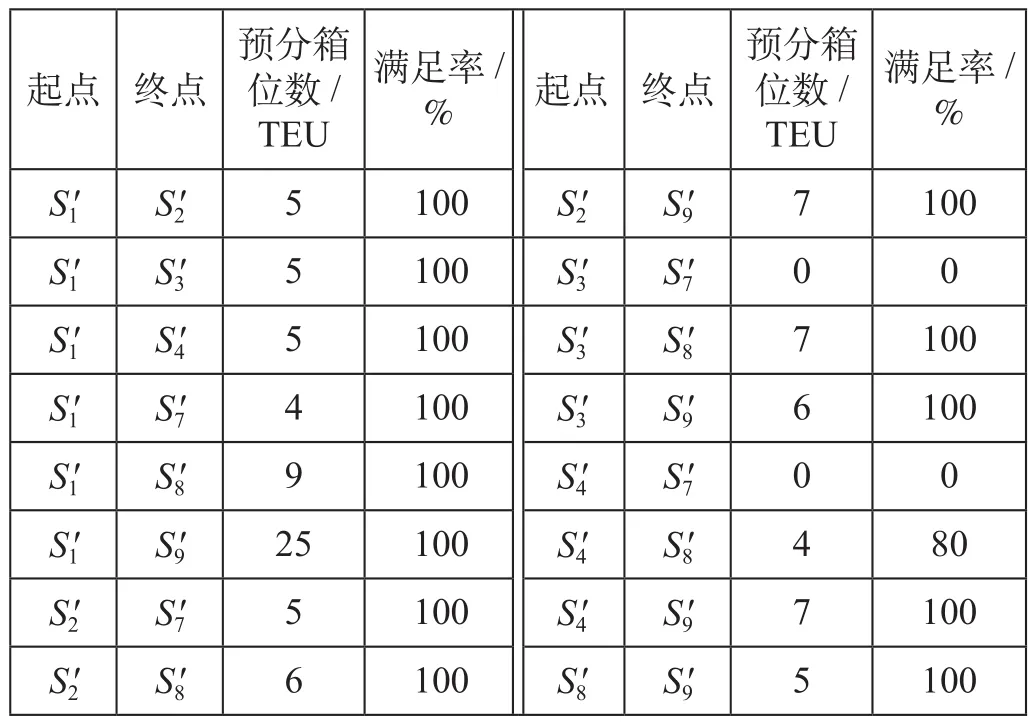
表4 有列车服务的OD间箱位分配数量Tab.4 Allocation quantity in OD space with train service
列车在各区段的集装箱装载情况如表5所示。
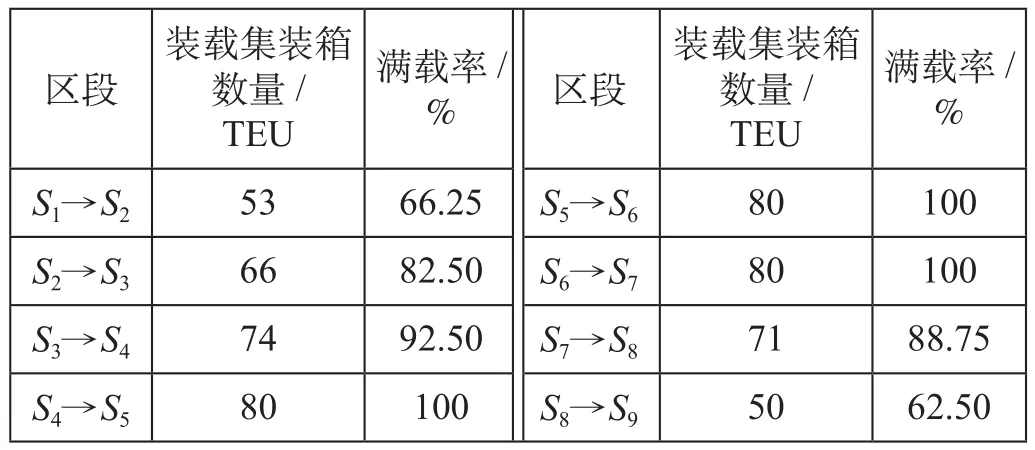
表5 列车在各区段的集装箱装载情况Tab.5 Container loading of train in each section
根据上述结果计算开行单次列车铁路获得的总收益为20.8万元。
通过上述算例分析可知,通过该模型可以求解得出列车停站方案与箱位预分的最优方案,从而使铁路获得最大收益。该算例证明模型是可行有效的。
5 结论
集装箱班列客车化开行作为一种能够显著提高铁路货运时效性的改革思路,已经成为铁路运输组织科研领域的热点问题。研究将列车停站方案和箱位预分方案统筹考虑,通过引入虚拟点和虚拟弧作为辅助,构造了列车停站方案决策变量,进而基于包含虚拟弧和虚拟点的广义路网构建了列车停站方案和箱位预分综合优化模型。针对模型中存在阶跃函数的问题,通过构造辅助决策变量并引入有差异的惩罚项,利用辅助约束条件将阶跃函数转化为非线性多项式的形式,通过2次代换以及辅助约束条件的引入将非线性多项式转换为线性表达式,从而提高模型求解的可操作性。该模型可以使列车在尽可能满足运输需求的同时达到最高的满载率,实现效益最大化。
