基于粒子群优化Stearns-Noechel模型的全光谱木材配色算法研究∗

管雪梅 黄靖一 许宝成 王 荣

（东北林业大学机电工程学院，黑龙江 哈尔滨 150040）

计算机技术的应用推进了木材染色配方预测技术的发展。采用贝叶斯正规化算法和LM（Levenberg-Marquardt）算法相结合的方法对传统BP神经网络进行改进，利用优化后的模型对染色配方进行预测，其仿真结果在精度和网络的泛化方面都有较大的提高[1-3]，但网络收敛速度并没有得到显著改善，且存在训练样本较大的缺点。利用改进的径向基神经网络对染色配方进行预测，其泛化能力在一定程度上有了较大的提升[4]。利用群体智能中的进化算法改进神经网络在建模过程中出现的各类问题，解决了传统BP神经网络在学习训练中存在的局部极值的问题[5-7]。基于此方法的染色配方预测模型可以进一步提高配方的预测精度与模型的收敛速度。基于Friele模型设定固定的参数，然后利用不同的方法预测拟合反射率与反射配方，可以得到色差较小的配色结果，且获得配方的速度较快[8-9]。使用Stearns-Noechel算法建立染色配方预测模型，并对模型参数进行调整，可使配色的预测更加精确[10-12]，大大降低了配色色差，配色效果更佳。将全光谱配色法与Stearns-Noechel模型结合，可以进一步提高配色的精确度与效率[13-15]。

目前，在木材染色配色过程中仍存在效率低、精度差、重复性差、调色的准确性低等突出问题[16-18]。针对这类问题，本研究拟采用粒子群算法（PSO）对Stearns-Noechel模型进行优化[19-22]，以解决配方的预测效率问题与预测准确性问题。依据试验得出的数据，运用MATLAB对参数进行循环计算，将选取最优的参数作为固定值，再通过计算拟合配方使色差最小且小于1。

1 材料与方法

1.1 材料

选取水曲柳（Fraxinus mandshuricaRupr.）木材为染色基材，加工成尺寸为60 mm×40 mm×0.5 mm（L×W×H）的单板。

染色试剂：活性红染料（X-3B）、活性黄染料（XRG）、活性艳蓝染料，产于天津天顺化工染料有限公司。

其他试剂：染色渗透剂JFC、固色剂（无水碳酸钠Na2CO3）、双氧水溶液、漂白缓冲剂（硅酸钠Na2SiO3）、促染剂（氯化钠NaCl），产于北京化工厂。

1.2 设备

HH-8 型数显恒温水浴锅（上海力辰）、202-1A型电热恒温干燥箱（泰斯特）、高光谱成像仪（SPECIM公司、芬兰）、电子天平（上海花潮）、电子天平，自制染色笼等。

1.3 样品制备

由于木材本身带有颜色，且颜色分布不均，这将对染色效果产生较大的影响。因此，在进行单板染色试验前，需对水曲柳单板进行漂白处理。首先配置浓度为4%的双氧水溶液，然后加入漂白缓冲剂Na2SiO3，用玻璃棒搅拌均匀。将染色基材（水曲柳单板）放入自制的染色笼中并放入烧杯，然后倒入漂白液，设置浴比为1∶20，65 ℃条件下水浴处理2 h。漂白结束后，用清水冲去单板表面的残液，然后将单板置于65 ℃的干燥箱中进行干燥，使其含水率降至8%。

漂白结束后，将浓度为1%的活性染料、渗透剂JFC和促染溶剂NaCl混合配置染色溶液，将漂白后的单板放入染色笼中并放入烧杯，向烧杯中加入染色液，设置浴比为1∶20。将烧杯放入恒温水浴锅中，染色2 h后再加入固色剂Na2CO3固色30 min。固色结束后，取出染色单板并采用清水冲去表面残液，再将单板放入65 ℃的干燥箱中干燥至含水率为8%。

漂白后的水曲柳单板与染色单板的表面照片如图1所示。

图1 水曲柳漂白单板及单一组分染料染色材效果图Fig.1 Effect diagram of ash bleached veneer and single component dyestuff dyeing material

2 基于Stearns-Noechel算法的光谱配色模型

根据Duntley理论，将单色样按照不同比例进行混合后得到的混色样其光谱反射率可由单色样的反射率与混合比例的乘积的加和表示。在此基础上，Stearns与Noechel[23]通过大量试验推导出了一个关于反射率的函数式，即Stearns-Noechel模型。

2.1 光谱配色算法

运用高光谱成像仪对混合染色样品表面进行扫描获取其表面光谱反射率，即标准样的反射率，记做Rs（λ） 。成立，其中当波长为λm时，计算样的反射率由Rs（λ）表示。

偏差用最小二乘法求极小值。根据色谱测色范围取（400～700 nm），波长间隔20 nm，根据公式：

因为Δ趋于极小，对浓度比例的偏导数均为0。所以下式成立，即可得到不同颜色的单色染料的浓度比例A。

2.2 Stearns-Noechel模型参数M的确定

Stearns-Noechel模型的核心环节就是对算法中M值和各组染料初始配方的确定。

经过大量试验，Stearns和Noechel在Duntley理论的基础上提出一个经验公式[24-25]，即Stearns-Noechel模型：

通过式（7）可发现首先要处理的问题是确定公式中未知参数M值。

求解未知参数M值具体思路为：测色得到的混合染料的反射率，利用MATLAB对参数M循环赋值，拟合光谱反射率，结合光谱反射率求色差最小时M的最优值。具体求解过程图如下图2 所示。

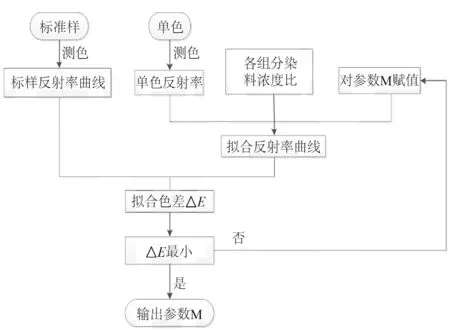
图2 最佳参数M值计算方法Fig.2 The best parameter M value calculation method

本试验根据选取的10 组不同浓度比例的三色混合染料，计算最优参数M值，即M=0.48。

3 基于粒子群优化修正算法模型

3.1 适应度函数

粒子群优化算法是一种智能算法，其原理是模仿鸟群或者鱼群在群体中找到适合自己位置的最优点，适应度是其算法的评价因子，其中每个粒子都有其相对应的适应度[26]，考虑到这点适合于光谱反射曲线的拟合，因此选用此算法进行优化修正，适应度函数如下：

3.2 粒子群优化算法模型

为使最后得到的试验配方更加精确，本研究对原模型进行修正改进，具体试验流程如图3 所示。

如图3 所示，基于Stearns-Noechel模型的光谱配色算法对拟合反射率曲线进行修正计算，获得染色配方即各单色染料浓度比和拟合色差值。其中

图3 优化算法模型Fig.3 Optimization algorithm model

4 试验分析

4.1 计算偏差

为得到更精确的配比，本次研究采用配方的相对偏差计算公式对偏差进行计算。

4.2 计算色差

利用MATLAB分别对10 组试验式样进行拟合样配比计算，得到的结果如表1 所示。

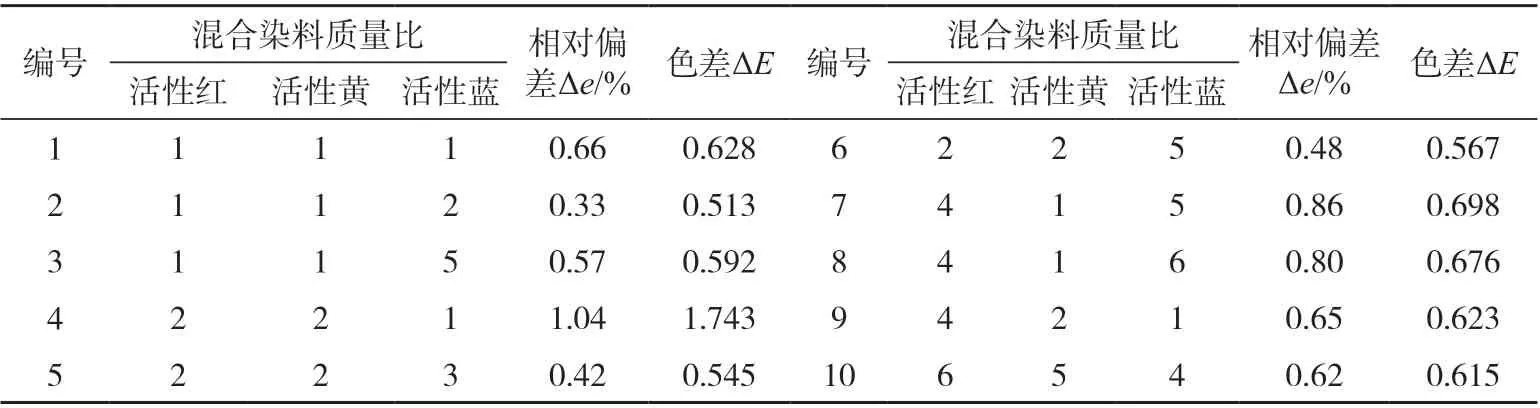
表1 混合染料质量比Tab.1 Mass ratio of mixed dyes

素板（未处理）和染色单板的反射率结果如表2所示。选用紫檀、黑酸枝、黑胡桃和柚木木材用作标准样本，用高光谱成像仪测量这些木材表面的反射率，结果如表3 所示。

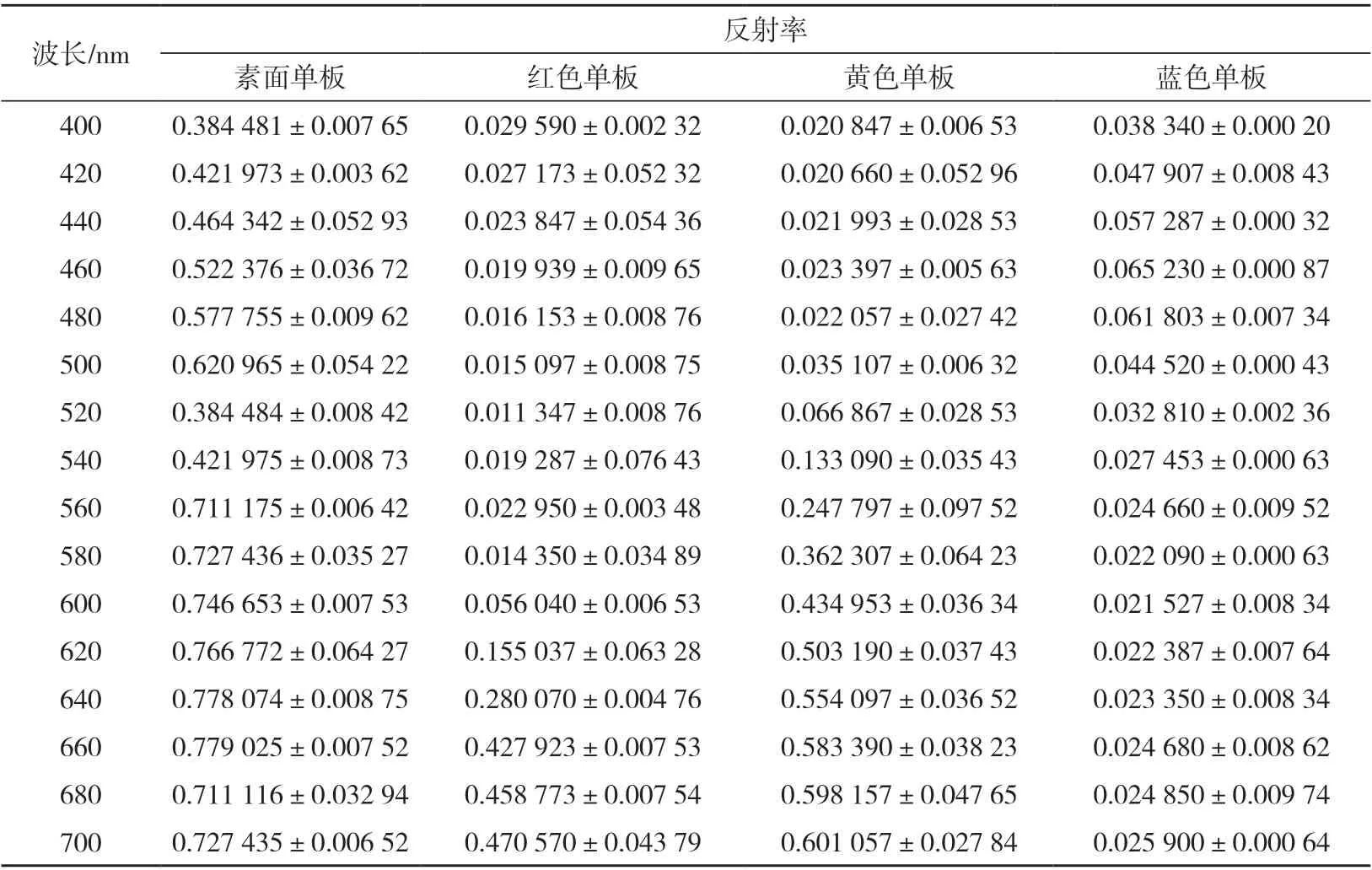
表2 染色材表面反射率测定结果Tab.2 Results of surface reflectance measurement of dyed materials

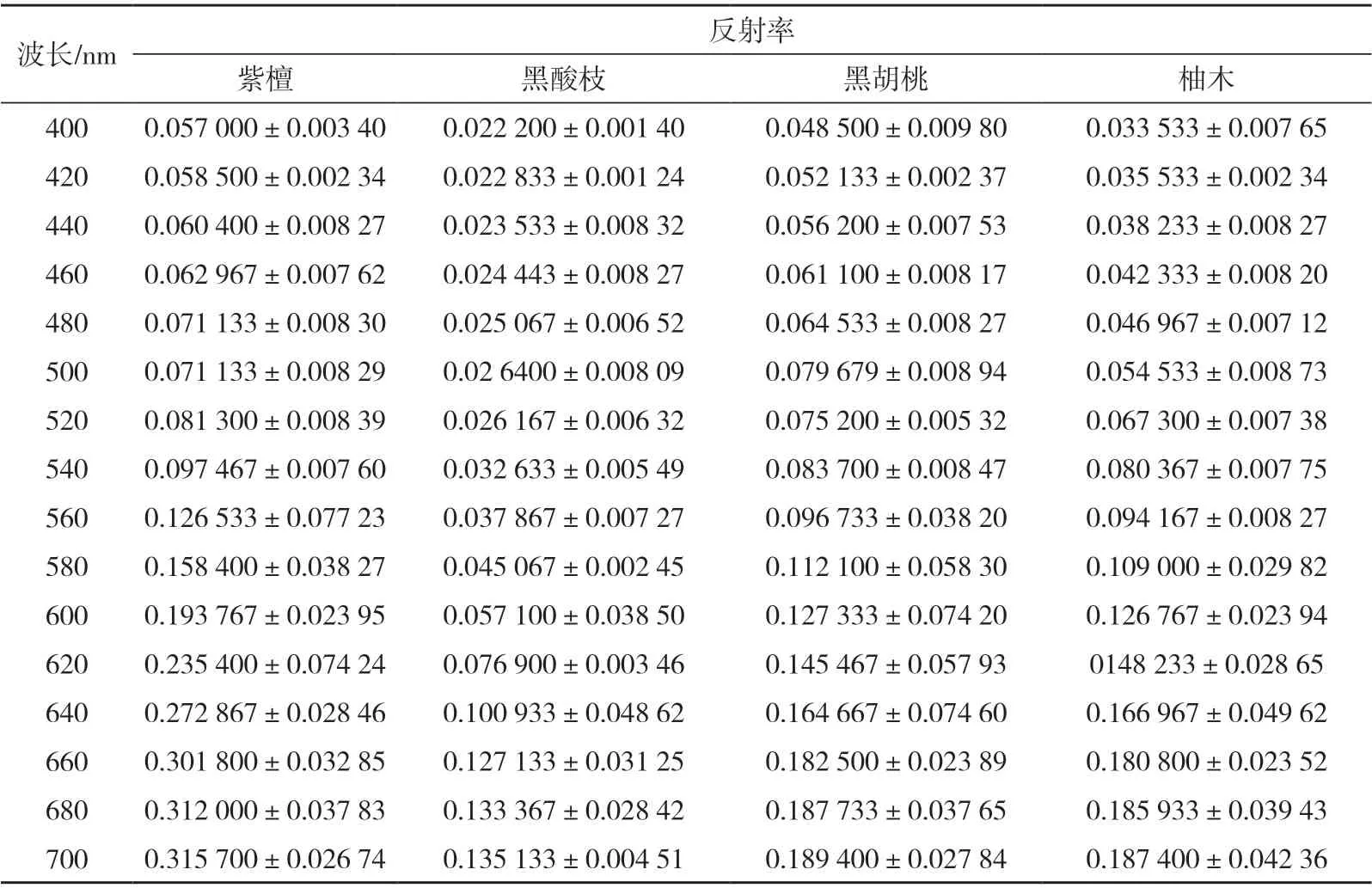
表3 珍贵树种表面反射率测定结果Tab.3 Reflectance of precious tree species

利用MATLAB对数据处理，获取拟合反射率曲线误差对比如图4 所示。

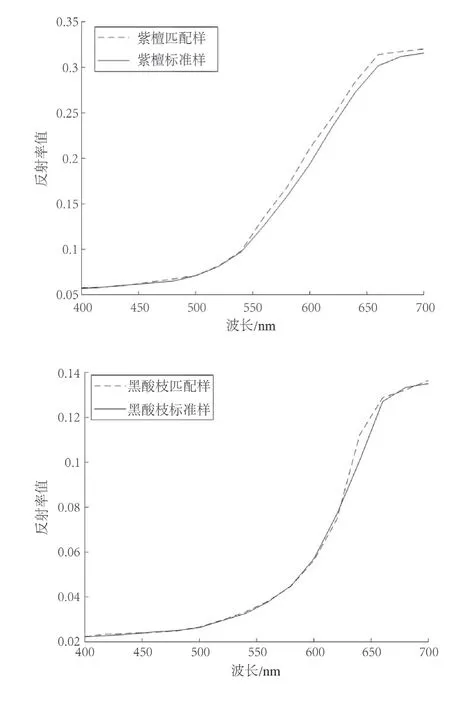
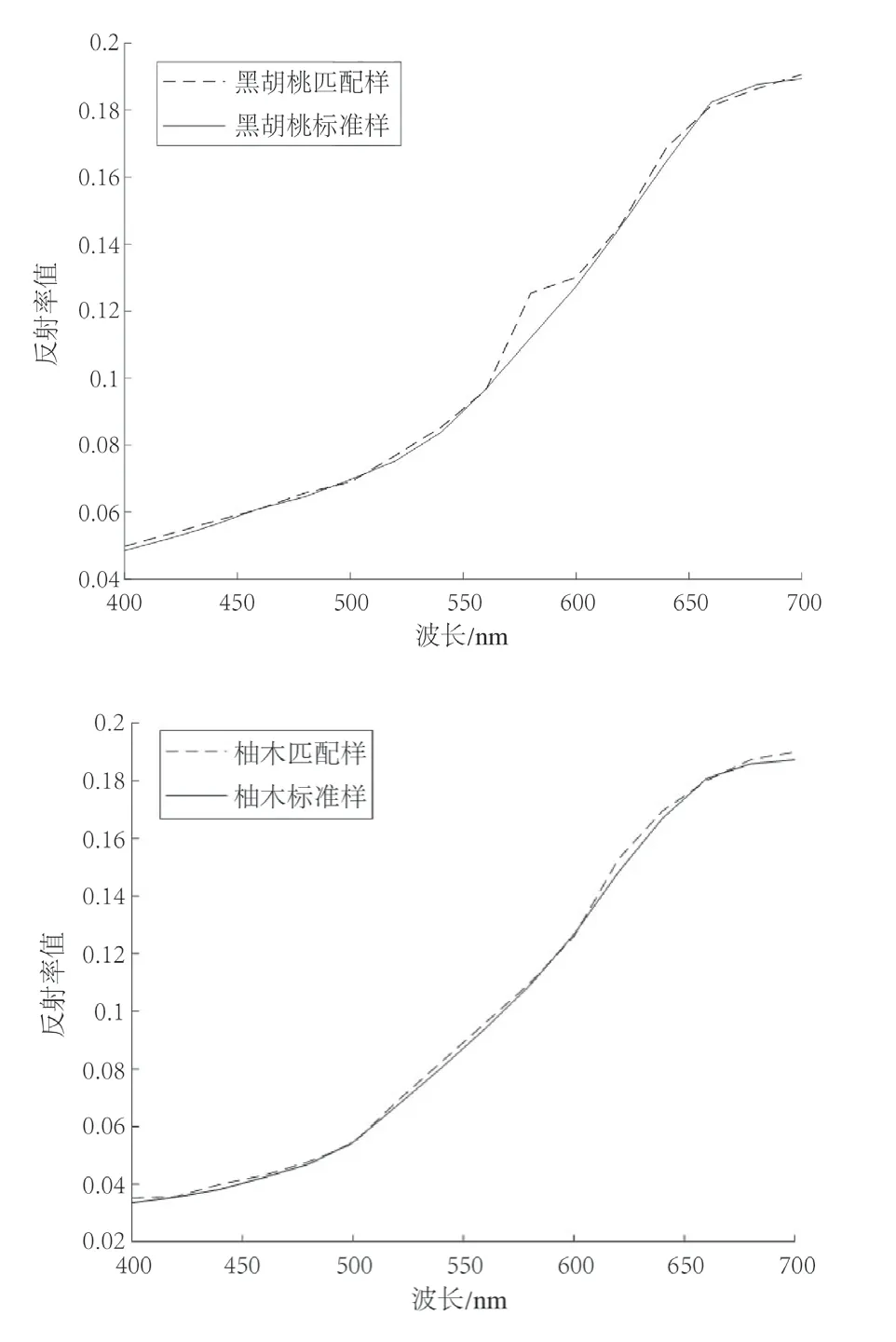
图4 珍贵树种拟合反射率误差对比图Fig. 4 comparison diagram of fitting reflectivity error of precious tree species

从反射率曲线图和表1、2 数据可以看出，本研究所用的改进模型能有效提高原来模型配色效率和配色准确度。从相对偏差来看，平均相对偏差0.643%，最大相对偏差1.04%，最小相对偏差0.33%，符合误差范围。从色差结果来看，平均色差0.720，色差结果理想，说明模型改进后对染色配色效果有较大提高。天然木材标样点如图5 所示，本研究所用算法的染色效果如图6 所示。

图5 天然木材标样点Fig. 5 Natural wood sample point

图6 算法染色效果图Fig. 6 The algorithm dyeing effect diagram

5 结论

本研究采用粒子群算法对Stearns-Noechel模型进行了优化，并利用优化后的模型对珍贵材的配方进行了预测。采用了MATLAB对模型中的固定参数M进行循环计算，采用色差最小时的固定参数M值作为最优参数对染色木材的配方进行预测。结果表明，预测配方的平均相对偏差为0.643%，平均拟合色差为0.720，配色效果有一定提升，接近真实配方。改进的算法模型能够提高染色效率和准确率，为木材染色技术提供借鉴。