移动荷载下梁索组合结构瞬态响应分析

纪键铱，王荣辉，马牛静，余贤宾，陈 木

(华南理工大学 土木与交通学院，广东 广州 510640)

在桥梁结构设计中，往往通过桥梁杆件的静力影响线计算车辆荷载下的杆件内力。通过动力系数反映荷载的冲击作用；而冲击系数取值的合理性、影响线分析时边界模拟的可靠性，特别是针对斜拉桥等大跨径桥梁在车辆荷载下的实际响应，一直有很多讨论。针对各类桥梁，有学者建立车桥耦合振动系统，采用模态叠加法或逐步积分法等传统结构动力学求解方法，分析桥梁结构的动力学响应，研究桥梁冲击系数与振动加速度等动态指标的变化规律。卢海林等采用newmark-β法求解车辆荷载下大跨径弯桥的振动响应，发现考虑单一冲击系数会造成设计值的过盈或者不足。以上方法多应用于连续梁桥的动态响应评估，对于复杂结构体系桥梁或大跨径斜拉桥结构，多采用有限元法进行分析求解。肖烨和罗小勇针对列车提载对既有桥梁的影响，建立列车-轨道-桥梁耦合有限元模型，分析列车提载对现有桥梁动力响应的影响规律。以上研究能够得到桥梁结构在移动荷载下的整体响应特性，但难以从机理上解释动态行为的变化规律。结构的动态响应可以看作是波的传播和叠加，特别是对于大跨度梁索组合体系的桥梁而言，扰动在结构中的传递过程不可忽略。因此，若采用波动理论来求解梁索组合结构的冲击响应问题，不仅可以使得结果具有明确的物理概念，也便于研究者从应力波传递机理的角度为结构设计优化提供建议。本文采用的回传路径矩阵法（MRRM）是一种求解弹性波传递函数的矩阵分析方法。

Pestel和Leckie总结了连续系统中传递矩阵法（MTM）的基本原理和修正方法，并讨论了MTM如何应用于各种工程问题。该方法一经提出，便不断有学者对其进行改进补充。在MTM的基础上，Howard和Pao提出传统回传路径矩阵法（MRRM），分析冲击荷载下，弹性波在平面桁架内的传播过程。MRRM作为一种频域矩阵分析方法，由于使用了Neumann级数展开技术，避免了大多数频域矩阵方法都存在的矩阵元在结构的共振频率处会表现出奇异性的缺点。相较于有限元法，MRRM求解结果是基于行波解，避免了离散误差；与常用的结构动力学中求解振动微分方程的时域逐步积分法相比，又避免了收敛的问题。

MRRM提出后，有学者利用该方法精确有效地预测无限层状介质、层合梁、框架和圆柱形板壳结构的短时瞬态响应和动态性能。陈进浩、许兰兰等运用MRRM对框架结构在冲击荷载下的短时瞬态响应进行一系列的研究，分析不同传递路径弹性波传播时差及波形特征，并基于该方法进一步讨论框架结构的自振特性。Li和Nie引入MRRM，对具有内加劲肋的多跨矩形薄板进行屈曲分析，推导了回传路径矩阵的计算算法，用以确定屈曲载荷。一系列的研究成果都说明了MRRM法在求解结构动态响应方面的可靠性和广泛的适用性。然而，由于采用的Neumann级数展开技术对于求逆的矩阵有苛刻的要求，传统MRRM法多应用于求解非弥散的纵向弹性波或者结构的短时瞬态响应，例如，Jiang等采用了Neumann级数展开技术，展开级数的数量受到限制，仅能预测结构的早期响应；且由于对求逆矩阵的诸多要求，在此之后的相关研究也多将研究对象限定为简支和连续梁。

针对上述研究的不足，本文基于DFT思想，推导结构波动响应的级数解，进而避免了矩阵元在求逆过程中的奇异性问题，且通过试验和有限元对改进后的算法进行验证。在此基础上，将MRRM应用于移动荷载作用下梁索组合结构的瞬态响应求解及频谱分析。同时，从理论结果出发，讨论所选取的截止频域对MRRM法计算精度及计算效率的影响，进一步提高MRRM的计算效率。

1 梁-索结构模型理论分析

1.1 斜拉结构力学模型

梁-索组合结构如图1所示。由图1可见：支座和梁索连接位置作为节点，以I、J、O、K、L、M进行编号；单元以两端节点编号进行命名，IJ、JO、OK、KL为铁木辛柯梁单元，在节点J、K处以角度 α与索单元MJ、MK相连；移动集中力

P

以恒定速度

V

，从节点I向L运动。对于任一单元，在其两端节点分别建立一个单元局部坐标系，以节点为坐标系原点，

x

轴平行于单元，其正方向指向单元另一节点；

y

轴垂直于单元。以图1（b）中单元IJ为例，引入双局部坐标系统，即在I、J节点分别建立局部坐标系，I节点处坐标系用

x

和

y

表示，J节点处轴坐标为

x

和

y

。梁单元平衡方程采用铁木辛柯梁理论，对于斜拉桥结构而言，移动荷载造成的索的弹性振荡压应变远小于桥梁自重荷载及索张拉力引起的弹性拉应变，所以在索单元中采用1维弹性杆理论来模拟移动荷载引起的斜拉索中弹性波的传递是合适的。

图1 梁-索组合结构模型Fig. 1 Model of beam-cable structure

以IJ梁单元和JM索单元为例，局部坐标系下的铁木辛柯梁波动方程（1）和（2）和1维杆单元波动方程（3）如下：

式（1）～（3）中：

c

为 索中纵波波速，

c

=

E

为索单元弹性模量， ρ为 索单元密度；

y

为梁单元横向位移；

φ

为梁单元截面转角，

u

为索单元轴向位移，梁单元与索单元为等截面单元，材料特性不变； µ为与截面形状有关的数值因子；

A

为梁单元面积；

G

为剪切模量；

E

为弹性模量；

I

为截面惯性矩； ρ为梁单元密度；

q

为梁上作用的横向分布荷载。

节点处的单元位移协调与内力连续：

I节点：

y

(0,

t

)=0，

M

(0,

t

)=0；J节点：

y

(0,

t

)=−

y

(0,

t

)，

φ

(0,

t

)=

φ

(0,

t

)，

y

(0,

t

)=−

u

(0,

t

)sin α，

M

(0,

t

)+

M

(0,

t

)=0， sin α

N

(0,

t

)=

V

(0,

t

)−

V

(0,

t

)；O节点：

y

(0,

t

)=0

，

y

(0,

t

)=0

，

φ

(0,

t

)=

φ

(0,

t

)，

M

(0,

t

)+

M

(0,

t

)=0；K节点：

y

(0,

t

)=−

y

(0,

t

)

，

y

(0,

t

)=−

u

(0,

t

)·sin α

，

φ

(0,

t

)=

φ

(0,

t

)

，

M

(0,

t

)+

M

(0,

t

)=0，sin α·

N

(0,

t

)=

V

(0,

t

)−

V

(0,

t

)；L节点：

y

(0,

t

)=0

，

M

(0,

t

)=0；M节点：

u

(0,

t

)=0，

u

(0,

t

)=0。其中，

N

为轴力，

V

为剪力，

M

为弯矩。

1.2 控制方程数值求解

常系数非齐次偏微分方程如式（1）、（2）和（3）所示，其通解是对应的齐次方程通解和非齐次方程本身一个特解之和。齐次方程通解形式可以表示为完整解，如式（4）、（5）和（6）所示：

将式（4）、（5）和（6）代入波动方程（1）、（2）和（3）的齐次方程，对于非齐次方程的特解采用拉普拉斯变换解法，最终得到控制方程的通解式（7）、（8）和（9）：

式中：待定系数

a

、

a

、

a

、

K

a

和

K

a

分别为节点

i

各入射波分量波幅；

d

、

d

、

d

、

K

d

和

K

d

分别为节点各出射波分量波幅；

k

、

k

、

k

分别为铁木辛柯梁频散关系，在吴斌、Doyle等的研究中均有描述，这里不再赘述；

P

和

P

为引入的外荷载影响量，为波动方程特解。若荷载大小不变，恒为

q

，移动荷载

q

(

x

,

t

) 可采用狄拉克函数 δ及跃阶函数

H

表示，这里仍以单元IJ来说明，如式（10）和（11）所示：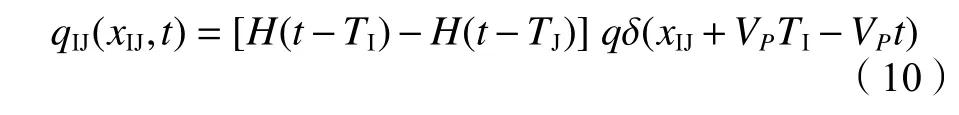

波动方程特解表达式如式（12）和（13）所示：

1.3 回传路径矩阵法的基本原理

根据局部坐标下节点处的位移协调和内力平衡关系，建立节点处的应力波散射关系：

式中，

d

为节点I出射波波幅向量集合，

a

为节点I入射波波幅向量矩阵，

S

为节点I局部散射矩阵。

所有局部散射矩阵组合成结构整体散射矩阵：

引入图1同一单元两端节点的位移协调关系，建立结构中波幅向量之间的相位转换关系如式（16）所示：

式中：

P

为相位转换矩阵，其中，

L

为单元长度；

Q

为激励源向量。将单元相位转换矩阵组合为整体矩阵，得到

a

=

P

+

Q

， 其中，

P

为整体相位转换矩阵，与出射波矩阵

d

元素位置顺序不同。引入置换矩阵

U

，调整出射波向量

d

中元素位置，得到：

联立式（15）和（17）得到：

式（18）～（19）中：

R

为回传路径矩阵，

R

=

SPU

；

s

为波源矢量，

s

=

SQ

。将式（18）和（19）代入式（7）、（8）和（9），即可得移动荷载下结构的瞬态响应。当结构发生自由振动时，(

I

−

R

)

d

=0，此时系数行列式：

1.4 基于离散傅里叶变换的级数展开

(

I

−

R

)

由于自振频率的存在， 有无穷多个极点，该矩阵无法直接求逆。Howard和Pao提出利用Neumann级数展开法近似求解，随后的研究者也多采用该方法。然而，该方法的适用条件十分苛刻，要求回传路径矩阵满足：

该方法仅适用于求解非弥散的纵波及横波的早期瞬时响应。

基于离散傅里叶变换（DFT）的原理，如式（7）、（8）和（9）可写为级数展开形式，如式（22）、（23）和（24）所示：

式中，

t

为第

k

个时间点。在此前提下，对于取值满足DFT的任一 ω，ω=2π

nF

/

N

（0 ≤

n

≤

N

−1，

N

为采样点，

F

为采样频率），求得的(

I

−

R

)内矩阵元素均为确定的数值，故可直接代入 (

I

−

R

)，求得广义逆矩阵，进而通过式（18）和（19）计算得到离散傅里叶系数，由逆FFT求解或通过级数展开式（22）、（23）和（24），得到结构的瞬态响应。

2 理论方法正确性验证

通过简支钢箱梁实桥动力测试，获取跑车时的箱梁底部动应变变化规律；结合有限元分析结果，对改进后的MRRM法在梁单元中的应用进行验证。试验现场布置和试验桥梁结构如图2和3所示。其中，动态应变测点（图2（c））布设在跨中钢箱梁底部中线处（图3（a）），通过连接着信号放大装置的动态应变测试系统DH8003（图2（e）、（f））读取实时应变，采集频率为2 000 Hz。

图2 试验现场布置Fig. 2 Diagram of field test device

图3 试验桥梁结构Fig. 3 Structure of test bridge

图3中，试验桥梁为单箱简支钢箱梁桥，桥梁跨度为22.5 m。该桥为新建桥梁，桥面为平顺的沥青铺装层，在桥上以速度30和40 km/h，从左至右行驶一总重19.8 t的两轴试验车辆，严格控制加载过程中车速恒定且沿车道中心直线行驶，避免车辆由于车头摆动或者加减速带来的影响。该车轴距3.25 m，轴重分配通过磅秤测得，前后轴载分别为

P

=8.1 t和

P

=11.7 t。

使用有限元软件ABAQUS建立两个独立移动点荷载（前后轴载）作用下的简支梁单元模型。梁单元采用B31单元模拟，桥梁结构参数见表1。

表1 试验桥梁参数
Tab. 1 Parameters of the test bridge

密度/(kg·m-1)弹性模量/(105 MPa) 截面积/m2 截面惯性矩/(10-2 m4)7 850 2.06 0.292 6.67

移动荷载采用ABAQUS子程序VDLOAD进行编程调用，定义移动荷载大小、移动速度及作用位置。

本文算法采用的FFT采样频率为1 000 Hz，采样数为16 384，根据铁木辛柯梁几何方程，梁单元底部弯曲应变 ε可由式（25）得到：

式中，

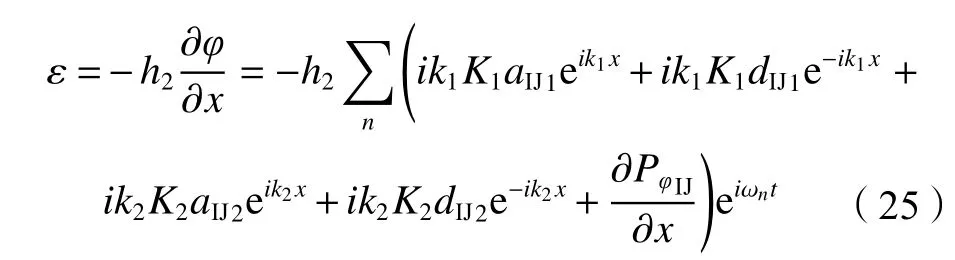
h

为截面形心轴到钢箱梁底面距离。

由本文算法、有限元算法及试验得到的跨中位置钢梁底面弯曲动应变时程曲线对比如图4所示。由于现场加载过程，实际车速不可避免与试验控制车速有所偏差，故实测曲线的波峰和波谷与理论曲线有一定偏移。本文算法结果与现场实测的桥梁跨中动应变波动变化趋势较为接近，应变幅值有一定偏差。

由图4（a）可见：当

V

=30 km/h 时，实测曲线的波动趋势与理论曲线能较好吻合。当车辆逐渐接近跨中位置，实测曲线在个别点处出现实测波峰不明显的情况；当

t

=1.2 s时，此时实测应变与理论应变峰值出现最大的偏差为22%，大部分位置处实测曲线的波动趋势与理论曲线仍能较好吻合；当

t

=1.54 s时，即车辆移动到跨中位置，应变幅值出现的偏差为8%。由图4（b）可见：当

V

=40 km/h 时，实测曲线的波动趋势与理论曲线能较好吻合。车辆移动到跨中位置处，当时间

t

=1.2 s时，应变幅值偏差为9.8%；在车辆逐渐接近跨中位置的过程中，实测应变曲线在少数位置出现波峰不明显的现象，当

t

=0.8 s时，应变幅值出现最大偏差26%。造成以上情况的原因是进行实桥试验时，桥面铺装、两侧防撞墙和截面内部的纵向加劲肋均会增大截面刚度，使实测结果整体略小于理论结果。且在实桥现场测试过程中，干扰因素较多，现场粘贴在箱梁底部的应变片测得的应变数据不可避免会有所损失，这也是局部点位处出现实测峰值不明显，造成应变幅值偏差较大的原因。故该计算结果是合理的，且本文算法结果与实测结果相比，波动趋势基本相符合。

图4 简支梁跨中弯曲动应变时程曲线对比Fig. 4 Comparison of flexural strain at the lower surface of the beam at mid span

本文算法计算得到的动应变曲线和有限元结果较为接近，移动荷载时速

V

=30 km/h，

t

=1.56 s时，应变幅值出现最大偏差，为5%；当

V

=40 km/h，为4%。由此可推知，本文算法在计算移动荷载下桥梁结构的瞬态波动响应具有较高的可靠性。图5为车辆时速为40 km/h，两个轴载分别作用下，跨中处弯曲动应变时程曲线对比，其中，起始时刻

t

=0，是前轴作用简支梁的开始时刻。前后轴作用下，最大动应变比值为18.580 /27.200=0.683，与前后轴载比值0.692接近。移动荷载离开之后，结构以0.133 s的振动周期进行自由振动，振动频率为7.52 Hz。根据式（20）计算得到的结构1阶自振频率为7.53 Hz，说明外加扰动消失后，结构以1阶自振频率进行震荡。以上现象与实测结果和力学常识相吻合，说明本文算法在结构动态响应计算方面的适用性。

图5 试验轴载作用下跨中弯曲动应变时程曲线Fig. 5 Dynamic flexural strain time history curves under experimental axial load of the beam at mid span

3 梁-索组合结构波动响应分析

为研究斜拉桥结构中应力波的传递规律，以图1力学模型为研究对象进行分析，相关结构参数见表2，移动荷载取15 000 N，荷载移动速度取20 m/s，梁索之间的夹角取45°和90°。

表2 梁-索组合结构体系参数
Tab. 2 Parameters of cable-beam structure system

构件 密度/(kg·m-1)剪切模量/(1010 Pa)弹性模量/(1011 Pa)截面积/(10-3 m2)惯性矩/(10-3 m4)主梁 7 850 7.923 2.060 250.000 1.302斜拉索 8 005 — 1.950 7.854 —

3.1 动力时程分析

索梁夹角α为45°和90°时，单元JO跨中位置横向位移曲线如图6所示。由图6可知：本文算法结果的波动趋势与有限元结果具有较高的吻合度，在荷载移动至JO跨中附近时，理论结果曲线变化更为平滑，这是由于有限元结果存在离散误差，且有限元动力分析采用差分法，求解响应易出现震荡。相比有限元结果，本文算法得到的位移峰值较大， α=45时，偏差为9%； α =90时，偏差为8%。这是因为尽管研究对象为无阻尼体系，但是有限元分析中默认以体积黏度的形式引入人工阻尼，故波在有限元分析中是耗散的。分析表明，本文算法的计算结果合理，理论分析正确。由图6可知，随梁索夹角增大，在同样的移动荷载作用下，主梁横向位移减小，即较大的梁索夹角可以增大结构体系的动刚度。

图6 两种算法计算单元JO跨中位移曲线对比Fig. 6 Comparison of displacement curves of JO at mid span calculated by two algorithms

图7为梁索夹角 α =90，索单元JM在M节点位置的轴力变化曲线。用本文算法计算得到的最大轴力为1.559×10N，用有限元动力分析得到的最大轴力为1.651×10N，相对偏差为5%，且曲线波动趋势基本一致。与有限元静力分析结果1.477×10N相比，索力的放大系数分别为0.06和0.11。

图7 斜拉索JM在节点M处轴力（ α=90°）Fig. 7 Axial force of JM at Joint M when α=90°

图8为梁索夹角 α=90，以移动荷载作用总时间为1

T

，在0～8

T

时间内，JO单元跨中位置处的横向位移曲线。由图8可见，移动荷载离开后，结构响应趋于稳定，以固定周期和幅值往复运动，一个完整的振动周期包含7个自振周期，自振周期大致在0.340～0.384 s。表3为本文算法和有限元法计算得到的梁索组合结构前5阶自振频率及两种方法计算结果的偏差值。由表3可知，发现移动荷载离开后，结构以1阶和2阶自振频率循环往复运动。

图8 0～8T 时间内单元JO跨中横向位移曲线Fig. 8 Deflection curves of the JO element at x=0.5L during 0～8T

3.2 频响分析

如表3所示， α=45时，使用本文算法计算得到的梁索组合结构前5阶自振频率与有限元结果最大偏差为0.29%，前2阶自振频率偏差为0，计算结果基本吻合。

表3 梁索组合结构体系前5阶自振频率
Tab. 3 First 5th order natural frequencies of the cablebeam structure system

注：=(-)/。

阶数 f1（本文算法）/Hz f2（有限元）/Hz 偏差s/%1 2.58 2.58 0 2 2.93 2.93 0 3 3.49 3.48 0.29 4 4.51 4.50 0.22 5 8.38 8.36 0.24

以式（23）为例，由离散傅里叶原理可知，梁单元位移动力响应由

N

阶频率分量组成，对于移动荷载下的结构响应而言，若高阶频率分量的贡献有限，则可以通过适当的频域窗口选取，以较小的精度损失，获取更高的计算效率。理论模型主梁的1阶自振频率ω=2.58 Hz，采样点数

N

=32 768，截取的最高频率称为截止频率 ω，不截取频率时的最高分析频率为 ω,定义

f

= ω/ω，当

f

分别取值为1、2和10时，计算结果如图9所示。同时，不截取频率 ω=ω时，算法结果也在图9中进行了对比，图9对应的算例模型的梁索夹角 α =45。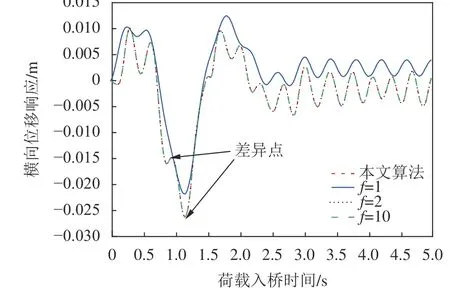

图9 f 不同取值时挠度时程曲线对比Fig. 9 Comparison of deflection time history curves with different values of f

由图9可见：当

f

=1时，计算结果有较大偏差，最大偏差为20%；当

f

=2时，位移曲线与不截取频率时极为接近，在曲线局部峰值位置存在轻微差异。对于算例模型，

f

=2，计算用时仅为无截止频率计算时间的2%。由此可以推论，移动荷载作用下，结构以低频响应分量为主，对于算例梁索组合结构体系，能量主要集中在频率小于2倍1阶自振频率的低频分量，因此，对于MRRM法，可通过截取低频分量，提高计算效率。

4 结 论

本文对MRRM在梁索组合结构中求解弥散波的应用进行了研究，基于DFT思想改进传统MRRM法，使其适用于分析结构中弥散波的传播特性，求解移动荷载作用下结构的瞬时响应，结果如下：

1）本文算法与现场实测得到的跨中动应变波动变化趋势较为接近，应变幅值有一定偏差，计算结果较为合理。试验车辆以速度

V

=30 km/h行驶时，大部分位置的波动趋势的实测曲线与理论曲线吻合较好，当

t

=1.54 s时，即车辆移动到跨中位置时，应变幅值出现偏差为8%；当车辆逐渐接近跨中位置时，实测曲线在个别点处出现实测波峰不明显的情况，如在

t

=1.2 s时，实测应变与理论应变峰值出现最大偏差为22%。当

V

=40 km/h，实测曲线的波动趋势与理论曲线能较好吻合；在车辆逐渐接近跨中位置的过程中，实测应变曲线在少数位置也出现波峰不明显的现象。桥梁附属设施和截面内部的纵向加劲肋均会增大截面刚度，使得实测结果整体略小于理论结果。且在实桥现场测试过程中，干扰因素较多，实测结果不可避免会有所损失，这也是局部点位处出现实测峰值不明显，造成应变幅值偏差较大的原因，故该计算结果是合理的。有限元结果与本文算法得到的结果较为接近，最大偏差为5%，且相较有限元法，本文算法是基于行波解，避免了离散误差，求解结果更能体现结构响应的波动特性。

2）对于梁索组合体系结构，梁索夹角 α=45°或90°时，本文算法得到的横向位移曲线与有限元结果相比，曲线波动趋势具有较高的吻合度；相比有限元结果，本文算法得到的位移峰值略大，最大偏差为9%，这是因为波在有限元分析中是耗散的，有限元分析表明，本文算法的计算结果合理，理论分析正确。以本文的简化力学模型为例，研究发现在移动冲击荷载下，随着梁索夹角增大，主梁横向位移逐渐减小，即较大的梁索夹角可以增大结构体系的动刚度。

3）通过适当截取频率范围，忽略高阶分量的影响，大大提高了MRRM法的计算效率。研究发现，对于梁索组合结构，截取频率 ω/ω≥2，位移曲线与不截取频率时基本无偏差。且对于该理论模型，ω/ω=2，计算用时仅为无截止频率用时的2%。可得出，移动荷载作用下，梁索组合结构以低频响应为主，本文的力学模型，主梁中的波动能量主要由频率低于2ω的弯曲波携带。