让知识巩固与方法掌握同行
——以“平面图形的认识”的整理与复习为例
2022-05-24江苏灌南县新安镇中心小学222599于小燕
江苏灌南县新安镇中心小学(222599)于小燕
在“平面图形的认识”复习课一开始,教师先点明了课题,引导学生回忆所学过的各种平面图形,然后板书课题——“平面图形的认识”的整理与复习,由此展开本节课的复习教学。
一、从“角”的角度整理归类

生2:能拼出直角三角形和钝角三角形。
师:这就奇怪了,为什么在直角和钝角上加一条线段只能拼出一种三角形,而在锐角上加一条线段却能拼出三种呢?
师生小结:这主要与三角形的内角有关,由于三角形的内角和为180°,于是可以派生出许多推论,如任意一个三角形至少有2个内角是锐角,至多只能有1个内角是直角或者钝角,最大角是什么角,三角形就属于同名同类的一类三角形。
教师板书:三角形的内角和为180°,至少存在2个锐角。
师:如果按照内角的大小来分类,三角形可分为三大类,可以画图表示它们的种属关系(如图1)。

图1
【设计说明:本环节以“在锐角上加一条线段拼成三角形”进行导入,再让学生在直角和钝角上加一条线段拼成三角形,并通过对比,使学生产生“在不同的角上搭建三角形,其形状不一”的认知,然后顺势而为,让学生对三角形进行分类。通过对在不同类型的角上搭建三角形的操作与对比,激发学生的好奇心和探究欲,使学生的思维沿着“回忆—应用—整理”的逻辑轨道顺利发展。】
传统复习课中,教师大多是让学生将学过的知识重新回顾一遍,或者简略地归纳一下,这种复习很难激起学生的学习兴趣,不能起到巩固旧知的作用,甚至还会让学生产生厌烦和抵触情绪,使原本较为稳固的知识结构变得松散。科学的做法是让学生在富有新意的训练中一步步根据需要启用旧知,而且这还不能是一般的简单应用,应该在学生毫不知情、毫无预兆的情况下出示新题、难题,让学生苦苦思索无果后,能猛然想到曾经学过的看似无用的知识才是解决问题的“金钥匙”。唯有如此,学生才会意识到原来不是知识无趣,而是自己没有领会到其中的奥妙。这样,等到问题迎刃而解,学生不仅进行了深度的训练,而且巩固了旧知。
二、从“边”的角度整理归类
1.以边的长短来划分类别
师:刚刚我们从“角”的角度给三角形分类,若要以“边”的长短划分类别,又该如何操作呢?
师(出示图2):哪三条线段可以成功围成一个三角形?请说出围成的三角形的形状,然后反馈交流。

图2
生1:用三条3厘米长的线段可以围成一个标准的等边三角形。
生2:我还能围成一个标准的等腰三角形。
师:如果要围成等腰三角形,需要用到哪几条线段?
生3:“4,4,3”、“3,3,4”和“4,4,6”。
生4:还有“3,3,6”。
生5:“3,3,6”这个不行,因为3+3刚好等于6。三角形的三边长存在着相互制约的关系,它们首尾相连,两两相接,任意两边的长度之和要大于第三边。
生6:如果选用“3,3,4”组合,拼出的就是锐角三角形。
师:你敢肯定吗?
生6:有八成把握,但不能说十拿九稳。
师:根据三角形的三边长度比例,的确可以推测出各个角的类型甚至具体度数,但这是初中的课程。
师:刚才有同学能依据边长推断角的类型,请说说“4,4,6”和“4,4,3”这两种组合围成的三角形在形状上有何区别?
生7:“4,4,6”这种组合下的三角形很低矮,其形状极有可能是钝角三角形。
生8:“4,4,3”这种组合下的三角形就显得高耸,其形状极有可能是锐角三角形。
师:刚才拼出的三角形都是特例,有没有常规的?
生9:“3,4,6”这种组合下的三角形就是一般三角形。
师:能够围成三角形的充要条件是什么?
生10:任意两边之和大于第三边。
师:三角形三边的长度一旦确定了,三角形的形状和大小也就无法改变。正因为如此,所以三角形具有稳定性。谁来举例说明三角形具有稳定性?
在复习三角形三边的关系时,如果直接引出“三角形任意两边之和大于第三边”,那么学生会感到索然无味,不仅如此,即使学生将这句话背诵几百次,或者教师反复演示讲解其中的原理,学生也未必会开悟,即使教师讲述清楚,学生也只是当时明白,时间久了就会淡忘。复习时,需要强烈的信息源和探究动机来刺激学生的神经,这种重新解析不是零基础的,也不是完全的重学,而是带有原来的操作经验和直觉印象,学生在利用已经给定长度的线段拼出三角形时,会自觉唤醒原有经验,密切注意到三边之间的关系,即使事前不能预测,但是,一旦遇到无法拼成三角形的情况,他们通过对比、联想、回忆,马上就会幡然醒悟:原来能否拼成三角形与其三边长度有莫大关系。
2.整合三角形的关系
师:请将按边分类和按角分类统整为一个集合来表示它们的种属关系。
(学生画出两种图案,如图3所示。)
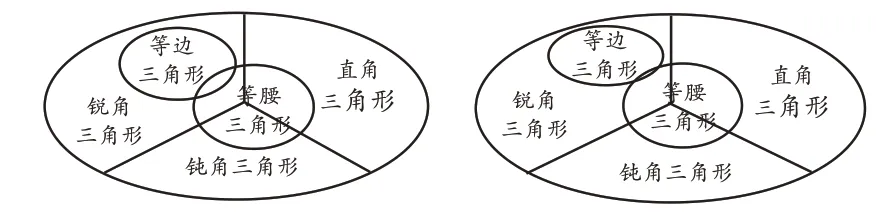
图3
师:这两种图案的共同点是什么?
生1:将等边三角形归置于锐角三角形内,等腰三角形与三种类型的三角形均交叠。(其他学生都表示同意)
师:还有别的不同意见吗?
生2:因为等腰三角形与等边三角形存在交集,也就是有些三角形既是等腰三角形又是等边三角形,所以我赞同第一种。
生3:我反对!等边三角形统统属于等腰三角形。我觉得两个都画错了。
生4:应该把等边三角形完全归置于等腰三角形区域中,同时又要将其完全归置于锐角三角形区域中,因为等边三角形既是等腰三角形又是锐角三角形。(板画出图形,如图4)

图4
师:这样画,等边三角形、等腰三角形、锐角三角形之间的关系全部厘清。看来画对几何图形不容易,要有全局观。
3.整理方法回顾
师:刚才我们是如何一步步整理和复习三角形的知识的?
师:从三角形的角、边入手,系统全面地回顾了它们的特点,理顺它们的种属关系。这也是复习平面图形的一种方法。我们能否用同样的方法来整理四边形?
【设计说明:本环节相当于二次操作,只不过切换了角度,从“边”的角度通过“回忆—应用—整理”来复习三角形的相关知识,并最终与角的分类顺利“汇合”。双线叙事下演绎复习思路,能够让学生在头脑中形成复习“图形与几何”的基本操作模式,即通过对图形的特征研究和辨别来给它们分门别类。值得赞赏的是,两种分类方法本是孤立并存的,本环节将它们熔为一炉,通过“等边三角形的双重属性”打通二者之间的壁垒,让学生在辨析中学会统筹考虑问题。】
复习具有巩固、梳理、整合三大功能,很多教师认为整合就是简单的归整,这是不科学的,如果只是对分散的知识点进行简单的拼组,其内部结构还是松散的。如三角形的分类,可以按角分类,也可以按边分类,如果只是将两种分类方式打包成一个分类主题,那么学生的认知水平并未得到提升。但是,如果将两种分类方式互相渗透,创造出一个新的分类方式,那么不但可以达到对分类这个旧知的整合,而且能够让学生的思维更加缜密,学生对三角形的形状和性质也会有更加全面、深刻、系统的认知。比起简单的知识重组与合并,无论是在广度还是在深度上,这才是卓有成效的复习。
三、独立整理四边形
师:我们已学过的四边形有哪些?回忆其特征,画出分类集合图。
板书:

图5
师:根据集合图回答下列问题。
(1)梯形和平行四边形最明显的不同之处是什么?
(2)“正方形和长方形是特殊的平行四边形”这种论断的理由是什么?
(3)“正方形是特殊的长方形”这种论断的理由又是什么?
师:平行四边形的两组对边分别平行,梯形只有一组对边平行,另一组对边不平行,它们在四边形这个集合中属于特例。
【设计说明:本环节从“边”和“角”两个角度整理复习四边形。学生在独立整理的时候自觉应用前面学过的平面图形基本复习模式,既能复习关于四边形的旧知,又能及时总结复习平面图形的方法。】
四、复习策略总体构想
复习课主要有三大任务:一是对学生的已有知识进行摸底,及时修补漏洞,同时帮助学生梳理所学知识,弄清知识的发展脉络,形成知识体系;二是训练学生的动手操作能力和解题能力;三是进行复习方法指导,教会学生自学、自习。这些任务的完成离不开教师。
第一,复习需要分层落实。本课教学有两大主轴:一是知识层面,将分散的知识点串联起来;二是方法层面,让学生慢慢体验和逐步掌握复习方法。
第二,复习材料需要切合知识本身。教材上的知识点较为分散,时间跨度大,如何在短时间内集中全面地复习?复习材料的选择极为关键。在本课中,选取三角形的“角”和“边”两种分类方式作为基本材料展开复习,并将按角分类和按边分类整合在一起,于是,在自主整理复习四边形时,学生依葫芦画瓢,有模有样。以平面图形的边和角作为典型材料来展开复习,让整节课条理清晰、层次分明,以一个爆发点辐射到整个知识面,提高了复习效率。
第三,复习应重在方法。本节课严格遵照“回忆—应用—整理”的模式展开复习,在授课过程中出示的素材十分开放,学生有很大的自主权,可边复习知识边应用。通过复习,学生的知识得以巩固深化,复习的方法和经验也得到了显著提高。
