促进学生问题提出能力的教学策略研究
——基于情境开放性程度
2022-05-24广东深圳市深圳小学518001王纯旗唐黎明
广东深圳市深圳小学(518001)王纯旗 唐黎明
创设情境是学生提出数学问题的前提条件,有效的情境如同沃土,有助于培养学生发现情境中所蕴藏的关系与规律的能力,激发学生产生认知上的矛盾冲突。本文聚焦“问题提出”教学的情境创设,从情境的开放性程度视角探寻课堂情境创设的教学策略,以期提升学生的问题提出意识与能力。
一、情境开放性程度的内涵与形式
心理学认为情境由“情”和“境”两个维度构成:以‘情’为经,关注学习者的情绪、兴趣等情感因素;以‘境’为纬,关注学习者的实际生活。对于小学教学情境,可以认为是指根据教学内容创设的有情之境,具有三个特点:一是教师干预,是教师基于教学需要而创设的;二是满足学生身心发展需要;三是典型环境。而情境的开放性程度是指情境的结构化程度,主要受到“教师干预”程度的影响,“教师干预”程度越大,那么情境结构化程度越高,情境的开放性程度就越低,反之则情境的开放性程度越高。
本文在借鉴斯托亚(Stoyanova)和艾勒顿(Ellerton)的情境开放性程度划分方法的基础上,将“问题提出”情境的开放性程度分为三类:第一,开放性情境,指既定的、人为的、开放的情境,该情境仅呈现与数学相关的大背景,学生可以基于大背景提出数学问题;第二,半结构化情境,是指开放的和具有一定结构的情境,学生需在探究一定情境结构的基础上,根据情境所提供的结构信息提出问题;第三,结构化情境,是指特定的、结构化程度高的情境,学生需要先研究情境结构,然后根据结构信息提出数学问题。
二、不同开放程度情境的应用策略
1.巧用开放性情境,激发学生提问兴趣
通过研究发现,学生在不同开放程度情境中的数学问题提出能力表现有所差异,在开放性情境中表现最好,其次是半结构化情境,而在结构化情境中表现最差。张丹和吴正宪也对开放性情境进行了研究,发现学生在开放的现实情境下具有提出发展性问题(需要某种程度的认知努力,选择甚至创造解决问题的方法和策略的问题)的潜能,说明在开放性情境中学生的数学问题提出能力表现较好,主要原因为开放性情境为学生提供了开放的情境主题内容,学生所提的数学问题仅需与该主题内容相关,受情境结构的影响非常小,学生能够多方面、多角度地提出数学问题。
因此,在“问题提出”教学初期可以多为学生创设开放性情境,以帮助学生更容易、更多样化地提出数学问题,激发学生提出数学问题的兴趣,为后期的“问题提出”教学打好基础。例如,北师大版教材二年级下册第六单元编排了如图1所示的情境。考虑到二年级学生数学知识储备较少与问题提出经验缺乏,笔者让学生在生生、师生、家生交流后提出数学问题。通过表1可知学生在本单元中想要了解与探究的数学问题,发现学生所提的问题不仅提问视角多样,而且问题符合单元目标要求,有的问题还高于单元目标要求。

表1 在“克与千克”单元中学生所提的数学问题

图1 开放性情境
教师先对学生所提的问题进行了收集,接着组织学生选择1或2个自己想要研究的问题后通过独立完成、家长协助、同伴合作等方式加以解决,并填写学习单(见表2),最后组织学生分享研究成果。
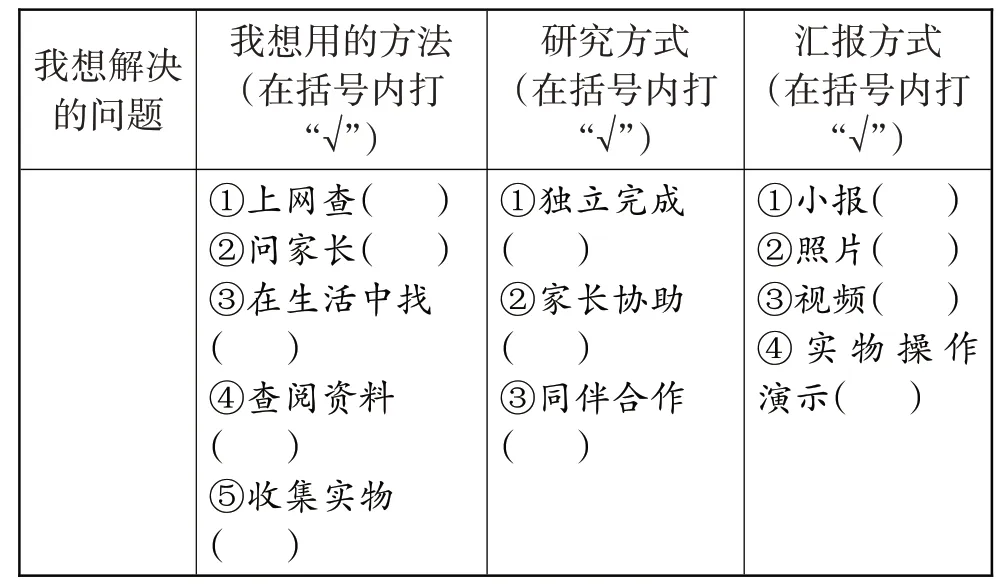
表2 “克与千克”单元学习单
该“问题提出”教学的情境创设案例,充分发挥了开放性情境结构化程度极低的优势,引导学生基于“克与千克”的数学背景,最大限度地提出数学问题。在创设开放性情境时,教师应遵循以下原则:第一,情境要符合教学目标的要求。因为培养学生发现和提出问题意识与能力的目标指向学生的数学知识的学习与数学素养的发展;第二,情境的结构化程度要低,通过数学背景引发学生提问。在“问题提出”教学后期,也可以灵活应用开放性情境,以提升学生所提问题在独创性维度(考查学生所提问题的新颖性)的表现,以更好地发展学生的创造力。
2.活用半结构化情境,培养学生提问意识
研究表明,在半结构化情境中学生的数学问题提出能力表现一般。这说明学生在半结构化情境中不能多方面、多角度地提出数学问题。出现该现象主要与半结构化情境的特点相关,学生需在探究一定情境结构的基础上才能提出数学问题,这在一定程度上限制了学生提问的角度,不利于学生发散思维,增加了提问的难度。
因此,半结构化情境适合在“问题提出”教学中后期或小学中高年级使用,以全面培养学生的数学问题意识,发展学生的数学素养。例如,在五年级“正方体的展开图”的教学中,教师首先展示一个正方体,引导学生想象该正方体的展开图并在学习单上绘制;然后教师展示典型的学生作品(如图2),鼓励学生基于这些作品提出2个及以上的想研究的数学问题,并记录下来(见表3);最后,教师将学生所提问题的难度进行划分,带领学生由易到难循序渐进地解决这些问题。

图2 学生绘制的正方体展开图

表3 在“正方体的展开图”教学中学生所提的数学问题
由上可知,在创设半结构化情境时,教师应遵循以下原则:第一,情境要符合教学目标的要求;第二,要充分发挥该类情境“具有一定结构性”的特点,虽然该特点在一定程度上限制了学生提问的角度,但也为学生提供了更多的数学素材,有助于学生借助这些信息更清晰地提出数学问题;第三,要充分考虑学生数学问题提出能力的差异,以此为出发点设置该类情境的难度。
3.善用结构化情境,提升学生提问水平
在结构化情境中,学生的数学问题提出能力表现较差。这说明学生在结构化情境中很难多方面、多角度地提出数学问题,原因是结构化情境“结构化程度较高”,大大限制了学生提问的空间与角度,加大了学生提问的难度。
因此,结构化情境适合在“问题提出”教学的中后期或小学高年级使用,以更好地提升学生数学问题提问水平。例如,教学六年级的“牛吃草”问题时,可创设图3所示的情境,引导学生从“牛吃草”情境中提取出相关的数学问题,如绳子的长度、牛棚底面边长等,在此基础上鼓励学生结合已学数学知识提出符合问题情境的数学问题。学生能从绳子长度、牛棚大小、牛可以吃到的草的面积,以及这三者间的关系等角度出发,提出许多有研究价值的数学问题(见表4)。最后,教师引导学生将这些问题进行挑选与分类,并以生生合作的方式解决这些问题。
图3 “牛吃草”情境

表4 “牛吃草”情境中学生所提的数学问题
由上可知,在创设结构化情境时,教师应遵循以下原则:第一,要基于教学目标创设结构化情境,使情境真正为学生的学习服务,发展学生的数学素养;第二,要充分发挥该类情境“结构性程度较高”的特点,虽然这大大限制了学生提问的空间与角度,加大了提问的难度,但已有的情境结构信息有助于学生更清晰地提出数学问题,对全面、综合地培养高年级学生数学问题提出能力有着重要的价值。
三、建议
1.基于不同开放程度情境特点培养问题提出能力
学生在不同开放程度情境中的数学问题提出能力表现有显著差异。因此,教师应充分考虑不同开放程度情境的优势与弊端,在此基础上创设情境,更好地引导与帮助学生多方面、多角度地提出数学问题,以培养学生的数学问题提出能力。
2.为学生创造良好的条件以促其更好地提出数学问题
大多数学生具有较强的问题意识,愿意尝试提出问题,但在学生所提的问题中有很多是不正确的数学问题(包括一般陈述问题、非数学问题、不满足题意要求的问题、表达不清晰的问题、不可解的问题),很多学生是为了提问题而提问题。因此,教师应进一步提升学生提出正确数学问题的能力,尤其是提出真问题(真实存在的问题)的能力。这就需要教师为学生提供更多的机会,传授学生一定的问题提出的方法和策略,并营造良好的问题提出氛围,引导学生领悟数学问题提出的价值和趣味,这样学生才能获得积极的情感体验,从而更好地提出数学问题,尤其是提出更多、更好的真问题。
