基于卷积神经网络的矿井提升机制动系统故障诊断方法
2022-05-24李娟莉闫方元梁思羽
李娟莉,闫方元,梁思羽,李 博,苗 栋
(太原理工大学 a.机械与运载工程学院,b.煤矿综采装备山西省重点实验室,太原 030024)
矿井提升机是煤矿能源开采过程中连接井上与井下的关键设备,其能否安全可靠地运行直接关系到煤矿企业的经济效益和生产人员的生命安全。提升机工作环境和结构的复杂性,其性能会随着设备的运行而不断恶化,导致故障发生。作为提升机的重要组成部分,制动系统性能的优劣直接关系到提升机运行的安全性和可靠性。因此借助先进的传感器技术、信号处理技术和故障诊断技术监测设备异常的部位和原因,对潜在故障进行精准的预报和诊断对保证设备的安全运行具有重要意义[1-5]。
机器学习作为一种数据处理算法,在数据的基础上研究故障特征,对故障进行诊断。有的学者提出了基于决策树的故障诊断模型,在处理不同故障类型时具有较高的精度[6-7]。李娟莉等[8]基于贝叶斯理论对矿井提升机故障进行了不确定性推理,得到了较好的故障识别效果。董磊等[9]分析了提升机故障数据的特点,提出了基于复杂网络聚类的故障诊断方法,引入广义Ward距离,能较准确对已知故障数据进行分类。黄秋勇[10]改进了BP神经网络,加入了遗传算法,用于提升机制动系统的故障诊断中,优化后的BP神经网络有更好的收敛速度和诊断准确率。随着传感和监测技术的不断完善,以及测点的增多和采样频率的提高,监测数据出现了数据量大、数据维数多等数据特点,机器学习算法建模复杂,不能充分利用监测数据,很难满足大数据的需要。
机器学习算法将问题拆分成不同的部分,分别对其进行求解,与之相比深度学习则以集中方式解决问题,而不必进行问题拆分,从原始数据中自动挖掘诊断信息,自适应确定模型结构参数。常用的深度学习算法有深度置信网络、卷积神经网络、自动编码器和循环神经网络。INCE et al[11]利用卷积神经网络对电机故障进行了诊断,将特征提取和故障分类融合在一起,证明了方法的有效性。胡茑庆等[12]以行星齿轮箱作为研究对象,通过对振动信号的经验模态分解结合卷积神经网络进行故障分类,准确有效地实现了行星齿轮箱的故障诊断。陈淑梅,朱丹宸等学者指出,故障诊断过程中采集的过程信号通过映射关系转化为图像信号输入卷积神经网络能够提高故障诊断的精度[13-14]。
上述研究成果表明,深度学习在故障诊断方面具有较大的优势,但在提升机上的应用较少,本文充分利用提升机运行中出现的大量监测数据,从监测数据中挖掘提升机的故障信息,建立基于CNN的故障诊断模型,对CNN诊断模型进行优化,使用测试数据集对诊断模型进行试验验证。
1 故障诊断整体框架
本文所研究的内容如图1所示,主要涉及数据采集、数据处理、模型训练以及模型应用四个部分。
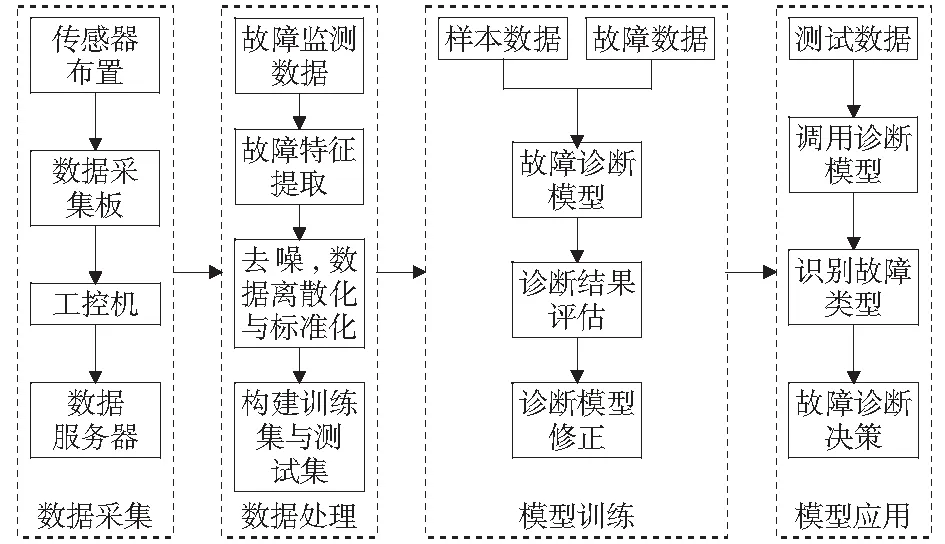
图1 故障诊断框架Fig.1 Fault diagnosis framework
1) 数据采集。数据的来源主要是监测系统对提升机制动系统运行状态实时监测得到的数据与制动系统的历史库中的数据。
2) 数据处理。对采集到的提升机制动系统故障数据和正常运行数据进行冗余、缺失和标准化处理,提取故障特征,并对数据进行去噪、计算特征量处理,构建故障诊断数据集。
3) 模型训练。建立基于CNN的提升机制动系统故障诊断模型,使用训练数据集对诊断模型进行训练,通过对故障诊断结果进行评估,不断修正诊断模型参数。
4) 模型应用。使用测试数据集导入到训练完成的诊断模型中,通过对数据进行分类判断制动系统状态和故障类型。
2 故障机理分析与数据采集
2.1 故障机理分析
矿井提升机的制动系统包括执行机构和传动机构,传动机构是液压站,用以调节和控制制动力矩的大小;执行机构是制动盘,制动盘合闸时的制动力由若干组碟形弹簧提供,在松闸时,液压站将油注入油缸,油压与弹簧力抵消,进而实现松闸。由于提升机结构复杂,加上重载、强振的工作环境,容易导致制动系统发生故障,常见的故障主要包括以下几种:
1) 制动力矩失效,其包括制动力矩过小和制动力矩过大。在制动系统中,制动力矩是一个重要的参数,制动力矩过小会使减速度过小,导致制动位移过大,造成过卷的现象;制动力矩过大引起罐笼停不在预定位置,过大的减速度会使钢丝绳承受的载荷过大,导致钢丝绳的断裂。制动力矩Mz的表达式为:
Mz=2μFNRmn.
(1)
式中:μ为闸瓦对制动盘的摩擦系数,FN为制动正压力,Rm为制动盘平均摩擦半径,n为提升机制动盘副数。若闸盘偏摆超过一定范围,会造成闸瓦位移不一致,使得制动正压力波动剧烈,影响制动效果。引起制动力矩失效的原因主要包括摩擦系数、制动正压力、闸盘偏摆。
2) 残压过高。残压的高低直接影响到制动系统松闸和合闸的速度,进而造成制动失效。造成残压过高的原因主要包括溢流阀的节流孔较大、液压站的调压装置调整不当。
3) 制动油压力过低。制动油压力过低会引起提升机松不开闸,甚至造成闸瓦失效。造成制动油压力过低的原因主要包括油温过高、油液泄漏、油液黏度过高。
4) 闸瓦磨损严重。闸瓦磨损太快,会引起刹车失灵,引起制动失效。引起闸瓦磨损严重的原因主要包括闸瓦间隙过小、闸瓦接触面不平、闸瓦间隙不均匀。
5) 碟形弹簧失效。提升机在制动时,通过碟形弹簧产生的制动力进行制动,碟形弹簧失效会导致制动力不足,进而造成制动失效。在频繁使用后很容易使碟形弹簧的刚度下降,弹簧产生的制动力较小或不产生制动力,使得碟形弹簧失效。
2.2 数据采集
由上述分析可知,闸盘偏摆、闸瓦位移、弹簧力、油压以及闸瓦开合状态是决定制动系统运行状态的重要参数,因此需要对以上参数进行监测和采集。
由于各个参数的数量级和量纲各不相同,如果直接输入到CNN诊断模型,可能会导致诊断模型不收敛,因此需要将监测数据统一到相同尺度下,即标准化。在本文中选用离差标准化,即找出各个监测参数的最值,计算每个监测参数偏离最小值的差占最值之间差的比值,所有的数据经过标准化之后,都在0.04~0.98的范围内。
在运行过程中,传感器的工作环境存在噪声,可能在某个采集周期内,会导致传感器采不到数据或是一次采到多个数据。因此需要对采集来的数据做去冗余和去缺失的处理,由于传感器的采样周期较短,获取的数据量较大,可以直接删除数据缺失的记录。经过去冗余和去缺失后,构成原始数据集。
3 基于CNN的故障诊断模型
3.1 CNN理论分析
CNN是一种具有表征学习能力,仿照生物视觉构建,包含了卷积运算的具有深度结构的前馈型神经网络。本文搭建的CNN诊断模型由卷积层、池化层、全连接层和Softmax层组成,其基本结构如图2所示。

图2 CNN诊断模型结构图Fig.2 CNN diagnosis model structure diagram
卷积层是CNN诊断模型的核心,是提取数据特征的场所。在卷积运算中,感受野依次携带各个卷积核按照一定的步长对输入数据进行扫描,数据与卷积核进行乘法运算后求和,得到与卷积核相对应的运算结果。
池化层是在保证卷积层提取到的特征不被破坏的前提下,按照一定的法则缩减数据的尺寸。在池化运算中,需要将输入的每一层分割成若干个小区域,对于边界上不足以凑成的区域,以0补充,常见的池化运算有平均池化和最大值池化运算。
全连接层相当于一个分类器,它将前面几层得到的数据进行分类,从而输出诊断结果。Softmax层是整个诊断模型的最后一层,其最主要的作用是让输出向量中的每一个分量大的更大,小的更小,且所有分量的和为1,使得输出结果变得更接近期望输出的过程。
3.2 数据编码方法
由于CNN诊断模型是以处理图像见长,因此需将监测数据编码为类似于图像的形式,本质上是将二维数组表示的数据集映射到三维数组表示的数据集上。映射的过程如下:
(2)
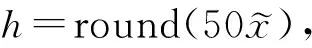

(3)
由此可以求出d的值为:
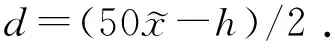
(4)
h=round(50×0.732)=round(36.6)=37,
d=(50×0.732-37)/2=-0.2,
x36=0.25-(-0.2)=0.45,
x37=0.5,
x38=0.25+(-0.2)=0.05,
x其他=0,
X=[0,0,…,0,0.45,0.5,0.05,0,…,0]T.
3.3 算法优化
当神经网络训练数据较少时,可能会出现以下状况:神经网络对训练数据的诊断误差非常小,但是对于未曾参与训练的数据,其误差较大,出现过拟合的现象。由于Dropout的随机性,网络中某些神经元由于训练数据不足而产生的复杂的“共适应”关系将被破坏,由此训练出来的神经网络将更好地面对未知的数据,所以本文在CNN的基础上加入Dropout优化算法。优化算法实现过程如下:
生成与权重和偏置的尺寸大小相同,范围为0~1的随机矩阵R.对矩阵中的每一个元素r作运算l(r),l(r)为线性Dropout函数,其特点是:当随机数r小于丢弃点α时,l(r)=0;当随机数r大于保留点β时,l(r)=1;当随机数r介于两者之间时,将r线性地映射到0~1之间,l(r)的表达式为:
(5)
4 试验验证
4.1 验证过程
本文以实验室2JTP-1.2×1.0P型矿井提升机作为试验设备,对第3节提出的CNN诊断模型进行试验验证,试验设备如图3所示。在制动器上安装NZ891YT型电涡流位移传感器如图4所示,采集闸瓦位移、闸盘偏摆等参数;在液压站的电磁换向阀出口处安装MBS 3050-3415-1GB04型压力传感器如图4(b)所示,监测制动油压的变化;在碟形弹簧底部安装CMKI垫圈式测力传感器,监测弹簧力的变化,传感器安装位置如图4所示。
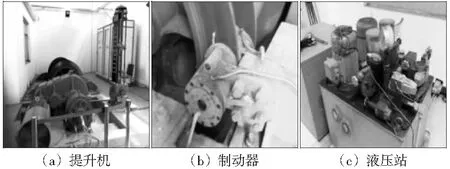
图3 试验设备Fig.3 Test equipment

图4 传感器安装位置Fig.4 Sensor installation location
在对提升机的制动系统进行故障诊断过程中,需要把传感器采集到的数据储存在数据库中,具体采集过程如下:
1) 在提升机关键部位上布置传感器,模拟2.1节中列举的各种故障,具体模拟方法见文献[6],分别采集提升机正常和故障情况下的各类监测数据。
2) 在工控机上利用组态软件对提升机的监测数据进行实时展示,并存储在数据库中。
3) 将采集的数据进行去冗余、标准化以及数据编码后得到用于验证诊断模型的数据集,正常数据和故障数据所占比例为1∶3,其中70%的数据作为训练数据,剩余的数据作为测试数据。采集到的监测数据如表1所示,数据编码后的图像如图5所示。图中表示数据的其中一层,方格颜色越暗,对应的数值越小。
为了检验CNN诊断模型在提升机制动系统故障诊断中的准确性与优势性,本节使用BP诊断模型作为对照组,诊断模型的基本结构参数和迭代次数保持一致,用相同的测试数据集进行对比试验。
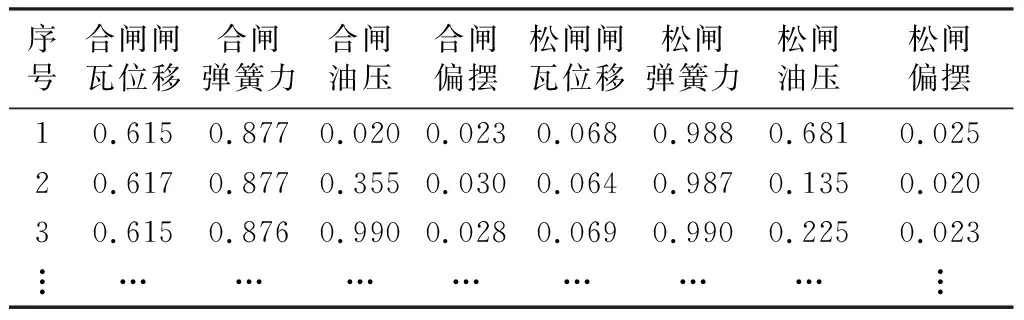
表1 监测数据示例Table 1 Examples of monitoring data

图5 数据编码样本示例Fig.5 Sample test of data encoding
将训练数据集导入到BP和CNN诊断模型,分别迭代更新模型参数,完成诊断模型的训练。将相同的测试数据集分别导入到训练完成的BP和CNN诊断模型,经过正向传播后,比对模型的诊断结果和实际结果是否一致,若一致则记为“正确”,否则记“错误”。统计每类故障的诊断结果,结果如图6所示,其中每个点表示一个数据,“乘号”表示诊断错误,“圆形”表示诊断正确。
4.2 结果分析
通过对比图6的诊断结果可以看出,CNN诊断模型的诊断结果中每一类故障的分布要比BP诊断模型更加紧凑,这说明CNN与BP诊断模型相比,在故障诊断能力和辨识度上具有更高的优势。此外,诊断模型的评价指标包括准确率、召回率等,准确率作为评价诊断模型常用的指标,可以通过比较准确率的大小来衡量模型的优劣性能。分别统计CNN和BP诊断模型在不同数量数据集下的准确率,得到的结果如表2所示。
从表2中可以看出,BP诊断模型对提升机制动系统故障的诊断准确性不如CNN高。随着数据集数量的增加,BP和CNN诊断模型的准确率呈现递增的趋势,当数据集的数量达到2000时,BP诊断模型的准确率达到了81%,CNN诊断模型的准确率保持在98%以上。
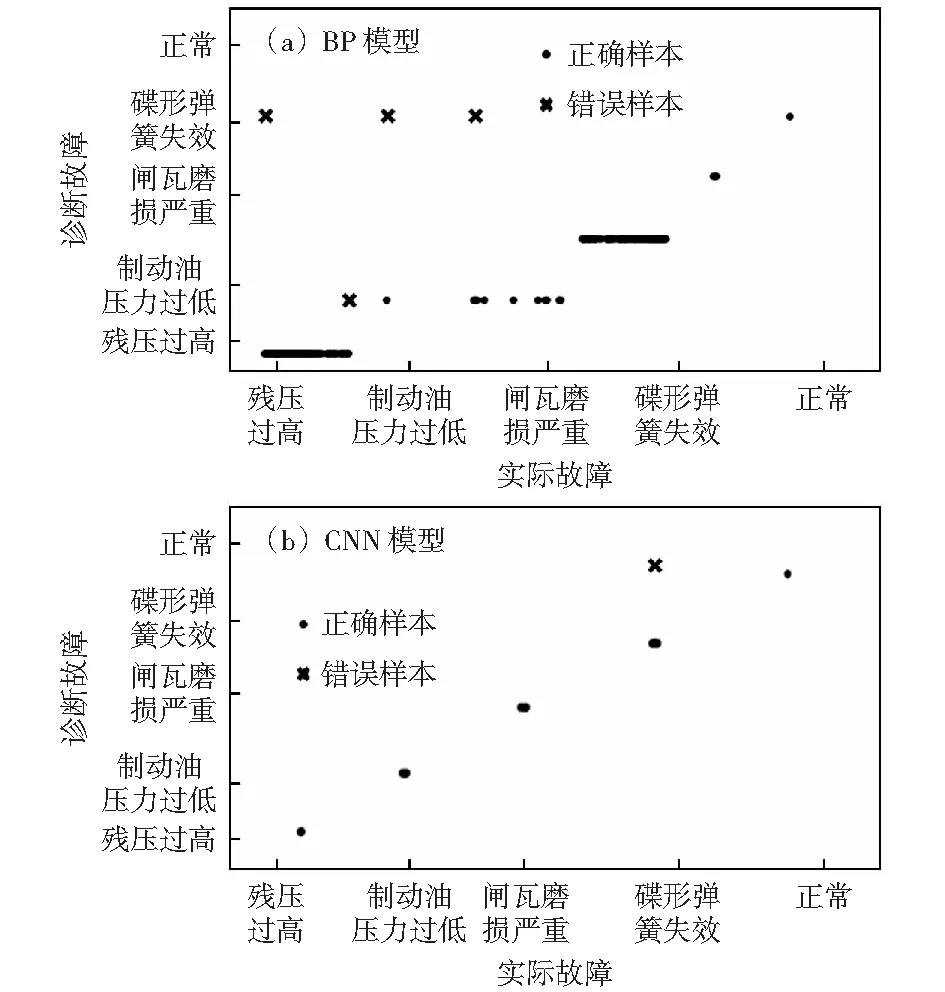
图6 BP和CNN模型的诊断结果Fig.6 Diagnosis result of BP and CNN model
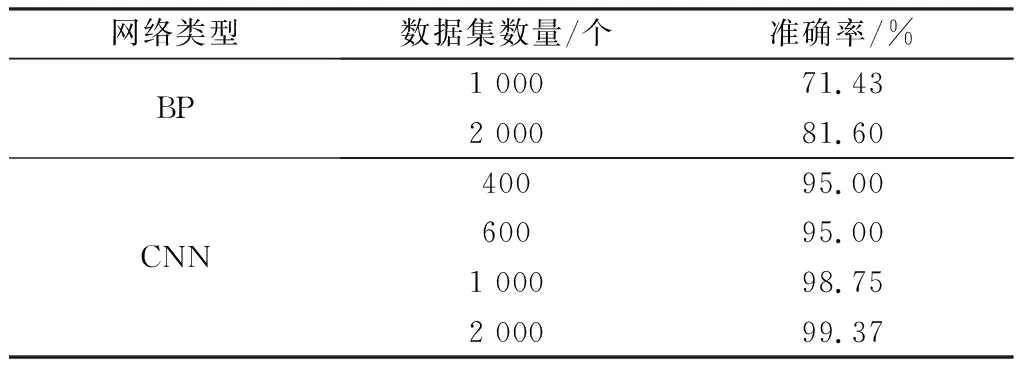
表2 故障诊断准确率Table 2 Accuracy of fault diagnosis
以闸瓦磨损严重的故障种类为例,对模型进行正确性分析。当闸瓦磨损严重时,合闸的闸瓦位移出现明显的增加,合闸弹簧力出现明显的下降,正常状态和闸瓦磨损严重状态下的合闸闸瓦位移和弹簧力如图7所示。
将故障种类为闸瓦磨损严重的故障数据和正常数据导入到CNN诊断模型中,得到的诊断结果如图8所示。图中的蓝色区域表示CNN诊断模型认定的正常数据,红色区域表示CNN诊断模型认定为闸瓦磨损严重的故障数据。从图8中可以看出,CNN诊断模型将测试数据划分为两部分,与制动系统的故障机理一致,表明所提出的CNN诊断模型具有一定的可信度和正确性。
5 结论
本文搭建了一种基于CNN的提升机制动系统故障诊断模型,并对其进行优化。优化后的CNN诊断模型,可以达到98%以上的准确率,与BP诊断模型进行比较,具有较好的准确性。结合制动系统的故障机理,说明了CNN诊断模型的理论正确性。为了充分发挥CNN诊断模型在图像识别中的优势和特点,提出了一种数据编码方法,可以将传感器采集的数字信号转化成图像信号,并将其作为诊断模型的训练和测试数据集。
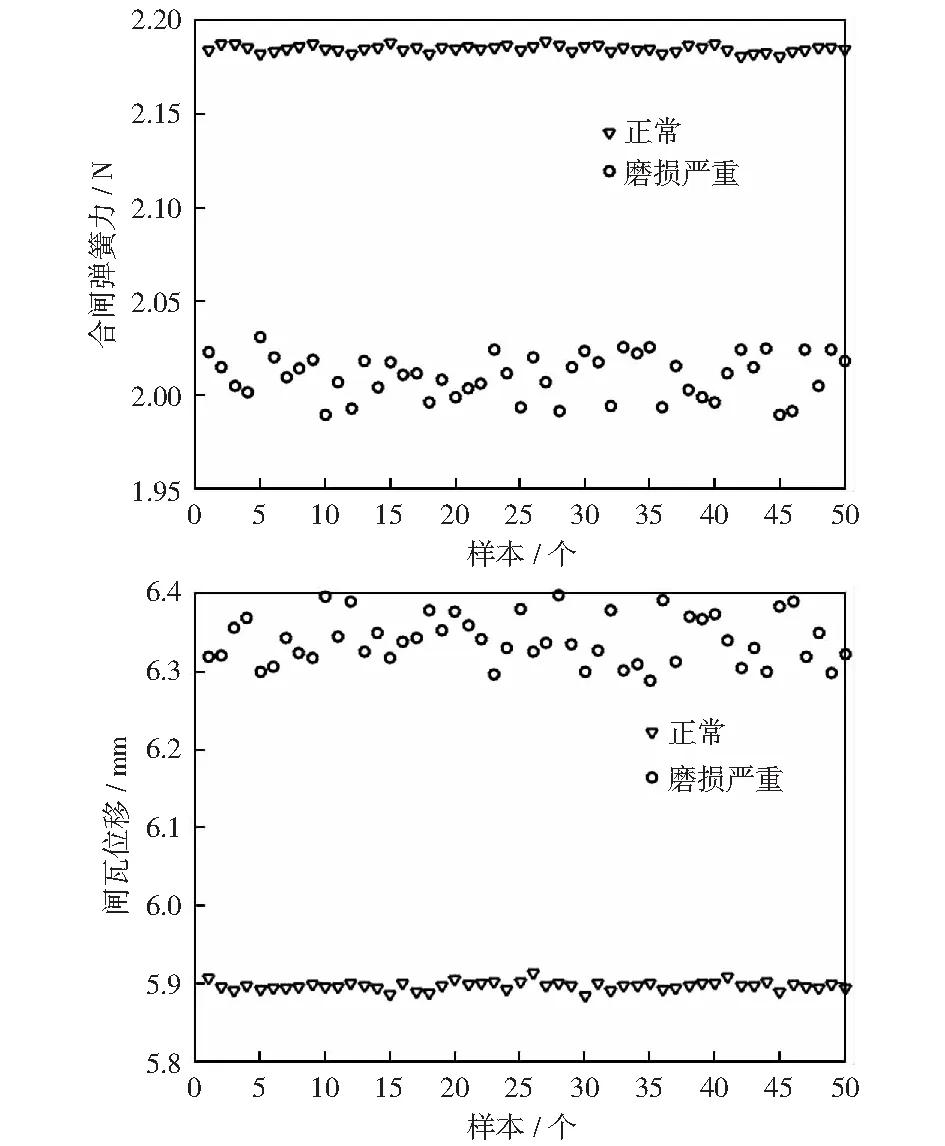
图7 正常与闸瓦磨损严重状态的参数对比图Fig.7 Parameter comparison of normal condition and worn-out brake shoe
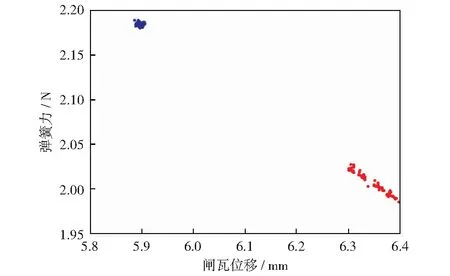
图8 CNN理论正确性检验结果Fig.8 Test result of CNN theory correctness
