海面漂浮弱小电磁辐射源目标定向定位技术
2022-05-24陈清浪庄若望阮开智
陈清浪,庄若望,阮开智
(1.杭州应用声学研究所,浙江杭州 310023;2.上海机电工程研究所,上海 200003)
0 引言
传统的多层次协同定位采用两级定位方法,在此模式下对目标进行高精度定位时,目标定位系统要对目标的实现参数先进行评估,如波达方向(direction of arrival,DOA)、到达时间差(time difference of arrival,TDOA)等。但是在信噪比较低的情况下,参数的估计可能会导致很大的误差,也可能导致错误估计。如果该估计数与其他台站的估计数一起用于定位,对定位结果会有很大影响,有时甚至会导致故障。因此,采用两级定位方法会使目标定位过程中的分辨能力和定位精度受到限制,其主要因素是测向与定位参数融合程度较高,最初的目标参数估计引起了目标信息层面的缺失,给接下来的目标位置参数的估计带来了较大误差。如何在目标参数这一层面有效解决目标信息缺失的弊端,进而主动提高定位算法的定位性能,提高目标测向定位系统定位的精度,是亟待发展和提高的一个关键技术问题。
本文为了避免两级定位方法的处理过程中目标参数估计引起目标信息层面缺失的问题,采用了目标位置参数直接定位(direct position determination,DPD)方法。直接定位方法也叫做目标参数直接估计方法,其最基本的思想是直接从原始数字采样信号中直接估计出目标的位置参数,而不需要额外估计其他的测量参数。DPD 算法主要解决了低噪声比较中目标位置的估计问题和多目标分布的不确定性。该算法保存和使用较低级别的目标信息,在数据融合之后,比传统算法具有更高的定位精度和更强的稳定性。在多目标的情况下,DPD算法不需要参数集匹配,降低了系统复杂度,提高了实时定位精度。
1 多重天线阵列时域参数DPD算法
1.1 算法模型


式(4)可以用来确定接收信号和辐射源之间的位置。则多天线阵列直接联合定位系统的技术问题可被视为:利用采样信号矩阵z,估计被测信号源的位置。为理解以上直接定位的技术问题,需要前提条件如下:
A1:各阵列上的噪声彼此独立,噪声和信号统计也相互独立,接收噪声矩阵w的协方差矩阵匹配零平均复高斯分布,每个阵列的接收噪声相等,从而可得
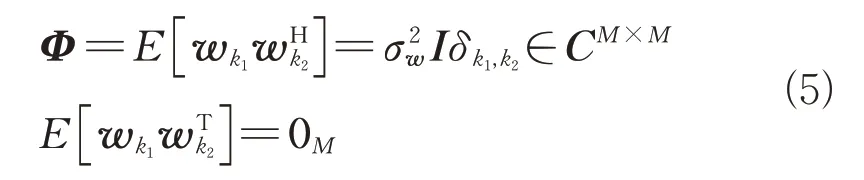

A2:s是需要估计的信号数据模型,接收信号z特征符合正态分布。
A3:辐射源个数已知。
1.2 直接定位算法
确定信号在其波形未知的采样信号序列假设前提下,第个天线阵列信号模型可表达为(=1,…,),令

则式(4)可以写成
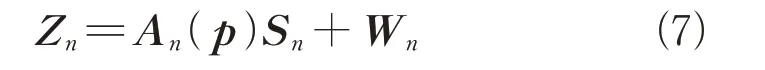
Z的输出协方差矩阵为

一般地,R可估计为
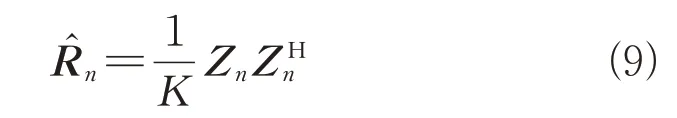



2)最大似然形式
采用时域数据DPD 算法的最大似然估计方法最小化下列方程式:

在固定其他参数的情况下,s的最大似然估计为

由式(12)可得目标位置的最大似然估计为

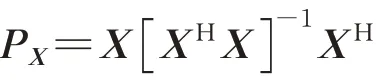
由此可得时域采样数据的最大似然DPD(MLDPD)方法的惩罚函数为
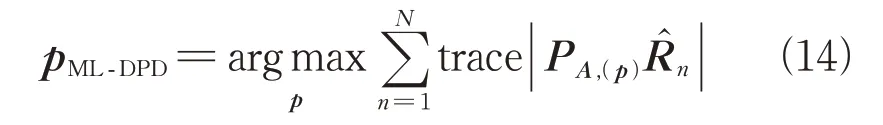
该方法是对时域采样信号最大似然估计,能够获得比SDF-DPD 定位方法更高的定位精度,当信号的信噪比较高时其性能是接近克拉美罗界的。然而当该算法存在多目标条件时,估计方法需要在多维信号子空间中进行估计计算,计算量会明显增大。
1.3 定位误差的克拉美罗界
时域采样数据DPD 算法的克拉美罗界推导过程如下。
需要估计的目标参数为

位误差的克拉美罗下限由Fisher信息矩阵的逆矩阵给出,有
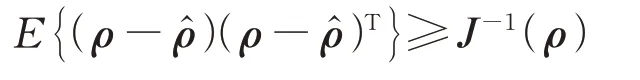
式中:


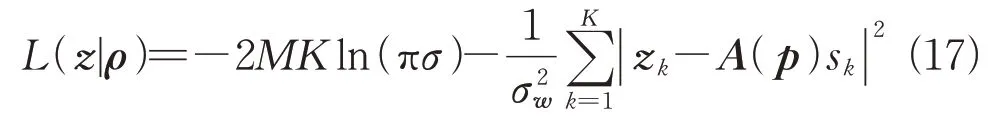
可得时域数据多阵列DPD算法的克拉美罗界:

式中:

2 位置参数估计算法
本文DPD 算法的位置参数估计过程是非线性的目标优化问题,在实际的参数估计过程中需要利用智能优化的算法来求解。比较典型的几类优化算法是网格搜索算法、基于量子粒子群的优化算法(QPSO)以及基于粒子群的优化算法(PSO)等。基于网格搜索的方法是不需要对参数进行初始化的,算法鲁棒性强,但计算量很大。PSO 算法的计算相对简单,且控制参数少,较容易实现,但全局收敛速度无法保证。而QPSO 算法仅需收缩-扩张系数这1 个控制参数,具有更强的全局搜索能力和更快的收敛速度。因此,利用QPSO 算法是去求解直接定位目标参数的优化过程,计算量相对较低。
QPSO的迭代方程组为

式中:(=1,2,…,)表示QPSO算法的第个搜索粒子,为搜索粒子的总数;(=1,2,...,)表示搜索粒子第个维度,为QPSO算法搜索空间维度;为进化代数;u()和φ()均为[0,1]区间上均匀分布的随机数;x()表示进化代数为时在第维的位置,其经历过的最佳位置用p()表示,p()为吸引子位置;G()表示最佳位置;()表示最佳平均位置,定义为所有粒子个体最佳位置的平均值;为比例因子。
3 仿真结果
首先考虑单个干扰源的简单场景。假设个检测台接收信号,各检测台的阵列天线阵列数为。令干扰源的位置坐标为=(,),第阵列的观测信号模型

式中:r()为×1 的实际导向矢量;b为未知估计参数,表示信号源到第个天线阵列复信道函数的衰落因子;a()表示第个天线阵列对位置的干扰源的阵列响应;(-τ())为信号的波形,时延为τ();n()表示观测到的噪声。对每段采样数据进行傅里叶变换,可得
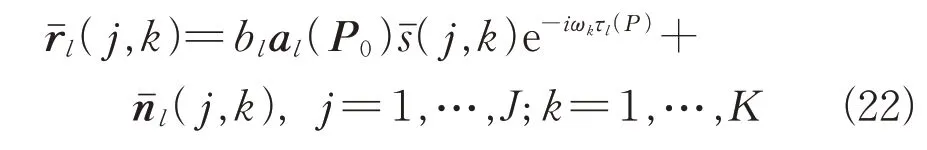
由此可以看出观测信号暗示干扰源的位置信息。首先,阵列响应a()与位置有关,当干扰在远场时,a()是波达角函数。另外,时延τ()也与有关,表示信号源与测量矩阵间的对应关系。
上述模型可推广至多干扰源的情况。假设干扰源数量为,则

在异步模型条件下,多观测站的信号源接收模型可以表示为

针对上述多干扰接收信号模型,基于最大似然的直接定位算法利用阵列天线波束形成概念,将所有阵列天线输出的信号平均功率之和为最大作为代价函数,直接搜索得到信号源的位置参数估计。基于最优权约束估计的最小方差无失真算法(minimum variance distortionless response,MVDR)保证约束方向上的信号被正确接收,另一个方向上的信号或干扰被完全抑制,参数估计分辨率优于传统的波束形成算法。而基于噪声子空间法的阵列多重信号分类方法能够突破瑞利极限的高分辨率。为了提高直接定位的分辨率,本文还将研究基于阵列多重信号分类的多目标高分辨直接定位算法。
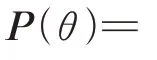

式中:U为噪声子空间矩阵,由R的(-)个最小特征值的特征矢量构成。因此,异步的阵列多重信号分类直接定位方法目标函数为

从上述算法流程可见,与测向交会算法相比,异步子空间融合直接定位算法有效避免了多干扰源交叉定位点配对模糊问题,且避免了二次参数估计的误差传播,能够有效提升低干噪比条件下的定位性能。另外,与同步观测直接定位算法相比,该方法避免了相参处理对同步的严苛要求,并且仅需将协方差矩阵的信息传递至融合中心,避免了同步观测直接定位算法对传输大量原始采样数据的数传压力。
图3给出了飞机在飞行情况下的直接定位谱,2个干扰源坐标分别为[35 km,-4 km],[35 km,4 km],搜索的范围为12 km×10 km 的探测区域,干噪比为12 dB。图3(a)为CBF(conventional beam forming)直接定位方法,(b)为MVDR 方法,(c)为阵列多重信号分类方法,可以看出CBF 直接定位方法依然无法分辨出两个目标,而MVDR和阵列多重信号分类方法都能分辨出。
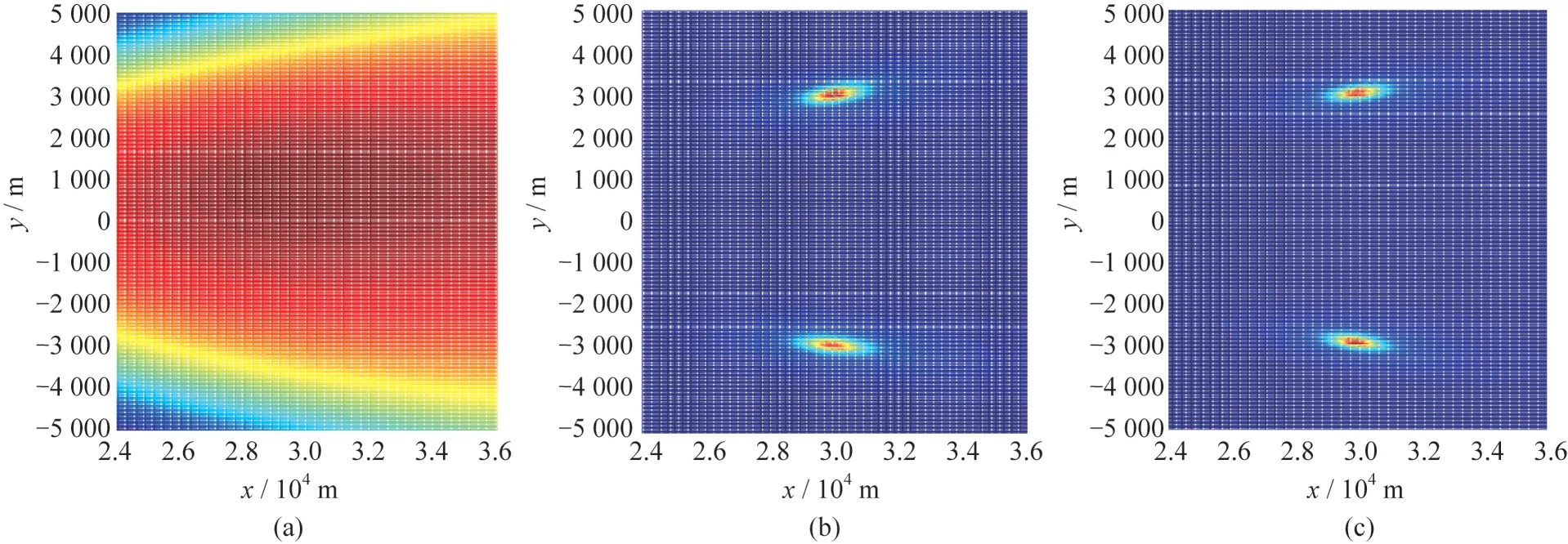
图3 不同方法阵元直接定位谱Fig.3 Comparison of direct positioning spectra of array elements with different methods
为了确定CBF 直接定位的精度、降低计算量,避免仅使用MVDR 与阵列多重信号分类直接定位算法的局限性,本文还进行了以下更深入的直接定位仿真分析。

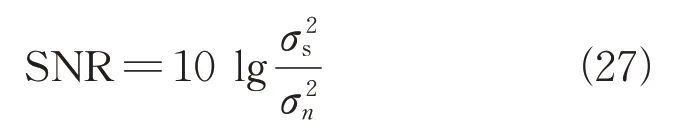
仿真分为5 组,每组计算的蒙特卡罗次数是500次。用目标位置参数估计均方误差(root mean square error,RMSE)来衡量算法的位置分辨率,RMSE 的统计如下:


仿真结果如图4~8所示。
图4 是使用CBF 直接定位算法对干扰源进行定位的结果,从图中可以看出,采用直接定位方法能够准确定位出干扰源。图5~6 验证了定位精度随信噪比的变化情况,可知在低信噪比情况下,基于子空间的干扰源高分辨直接定位仍然能有较高的定位精度,且随着信噪比的增加,其定位精度逐渐提高。

图4 CBF直接定位算法定位结果Fig.4 Location results of CBF direct positioning algorithm

图5 测向快速交叉定位精度随信噪比变化情况Fig.5 Variation of DF fast cross positioning accuracy with signal-to-noise ratio
最后,对测向快速交叉定位与基于子空间的干扰源高分辨直接定位的定位精度进行了仿真比较。图7~8 表明,在低信噪比情况下基于子空间的干扰源高分辨直接定位仍然能有较高的定位精度,其RMSE 明显比基于测向交叉定位的RMSE 要低;但在较高信噪比情况下,测向快速交叉定位与基于子空间融合的直接定位,相比两级定位方法都具有比较高的定位精度,信噪比相同情况下,定位精度可提高25 m。

图6 基于子空间的直接定位精度随信噪比变化情况Fig.6 Variation of subspace-based direct positioning accuracy with signal-to-noise ratio

图7 AOA算法定位精度随信噪比变化情况Fig.7 Variation of AOA positioning accuracy with signalto-noise ratio

图8 DPD算法定位精度随信噪比变化情况Fig.8 Variation of DPD positioning accuracy with signalto-noise ratio
DPD 算法的提出主要是为了解决在低信噪比下目标位置的估计以及多目标的配对模糊问题。由于保留和利用了更多的低层次目标信息,在数据融合之后,低信噪比下该算法可取得比传统算法更好的定位精度及更高的稳定性。在多目标的情况下,DPD 算法不需要对参数集进行目标匹配,降低了系统的复杂度,提高了定位的实时性。
4 结束语
海面漂浮弱小电磁辐射源目标定向定位技术主要通过机载平台应用于浮标搜寻和定位,该系统仅需被动接收VHF频段浮标发射的电磁信号,利用阵列天线高精度测向技术计算出浮标准确方位,利用机载平台位置信息计算出辐射源准确位置。该技术主要有扫频模式和跳频模式,扫频模式主要应用于定位未知辐射源,跳频模式主要应用于定位搜救及已知辐射源。相比于直接定位方法,该方法可以有效地避免数据关联问题,从原始信号数据域中提取目标位置参数,便于直接使用特定波信号。通过仿真可知,直接定位方法可进一步提高定位精度。本文对海面漂浮弱小电磁辐射源目标的定向定位技术研究,可有效进行快速准确的定向定位,是遏制声呐浮标及波浪艇等探测设备的有效手段之一,可以应用到航空电子侦察领域,提升我国领海安全。
