浅谈如何让数学课堂走向深度教学

刘金花

【摘  要】小学六年级的数学教学含有大量的复习课，而在双减背景下，教师要提高课堂效率，必须采用相应的教学策略，引导学生进行深入思考、对比延伸、归纳整理，从而让“教”更有层次、“学”更有深度。

【关键词】深度教学;深入思考;对比延伸;归纳整理

小学数学的教学到六年级，就表示即将进入尾声。以苏教版的教学内容为例，六下的第七单元为《总复习》，包含二十几课时的内容。在比较短的时间，进行如此多内容的复习，对每个教师和学生来说都是巨大的挑战。所以在平时的教学中，教师不能就题论题，要带领学生做好延伸拓展、归纳整理。

一、设置不同层级问题，引导学生进行深入思考

以我们的教学经验来看，许多学生在面对一个数学问题时，由于思考得不透彻，导致题目做得不完整，经常少步骤、错单位。有时他们做出答案往往是凭感觉，没有思考出来问题的关键点，思考也没有逻辑顺序。这时教师在给学生独立思考时间之后，还要提出相应的问题引导学生将思维走得更深入。以下面几题为例，简单谈一谈如何让学生做到深入思考。

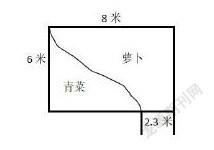
案例1：李大爺在一块长方形地里分别种了萝卜和青菜（如图）。萝卜地的周长和青菜地的周长相比：（     ）

A.萝卜地的周长比青菜地长2.3米

B.萝卜地的周长比青菜地长4.6米

C.萝卜地的周长和青菜地一样长

这是一个关于周长的问题，所以学生第一步要知道萝卜地和青菜地的周长分别是什么。第二步要让学生完整说出自己的想法，思路必须要清楚。最后一步，就是提出其他建议和补充。那么教师可以这样设计问题：①请用不同颜色的笔描出萝卜地和青菜地的周长;②做出判断并写出自己的思路;③你还有其他的想法或者补充吗？

问题①的目的是让学生知道周长在哪里。问题②是鼓励学生用不同的方法来解决问题，比如有的学生会用字母表示数，用a表示曲线的那条边，那么萝卜地的周长就是8+6+2.3+a=16.3+a，青菜地的周长就是8-2.3+6+a=11.7+a。还有的学生会想到先把相同部分去掉，那么萝卜地的周长就剩下（长+2.3），青菜地的周长剩下（长-2.3），这样也能看出它们的差是4.6。问题③是想让学生自己补充发现，比如有的学生会想到什么时候两块地的周长相同，还有的学生会想到题目中其他条件都是多余的，只需要2.3这个条件就能解决问题。

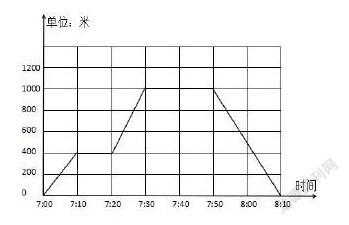
案例2：王宇步行从家去图书馆，根据折线统计图，回答问题：

（1）王宇家距图书馆（     ）米。

（2）王宇去时在400米处遇见同学停留了（   ）分钟。

（3）王宇在图书馆借书用了（   ）分钟。

（4）王宇回去时的速度是每分钟行（     ）米。

这个题目中的四个填空都是比较基础的问题，只要能把统计图看懂，搞清楚路程和时间的关系，要完全答正确并不难。从学生的反馈来看，前三个空正确率挺高，但是第四个空错误率就比较高了。在做问题设计的时候，教师要把握好学生的易错点和难点来考虑。

问题设计：①认真观察统计图，思考图中纵轴、横轴、线段代表的含义，并和同桌交流;②认真填空，并说明理由;③从图中你还能发现什么？在这里问题③的设计，就是希望学生还能探究得更深入一些，比如“7：00—7：10和7：20—7：30的折线都在上升，表示的含义有什么不同之处？”可以看出7：00—7：10这一段，10分钟走了400米;7：20—7：30这一段，10分钟走了1000-400=600米，可见走路速度是提高了的。

二、从已有学习经验出发，引导学生进行对比延伸

到了小学高年级，知识点越来越多，问题的综合程度也越来越高，课堂的教学任务也越来越重，学生的学习程度又参差不齐，所以很多教师觉得巩固基础花费时间应该更多，而延伸探究这类需要时间的活动只能被忽略。但是时间长了，会发现学生只会做见过的题目，没有见过的题目不知道怎样去思考;而且学生更多地重视方法和结果，对程序性的操作原理知之甚少。下面从几个案例入手，谈谈怎样在旧知和新知之间建立联系，找到知识的延伸点。

案例3：在探究梯形面积计算公式时，可以将梯形沿两腰中点的连线剪开，将上面部分旋转后与下面部分拼成一个平行四边形。

平行四边形的底等于梯形的（     ）;平行四边形的高等于梯形的（     ）;

如果梯形的上底是a，下底是b，高是h，平行四边形的面积：底×高，那么梯形的面积：

S=（       ）×（       ） =（        ）

从而根据平行四边形的面积计算公式推导出梯形的面积计算公式。

这是一个关于梯形面积公式的推导过程的问题。梯形的面积公式的推导在五年级学过，借助的是将两个完全相同的梯形拼成一个平行四边形。因为有之前两个完全相同的三角形拼成一个平行四边形的例子，学生就比较容易接受这个方法。所以大部分教师也就没有介绍其他的方法来推导梯形的面积。但是实际上，梯形面积公式的推导方法很多，比如用分割法，将梯形分割成两个三角形，或者将梯形分割成一个平行四边形和一个三角形，都可以推导出梯形的面积公式。

在研究这个问题时，对比延伸是非常重要的，都是要运用转化的策略，但是方法不是唯一的。延伸可以开拓学生的思维，让学生体会到数学并不总是套路，是有灵气在其中的。

案例4：当我看到“球体”的学习课题时，首先我想：什么样的形体是球体？就是我们玩的篮球、足球等，球体和圆柱、圆锥、长方体、正方体一样，它们都应该属于立体图形。其次我想：用什么学习方法进行学习呢？我估计可以用测量、计算、推导、比较等方法学习这些内容。最后我想：学习它的确有用，例如国际乒乓比赛用球的大小规定就与我们的学习有关。

这个题目的出法也比较新颖。有的教师觉得学生没必要知道知识的逻辑顺序，但是笔者觉得同一类问题，我们把握了大致的学习方向之后，学习起来会更省力。比如六下的《圆柱与圆锥》，它们的研究模式和长方体、正方体的研究模式相同，也是先认识特征，再研究表面积，再研究体积，中间穿插各种不同问题的应用。

在本题中，对学生还没有见过的“球体”的研究，当然是希望学生立足于现有的知识基础上，用已有的处理问题的经验来研究新的图形，也就是说，我们同样要去研究球体有什么特征，其次要知道球体的表面积如何求，另外肯定要知道它的体积怎样计算。如果学生在平时的学习中，已经建立了这样的学习模型，这样的问题是很简单的。

三、建立知识网络，引导学生进行归纳整理

随着年级的升高，学生发现想拿到好成绩越来越难，这是因为问题的综合程度越来越高，考查的知识点越来越多，一旦知识点有漏洞，在考查的时候就会出现错误。所以需要对所学过的知识点进行归纳整理，建立完整的知识网络。归纳整理也分很多类，比如对法则的归纳、对策略应用的归纳、对同一种模型的归纳、对类似知识点的归纳等，下面来举几个例子进行说明。

案例5：20-18=2，0.17+3.23=3.4，（    ）。这三道题目计算方法之间的联系是（    ）。

这个题目一出，看懵了很多老师和学生。计算很常见，分门别类地整理整数、小数、分数的计算法则也都带着学生做过，但是这样寻找三种不同运算的联系是第一次见到。对整数运算来说，教学时更侧重于“相同数位相加减”;小数运算的教学更侧重于“小数点对齐”，其实也是为了保证“相同数位相加减”。而分数的运算学生接触得比较晚，它的教学更侧重于“分母相同、分子相加减”，如果遇到异分母分数加减法，则需要通过通分，将异分母分数转化成同分母分数进行运算。

如果这个题目只是考查整数和小数计算方法的共同点，估计很多学生能回答出来。但是加了分数运算之后，答对的学生非常少。其实分数运算，也是经过通分，将每个分数的分数单位转化成相同的，再进行计算。所以，这个地方我们可以填写的是“相同计数单位相加减”。也就是说，平时我们做的归纳整理，不仅要关注一类知识点的梳理，还要在相似的积累知识点之间建立联系。

案例6：下面运用了“转化”思想方法的有（   ）。

①小數乘法的计算;②平行四边形面积的推导;③圆柱体积公式的推导。

A.②

B.①②

C.②③

D.①②③

策略的教学在小学是一个非常重要的内容，从三年级开始，基本上每个学期都有一个单元来专门教学“解决问题的策略”。策略的教学一般可分为三步：产生策略的需要、怎样应用这个策略、什么样的问题可以用这个策略。

“转化”是小学高年级特别指出的一个策略。它的出现其实是为了在新知识和旧知识之间建立联系，培养学生用已知解决未知问题的意识。它的应用也非常广泛，不止题目中举的三个例子，还有比如将异分母分数转化成同分母分数计算，比如圆面积公式的推导。这类策略的长期运用，可以使学生懂得碰到不会、没见过的问题，要从自己学过的知识里去找办法。

案例7：数学小文章：请你以“分数和百分数”为题，写一篇150字左右的数学小文章，把对“分数和百分数”的知识的理解表达出来。（提示：需包含以下要点。1.分数和百分数的意义;2.分数和百分数的联系与区别;3.分数和百分数的应用。）

这是个非常典型的考查学生对知识点掌握程度的问题。概念教学在小学教学的内容中所占的比重也很大，而且每到概念教学的单元，知识点还特别杂、特别多。比如《年、月、日》《因数与倍数》，都是非常庞大的单元。

以这个小文章的内容为例，“百分数”是六年级的教学内容，而分数从三年级就开始接触了。在六年级将过去所学的分数内容进行回顾，并将百分数与分数联系起来，这个意义是非常重大的。从学生的回答来看，学生对分数和百分数的意义表述不准确，由此可知，纯概念性的内容，学生不乐于记忆，但是应该允许学生用自己语言进行归纳。

总之，教师在平时的教学中要有意识锻炼学生深入思考、对比延伸、归纳整理的能力，才能让学生在考试中灵活应对各种问题。